Skip to main content
Springer Nature Link
Log in

Algorithm for T-spherical fuzzy MADM based on associated immediate probability interactive geometric aggregation operators

  • Published:
Artificial Intelligence Review Aims and scope Submit manuscript

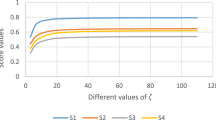
Abstract

The purpose of writing this manuscript is to point out some limitations of existing associated immediate probability intuitionistic fuzzy geometric aggregation operators as these existing operators fail under some conditions such as the existing operators cannot handle the information given in Pythagorean fuzzy sets, picture fuzzy sets, spherical fuzzy sets, and T-spherical fuzzy sets and the existing aggregation operators also cannot aggregate the membership value when membership value of anyone intuitionistic fuzzy number become zero. To overcome these shortcomings associated immediate probability geometric aggregation operators have been developed for T-spherical fuzzy sets and associated immediate probability interactive geometric aggregation operators are proposed. Then a comparison between these operators is developed with the help of an example. The existing score function for T-spherical fuzzy sets does not involve abstinence so a new score function is developed which provides a better comparison between any two T-spherical fuzzy numbers. To demonstrate the presented algorithm, a decision-making process algorithm is presented with T-SFS features. The advantages of the proposed work are also discussed in which it is shown that under some conditions the proposed operators can be reduced to other tools of uncertainty. The comparison between existing and proposed work is also developed with the help of an example.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  • Ashraf S, Mehmood T, Abdullah S, Khan Q (2018) Picture fuzzy linguistic sets and their applications for multi-attribute group. Nucleus 55(2):66–73

    Google Scholar 

  • Atanassov KT (1986) Intuitionistic fuzzy sets. Fuzzy Sets Syst 20:87–96

    Article  Google Scholar 

  • Chen SM, Chang CH (2016) Fuzzy multiattribute decision making based on transformation techniques of intuitionistic fuzzy values and intuitionistic fuzzy geometric averaging operators. Inf Sci 352:133–149

    Article  Google Scholar 

  • Cuong BC (2014) Picture fuzzy sets. J Comput Sci Cybern 30:409–420

    Google Scholar 

  • de Campos ILM, Carmona MJ (1989) Representation of fuzzy measures through probabilities. Fuzzy Sets Syst 31(1):23–36

    Article  MathSciNet  Google Scholar 

  • Garg H (2016a) Generalized intuitionistic fuzzy multiplicative interactive geometric operators and their application to multiple criteria decision making. Int J Mach Learn Cybern 7(6):1075–1092

    Article  Google Scholar 

  • Garg H (2016b) A new generalized Pythagorean fuzzy information aggregation using Einstein operations and its application to decision making. Int J Intell Syst 31(9):886–920

    Article  Google Scholar 

  • Garg H (2016c) A novel correlation coefficients between Pythagorean fuzzy sets and its applications to decision-making processes. Int J Intell Syst 31(12):1234–1252

    Article  Google Scholar 

  • Garg H (2017a) Generalized Pythagorean fuzzy geometric aggregation operators using Einstein t-norm and t-conorm for multicriteria decision-making process. Int J Intell Syst 32(6):597–630

    Article  Google Scholar 

  • Garg H (2017b) Some picture fuzzy aggregation operators and their applications to multicriteria decision-making. Arab J SciEng 42(12):5275–5290

    Article  MathSciNet  Google Scholar 

  • Garg H (2018) Linguistic Pythagorean fuzzy sets and its applications in multiattribute decision-making process. Int J Intell Syst 33(6):1234–1263

    Article  Google Scholar 

  • Garg H, Kumar K (2020) A novel exponential distance and its based TOPSIS method for interval-valued intuitionistic fuzzy sets using connection number of SPA theory. Artif Intell Rev 53(1):595–624

    Article  Google Scholar 

  • Garg H, Munir M, Ullah K, Mahmood T, Jan N (2018) Algorithm for T-spherical fuzzy multi-attribute decision making based on improved interactive aggregation operators. Symmetry 10(12):670

    Article  Google Scholar 

  • Liu P, Chen SM (2016) Group decision making based on Heronian aggregation operators of intuitionistic fuzzy numbers. IEEE Trans Cybern 47(9):2514–2530

    Article  Google Scholar 

  • Liu P, Mahmood T, Khan Q (2017) Multi-attribute decision-making based on prioritized aggregation operator under hesitant intuitionistic fuzzy linguistic environment. Symmetry 9(11):270

    Article  Google Scholar 

  • Liu P, Khan Q, Mahmood T, Hassan N (2019) T-spherical fuzzy power muirhead mean operator based on novel operational laws and their application in multi-attribute group decision making. IEEE Access 7:22613–22632

    Article  Google Scholar 

  • Mahmood T, Ullah K, Ullah M, Jan N, Deli I (2017) Some aggregation operators for bipolar-valued hesitant fuzzy information based on Einstein operational laws. J EngApplSci 36(2):63–72

    Google Scholar 

  • Mahmood T, Ullah K, Khan Q, Jan N (2018a) An approach toward decision-making and medical diagnosis problems using the concept of spherical fuzzy sets. Neural Comput Appl. https://doi.org/10.1007/s00521-018-3521-2

    Article  Google Scholar 

  • Mahmood T, Ullah K, Khan Q (2018b) Some aggregation operators for bipolar-valued hesitant fuzzy information. J FundamApplSci 10(4S):240–245

    Google Scholar 

  • Mahmood T, Liu P, Ye J, Khan Q (2018c) Several hybrid aggregation operators for triangular intuitionistic fuzzy set and their application in multi-criteria decision making. GranulComput 3(2):153–168

    Google Scholar 

  • Pamučar D, Janković A (2020) The application of the hybrid interval rough weighted Power-Heronian operator in multi-criteria decision making. Oper Res EngSci Theory Appl 3(2):54–73

    Google Scholar 

  • Peng X, Selvachandran G (2019) Pythagorean fuzzy set: state of the art and future directions. Artif Intell Rev 52(3):1873–1927

    Article  Google Scholar 

  • Quek SG, Selvachandran G, Munir M, Mahmood T, Ullah K, Son LH, Thong PH, Kumar R, Priyadarshini I (2019) Multi-attribute multi-perception decision-making based on generalized T-spherical fuzzy weighted aggregation operators on neutrosophic sets. Mathematics 7(9):780

    Article  Google Scholar 

  • Sinani F, Erceg Z, Vasiljević M (2020) An evaluation of a third-party logistics provider: the application of the rough Dombi-Hamy mean operator. DecisMakApplManagEng 3(1):92–107

    Google Scholar 

  • Sirbiladze G, Khutsishvili I, Midodashvili B (2018) Associated immediate probability intuitionistic fuzzy aggregations in MCDM. Comput Ind Eng 123:1–8

    Article  Google Scholar 

  • Ullah K, Mahmood T, Ali Z, Jan N (2019) On some distance measures of complex Pythagorean fuzzy sets and their applications in pattern recognition. Complex IntellSyst 6:1–3

    Google Scholar 

  • Wang R, Wang J, Gao H, Wei G (2019) Methods for MADM with picture fuzzy muirhead mean operators and their application for evaluating the financial investment risk. Symmetry 11(1):6

    Article  Google Scholar 

  • Wei G (2017) Pythagorean fuzzy interaction aggregation operators and their application to multiple attribute decision making. J Intell Fuzzy Syst 33(4):2119–2132

    Article  Google Scholar 

  • Wei G (2018) Picture fuzzy Hamacher aggregation operators and their application to multiple attribute decision making. Fundamenta Informaticae 157(3):271–320

    Article  MathSciNet  Google Scholar 

  • Wei GW, Merigó JM (2012) Methods for strategic decision-making problems with immediate probabilities in intuitionistic fuzzy setting. Scientia Iranica 19(6):1936–1946

    Article  Google Scholar 

  • Wei G, Alsaadi FE, Hayat T, Alsaedi A (2018) Projection models for multiple attribute decision making with picture fuzzy information. Int J Mach Learn Cybern 9(4):713–719

    Article  Google Scholar 

  • Wu SJ, Wei GW (2017) Picture uncertain linguistic aggregation operators and their application to multiple attribute decision making. Int J Knowl Based IntellEngSyst 21(4):243–256

    Google Scholar 

  • Xu Z (2010) Choquet integrals of weighted intuitionistic fuzzy information. Inf Sci 180(5):726–736

    Article  MathSciNet  Google Scholar 

  • Xu Z, Yager RR (2006) Some geometric aggregation operators based on intuitionistic fuzzy sets. Int J Gen Syst 35(4):417–433

    Article  MathSciNet  Google Scholar 

  • Yager RR (2013) Pythagorean fuzzy subsets. In: Proceedings of the 2013 Joint IFSA world congress and NAFIPS annual meeting (IFSA/NAFIPS), Edmonton, AB, Canada, 24--28 June 2013

  • Yager RR (2016) Generalized orthopair fuzzy sets. IEEE Trans Fuzzy Syst 25(5):1222–1230

    Article  Google Scholar 

  • Zadeh LA (1965) Fuzzy sets. Inform Control 8:338–353

    Article  Google Scholar 

  • Zeng S, Hussain A, Mahmood T, Irfan Ali M, Ashraf S, Munir M (2019) Covering-based spherical fuzzy rough set model hybrid with TOPSIS for multi-attribute decision-making. Symmetry 11(4):547

    Article  Google Scholar 

  • Zhan J, Sun B (2018) Covering-based intuitionistic fuzzy rough sets and applications in multi-attribute decision-making. ArtifIntell Rev 53:1–31

    Google Scholar 

  • Zhang X, Xu Z (2014) Extension of TOPSIS to multiple criteria decision making with Pythagorean fuzzy sets. Int J Intell Syst 29(12):1061–1078

    Article  Google Scholar 

  • Zhang X, Liu P, Wang Y (2015) Multiple attribute group decision making methods based on intuitionistic fuzzy frank power aggregation operators. J Intell Fuzzy Syst 29(5):2235–2246

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics and Statistics, International Islamic University, Islamabad, Pakistan

    Muhammad Munir, Tahir Mahmood & Azmat Hussain

Authors
  1. Muhammad Munir
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Tahir Mahmood
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Azmat Hussain
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Muhammad Munir.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Munir, M., Mahmood, T. & Hussain, A. Algorithm for T-spherical fuzzy MADM based on associated immediate probability interactive geometric aggregation operators. Artif Intell Rev 54, 6033–6061 (2021). https://doi.org/10.1007/s10462-021-09959-1

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10462-021-09959-1

Keywords