Abstract
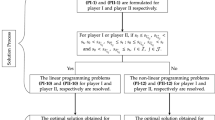
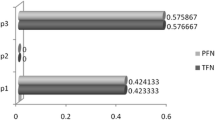
Game theory has found successful applications in different areas to handle competitive situations among different persons or organizations. Several extensions of ordinary game theory have been studied by the researchers to accommodate the uncertainty and vagueness in terms of payoffs and goals. Matrix games with payoffs represented by interval numbers, fuzzy numbers, and intuitionistic fuzzy numbers have considered only the quantitative aspects of the problems. But in many situations, qualitative information plays a crucial role in representing the payoffs of a game problem. This work presents a valuable study on matrix games with payoff represented by linguistic intuitionistic fuzzy numbers (LIFNs). First, the paper defines some new operational-laws for LIFNs based on linguistic scale function (LSF) and studies their properties in detail. Next, we define a new aggregation operator called ‘generalized linguistic intuitionistic fuzzy weighted average (GLIFWA)’operator for aggregating LIFNs. Several properties and special cases of GLIFWA operator are also discussed. The LSF provides an ability to consider the different semantic situations in a single formulation during the aggregation process. Further, the paper introduces some basic results of matrix games with payoffs represented by LIFNs. We develop solution methods using a pair of auxiliary linear/nonlinear-programming models derived from a pair of nonlinear bi-objective programming models. Finally, a real-life numerical example is considered to demonstrate the validity and applicability of the developed methods.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Aggarwal A, Dubey D, Chandra S, Mehra A (2012) Application of Atanassov’s I-fuzzy Set theory to matrix games with fuzzy goals and fuzzy payoffs. Fuzzy Inf Eng 4(4):401–414. https://doi.org/10.1007/s12543-012-0123-z
Aggarwal A, Mehra A, Chandra S (2012) Application of linear programming with I-fuzzy sets to matrix games with I-fuzzy goals. Fuzzy Optim Decis Making 11(4):465–480. https://doi.org/10.1007/s10700-012-9123-z
Arfi B (2006) Linguistic fuzzy-logic game theory. J Conflict Resolut 50(1):28–57. https://doi.org/10.1177/0022002705284708
Atanassov K (1986) Intuitionistic fuzzy sets. Fuzzy Sets Syst 20(1):87–96. https://doi.org/10.1016/S0165-0114(86)80034-3
Atanassov K (1995) Ideas for intuitionistic fuzzy equations, inequalities and optimization. Notes on Intuitionistic Fuzzy Sets 1(1):17–24
Aubin J-P (1981) Cooperative fuzzy games. Math Opera Res 6(1):1–13. https://doi.org/10.2307/3689261
Barron ENEN (2008) Game theory : an introduction. Wiley-Interscience, New Jersy
Bector CR, Chandra S, Vidyottama V (2004) Matrix games with fuzzy goals and fuzzy linear programming duality. Fuzzy Optim Decis Making 3(3):255–269. https://doi.org/10.1023/B:FODM.0000036866.18909.f1
Bector CR, Chandra S, Vijay V (2004) Duality in linear programming with fuzzy parameters and matrix games with fuzzy pay-offs. Fuzzy Sets Syst 146(2):253–269. https://doi.org/10.1016/S0165-0114(03)00260-4
Bhaumik A, Roy SK, Li DF (2017) Analysis of triangular intuitionistic fuzzy matrix games using robust ranking. J Intell Fuzzy Syst 33(1):327–336. https://doi.org/10.3233/JIFS-161631
Butnariu D (1978) Fuzzy games: A description of the concept. Fuzzy Sets Syst 1(3):181–192. https://doi.org/10.1016/0165-0114(78)90003-9
Campos L (1989) Fuzzy linear programming models to solve fuzzy matrix games. Fuzzy Sets Syst 32(3):275–289. https://doi.org/10.1016/0165-0114(89)90260-1
Cevikel AC, Ahlatolu M (2010) Solutions for fuzzy matrix games. Comput Math Appl 60(3):399–410. https://doi.org/10.1016/j.camwa.2010.04.020
Chaira T (2011) A novel intuitionistic fuzzy C means clustering algorithm and its application to medical images. Appl Soft Comput 11(2):1711–1717. https://doi.org/10.1016/j.asoc.2010.05.005
Chaira T, Panwar A (2014) An Atanassov’s intuitionistic fuzzy kernel clustering for medical image segmentation. Int J Comput Intell Syst 7(2):360–370. https://doi.org/10.1080/18756891.2013.865830
Chen Z, Liu P, Pei Z (2015) An approach to multiple attribute group decision making based on linguistic intuitionistic fuzzy numbers. Int J Comput Intell Syst 8(4):747–760. https://doi.org/10.1080/18756891.2015.1061394
De SK, Biswas R, Roy AR (2001) An application of intuitionistic fuzzy sets in medical diagnosis. Fuzzy Sets Syst 117(2):209–213. https://doi.org/10.1016/S0165-0114(98)00235-8
Dengfeng L, Chuntian C (2002) New similarity measures of intuitionistic fuzzy sets and application to pattern recognitions. Pattern Recogn Lett 23(1–3):221–225. https://doi.org/10.1016/S0167-8655(01)00110-6
Dong Y, Xu Y, Yu S (2009) Computing the numerical scale of the linguistic term set for the 2-tuple fuzzy linguistic representation model. IEEE Trans Fuzzy Syst 17(6):1366–1378. https://doi.org/10.1109/TFUZZ.2009.2032172
Garg H, Kumar K (2018) Some aggregation operators for linguistic intuitionistic fuzzy set and its application to group decision-making process using the set pair analysis. Arabian J Sci Eng 43(6):3213–3227. https://doi.org/10.1007/s13369-017-2986-0
Harsanyi JC (1955) Cardinal Welfare, Individualistic Ethics, and Interpersonal Comparisons of Utility. J Polit Econ 63(4):309–321. https://doi.org/10.2307/1827128
Herrera F, Martínez L (2000) A 2-tuple fuzzy linguistic representation model for computing with words. IEEE Trans Fuzzy Syst 8(6):746–752. https://doi.org/10.1109/91.890332
Hung W, Yang M (2008) On the J-divergence of intuitionistic fuzzy sets with its application to pattern recognition. Inf Sci 178(6):1641–1650. https://doi.org/10.1016/j.ins.2007.11.006
Jaeger G (2008) Applications of game theory in linguistics. Lang Linguis Compass 2(3):406–421. https://doi.org/10.1111/j.1749-818X.2008.00053.x
Kapliński O, Tamošaitiene J (2010) Game theory applications in construction engineering and management. Lang Linguis Compass 16(02):348–363
Khan I, Aggarwal A, Mehra A, Chandra S (2017) Solving matrix games with Atanassov’s I-fuzzy goals via indeterminacy resolution approach. J Inf Optim Sci 38(2):259–287. https://doi.org/10.1080/02522667.2016.1164999
Leng M, Parlar M (2005) Game theoretic applications in supply chain management: A review. INFOR 43(3):187–220. https://doi.org/10.1080/03155986.2005.11732725
Li DF (2010) Mathematical-programming approach to matrix games with payoffs represented by Atanassovs interval-valued intuitionistic fuzzy sets. IEEE Trans Fuzzy Syst 18(6):1112–1128. https://doi.org/10.1109/TFUZZ.2010.2065812
Li DF, Nan JX (2009) A nonlinear programming approach to matrix games with payoffs of atanassov’s intuitionistic fuzzy sets. Int J Uncertainty Fuzziness Knowl Based Syst 17(4):585–607. https://doi.org/10.1142/S0218488509006157
Madani K (2010) Game theory and water resources. J Hydrol 381(3–4):225–238. https://doi.org/10.1016/j.jhydrol.2009.11.045
Maeda T (2003) On characterization of equilibrium strategy of two-person zero-sum games with fuzzy payoffs. Fuzzy Sets Syst 139(2):283–296. https://doi.org/10.1016/S0165-0114(02)00509-2
Maheshwari S, Srivastava A (2016) Study on divergence measures for intuitionistic fuzzy sets and its application in medical diagnosis. J Appl Anal Comput 6(3):772–789
McFadden DW, Tsai M, Kadry B, Souba WW (2012) Game theory: applications for surgeons and the operating room environment. Surg (United States) 152(5):915–922. https://doi.org/10.1016/j.surg.2012.06.019
Muggy L, Heier Stamm JL (2014) Game theory applications in humanitarian operations: a review. J Human Logist Supply Chain Manage 4(1):4–23. https://doi.org/10.1108/JHLSCM-07-2013-0026
Nagurney A, Daniele P, Shukla S (2017) A supply chain network game theory model of cybersecurity investments with nonlinear budget constraints. Ann Oper Res 248(1–2):405–427. https://doi.org/10.1007/s10479-016-2209-1
Nan JX, Li DF, An JJ (2017) Solving bi-matrix games with intuitionistic fuzzy goals and intuitionistic fuzzy payoffs. J Intell Fuzzy Syst 33(6):3723–3732. https://doi.org/10.3233/JIFS-17595
Naqvi D, Aggarwal A, Sachdev G, Khan I (2019) Solving I-fuzzy two-person zero-sum matrix games: Tanaka and Asai approach. Granular Computing 1–11. https://doi.org/10.1007/s41066-019-00200-7
Von Neumann J, Morgenstern O (1953) Theory of Games and Economic Behavior. Princeton University Press, New Jersy. https://doi.org/10.2307/j.ctt1r2gkx
Peng HG, Wang JQ, Cheng PF (2018) A linguistic intuitionistic multi-criteria decision-making method based on the Frank Heronian mean operator and its application in evaluating coal mine safety. Int J Mach Learn Cybernet 9(6):1053–1068. https://doi.org/10.1007/s13042-016-0630-z
Sakawa M, Nishizaki I (1994) Max-min solutions for fuzzy multiobjective matrix games. Fuzzy Sets Syst 67(1):53–69. https://doi.org/10.1016/0165-0114(94)90208-9
Sanchez-Soriano J (2013) An overview on game theory applications to engineering. Int Game Theory Rev 15(3):1340019. https://doi.org/10.1142/S0219198913400197
Seikh MR, Nayak PK, Pal M (2015) Matrix games with intuitionistic fuzzy pay-offs. J Inf Optim Sci 36(1–2):159–181. https://doi.org/10.1080/02522667.2014.961785
Singh A, Gupta A, Mehra A (2020) Matrix games with 2-tuple linguistic information. Ann Oper Res 287(2):895–910. https://doi.org/10.1007/s10479-018-2810-6
Verma R (2020) On aggregation operators for linguistic trapezoidal fuzzy intuitionistic fuzzy sets and their application to multiple attribute group decision making. J Intell Fuzzy Syst 38(3):2907–2950. https://doi.org/10.3233/JIFS-181197
Verma R (2021) On intuitionistic fuzzy order-\(\alpha \) divergence and entropy measures with MABAC method for multiple attribute group decision-making. J Intell Fuzzy Syst. https://doi.org/10.3233/JIFS-201540
Verma T, Kumar A (2018) Ambika methods for solving matrix games with Atanassov’s intuitionistic fuzzy payoffs. IEEE Trans Fuzzy Syst 26(1):270–283. https://doi.org/10.1109/TFUZZ.2017.2651103
Verma R, Sharma BD (2012) On generalized intuitionistic fuzzy divergence (relative information) and their properties. J Uncertain Syst 6(4):308–320
Verma R, Sharma BD (2013) Intuitionistic fuzzy Jensen-Rényi divergence: applications to multiple-attribute decision making. Informatica 37(4):399–409
Verma R, Sharma BD (2014) A new measure of inaccuracy with its application to multi-criteria decision making under intuitionistic fuzzy environment. J Intell Fuzzy Syst 27(4):1811–1824. https://doi.org/10.3233/IFS-141148
Verma R, Sharma BD (2015) Intuitionistic fuzzy Einstein prioritized weighted average operators and their application to multiple attribute group decision making. Appl Math Inf Sci 9(6):3095–3107. https://doi.org/10.12785/amis/090639
Vidyottama V, Chandra S, Bector CR (2004) Bi-matrix games with fuzzy goals and fuzzy pay-offs. Fuzzy Optim Decis Making 3(4):327–344. https://doi.org/10.1007/s10700-004-4202-4
Vijay V, Chandra S, Bector CR (2005) Matrix games with fuzzy goals and fuzzy payoffs. Omega 33(5):425–429. https://doi.org/10.1016/j.omega.2004.07.007
Vlachos I, Sergiadis G (2007) Intuitionistic fuzzy information- applications to pattern recognition. Pattern Recogn Lett 28(2):197–206. https://doi.org/10.1016/j.patrec.2006.07.004
Wang JQ, Wu JT, Wang J, Zhang HY, Chen XH (2014) Interval-valued hesitant fuzzy linguistic sets and their applications in multi-criteria decision-making problems. Inf Sci 288(1):55–72. https://doi.org/10.1016/j.ins.2014.07.034
Xia M (2018) Interval-valued intuitionistic fuzzy matrix games based on Archimedean t-conorm and t-norm. Int J Gen Syst 47(3):278–293. https://doi.org/10.1080/03081079.2017.1413100
Xu Z (2007). A method for multiple attribute decision making with incomplete weight information in linguistic setting. https://doi.org/10.1016/j.knosys.2006.10.002
Zadeh L (1975) The concept of a linguistic variable and its application to approximate reasoning-II. Inf Sci 8(4):301–357. https://doi.org/10.1016/0020-0255(75)90046-8
Zadeh LA (1975) The concept of a linguistic variable and its application to approximate reasoning-I. Inf Sci 8(3):43–80. https://doi.org/10.1016/0020-0255(75)90036-5
Zhang H (2014) Linguistic intuitionistic fuzzy sets and application in MAGDM. J Appl Math. https://doi.org/10.1155/2014/432092
Acknowledgements
The work was financial supported by the Chilean Government (Conicyt) through the Fondecyt Postdoctoral Program (Project Number 3170556).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Ethical approval
This article does not contain any studies with human participants or animals performed by the author.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Verma, R., Aggarwal, A. Matrix games with linguistic intuitionistic fuzzy Payoffs : Basic results and solution methods. Artif Intell Rev 54, 5127–5162 (2021). https://doi.org/10.1007/s10462-021-10014-2
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10462-021-10014-2
Keywords
- Matrix game
- Linguitic intuitionisctic fuzzy numbers
- Aggregation operators
- Linear and nonlinear programming problems