A new interval type-2 trapezoid fuzzy multi-attribute group decision-making method and its application to the evaluation of sponge city construction

Abstract

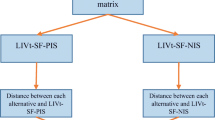
The concept of sponge city receives more and more attention by Chinese government, and the evaluation of sponge city construction is an important aspect. To cope with the complexity and uncertainty of the evaluation process, this paper adopts interval type-2 trapezoidal fuzzy numbers (IT2TFNs) to express decision-making information and develops an approach for evaluating sponge city construction. To do these, two prioritized-guided interval type-2 trapezoidal fuzzy Hamacher operators are first defined to infuse IT2TFNs offered by experts, which can cope with the situation where there is prioritization among experts/attributes. In order to further consider the interactions among experts/attributes, two generalized-Shapley interval type-2 trapezoidal fuzzy prioritized Hamacher Choquet integral operators are presented. To measure the discrimination degree between IT2TFNs, a new interval type-2 trapezoidal fuzzy cross-entropy is defined. After that, cross-entropy based models for obtaining the optimal fuzzy measure on the expert/attribute set are constructed to handle the situation where the weighting information is interactive and partly known. Furthermore, an interval type-2 trapezoidal fuzzy multi-attribute group decision-making approach is developed. Finally, a practical example about the evaluation of residential land design plans in sponge city is provided to illustrate the utilization of the new method, and comparison analysis is provided.

Appendices

Appendix 1: Hamacher operations on IT2TFNs

Let $\tilde{A}_{1}$ = ($\tilde{A}_{1}^{U}$, $\tilde{A}_{1}^{L}$) = ($a_{11}^{U}$, $a_{12}^{U}$, $a_{13}^{U}$, $a_{14}^{U}$; $H(\tilde{A}_{1}^{U} )$), ($a_{11}^{L}$, $a_{12}^{L}$, $a_{13}^{L}$, $a_{14}^{L}$; $H(\tilde{A}_{1}^{L} )$) and $\tilde{A}_{2}$ = ($\tilde{A}_{2}^{U}$, $\tilde{A}_{2}^{L}$) = ($a_{21}^{U}$, $a_{22}^{U}$, $a_{23}^{U}$, $a_{24}^{U}$; $H(\tilde{A}_{2}^{U} )$), ($a_{21}^{L}$, $a_{22}^{L}$, $a_{23}^{L}$, $a_{24}^{L}$; $H(\tilde{A}_{2}^{L} )$) be two non-negative IT2TFNs, where $a_{14}^{U} ,a_{24}^{U} \le 1$, and $\gamma > 0$. The Hamacher operations between $\tilde{A}_{1}$ and $\tilde{A}_{2}$ are defined as follows (Meng and Li 2020):

$$\tilde{A}_{{1}} \oplus_{h} \tilde{A}_{2} = \left( {\begin{array}{*{20}l} {\left( {\begin{array}{*{20}l} {\frac{{a_{11}^{U} + a_{21}^{U} - a_{11}^{U} \times a_{21}^{U} - (1 - \gamma )a_{11}^{U} \times a_{21}^{U} }}{{1 - (1 - \gamma )a_{11}^{U} \times a_{21}^{U} }},\frac{{a_{12}^{U} + a_{22}^{U} - a_{12}^{U} \times a_{22}^{U} - (1 - \gamma )a_{12}^{U} \times a_{22}^{U} }}{{1 - (1 - \gamma )a_{12}^{U} \times a_{22}^{U} }},} \hfill \\ {\frac{{a_{13}^{U} + a_{23}^{U} - a_{13}^{U} \times a_{23}^{U} - (1 - \gamma )a_{13}^{U} \times a_{23}^{U} }}{{1 - (1 - \gamma )a_{13}^{U} \times a_{23}^{U} }},\frac{{a_{14}^{U} + a_{24}^{U} - a_{14}^{U} \times a_{24}^{U} - (1 - \gamma )a_{14}^{U} \times a_{24}^{U} }}{{1 - (1 - \gamma )a_{14}^{U} \times a_{24}^{U} }};} \hfill \\ {\frac{{H\left( {\tilde{A}_{1}^{U} } \right){ + }H\left( {\tilde{A}_{2}^{U} } \right) - H\left( {\tilde{A}_{1}^{U} } \right) \times H\left( {\tilde{A}_{2}^{U} } \right) - (1 - \gamma )H\left( {\tilde{A}_{1}^{U} } \right) \times H(\tilde{A}_{2}^{U} )}}{{1 - (1 - \gamma )H\left( {\tilde{A}_{1}^{U} } \right) \times H\left( {\tilde{A}_{2}^{U} } \right)}}} \hfill \\ \end{array} \left( {\tilde{A}_{2}^{U} } \right)} \right)} \hfill \\ {\left( {\begin{array}{*{20}l} {\frac{{a_{11}^{L} + a_{21}^{L} - a_{11}^{L} \times a_{21}^{L} - (1 - \gamma )a_{11}^{L} \times a_{21}^{L} }}{{1 - (1 - \gamma )a_{11}^{L} \times a_{21}^{L} }},\frac{{a_{12}^{L} + a_{22}^{L} - a_{12}^{L} \times a_{22}^{L} - (1 - \gamma )a_{12}^{L} \times a_{22}^{L} }}{{1 - (1 - \gamma )a_{12}^{L} \times a_{22}^{L} }},} \hfill \\ {\frac{{a_{13}^{L} + a_{23}^{L} - a_{13}^{L} \times a_{23}^{L} - (1 - \gamma )a_{13}^{L} \times a_{23}^{L} }}{{1 - (1 - \gamma )a_{13}^{L} \times a_{23}^{L} }},\frac{{a_{14}^{L} + a_{24}^{L} - a_{14}^{L} \times a_{24}^{L} - (1 - \gamma )a_{14}^{L} \times a_{24}^{L} }}{{1 - (1 - \gamma )a_{14}^{L} \times a_{24}^{L} }};} \hfill \\ {\frac{{H\left( {\tilde{A}_{1}^{L} } \right){ + }H\left( {\tilde{A}_{2}^{L} } \right) - H\left( {\tilde{A}_{2}^{L} } \right) \times H\left( {\tilde{A}_{2}^{L} } \right) - (1 - \gamma )H\left( {\tilde{A}_{1}^{L} } \right) \times H\left( {\tilde{A}_{2}^{L} } \right)}}{{1 - (1 - \gamma )\left( {\tilde{A}_{1}^{L} } \right) \times H\left( {\tilde{A}_{2}^{L} } \right)}}} \hfill \\ \end{array} } \right)} \hfill \\ \end{array} } \right),$$

$$\tilde{A}_{{1}} \otimes_{h} \tilde{A}_{2} = \left( {\begin{array}{*{20}l} {\left( {\begin{array}{*{20}l} {\frac{{a_{11}^{U} \times a_{21}^{U} }}{{\gamma + ({1} - \gamma )\left( {a_{11}^{U} + a_{21}^{U} - a_{11}^{U} \times a_{21}^{U} } \right)}},\frac{{a_{12}^{U} \times a_{22}^{U} }}{{\gamma + ({1} - \gamma )\left( {a_{12}^{U} + a_{22}^{U} - a_{12}^{U} \times a_{22}^{U} } \right)}},} \hfill \\ {\frac{{a_{13}^{U} \times a_{23}^{U} }}{{\gamma + ({1} - \gamma )\left( {a_{13}^{U} + a_{23}^{U} - a_{13}^{U} \times a_{23}^{U} } \right)}},\frac{{a_{14}^{U} \times a_{24}^{U} }}{{\gamma + ({1} - \gamma )\left( {a_{14}^{U} + a_{24}^{U} - a_{14}^{U} \times a_{24}^{U} } \right)}};} \hfill \\ {\frac{{H\left( {\tilde{A}_{1}^{U} } \right) \times H\left( {\tilde{A}_{2}^{U} } \right)}}{{\gamma + ({1} - \gamma )\left( {H\left( {\tilde{A}_{1}^{U} } \right) + H\left( {\tilde{A}_{2}^{U} } \right) - H\left( {\tilde{A}_{1}^{U} } \right) \times H\left( {\tilde{A}_{2}^{U} } \right)} \right)}}} \hfill \\ \end{array} } \right)} \hfill \\ {\left( {\begin{array}{*{20}l} {\frac{{a_{11}^{L} \times a_{21}^{L} }}{{\gamma + ({1} - \gamma )\left( {a_{11}^{L} + a_{21}^{L} - a_{11}^{L} \times a_{21}^{L} } \right)}},\frac{{a_{12}^{L} \times a_{22}^{L} }}{{\gamma + ({1} - \gamma )\left( {a_{12}^{L} + a_{22}^{L} - a_{12}^{L} \times a_{22}^{L} } \right)}},} \hfill \\ {\frac{{a_{13}^{L} \times a_{23}^{L} }}{{\gamma + ({1} - \gamma )\left( {a_{13}^{L} + a_{23}^{L} - a_{13}^{L} \times a_{23}^{L} } \right)}},\frac{{a_{14}^{L} \times a_{24}^{L} }}{{\gamma + ({1} - \gamma )\left( {a_{14}^{L} + a_{24}^{L} - a_{14}^{L} \times a_{24}^{L} } \right)}};} \hfill \\ {\frac{{H\left( {\tilde{A}_{1}^{L} } \right) \times H\left( {\tilde{A}_{2}^{L} } \right)}}{{\gamma + ({1} - \gamma )\left( {H\left( {\tilde{A}_{1}^{L} } \right) + H(\tilde{A}_{2}^{L} ) - H\left( {\tilde{A}_{1}^{K} } \right) \times H\left( {\tilde{A}_{2}^{L} } \right)} \right)}}} \hfill \\ \end{array} } \right)} \hfill \\ \end{array} } \right),$$

$$\lambda \tilde{A}_{1} = \left( {\begin{array}{*{20}l} {\left( {\begin{array}{*{20}l} {\frac{{\left( {1 + (\gamma - 1)a_{11}^{U} } \right)^{\lambda } - \left( {1 - a_{11}^{U} } \right)^{\lambda } }}{{\left( {1 + (\gamma - 1)a_{11}^{U} } \right)^{\lambda } + (\gamma - 1)(1 - a_{11}^{U} )^{\lambda } }},\frac{{\left( {1 + (\gamma - 1)a_{12}^{U} } \right)^{\lambda } - \left( {1 - a_{12}^{U} } \right)^{\lambda } }}{{\left( {1 + (\gamma - 1)a_{12}^{U} } \right)^{\lambda } + (\gamma - 1)\left( {1 - a_{12}^{U} } \right)^{\lambda } }},} \hfill \\ {\frac{{\left( {1 + (\gamma - 1)a_{13}^{U} } \right)^{\lambda } - \left( {1 - a_{13}^{U} } \right)^{\lambda } }}{{\left( {1 + (\gamma - 1)a_{13}^{U} } \right)^{\lambda } + (\gamma - 1)\left( {1 - a_{13}^{U} } \right)^{\lambda } }},\frac{{\left( {1 + (\gamma - 1)a_{14}^{U} } \right)^{\lambda } - \left( {1 - a_{14}^{U} } \right)^{\lambda } }}{{\left( {1 + (\gamma - 1)a_{14}^{U} } \right)^{\lambda } + (\gamma - 1)\left( {1 - a_{14}^{U} } \right)^{\lambda } }};} \hfill \\ {\frac{{\left( {1 + (\gamma - 1)H\left( {\tilde{A}_{1}^{U} } \right)} \right)^{\lambda } - \left( {1 - H\left( {\tilde{A}_{1}^{U} } \right)} \right)^{\lambda } }}{{\left( {1 + (\gamma - 1)H\left( {\tilde{A}_{1}^{U} } \right)} \right)^{\lambda } + (\gamma - 1)\left( {1 - H\left( {\tilde{A}_{1}^{U} } \right)} \right)^{\lambda } }}} \hfill \\ \end{array} } \right)} \hfill \\ {\left( {\begin{array}{*{20}l} {\frac{{\left( {1 + (\gamma - 1)a_{11}^{L} } \right)^{\lambda } - \left( {1 - a_{11}^{L} } \right)^{\lambda } }}{{\left( {1 + (\gamma - 1)a_{11}^{L} } \right)^{\lambda } + (\gamma - 1)\left( {1 - a_{11}^{L} } \right)^{\lambda } }},\frac{{\left( {1 + (\gamma - 1)a_{12}^{L} } \right)^{\lambda } - \left( {1 - a_{12}^{L} } \right)^{\lambda } }}{{\left( {1 + (\gamma - 1)a_{12}^{L} } \right)^{\lambda } + (\gamma - 1)\left( {1 - a_{12}^{L} } \right)^{\lambda } }},} \hfill \\ {\frac{{\left( {1 + (\gamma - 1)a_{13}^{L} } \right)^{\lambda } - \left( {1 - a_{13}^{L} } \right)^{\lambda } }}{{\left( {1 + (\gamma - 1)a_{13}^{L} } \right)^{\lambda } + (\gamma - 1)\left( {1 - a_{13}^{L} } \right)^{\lambda } }},\frac{{\left( {1 + (\gamma - 1)a_{14}^{L} } \right)^{\lambda } - \left( {1 - a_{14}^{L} } \right)^{\lambda } }}{{\left( {1 + (\gamma - 1)a_{14}^{L} } \right)^{\lambda } + (\gamma - 1)\left( {1 - a_{14}^{L} } \right)^{\lambda } }};} \hfill \\ {\frac{{\left( {1 + (\gamma - 1)H\left( {\tilde{A}_{1}^{L} } \right)} \right)^{\lambda } - \left( {1 - H\left( {\tilde{A}_{1}^{L} } \right)} \right)^{\lambda } }}{{\left( {1 + (\gamma - 1)H\left( {\tilde{A}_{1}^{L} } \right)} \right)^{\lambda } + (\gamma - 1)\left( {1 - H\left( {\tilde{A}_{1}^{L} } \right)} \right)^{\lambda } }}} \hfill \\ \end{array} } \right)} \hfill \\ \end{array} } \right),$$

$$\tilde{A}_{1}^{\lambda } = \left( {\begin{array}{*{20}l} {\left( {\begin{array}{*{20}l} {\frac{{\gamma \left( {a_{11}^{U} } \right)^{\lambda } }}{{\left( {1 + (\gamma - 1)\left( {1 - a_{11}^{U} } \right)} \right)^{\lambda } + (\gamma - 1)\left( {a_{11}^{U} } \right)^{\lambda } }},\frac{{\gamma \left( {a_{12}^{U} } \right)^{\lambda } }}{{\left( {1 + (\gamma - 1)\left( {1 - a_{12}^{U} } \right)} \right)^{\lambda } + (\gamma - 1)\left( {a_{12}^{U} } \right)^{\lambda } }},} \hfill \\ {\frac{{\gamma (a_{13}^{U} )^{\lambda } }}{{\left( {1 + (\gamma - 1)(1 - a_{13}^{U} )} \right)^{\lambda } + (\gamma - 1)(a_{13}^{U} )^{\lambda } }},\frac{{\gamma (a_{14}^{U} )^{\lambda } }}{{\left( {1 + (\gamma - 1)\left( {1 - a_{14}^{U} } \right)} \right)^{\lambda } + (\gamma - 1)\left( {a_{14}^{U} } \right)^{\lambda } }};} \hfill \\ {\frac{{\gamma \left( {H\left( {\tilde{A}_{1}^{U} } \right)} \right)^{\lambda } }}{{\left( {1 + (\gamma - 1)\left( {1 - H\left( {\tilde{A}_{1}^{U} } \right)} \right)} \right)^{\lambda } + (\gamma - 1)\left( {H\left( {\tilde{A}_{1}^{U} } \right)} \right)^{\lambda } }}} \hfill \\ \end{array} } \right)} \hfill \\ {\left( {\begin{array}{*{20}l} {\frac{{\gamma \left( {a_{11}^{L} } \right)^{\lambda } }}{{\left( {1 + (\gamma - 1)\left( {1 - a_{11}^{L} } \right)} \right)^{\lambda } + (\gamma - 1)\left( {a_{11}^{L} } \right)^{\lambda } }},\frac{{\gamma \left( {a_{12}^{L} } \right)^{\lambda } }}{{\left( {1 + (\gamma - 1)\left( {1 - a_{12}^{L} } \right)} \right)^{\lambda } + (\gamma - 1)\left( {a_{12}^{L} } \right)^{\lambda } }},} \hfill \\ {\frac{{\gamma \left( {a_{13}^{L} } \right)^{\lambda } }}{{\left( {1 + (\gamma - 1)\left( {1 - a_{13}^{L} } \right)} \right)^{\lambda } + (\gamma - 1)\left( {a_{13}^{L} } \right)^{\lambda } }},\frac{{\gamma \left( {a_{14}^{L} } \right)^{\lambda } }}{{\left( {1 + (\gamma - 1)\left( {1 - a_{14}^{L} } \right)} \right)^{\lambda } + (\gamma - 1)\left( {a_{14}^{L} } \right)^{\lambda } }};} \hfill \\ {\frac{{\gamma \left( {H\left( {\tilde{A}_{1}^{L} } \right)} \right)^{\lambda } }}{{\left( {1 + (\gamma - 1)\left( {1 - H\left( {\tilde{A}_{1}^{L} } \right)} \right)} \right)^{\lambda } + (\gamma - 1)\left( {H\left( {\tilde{A}_{1}^{L} } \right)} \right)^{\lambda } }}} \hfill \\ \end{array} } \right)} \hfill \\ \end{array} } \right).$$

Appendix 2: The normalization of IT2TFNs.

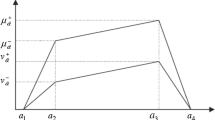
Let $\tilde{A}_{i}$ = ($\tilde{A}_{i}^{U}$, $\tilde{A}_{i}^{L}$) = ($a_{i1}^{U}$, $a_{i2}^{U}$, $a_{i3}^{U}$, $a_{i4}^{U}$; $H(\tilde{A}_{i}^{U} )$), ($a_{i1}^{L}$, $a_{i2}^{L}$, $a_{i3}^{L}$, $a_{i4}^{L}$; $H(\tilde{A}_{i}^{L} )$), i = 1, 2, …, n, be a collection of IT2TFNs.$\tilde{A}_{i}$ is normalized into $\tilde{A}_{i}^{\prime \prime }$ by the following formula (Meng and Li 2020):

$$\begin{aligned} \tilde{A}_{i}^{\prime \prime } & { = }\left( {\tilde{A}_{i}^{\prime \prime U} ,\tilde{A}_{i}^{\prime \prime L} } \right) \\ & = \left( {\left( {a_{i1}^{\prime \prime U} ,a_{i2}^{\prime \prime U} ,a_{i3}^{\prime \prime U} ,a_{i4}^{\prime \prime U} ;H\left( {\tilde{A}_{i}^{\prime \prime U} } \right)} \right),\left( {a_{i1}^{\prime \prime L} ,a_{i2}^{\prime \prime L} ,a_{i3}^{\prime \prime L} ,a_{i4}^{\prime \prime L} ;H\left( {\tilde{A}_{i}^{\prime \prime L} } \right)} \right)} \right) \\ & = \left( {\left( {\frac{{a_{i1}^{U} }}{{a_{m} }},\frac{{a_{i2}^{U} }}{{a_{m} }},\frac{{a_{i3}^{U} }}{{a_{m} }},\frac{{a_{i4}^{U} }}{{a_{m} }};\frac{{H\left( {\tilde{A}_{i}^{U} } \right)}}{{H_{m} }}} \right),\;\left( {\frac{{a_{i1}^{L} }}{{a_{m} }},\frac{{a_{i2}^{L} }}{{a_{m} }},\frac{{a_{i3}^{L} }}{{a_{m} }},\frac{{a_{i4}^{L} }}{{a_{m} }};\frac{{H\left( {\tilde{A}_{i}^{L} } \right)}}{{H_{m} }}} \right)} \right), \\ \end{aligned}$$

where $a_{m}$ = $\max a_{i4}^{U}$, and $H_{m}$ = $\max H(\tilde{A}_{i}^{U} )$ for all i = 1, 2, …, n.