Failure mode and effect analysis approach considering risk attitude of dynamic reference point cumulative prospect theory in uncertainty contexts

Abstract

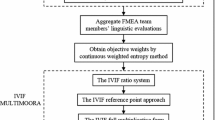
Failure mode and effect analysis (FMEA) method is widely utilized as a powerful reliability management tool to effectively evaluate and prevent risk problems that occur in all aspects of production, service and transportation. Since FMEA experts have different professional backgrounds and the particularity of the risk assessment environment, they may show different risk attitudes and bounded rational behavior. Thus, this paper develops an FMEA framework based on the dynamic reference point cumulative prospect theory considering risk attitude. The linguistic distribution assessment (LDA) and linguistic scale function are utilized to indicate the risk attitude based personalized FMEA experts’ evaluation information. Further, based on the idea of maximizing deviation and the LDA-EMD (earth mover’s distance) formula, the criteria weight determination method considering the different risk attitudes of the FMEA expert is constructed. Then, a dynamic reference point cumulative prospect theory considering different risk attitudes is developed to obtain the prospect value of the failure modes (FMs) under each FMEA expert. The comprehensive expert weight determination method is established which takes the subjective and objective aspects of expert evaluation and revision factor into account. Finally, the numerical example is carried out to verify the validity and superiority performance of the proposed FMEA method. The improved FMEA method can enhance the flexibility and reliability of risk assessment. Findings proved that it is necessary to consider the different and dynamic risk attitudes of experts in the practical risk assessment.

Appendices

Appendix 1

See Tables

Table 11 Seven-grade linguistic scale for occurrence (Liu et al. 2019b)

11,

Table 12 Seven-grade linguistic scale for severity (Liu et al. 2019b)

12,

Table 13 Seven-grade linguistic scale for detection (Liu et al. 2019b)

13,

Table 14 Seven-grade linguistic scale for cost (Liu et al. 2019b)

14,

Table 15 Seven-grade linguistic scale for green (Liu et al. 2019b)

15.

Appendix 2

Example 1

Suppose $m_{1} = \left\{ {\iota_{0} \left( {0.3} \right),\iota_{1} \left( {0.4} \right),\iota_{2} \left( {0.3} \right)} \right\}$ and $m_{2} = \left\{ {\iota_{0} \left( {0.2} \right),\iota_{1} \left( {0.8} \right),\iota_{2} \left( 0 \right)} \right\}$ are two LDAs with respect to $S = \left\{ {\iota_{{0}} = bad,\iota_{{1}} = medium,\iota_{2} = good} \right\}$. Then, it can get the proportional vector of the two LDAs: $P = \left\{ {0.3,0.4,0.3} \right\}$, $Q = \left\{ {0.2,0.8,0} \right\}$; and utilize the formula (1), the cost between two adjacent LTs can be shown in the Table

Table 16 The cost between two adjacent linguistic terms

16.

Hence, the linear programming model is established to transform P into Q with minimum cost.

$$\left| \begin{gathered} \min { 0*}x_{11} + 0.5*x_{12} + x_{13} + 0.5*x_{21} + 0*x_{22} + 0.5*x_{23} + x_{31} + 0.5*x_{32} + 0*x_{33} \hfill \\ s.t. \, \left\{ \begin{gathered} {\text{ x}}_{11} + x_{12} + x_{13} = 0.2; \hfill \\ \, x_{21} + x_{22} + x_{23} = 0.8; \hfill \\ x_{31} + x_{32} + x_{33} = 0; \hfill \\ x_{11} + x_{21} + x_{31} = 0.3; \hfill \\ x_{12} + x_{22} + x_{32} = 0.4; \hfill \\ x_{13} + x_{23} + x_{33} = 0.3; \hfill \\ x_{11} + x_{12} + x_{13} + x_{21} + x_{22} + x_{23} + x_{31} + x_{32} + x_{33} = 1 \hfill \\ x_{11} ,x_{12} ,x_{13} ,x_{21} ,x_{22} ,x_{23} ,x_{31} ,x_{32} ,x_{33} \ge 0. \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} \right.$$

$LDA{ - }EMD\left( {m_{1} ,m_{2} } \right) = \frac{{\sum\limits_{i = 1}^{g + 1} {\sum\limits_{j = 1}^{g + 1} {c_{ij} x_{ij} } } }}{{\sum\limits_{i = 1}^{g + 1} {\sum\limits_{j = 1}^{g + 1} {x_{ij} } } }} = 0.2$.

In order to show more clearly how LDA-EMD distance transforms P into Q at the minimum cost, the adjustment process of transform P into Q with minimum cost can visual shown as Fig. 2 (Fig. 

Fig. 9

The adjustment process of transform P into Q with minimum cost

9).

Then, through the formula (10), it can get the distance between the m₁ and m₂ is: 0.2.

And the similarity between the m₁ and m₂ is:

$$s\left( {m_{1} ,m_{2} } \right) = 1 - LDA{ - }EMD\left( {m_{1} ,m_{2} } \right) = 1 - 0.2 = 0.8.$$

Appendix 3

Tables

Table 17 The decision matrix with the LDA for expert1

17,

Table 18 The decision matrix with the LDA for expert2

18,

Table 19 The decision matrix with the LDA for expert3

19,

Table 20 The decision matrix with the LDA for expert4

20,

Table 21 The decision matrix with the LDA for expert5

21,

Table 22 The evaluation of the experts’ reliability

22.

Appendix 4

See Table

Table 23 The collective decision matrix with LDA

23.

Appendix 5

See Tables

Table 24 The reference point value of the expert 1

24,

Table 25 The reference point value of the expert 2

25,

Table 26 The reference point value of the expert 3

26,

Table 27 The reference point value of the expert 4

27,

Table 28 The reference point value of the expert 5

28,

Table 29 The degree of consensus between the experts

29,

Table 30 The prospect value of expert for every FM

30.

Appendix 6

See Table

Table 31 The different setting of attribute weights

31.

Appendix 7

In order to show the advantages of the distance formula proposed in this paper more clearly, this paper use the four LDA distance formulas proposed in the past and the distance formula proposed in this paper to calculate different examples.

The LDA distance proposed by other researches are presented as follows:

(i) Distance formula 1 (Zhang et al. 2014): $d\left( {m_{1} ,m_{2} } \right) = \frac{1}{2}\sum\limits_{k = 0}^{g - 1} {\left| {\beta_{k}^{1} - \beta_{k}^{2} } \right|}$;

(ii) Distance formula 2 (Zhang et al. 2017): $d\left( {m_{1} ,m_{2} } \right) = \frac{1}{g - 1}\sum\limits_{k = 0}^{g - 1} {\left| {\beta_{k}^{1} - \beta_{k}^{2} } \right|k}$;

(iii) Distance formula 3 (Yu et al. 2018): $d\left( {m_{1} ,m_{2} } \right) = \left[ {\frac{1}{2}\left( \begin{gathered} \frac{1}{{\# m_{1} }}\sum\limits_{{\left( {s_{1}^{k1} ,\beta_{1}^{k1} } \right) \in m_{1} }}^{{}} {\min_{{\left( {s_{2}^{k2} ,\beta_{2}^{k2} } \right) \in m_{2} }} \left( {\left| {f\left( {s_{1}^{k1} } \right)\beta_{1}^{k1} - f\left( {s_{2}^{k2} } \right)\beta_{2}^{k2} } \right|} \right)^{r} } + \hfill \\ \frac{1}{{\# m_{2} }}\sum\limits_{{\left( {s_{2}^{k2} ,\beta_{2}^{k2} } \right) \in m_{2} }}^{{}} {\min_{{\left( {s_{1}^{k1} ,\beta_{1}^{k1} } \right) \in m_{1} }} \left( {\left| {f\left( {s_{1}^{k1} } \right)\beta_{1}^{k1} - f\left( {s_{2}^{k2} } \right)\beta_{2}^{k2} } \right|} \right)^{r} } \hfill \\ \end{gathered} \right)} \right]^{\frac{1}{r}}$;

(iv) Distance formula 4 (Yao 2018): $d\left( {m_{1} ,m_{2} } \right) = \frac{1}{g - 1}\sum\limits_{k = 0}^{g - 1} {\left| {\sum\limits_{r = 0}^{k} {\beta_{r}^{1} } - \sum\limits_{r = 0}^{k} {\beta_{r}^{2} } } \right|}$;

And the specific examples are shown as follows:

Example 2

Let $m_{1} = \left\{ {\iota_{0} \left( 0 \right),\iota_{1} \left( {0.5} \right),\iota_{2} \left( {0.5} \right)} \right.,\iota_{3} \left( 0 \right),\iota_{4} \left( 0 \right)\left. {,\iota_{5} \left( 0 \right),\iota_{6} \left( 0 \right)} \right\}$,$m_{2} = \left\{ {\iota_{0} \left( 0 \right),\iota_{1} \left( 0 \right),\iota_{2} \left( 0 \right),} \right.\iota_{3} \left( {0.5} \right),\iota_{4} \left( {0.5} \right)$ $\left. {,\iota_{5} \left( 0 \right),\iota_{6} \left( 0 \right)} \right\}$ and $m_{3} = \left\{ {\iota_{0} \left( 0 \right),\iota_{1} \left( 0 \right),\iota_{2} \left( 0 \right)} \right.,\iota_{3} \left( 0 \right),\iota_{4} \left( 0 \right)\left. {,\iota_{5} \left( {0.5} \right),\iota_{6} \left( {0.5} \right)} \right\}$ be any three LDAs with respect to $S$($S$ is the 7-scale linguistic term set and the deviation of adjacent semantics is balanced). Then, the corresponding distance between $m_{1}$ and $m_{2}$, $m_{1}$ and $m_{3}$ are calculated by the LDA distance formula.

Example 3

Let $m_{1} = \left\{ {\iota_{0} \left( 0 \right),\iota_{1} \left( 0 \right),\iota_{2} \left( {0.1} \right)} \right.,\iota_{3} \left( {0.8} \right),\iota_{4} \left( {0.1} \right)\left. {,\iota_{5} \left( 0 \right),\iota_{6} \left( 0 \right)} \right\}$ and $m_{2} = \left\{ {\iota_{0} \left( 0 \right),\iota_{1} \left( {0.1} \right),\iota_{2} \left( {0.2} \right)} \right.$ $\left. {,\iota_{3} \left( {0.4} \right),\iota_{4} \left( {0.2} \right),\iota_{5} \left( {0.1} \right),\iota_{6} \left( 0 \right)} \right\}$ be any two LDAs with respect to $S$($S$ is the 7-scale linguistic term set and the deviation of adjacent semantics is balanced). Then, the corresponding distance between $m_{1}$ and $m_{2}$ is calculated by the LDA distance formula.

Example 4

Let $m_{1} = \left\{ {\iota_{0} \left( 0 \right),\iota_{1} \left( 0 \right),\iota_{2} \left( 0 \right)} \right.,\iota_{3} \left( 0 \right),\iota_{4} \left( 0 \right)\left. {,\iota_{5} \left( {0.2} \right),\iota_{6} \left( {0.8} \right)} \right\}$,$m_{2} = \left\{ {\iota_{0} \left( 0 \right),\iota_{1} \left( 0 \right),\iota_{2} \left( {0.5} \right)} \right.,\iota_{3} \left( {0.5} \right),\iota_{4} \left( 0 \right)$$\left. {,\iota_{5} \left( 0 \right),\iota_{6} \left( 0 \right)} \right\}$ and $m_{3} = \left\{ {\iota_{0} \left( 0 \right),\iota_{1} \left( 0 \right),\iota_{2} \left( 0 \right)} \right.,\iota_{3} \left( {0.5} \right),\iota_{4} \left( {0.5} \right)\left. {,\iota_{5} \left( 0 \right),\iota_{6} \left( 0 \right)} \right\}$ be any three LDAs with respect to $S$($S$ is the 7-scale linguistic term set and the deviation of adjacent semantics is balanced). Then, the corresponding distance between $m_{1}$ and $m_{2}$, $m_{1}$ and $m_{3}$ are calculated by the LDA distance formula.

Example 5

Let $m_{1} = \left\{ {\iota_{0} \left( 0 \right),\iota_{1} \left( 0 \right),\iota_{2} \left( {0.1} \right)} \right.,\iota_{3} \left( {0.8} \right),\iota_{4} \left( {0.1} \right)\left. {,\iota_{5} \left( 0 \right),\iota_{6} \left( 0 \right)} \right\}$ and $m_{2} = \left\{ {\iota_{0} \left( 0 \right),\iota_{1} \left( {0.1} \right),\iota_{2} \left( {0.2} \right),} \right.$ $\left. {\iota_{3} \left( {0.4} \right),\iota_{4} \left( {0.2} \right),\iota_{5} \left( {0.1} \right),\iota_{6} \left( 0 \right)} \right\}$ be any two LDAs with respect to $S$($S$ is the 7-scale linguistic term set and the deviation of adjacent semantics is unbalanced). Then, the corresponding distance between $m_{1}$ and $m_{2}$ is calculated by the LDA distance formula.