Abstract
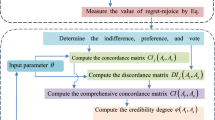
Three-way decision (3WD) can be used to handle complexity and uncertainty in decision-making problems, and is compatible with human cognitive systems. For insufficient existing experiences, decision-makers (DMs) can select interval fuzzy information, as the information about medicine company is more hesitation, imprecision, and ambiguity. In the determination process, DMs may not take suitable decisions by choosing membership and non-membership degree of imprecise information. To improve fault-tolerance and validate the plausibility of DMs’ evaluation, the probabilistic interval-valued q-rung orthopair hesitant fuzzy set (PIVq-ROHFS) is introduced. Additionally, distinct psychological behaviours of DMs have an impact on the outcomes of decision-making. For this situation, we first develop a regret theory based 3WD model in PIVq-ROHFS to evaluate the utility value of the objects. The core focus of regret theory is to develop a new regret-rejoice function based on projection theory. Another core focus of this inquisition is to propose a novel multi-criteria decision making (MCDM) method for evaluating conditional probability in 3WD model. The criteria’s weight in MCDM method is evaluated by a newly proposed multi-objective optimization (MOO) problem. To solve the MOO problem, we utilize a hybrid technique by combining particle swarm optimization and multi-choice goal programming with utility function.








Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Data availability
All data utilized for supporting the findings of this study.
References
Akram M, Bibi R, Deveci M (2023) An outranking approach with 2-tuple linguistic Fermatean fuzzy sets for multi-attribute group decision-making. Eng Appl Artif Intell 121:105992
Ali J (2023) Norm-based distance measure of \(q\)-rung orthopair fuzzy sets and its application in decision-making. Comput Appl Math 42(4):184
Ali J, Bashir Z, Rashid T (2021) WASPAS-based decision making methodology with unknown weight information under uncertain evaluations. Exp Syst Appl 168:114143
Ali J, Bashir Z, Rashid T (2021) Weighted interval-valued dual-hesitant fuzzy sets and its application in teaching quality assessment. Soft Comput 25:3503–3530
Ali J, Bashir Z, Rashid T, Mashwani WK (2022) A \(q\)-rung orthopair hesitant fuzzy stochastic method based on regret theory with unknown weight information. J Amb Intel Hum Comp 14:11935–11952
Ali J, Bashir Z, Rashid T (2022) On distance measure and TOPSIS model for probabilistic interval-valued hesitant fuzzy sets: application to healthcare facilities in public hospitals. Grey Syst Theory Appl 12(1):197–229
Ali J, Bashir Z, Rashid T (2023) A cubic \(q\)-rung orthopair fuzzy TODIM method based on Minkowski-type distance measures and entropy weight. Soft Comput. https://doi.org/10.1007/s00500-023-08552-8
Bashir Z, Ali J, Rashid T (2021) Consensus-based robust decision making methods under a novel study of probabilistic uncertain linguistic information and their application in Forex investment. Artif Intell Rev 54:2091–2132
Bell DE (1982) Regret in decision making under uncertainty. Oper Res 30(5):961–981
Dağıstanlı HA (2023) An Interval-Valued Intuitionistic Fuzzy VIKOR Approach for R&D Project Selection in Defense Industry Investment Decisions. J Soft Comput Decis Anal 2(1). https://doi.org/10.31181/jscda21202428
Debnath K, Roy SK (2023) Power partitioned neutral aggregation operators for T-spherical fuzzy sets: an application to \(H_2\) refuelling site selection. Exp Syst Appl 216:119470
Deng W, Zhao H, Yang X, Xiong J, Sun M, Li B (2017) Study on an improved adaptive PSO algorithm for solving multi-objective gate assignment. Appl Soft Comput 59:288–302
Deng J, Zhan J, Ding W, Liu P, Pedrycz W (2023) A novel prospect-theory-based three-way decision methodology in multi-scale information systems. Artif Intell Rev 56(7):6591–6625
Deveci M, Erdogan N, Cali U, Stekli J, Zhong S (2021) Type-2 neutrosophic number based multi-attributive border approximation area comparison (MABAC) approach for offshore wind farm site selection in USA. Eng Appl Artif Intell 103:104311
Deveci M, Gokasar I, Brito-Parada PR (2022) A comprehensive model for socially responsible rehabilitation of mining sites using \(q\)-rung orthopair fuzzy sets and combinative distance-based assessment. Exp Syst Appl 200:117155
Du J, Liu S, Liu Y (2021) A novel grey multi-criteria three-way decisions model and its application. Comput Ind Eng 158:107405
Gao Y, Li DS, Zhong H (2020) A novel target threat assessment method based on three-way decisions under intuitionistic fuzzy multi-attribute decision making environment. Eng Appl Artif Intell 87:103276
Ghanbari Ghoushchi N, Ahmadzadeh K, Jafarzadeh Ghoushchi S (2023) A New Extended Approach to Reduce Admission Time in Hospital Operating Rooms Based on the FMEA Method in an Uncertain Environment. J Soft Comput Decis Anal 1(1):80–101. https://doi.org/10.31181/jscda11202310
Ghosh S, Küfer KH, Roy SK, Weber GW (2023) Type-2 zigzag uncertain multi-objective fixed-charge solid transportation problem: time window vs. preservation technology. Cent Eur J Oper Res 31:337–362
Giri BK, Roy SK (2022) Neutrosophic multi-objective green four-dimensional fixed-charge transportation problem. Int J Mach Learn Cybern 13(10):3089–3112
Giri BK, Roy SK, Deveci M (2023) Fuzzy robust flexible programming with \(Me\) measure for electric sustainable supply chain. Appl Soft Comput 145:110614
Gurmani SH, Zhang Z, Zulqarnain RM, Askar S (2023) An interaction and feedback mechanism-based group decision-making for emergency medical supplies supplier selection using T-spherical fuzzy information. Sci Rep 13(1):8726
Gurmani SH, Zhang Z, Zulqarnain RM (2023) An integrated group decision-making technique under interval-valued probabilistic linguistic T-spherical fuzzy information and its application to the selection of cloud storage provider. AIMS Math 8(9):20223–20253
Gurmani SH, Chen H, Bai Y (2023) Extension of TOPSIS method under \(q\)-rung orthopair fuzzy hypersoft environment based on correlation coefficients and its applications to multi-attribute group decision-making. Int J Fuzzy Syst 25(2):1–14. https://doi.org/10.1007/s40815-022-01386-w
Joshi BP, Singh A, Bhatt PK, Vaisla KS (2018) Interval valued \(q\)-rung orthopair fuzzy sets and their properties. J Intel Fuzzy Syst 35(5):5225–5230
Li Z, Xie N, Huang D, Zhang G (2020) A three-way decision method in a hybrid decision information system and its application in medical diagnosis. Artif Intell Rev 53:4707–4736
Liang W, Wang YM (2021) A probabilistic interval-valued hesitant fuzzy gained and lost dominance score method based on regret theory. Comput Ind Eng 159:107532
Liang D, Xu Z, Liu D, Wu Y (2018) Method for three-way decisions using ideal TOPSIS solutions at Pythagorean fuzzy information. Inf Sci 435:282–295
Liang D, Fu Y, Xu Z, Tang W (2021) Loss function information fusion and decision rule deduction of three-way decisions by construing interval-valued \(q\)-rung orthopair fuzzy integral. IEEE Trans Fuzzy Syst 30(9):3645–3660
Liu P, Wang Y, Jia F, Fujita H (2020) A multiple attribute decision making three-way model for intuitionistic fuzzy numbers. Int J Approx Reason 119:177–203
Liu Z, Wang X, Li L, Zhao X, Liu P (2021) \(Q\)-rung orthopair fuzzy multiple attribute group decision-making method based on normalized bidirectional projection model and generalized knowledge-based entropy measure. J Amb Intel Hum Comp 12(2):2715–2730
Loomes G, Sugden R (1982) Regret theory: an alternative theory of rational choice under uncertainty. Econ J 92(368):805–824
Maghrabie HF, Beauregard Y, Schiffauerova A (2019) Multi-criteria decision making problems with unknown weight information under uncertain evaluations. Comput Ind Eng 133:131–138
Malik MA, Bashir Z, Rashid T, Ali J (2018) Probabilistic hesitant intuitionistic linguistic term sets in multi-attribute group decision making. Symmetry 10(9):392
Mamashli Z, Nayeri S, Tavakkoli-Moghaddam R, Sazvar Z, Javadian N (2021) Designing a sustainable-resilient disaster waste management system under hybrid uncertainty: a case study. Eng Appl Artif Intell 106:104459
Mondal A, Giri BK, Roy SK (2023) An integrated sustainable bio-fuel and bio-energy supply chain: a novel approach based on DEMATEL and fuzzy-random robust flexible programming with \(Me\) measure. Appl Energy 343:121225
Mondal A, Roy SK, Zhan J (2023) A reliability-based consensus model and regret theory-based selection process for linguistic hesitant-Z multi-attribute group decision making. Exp Syst Appl 228:120431
Mondal A, Roy SK, Pamucar D (2023) Regret-based three-way decision making with possibility dominance and SPA theory in incomplete information system. Exp Syst Appl 211:118688
Peng X, Yang Y (2017) Algorithms for interval-valued fuzzy soft sets in stochastic multi-criteria decision making based on regret theory and prospect theory with combined weight. Appl Soft Comput 54:415–430
Qian J, Hong C, Yu Y, Liu C, Miao D (2022) Generalized multigranulation sequential three-way decision models for hierarchical classification. Inf Sci 616:66–87
Rezazadeh J, Bagheri R, Karimi S, Nazarian-Jashnabadi J, Zahedian Nezhad M (2023) Examining the Impact of Product Innovation and Pricing Capability on them International Performance of Exporting Companies with the Mediating Role of Competitive Advantage for Analysis and decision making. J Oper Intell 1(1):30–43. https://doi.org/10.31181/jopi1120232
Sun B, Ma W, Li B, Li X (2018) Three-way decisions approach to multiple attribute group decision making with linguistic information-based decision-theoretic rough fuzzy set. Int J Approx Reason 93:424–442
Tversky A, Kahneman D (1992) Advances in prospect theory: cumulative representation of uncertainty. J Risk Uncertainty 5(4):297–323
Wang T, Li H, Zhou X, Huang B, Zhu H (2020) A prospect theory-based three-way decision model. Knowl Based Syst 203:106129
Wang T, Li H, Zhang L, Zhou X, Huang B (2020) A three-way decision model based on cumulative prospect theory. Inf Sci 519:74–92
Wang T, Li H, Qian Y, Huang B, Zhou X (2020) A regret-based three-way decision model under interval type-2 fuzzy environment. IEEE Trans Fuzzy Syst 30(1):175–189
Wang W, Zhan J, Ding W, Wan S (2023) A three-way decision method with tolerance dominance relations in decision information systems. Artif Intell Rev 56:6403–6438
Xu Y, Liu S, Wang J, Shang X (2022) A novel two-stage TOPSIS approach based on interval-valued probabilistic linguistic \(q\)-rung orthopair fuzzy sets with its application to MAGDM problems. Eng Appl Artif Intell 116:105413
Yager RR (2013) Pythagorean membership grades in multicriteria decision making. IEEE Trans Fuzzy Syst 22(4):958–965
Yager RR (2016) Generalized orthopair fuzzy sets. IEEE Trans Fuzzy Syst 25(5):1222–1230
Yao Y (2010) Three-way decisions with probabilistic rough sets. Inf Sci 180(3):341–353
Younis Al-Zibaree HK, Konur M (2023) Fuzzy Analytic Hierarchal Process for Sustainable Public Transport System. J Oper Intell 1(1):1–10. https://doi.org/10.31181/jopi1120234
Zhan J, Ye J, Ding W, Liu P (2021) A novel three-way decision model based on utility theory in incomplete fuzzy decision systems. IEEE Trans Fuzzy Syst 30(7):2210–2226
Zhang X, Wang J (2023) \(Q\)-rung interval-valued probabilistic dual hesitant fuzzy sets: a new tool for multiattribute group decision-making. Math Probl Eng. https://doi.org/10.1155/2023/9749711
Zheng Q, Liu X, Wang W, Wu Q, Deveci M, Pamucar D (2023) The integrated prospect theory with consensus model for risk analysis of human error factors in the clinical use of medical devices. Exp Syst Appl 217:119507
Zhu J, Ma X, Zhan J, Yao Y (2022) A three-way multi-attribute decision making method based on regret theory and its application to medical data in fuzzy environments. Appl Soft Comput 123:108975
Zhu J, Ma X, Kou G, Herrera-Viedma E, Zhan J (2023) A three-way consensus model with regret theory under the framework of probabilistic linguistic term sets. Inf Fusion 95:250–274
Acknowledgements
The author Binoy Krishna Giri is very much grateful to the University Grant Commission of India for supporting financially to continue this research work under JRF (UGC) scheme: Sanctioned letter number [F.NO. 16-9(June 2019)/2019(NET/CSIR)].
Funding
This work is supported by the University Grant Commission of India to continue this research work under JRF (UGC) scheme: Sanctioned letter number [F.NO. 16-9(June 2019)/2019(NET/CSIR)].
Author information
Authors and Affiliations
Contributions
All authors are equally contributed to this study.
Corresponding author
Ethics declarations
Competing interest
The authors affirm that they have no known financial or interpersonal conflicts that may influence the research presented in this study.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Giri, B.K., Roy, S.K. & Deveci, M. Projection based regret theory on three-way decision model in probabilistic interval-valued q-rung orthopair hesitant fuzzy set and its application to medicine company. Artif Intell Rev 56 (Suppl 3), 3617–3649 (2023). https://doi.org/10.1007/s10462-023-10611-3
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10462-023-10611-3