Abstract
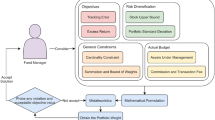
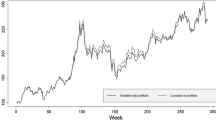
Index tracking consists in reproducing the performance of a stock-market index by investing in a subset of the stocks included in the index. A hybrid strategy that combines an evolutionary algorithm with quadratic programming is designed to solve this NP-hard problem: Given a subset of assets, quadratic programming yields the optimal tracking portfolio that invests only in the selected assets. The combinatorial problem of identifying the appropriate assets is solved by a genetic algorithm that uses the output of the quadratic optimization as fitness function. This hybrid approach allows the identification of quasi-optimal tracking portfolios at a reduced computational cost.
Similar content being viewed by others
References
Alexander, C. (1999). Optimal hedging using cointegration. Philosophical Transactions of the Royal Society of London. Series A. Mathematical, Physical and Engineering Sciences, 357(1758), 2039–2058.
Ammann, M., & Zimmermann, H. (2001). Tracking error and tactical asset allocation. Financial Analysts Journal, 57(2), 32–43.
Beasley, J. E. (1990). OR-Library: distributing test problems by electronic mail. Journal of the Operational Research Society, 41(11), 1069–1072.
Beasley, J. E., Meade, N., & Chang, T. J. (2003). An evolutionary heuristic for the index tracking problem. European Journal of Operations Research, 148(3), 621–643.
Buckley, I. R. C., & Korn, R. (1998). Optimal index tracking under transaction costs and impulse control. International Journal of Theoretical and Applied Finance, 1(3), 315–330.
Consiglio, A., & Zenios, S. A. (2001). Integrated simulation and optimization models for tracking international fixed-income indices. Mathematical Programming, 89(2), 311–339.
Gilli, M., & Këllezi, E. (2001). Threshold accepting for index tracking. Computing in economics and finance (Vol. 72). Society for Computational Economics.
Holland, J. (1975). Adaptation in natural and artificial systems. Ann Arbor: The University of Michigan Press.
Lobo, M., Fazel, M., & Boyd, S. (2007). Portfolio optimization with linear and fixed transaction costs. Annals of Operations Research, 152(1), 341–365. doi:10.1007/s10479-006-0145-1.
Markowitz, H. (1987). Mean-variance analysis in portfolio choice and capital markets. Cambridge: Basil Blackwell.
Moral-Escudero, R., Ruiz-Torrubiano, R., & Suarez, A. (2006). Selection of optimal investment portfolios with cardinality constraints. In Proceedings of the IEEE congress on evolutionary computation 2006 (pp. 2382–2388), 16–21 July 2006.
Radcliffe, N. (1992). Genetic set recombination. In L. Darrell Whitley (Ed.), Foundations of genetic algorithms (Vol. 2). San Mateo: Morgan Kaufmann.
Rudolf, M., Wolter, H., & Zimmermann, H. (1999). A linear model for tracking error minimization. Journal of Banking and Finance, 23(1), 85–103.
Shapcott, J. (1992). Index tracking: genetic algorithms for investment portfolio selection (Technical report, EPCC-SS92-24). Edinburgh, Parallel Computing Centre.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Ruiz-Torrubiano, R., Suárez, A. A hybrid optimization approach to index tracking. Ann Oper Res 166, 57–71 (2009). https://doi.org/10.1007/s10479-008-0404-4
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10479-008-0404-4