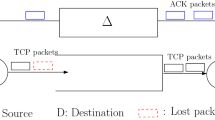
Abstract
We approximate the distribution of the TCP-flow rate by deriving it from the joint bivariate distribution of the flow sizes and flow durations of a given access network. The latter distribution is represented by a bivariate extreme value distribution using the Pickand’s dependence A-function. We estimate the A-function to measure the dependencies of random pairs: TCP-flow size and duration, the rate of TCP-flow and size, as well as the rate and duration. We provide a method to test that the achieved estimate of A-function is good and perform the analysis with one concrete data example.
Similar content being viewed by others
References
Beirlant, J., Goegebeur, Y., Teugels, J., & Segers, J. (2004). Statistics of extremes. New York: Wiley.
Brockwell, P., & Davis, R. (1991). Time series: theory and methods. Berlin: Springer.
Capéraà, P., Fougères, A.-L., & Genest, C. (1997). Estimation of bivariate extreme value copulas. Biometrika, 84, 567–577.
Castellana, J. V., & Leadbetter, M. R. (1986). On smoothed probability density estimation for stationary processes. Stochastic Processes and their Applications, 21, 179–193.
Coles, S. (2001). An introduction to statistical modeling of extreme values. Berlin: Springer.
D’Auria, B., & Resnick, S. (2006). Data network models of burstiness. Advances in Applied Probability, 38, 373–404.
Davis, R., & Resnick, S. (1985). Limit theory for moving averages of random variables with regularly varying tail probabilities. Annals of Probability, 13, 179–195.
Davydov, Y., Paulauskas, V., & Račkauskas, A. (2000). More on p-stable convex sets in Banach spaces. Journal of Theoretical Probability, 13(1), 39–64.
Embrechts, P., Klüppelberg, C., & Mikosch, T. (1997). Modelling extremal events for finance and insurance. Berlin: Springer.
Fougères, A.-L. (2004). Multivariate extremes. In Extreme values in finance, telecommunications and the environment (pp. 373–388). London: Chapman & Hall.
Hall, P., & Tajvidi, N. (2000). Distribution and dependence-function estimation for bivariate extreme-value distributions. Bernoulli, 6, 835–844.
Hall, P., Lahiri, S. N., & Truong, Y. K. (1995). On bandwidth choice for density estimation with dependent data. Annals of Statistics, 23(6), 2241–2263.
Kendall, M. (1970). Rank correlation methods (4th edn.). London: Griffin.
Kettani, H., & Gubner, J. A. (2006). A novel approach to the estimation of the long-range dependence parameter. IEEE Transactions on Circuits and Systems-II: Express Briefs, 53(6), 463–467
Kilpi, J., & Lassila, P. (2006). Micro- and macroscopic analysis of RTT variability in GPRS and UMTS networks. In F. Boavida (Eds.), LNCS: Vol. 3976. Networking 2006 (pp. 1176–1181). Berlin: Springer.
Leadbetter, M. R. (1983). Extremes and local dependence in stationary sequences. Probability Theory and Related Fields, 65(2), 291–306.
Markovich, N. M. (2005). On-line estimation of the tail index for heavy-tailed distributions with applications to WWW-traffic. In Proceedings of the EuroNGI first conference on NGI: traffic engineering, Rome, Italy.
Markovitch, N. M., & Krieger, U. R. (2002). The estimation of heavy-tailed probability density functions, their mixtures and quantiles. Computer Networks, 40(3), 459–474.
Markovich, N. M., & Krieger, U. R. (2006). Inspection and analysis techniques for traffic data arising from the Internet. In Proceedings of the HETNETs’04 2nd international working conference on performance modelling and evaluation of heterogeneous networks, Ilkley, West Yorkshire (pp. 72/1–72/9).
Mikosch, T. (2002). Modeling dependence and tails of financial time series (Technical Report Working Paper No. 181). University of Copenhagen, Laboratory of Actuarial Mathematics.
Resnick, S. (1997). Heavy tail modeling and teletraffic data. Annals of Statistics, 25, 1805–1869. With discussion and a rejoinder by the author.
Resnick, S. (2006). Heavy-tail phenomena. Probabilistic and statistical modeling. Berlin: Springer.
Ribatet, M. (2006). A user’s guide to the POT package (Version 1.0).
Taqqu, M., & Teverovsky, V. (1998). On estimating the intensity of long-range dependence in finite and infinite variance time series. In R. J. Adler, F. E. Feldman, & M. S. Taqqu (Eds.), A practical guide to heavy tails (pp. 177–217). Basel: Birkhäuser.
Tstat (2007). Tstat: TCP statistic and analysis tool. http://tstat.tlc.polito.it/.
van de Meent, R., & Mandjes, M. (2005). Evaluation of ‘user-oriented’ and ‘black-box’ traffic models for link provisioning. In Proceedings of the 1st EuroNGI conference on next generation Internet networks traffic engineering, Rome, Italy. New York: IEEE Press.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Markovich, N.M., Kilpi, J. Bivariate statistical analysis of TCP-flow sizes and durations. Ann Oper Res 170, 199–216 (2009). https://doi.org/10.1007/s10479-009-0531-6
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10479-009-0531-6