The one-warehouse multi-retailer problem: reformulation, classification, and computational results

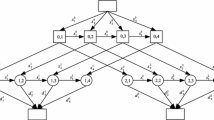
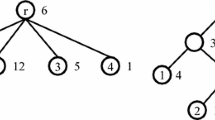
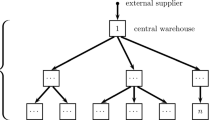
Abstract

We consider the one-warehouse multi-retailer problem where a warehouse replenishes multiple retailers with deterministic dynamic demands over a horizon. The problem is to determine when and how much to order to the warehouse and retailers such that the total system-wide costs are minimized. We propose a new (combined transportation and shortest path based) integer programming reformulation for the problem in addition to the echelon stock and transportation based formulations in the literature. We analyze the strength of the LP relaxations of three formulations and show that the new formulation is stronger than others. We also show that the new and transportation based formulations are equivalent for the joint replenishment problem, where the warehouse is a crossdocking facility. We extend all formulations to the case with initial inventory at the warehouse and reveal the relation among their LP relaxations. We present our computational experiments with all formulations over a set of randomly generated test instances.

Appendix

1.1 A.1 Details of proof of Theorem 1

We show that (X,y) constructed using (39) belongs to F(SES) as follows:

• (a) Constraints (9): For 1≤i≤N,1≤k≤T, (16) is equivalent to (9). For i=0, 1≤k≤T, we sum (14) over all i and t and modify the summation bounds since q≤t≤k, which gives

  $$\sum_{i=1}^{N}\sum_{t=1}^{k}\sum_{q=1}^{t}{W_{iqtk}} =\sum_{q=1}^{k}\sum_{i=1}^{N}\sum_{t=q}^{k}{W_{iqtk}} =\sum_{i=1}^{N}\sum_{t=1}^{k}{X_{itk}},\quad 1 \leq k \leq T.$$

  The term in the right-hand side above is equal to d _0k ($=\sum_{i=1}^{N}{d_{ik}}$) due to (16). Substituting X _0qk in place of $\sum_{i=1}^{N}\sum_{t=q}^{k}{W_{iqtk}}$ due to (39) gives

  $$\sum_{q=1}^{k}{X_{0qk}}=d_{0k},\quad 1 \leq k \leq T,$$

  which is equivalent to (9) for i=0,1≤k≤T. Thus, constraints (9) hold.

• (b) Constraints (10): For 1≤i≤N,1≤t≤k≤T, (17) is equivalent to (10). For i=0,1≤t≤k≤T, we sum (15) over all i, which gives

  $$\sum_{i=1}^{N}\sum_{t=q}^{k}{W_{iqtk}} \leq \Biggl(\sum_{i=1}^{N}{d_{ik}}\Biggr)y_{0q} =d_{0k}y_{0q},\quad 1 \leq q \leq k \leq T.$$

  Substituting X _0qk in place of $\sum_{i=1}^{N}\sum_{t=q}^{k}{W_{iqtk}}$ due to (39) gives

  $$X_{0qk} \leq d_{0k}y_{0q},\quad 1 \leq q \leq k \leq T,$$

  which is equivalent to (10) for i=0,1≤q≤k≤T. Thus, constraints (10) hold.

• (c) Constraints (11): Summing (14) over t (from r=1 to t) and all i and k, we obtain

  $$\sum_{i=1}^{N}\sum_{r=1}^{t}\sum_{k=r}^{T}\sum_{q=1}^{r}{W_{iqrk}} =\sum_{i=1}^{N}\sum_{r=1}^{t}\sum_{k=r}^{T}{X_{irk}},\quad 1 \leq t \leq T.$$

  Since q≤r≤t, we can rewrite the above equation as

  $$\sum_{i=1}^{N}\sum_{q=1}^{t}\sum_{r=q}^{t}\sum_{k=r}^{T}{W_{iqrk}} =\sum_{i=1}^{N}\sum_{r=1}^{t}\sum_{k=r}^{T}{X_{irk}},\quad 1 \leq t \leq T.$$

  Adding a term to both sides, we have

  

  The left-hand side of the above equation reduces to

  $$\sum_{i=1}^{N}\sum_{q=1}^{t}\sum_{r=q}^{T}\sum_{k=r}^{T}{W_{iqrk}} =\sum_{i=1}^{N}\sum_{q=1}^{t}\sum_{k=q}^{T}\sum_{r=q}^{k}{W_{iqrk}},\quad 1 \leq t \leq T,$$

  which is indeed equal to $\sum_{q=1}^{t}\sum_{k=q}^{T}{X_{0qk}}$ due to (39). Thus, it becomes

  $$\sum_{q=1}^{t}\sum_{k=q}^{T}{X_{0qk}} = \sum_{i=1}^{N}\sum_{r=1}^{t}\sum_{k=r}^{T}{X_{irk}} + \sum_{i=1}^{N}\sum_{q=1}^{t}\sum_{r=t+1}^{T}\sum_{k=r}^{T}{W_{iqrk}},\quad 1 \leq t \leq T,$$

  which ensures that

  $$\sum_{r=1}^{t}\sum_{k=r}^{T}{X_{0rk}}\geq \sum_{i=1}^{N}\sum_{r=1}^{t}\sum_{k=r}^{T}{X_{irk}},\quad 1 \leq t \leq T.$$

  Thus, constraints (11) hold.

• (d) To show that φ _SES (X,y)=φ _TP (W,X,y) for (X,y)∈F(SES) and (W,X,y)∈F(TP), we express φ _TP (W,X,y) in terms of

  

  Let the second term of the above expression be equal to

  $$\sum_{i=1}^{N}\sum_{q=1}^{T}\sum_{t=q}^{T}\sum_{k=t}^{T}\Biggl(p_{0q}+\sum_{l=q}^{k-1}{h_{0l}}\Biggr)W_{iqtk} - \sum_{i=1}^{N}\sum_{q=1}^{T}\sum_{t=q}^{T}\sum_{k=t}^{T}\Biggl(\sum_{l=t}^{k-1}{h_{0l}}\Biggr)W_{iqtk}.$$

  Since q≤t≤k we can modify the summation bounds and we obtain

  

  Using (39) for the first term and (14) for the second term above, we obtain

  $$\sum_{q=1}^{T}\sum_{k=q}^{T}{H_{0qk}X_{0qk}} -\sum_{i=1}^{N}\sum_{t=1}^{T}\sum_{k=t}^{T}\Biggl(\sum_{l=t}^{k-1}{h_{0l}}\Biggr)X_{itk}.$$

  Then, replacing the above with the second term of φ _TP (W,X,y), φ _TP (W,X,y) becomes

  

  which is equal to φ _SES (X,y).

1.2 A.2 Details of proof of Theorem 2

We show that (W,X,y) constructed using (40) and (41) belongs to F(TP) as follows:

• (a) Constraints (14): Summing (26) over k (from j=k and j=T) and multiplying both sides by d _ik , we obtain

  $$\sum_{q=1}^{t}d_{ik}\sum_{j=k}^{T}{U_{iqtj}} = d_{ik}\sum_{j=k}^{T}{Z_{itj}},\quad 1 \leq i \leq N,1 \leq t \leq k \leq T.$$

  Substituting (40) and (41) into the above equation gives

  $$\sum_{q=1}^{t}{W_{iqtk}}=X_{itk},\quad 1 \leq i \leq N,1 \leq t \leq k \leq T,$$

  which is equivalent to (14). Thus, constraints (14) hold.

• (b) Constraints (15): Note that (41) can be rewritten as $W_{iqtk}=d_{ik}\sum_{j=k}^{T}{a_{itj}U_{iqtj}}$ since a _itj =1 for t≤k≤j≤T if d _ik >0, otherwise W _iqtk becomes zero. Then, we substitute W _iqkt /d _it in place of $\sum_{r=t}^{T}{a_{ikr}U_{iqkr}}$ in (27), which gives

  $$\sum_{k=q}^{t}{(W_{iqkt}/d_{it})} \leq y_{0q},\quad 1 \leq i \leq N,1 \leq q \leq t \leq T.$$

  Thus, constraints (15) hold.

• (c) Constraints (16): Summing (28) and (29) from t=2 to t=k, we obtain

  $$\sum_{r=1}^{k}\sum_{j=k}^{T}{Z_{irj}} = 1,\quad 1 \leq i \leq N,1 \leq k \leq T.$$

  Substituting X _irk /d _ik in place of $\sum_{j=k}^{T}{Z_{irj}}$ due to (40) gives

  $$\sum_{r=1}^{k}{(X_{irk}/d_{ik})} = 1,\quad 1 \leq i \leq N,1 \leq k \leq T,$$

  which is equivalent to (16). Thus, constraints (16) hold.

• (d) Constraints (17): Note that (30) can be rewritten as

  $$\sum_{j=k}^{T}{a_{itj}Z_{itj}} \leq y_{it},\quad 1 \leq i \leq N,1 \leq t \leq k \leq T, $$

  (59)

  which actually encompasses (30). Equation (40) can be rewritten as $X_{itk}=d_{ik}\sum_{j=k}^{T}{a_{itj}Z_{itj}}$, as done for W variables in part (b). Substituting X _itk /d _ik in place of $\sum_{j=k}^{T}{a_{itj}Z_{itj}}$ in (59) gives

  $$(X_{itk}/d_{ik}) \leq y_{it},\quad 1 \leq i \leq N,\ 1 \leq t \leq k \leq T,$$

  which is equivalent to (17). Thus, constraints (17) hold.

• (e) To show that φ _TP (W,X,y)=φ _SP (U,Z,y) for (W,X,y)∈F(TP) and (U,Z,y)∈F(SP), we express φ _TP (W,X,y) in terms of

  $$\sum_{i=0}^{N}\sum_{t=1}^{T}{f_{it}y_{it}} + \sum_{i=1}^{N}\sum_{q=1}^{T}\sum_{t=q}^{T}\sum_{k=t}^{T}{H'_{0qt}W_{iqtk}} + \sum_{i=1}^{N}\sum_{t=1}^{T}\sum_{k=t}^{T}{H'_{itk}X_{itk}}.$$

  Substituting (40) and (41) into φ _TP (W,X,y), we obtain

  

  (60)

  We can rewrite the second term in (60) as

  

  (61)

  We can rewrite the third term in (60) as

  $$\sum_{i=1}^{N}\sum_{t=1}^{T}\sum_{k=t}^{T}\Biggl(\Biggl(p_{it}d_{ik}+\sum_{l=t}^{k-1}{h_{il}d_{ik}}\Biggr)\sum_{j=k}^{T}Z_{itj}\Biggr),$$

  which is equal to

  

  (62)

  Thus, summing the first term in (60), (61), and (62), we obtain

  $$\sum_{i=0}^{N}\sum_{t=1}^{T}{f_{it}y_{it}}+ \sum_{i=1}^{N}\sum_{t=1}^{T}\sum_{k=t}^{T}\sum_{q=1}^{t}{H'_{0qt} D_{itk}U_{iqtk}} +\sum_{i=1}^{N}\sum_{t=1}^{T}\sum_{k=t}^{T}{G_{itk}Z_{itk}},$$

  which is equal to φ _SP (U,Z,y).

1.3 A.3 Details of proof of Theorem 3

To show that $\varphi_{\mathit{TP\hbox{-}JRP}}{(X,y)} =\varphi_{\mathit{SP\hbox{-}JRP}}{(Z,y)}$ for any $(X,y)\in F(\mathit{TP\hbox{-}JRP})$ and the associated (Z,y) $\in F(\mathit{SP\hbox{-}JRP})$ or vice versa, we consider

$$\varphi_{\mathit{TP\hbox{-}JRP}}{(X,y)} = \sum_{i=0}^{N}\sum_{t=1}^{T}{f_{it}y_{it}} +\sum_{i=1}^{N}\sum_{t=1}^{T}\sum_{k=t}^{T}{H'_{itk} X_{itk}},$$

which is equivalent to

$$\sum_{i=0}^{N} \sum_{t=1}^{T}{f_{it}y_{it}} + \sum_{i=1}^{N}\sum_{t=1}^{T}\Biggl[p_{it}d_{it}(X_{itt}/d_{it}) + \sum_{k=t+1}^{T}\Biggl(p_{it}+\sum_{l=t}^{k-1}h_{il}\Biggr)d_{ik}(X_{itk}/d_{ik})\Biggr].$$

We can insert V _itk in place of X _itk /d _ik above regardless of the value of d _ik since by definition V _itk =X _itk /d _ik if d _ik >0, and $(p_{it}+\sum_{l=t}^{k-1}{h_{il}})d_{ik}V_{itk}=0$ if d _ik =0 (also p _it d _it V _itt =0 if d _it =0). So we have

$$\sum_{i=0}^{N}\sum_{t=1}^{T}{f_{it}y_{it}} + \sum_{i=1}^{N}\sum_{t=1}^{T}\Biggl[p_{it}d_{it}(V_{itt})+\sum_{k=t+1}^{T}\Biggl(p_{it}+\sum_{l=t}^{k-1}h_{il}\Biggr)d_{ik}(V_{itk})\Biggr].$$

Since d _ik =D _itk −D _it,k−1 for t≤k−1, $\sum_{k=t+1}^{T}(p_{it}+\sum_{l=t}^{k-1}h_{il})d_{ik}(V_{itk})$ equals to

Thus,

$$\varphi_{\mathit{TP\hbox{-}JRP}}{(X,y)} = \sum_{i=0}^{N}\sum_{t=1}^{T}{f_{it}y_{it}} +\sum_{i=1}^{N}\sum_{t=1}^{T}\Biggl[G_{itt}V_{itt}+\sum_{k=t+1}^{T}(G_{itk}-G_{it,k-1})V_{itk}\Biggr].$$

Rewriting the second term of the right-hand side of above equation, we obtain

$$\sum_{i=0}^{N}\sum_{t=1}^{T}{f_{it}y_{it}} + \sum_{i=1}^{N}\sum_{t=1}^{T}\Biggl[\sum_{k=t}^{T-1}G_{itk}(V_{itk}-V_{it,k+1})+G_{itT}V_{itT}\Biggr].$$

Inserting Z variables using (45) and (46) to the above expression gives

$$\sum_{i=0}^{N}\sum_{t=1}^{T}{f_{it}y_{it}} + \sum_{i=1}^{N}\sum_{t=1}^{T}\sum_{k=t}^{T}{G_{itk}Z_{itk}},$$

which is $\varphi_{\mathit{SP\hbox{-}JRP}}{(Z,y)}$.

1.4 A.4 Details of proof of Theorem 4

We show that (W,X,y) constructed using (57) and (58) belongs to $F(\mathit{TP\hbox{-}I})$ as follows:

• (a) Constraints (15)–(17): They are already shown to be feasible in Theorem 2.

• (b) Constraints (50): Summing (54) over k (from j=k to j=T) and multiplying both sides by d _ik , we obtain

  $$\sum_{q=1}^{t}d_{ik}\sum_{j=k}^{T}{U_{iqtj}}+d_{ik}\sum_{j=k}^{T}{U_{i0tj}} =d_{ik}\sum_{j=k}^{T}{Z_{itj}},\quad 1 \leq i \leq N,1 \leq t \leq k \leq T.$$

  Substituting (57) and (58) into the above equation gives

  $$\sum_{q=1}^{t}{W_{iqtk}}+W_{i0tk}=X_{itk},\quad 1 \leq i \leq N,1 \leq t \leq k \leq T,$$

  which is (50). Thus, constraints (50) hold.

• (c) Constraint (51): (55) is

  $$\sum_{i=1}^{N}\sum_{t=1}^{T}\sum_{k=t}^{T}{D_{itk}U_{i0tk}} =\sum_{i=1}^{N}\sum_{t=1}^{T}\sum_{k=t}^{T}{(d_{it}+d_{i,t+1}+\cdots +d_{ik})U_{i0tk}} \leq I'_{00}.$$

  The above inequality can be rewritten as

  

  Substituting (58) for q=0 into the above expression gives

  $$\sum_{i=1}^{N}\sum_{t=1}^{T}\sum_{k=t}^{T}{W_{i0tk}} \leq I'_{00}.$$

  Thus, constraint (51) holds.

• (d) To show that $\varphi_{\mathit{TP\hbox{-}I}}{(W,X,y)} =\varphi_{\mathit{SP\hbox{-}I}}{(U,Z,y)}$ for $(W,X,y)\in F(\mathit{TP\hbox{-}I})$ and $(U,Z,y)\in F(\mathit{SP\hbox{-}I})$, we express $\varphi_{\mathit{TP\hbox{-}I}}{(W,X,y)}$ in terms of

  $$\varphi_{TP}{(W,X,y)}+\sum_{r=1}^{T}{h_{0r}I'_{00}} - \sum_{i=1}^{N}\sum_{t=1}^{T}\sum_{k=t}^{T} \Biggl(\sum_{r=t}^{T}h_{0r}\Biggr)W_{i0tk}.$$

  From Theorem 2, φ _TP (W,X,y)=φ _SP (U,Z,y), i.e.,

  

  Since D _itk U _i0tk =W _i0tk as shown in part (c) above, $\varphi_{\mathit{TP\hbox{-}I}}{(W,X,y)}$ can be rewritten as

  $$\varphi_{\mathit{SP}}{(U,Z,y)}+\sum_{r=1}^{T}{h_{0r}I'_{00}} - \sum_{i=1}^{N}\sum_{t=1}^{T}\sum_{k=t}^{T} \Biggl(\sum_{r=t}^{T}h_{0r}\Biggr)D_{itk}U_{i0tk},$$

  which is equal to $\varphi_{\mathit{SP\hbox{-}I}}{(U,Z,y)}$.