Martingale methods for pricing inventory penalties under continuous replenishment and compound renewal demands

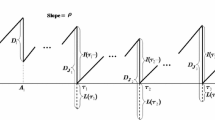
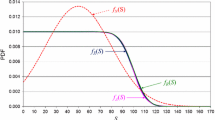
Abstract

This paper addresses the problem of inventory penalty pricing under the risk-neutral valuation principle. The underlying production-inventory system has a constant replenishment rate and a compound renewal demand stream (i.e., iid demand interarrival times are independent of iid demand sizes), and is subject to underage and overage penalties. Our pricing approach treats the penalties as a series of perpetual American options, and constructs auxiliary martingale processes in term of the inventory process. We provide a necessary and sufficient martingale condition for general compound renewal demands. Explicit expressions of penalty functions for underage and overage are obtained for the case where demand arrivals follow a Poisson process.

Appendix

Proof of Lemma 1

Substituting Eq. (3.1) into Eq. (2.10) and noting that I(t) and M(t) determine each other for each t, we rewrite the left hand side of Eq. (2.6) for any 0≤i≤j as

(8.1)

For the embedded martingale condition to hold, it is necessary and sufficient that the right-most side of Eq. (8.1) be equal to M(A _i ), which is equivalent to the condition

Equation (3.3) now readily follows, since $\tilde{f}_{T}(r - c \rho)\tilde{f}_{D}(c)$ is non-negative. □

Proof of Lemma 2

To prove part (a), we show that the derivatives of l _T (c) satisfy

(8.2)

(8.3)

Equation (8.2) follows from the facts

(8.4)

(8.5)

where Eq. (8.4) is an immediate consequence of the Laplace transform, and Eq. (8.5) follows by the Leibniz integral rule.

To prove (8.3), note that the denominator is positive, so it remains to show that the numerator is positive too. Differentiating Eq. (8.5) with the aid of the Leibniz integral rule yields

(8.6)

Substituting (8.4), (8.5) and (8.6) into the numerator of Eq. (8.3), the latter becomes

(8.7)

Finally, applying the Cauchy-Schwarz inequality (Karr 1993) to the product of expectations in the first term of Eq. (8.7) results in the inequality,

(8.8)

where the strict inequality follows from the fact that the random variables on the left-hand side above are not proportional to each other. Equation (8.8) establishes that the numerator of Eq. (8.3) is positive, thereby completing the proof of part (a).

To prove part (b), we apply an argument similar to that for part (a). Accordingly, we show that the derivatives of l _D (c) satisfy

(8.9)

(8.10)

Equation (8.9) follows from the facts

(8.11)

(8.12)

where Eq. (8.11) is an immediate consequence of the Laplace transform, and Eq. (8.12) follows by the Leibniz integral rule.

To prove Eq. (8.10), note that the denominator is positive, so it remains to show that the numerator is positive too. Differentiating Eq. (8.12) with the aid of the Leibniz integral rule yields,

(8.13)

Substituting Eqs. (8.11), (8.12) and (8.13) into the numerator of Eq. (8.10), the latter becomes

(8.14)

Finally, applying the Cauchy-Schwarz inequality to the first term of Eq. (8.14) results in the inequality,

(8.15)

where the strict inequality follows from the fact that the random variables on the left-hand side above are not proportional to each other. Equation (8.15) establishes that the numerator of Eq. (8.10) is positive, thereby completing the proof of part (b). □

Proof of Proposition 3

Let D denote a generic exponential demand size with pdf f _D (x)=βe ^−βx,β>0. By Lemma 3 we can write

(8.16)

where the second equality follows from the memorylessness of the exponential distribution.

Define the functions

(8.17)

and

(8.18)

Next, we rewrite Eq. (8.17) as

(8.19)

where the first equality holds by the chain rule of conditional probabilities,

and the second equality follows from Eq. (8.16) combined with the fact that $f_{L(\tau _{1}^{(0)})| I(\tau _{1}^{(0)} - ),\tau _{1}^{(0)}, I(0)} = f_{L(\tau _{1}^{(0)})| I(\tau _{1}^{(0)} - )}$. In view of Eqs. (8.18) and (8.19), we now have

(8.20)

Furthermore, integrating both sides of Eq. (8.18) with respect to x from zero to infinity, we get

(8.21)

Next, we write

(8.22)

Here, the first equality follows from the fact that $L(\tau_{1}^{(0)}) =- I(\tau_{1}^{(0)})$, the second and third equality hold by definition, the fourth equality holds by Eq. (8.20), the fifth equality follows from (8.21), and the sixth equality is a consequence of exponentially distributed demand sizes. Finally, the above equation equals $e^{c_{1}u}$ by Eq. (5.4), which completes the proof. □