Impact of taxation on international transfer pricing and offshoring decisions

Abstract

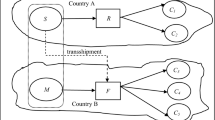
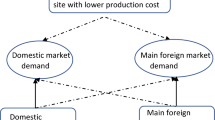
A multinational company may move production to a foreign country to take advantage of low manufacturing cost, and/or experience tax savings. Transfer prices play an important and strategic role on income shifting by multinational companies. In this paper, we construct a framework for optimal decision making in global supply chains with uncertain and price-dependent demand, propose methods to improve global supply chain parties’ performance, and explore schemes to integrate global supply chains. The optimal pricing and offshoring decisions are investigated for different situations where the low foreign production cost and low foreign tax rate exist or only one of them is available. The case of low foreign tax rate without the advantage of low foreign production cost provides the most interesting findings that partial offshoring dominates when a certain threshold is met. In addition, the double marginalization is examined in decentralized global supply chains similar to the mechanism in newsvendor problems. Due to the existence of the tax jurisdiction, the double marginalization cannot be completely eliminated by coordinating schemes. Finally, the traditional buy back contract is found to be unable to coordinate global supply chains, while a modified sales sharing contract can improve the performance of the global supply chain.

Appendix

Proof of Theorem 1

Consider the first partial derivatives of π(P,T,z) taken with respect to T: $\frac{\partial\pi}{\partial T} = y(P)z(t_{L} - t_{F})$. The function is monotone increasing in T when t _L >t _F and monotone decreasing in T when t _L <t _F . Following the sequential procedure in Petruzzi and Dada (1999), we have $T_{c}^{*} = T_{U}$ when t _L >t _F , and $T_{c}^{*} = c_{F}$ if t _L <t _F . In addition, any feasible transfer price T is optimal when t _L =t _F . We have three cases as follows.

Case 1 t _L >t _F . Substitute $T_{c}^{*} = T_{U}$ into the profit function, we have,

$$\begin{aligned} \frac{\partial\pi(T_{c}^{*},P,z)}{\partial P} &= \frac{y(P)}{P} \bigl\{ (1 - t_{L}) \bigl[ ( - b + 1)Pz + bzT_{U} + (b - 1)P\varLambda(z) \bigr] \\ &\quad {} - (1 - t_{F})bz(T_{U} - c_{F}) \bigr\} \end{aligned}$$

Let

$$\begin{aligned} P_{c}^{*} = \frac{bz}{(b - 1)(z - \varLambda(z))}\frac{(1 - t_{L})T_{U} - (1 - t_{F})(T_{U} - c_{F})}{1 - t_{L}}, \end{aligned}$$

it is easy to see that $\frac{\partial\pi(T_{c}^{*},P,z)}{\partial P} < 0\ \forall P > P_{c}^{*}$ and $\frac{\partial\pi(T_{c}^{*},P,z)}{\partial P} < 0\ \forall P < P_{c}^{*}$, thus $P_{c}^{*}$ is the unique maximum of $\pi (T_{c}^{*},P,z)$ given z. If we define $M \equiv\frac{(1 - t_{L})T_{U} - (1 - t_{F})(T_{U} - c_{F})}{1 - t_{L}}$, the optimal retail price can be expressed as $P_{c}^{*} = \frac{bzM}{(b - 1)(z - \varLambda(z))}$.

Following the tax regulation, we should examine if the suggested optimal retail price and transfer price make the local company a non-negative profit. In fact, we have the following the following profit function of the local company via substituting $P_{c}^{*}$ and $T_{c}^{*}$ into Eq. (1),

$$\pi_{L} = \frac{y(P)z}{(b - 1)(1 - t_{L})} \bigl\{ T_{U} \bigl[ (1 - t_{L}) - b(1 - t_{F}) \bigr] + bc_{F}(1 - t_{F}) \bigr\} $$

Therefore, as long as $T_{U} \le\frac{bc_{F}(1 - t_{F})}{b(1 - t_{F}) - (1 - t_{L})}$, the non-negativity of local profit can be guaranteed. In the case that the transfer price has a high upper limit, the company should sacrifice partial of the tax benefit and set the ultimate transfer price to be threshold, i.e., $T_{c}^{*} = \frac{bc_{F}(1 - t_{F})}{b(1 - t_{F}) - (1 - t_{L})}$. For the ease of future expression, in the notation M, we declare that T _U denotes the true upper limit T _U if the inequality is satisfied or the threshold $\frac{bc_{F}(1 - t_{F})}{b(1 - t_{F}) - (1 - t_{L})}$ otherwise.

Furthermore, the transfer price should not be higher than the retail price, i.e., T≤P. Such inequality leads to $T_{c}^{*} \le\frac{Kc_{F}(1 - t_{F})}{K(t_{L} - t_{F}) + (1 - t_{L})}$. Let $T_{ \le P} = \frac{Kc_{F}(1 - t_{F})}{K(t_{L} - t_{F}) + (1 - t_{L})}$, we can show that T _≤P >c _F .

We give out the optimal z as follows. The optimal profit function is

$$\pi\bigl(T_{c}^{*},P_{c}^{*},z\bigr) = (1 - t_{L}) \bigl[ y\bigl(P_{c}^{*}\bigr)z \bigl(P_{c}^{*} - M\bigr) - P_{c}^{*}y \bigl(P_{c}^{*}\bigr)\varLambda(z) \bigr] $$

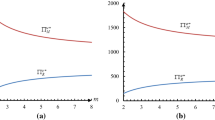
Except the scale (1−t _L ), the structure of $\pi (T_{c}^{*},P_{c}^{*},z)$ is same with that in Theorem 2 of Petruzzi and Dada (1999). Thus, if b≥2 and $r(z) = \frac{\phi(z)}{1 - \varPhi(z)}$ is increasing for A≤z≤B, which implies 2r(z)²+dr(z)/dz>0, there is a unique optimal value $z_{c}^{*}$ which satisfies $\varPhi (z_{c}^{*}) = \frac{z_{c}^{*} + (b - 1)\varLambda(z_{c}^{*})}{bz_{c}^{*}}$.

Case 2 t _L <t _F . $T_{c}^{*} = c_{F}$, $\frac{\partial\pi (T_{c}^{*},P,z)}{\partial P} = (1 - t_{L})\frac{y(P)}{P}[ - (b - 1)P(z - \varLambda(z)) + bzc_{F}]$. Let $P_{c}^{*} = \frac{bzc_{F}}{(b - 1)(z - \varLambda(z))}$, which is the unique maximizer of $\pi(T_{c}^{*},P,z)$ given z. In addition, according to Proposition 2 later, $P_{c}^{*}$ is a qualified retail price which makes the local company owns a positive profit.

Now, we substitute $P_{c}^{*}$ into $\pi(T_{c}^{*},P,z)$ and optimize over z. $\pi(T_{c}^{*},P_{c}^{*},z) = (1 - t_{L}) [ y(P_{c}^{*})z(P_{c}^{*} - c_{F}) - P_{c}^{*}y(P_{c}^{*})\varLambda(z) ]$. We have the same optimal conditions and same optimal solution $z_{c}^{*}$ as that in case 1. □

Proof of Proposition 1

Simply follow the Theorem 2 of Petruzzi and Dada (1999). □

Proof of Theorem 2

Based on Proposition 2, we substitute $P_{d}^{*}(z,T)$ and $z_{d}^{*}$ into π(T), and take the first order condition with respect to T, then we have

$$\frac{\partial\pi(T)}{\partial T} = \bigl\{ \bigl[ t_{L} - t_{F} - b(1 - t_{F}) \bigr]T + bc_{F}(1 - t_{F}) \bigr\} \cdot azK(KT)^{ - (b + 1)} $$

where $K = \frac{bz}{(b - 1)[z - \varLambda(z)]} > 0$, thus azK(KT)^−(b+1)>0 for all feasible values, therefore π is unimodal in T. Considering the transfer price should meet the condition c _F ≤T≤P, we have $T_{d}^{*} = \frac{bc_{F}(1 - t_{F})}{b(1 - t_{F}) - (t_{L} - t_{F})}$ if t _L >t _F . Note that $\frac{bc_{F}(1 - t_{F})}{b(1 - t_{F}) - (t_{L} - t_{F})} \le c_{F}$ if t _L ≤t _F , but we need the transfer price not less than the foreign manufacturing cost, thus $T_{d}^{*} = c_{F}$ if t _L ≤t _F . □

Proof of Theorem 3

Only the proof of (1b) is shown here. According to the proof of Theorem 1, given λ and T, the optimal retail price is in the form of

$$P(\lambda,T) = K \biggl[ \lambda T + (1 - \lambda)c_{L} - \frac{1 - t_{F}}{1 - t_{L}}\lambda(T - c_{F}) \biggr] $$

Then taking the first order condition with respect to T and λ, respectively

$$\begin{aligned} \frac{\partial\pi(T,\lambda)}{\partial T} & = (b - 1)y(P)\lambda (t_{F} - t_{L}) \bigl[ - (K - 1) \bigl(z - \varLambda(z)\bigr) + \varLambda(z) \bigr] > 0,\\ \frac{\partial\pi(T,\lambda)}{\partial\lambda} & = (b - 1)y(P) \bigl[ (1 - t_{L}) (T - c_{L}) - (1 - t_{F}) (T - c_{F}) \bigr] \\ &\quad {}\times \bigl[ - (K - 1) \bigl(z - \varLambda(z)\bigr) + \varLambda(z) \bigr] \end{aligned}$$

Let $Q = \frac{c_{F}(1 - t_{F}) - (1 - t_{L})c_{L}}{t_{L} - t_{F}}$. When t _L >t _F and c _L <c _F , Q>c _F . If T _U ≤Q, $\frac{\partial\pi(\lambda)}{\partial\lambda} < 0$ for any λ≥0. We conclude that no offshoring exists when T _U ≤Q.

On the other side, if T _U >Q, we have $\frac{\partial\pi(\lambda )}{\partial\lambda} |_{\lambda= 0,T > Q} > 0$ which assures that given any T>Q, π(Δλ)>π(λ=0), i.e, a profit jump at λ=0, where Δλ refers to a small value. Note that π(λ=0) denotes the profit from no offshoring.

But the transfer price T can’t be an arbitrary value; It should satisfy another two conditions besides T>Q: (I) π _L (T)≥0 and (II) T≤P. Recall that the retail price is in the form P(λ,T)=K(λT+(1−λ)c _L ). Given any T>Q, lim _λ→0 P(λ,T)=Kc _L . Therefore, if Kc _L >Q, there exists λ>0 and P(λ,T)≥T is satisfied.

The criterion π _L (T)≥0 requests $T \le\frac{(1 - \lambda)(1 - t_{L})c_{L} + \lambda bc_{F}(1 - t_{F})}{\lambda [ b(1 - t_{F}) - (t_{L} - t_{F}) ]}$. Taking into account the total profit increases as T increases, the form of the optimal transfer price must be like

$$T(\lambda) = \frac{(1 - \lambda)(1 - t_{L})c_{L} + \lambda bc_{F}(1 - t_{F})}{\lambda [ b(1 - t_{F}) - (t_{L} - t_{F}) ]} $$

Along with the criterion T(λ)≤P, i.e.,

$$T(\lambda) \le K\frac{(1 - \lambda)(1 - t_{L})c_{L} + \lambda(1 - t_{F})c_{F}}{(1 - t_{L}) + K\lambda(t_{L} - t_{F})}, $$

we can deduct the optimal λ ^∗ if it exists. To be specific,

$$ \bar{a}\lambda^{2} + \bar{b}\lambda+ \bar{c} \ge0 $$

(9)

where

$$\begin{aligned} \bar{a} & = K(b - 1)(1 - t_{F})(1 - t_{L})(c_{F} - c_{L})\\ \bar{b} & = - K(1 - t_{F}) (1 - t_{L})c_{L} + (1 - t_{L})^{2}c_{L} + (Kc_{L} - c_{F})b(1 - t_{L}) (1 - t_{F})\\ \bar{c} & = - c_{L}(1 - t_{L})^{2} \end{aligned}$$

If c _L <c _F and t _L >t _F , we have $\bar{a} > 0$ and $\bar{c} < 0$, thus the shape of the quadratic curve (Eq. (9)) is upward, so if $\frac{ - \bar{b} + \sqrt{\bar{b}^{2} - 4\bar{a}\bar{c}}}{2\bar{a}} \le1$, i.e., Kb−(K+b)≥0, the optimal solution is $\lambda^{*} = \frac{ - \bar{b} + \sqrt{\bar{b}^{2} - 4\bar{a}\bar{c}}}{2\bar{a}}$. □

Proof of Theorem 4

Similar to the proof of Theorem 3 except that the Proposition 3 has to be considered. □

Proof of Discussion 1

Due to the constraint T≤P, we have to explore the optimal solution from two different conditions, i.e., Path A: looking for a best T with an endogenous optimal λ(T), and Path B: looking for a best λ with an endogenous optimal T(λ).

Path A: Based on Proposition 3, substituting $P_{cd}^{*}(z_{cd}^{*})$ and $z_{cd}^{*}$ into π(T,λ), and taking the first order condition with respect to T, we can prove that π is unimodal in T, and

$$ T^{*}(\lambda) = \frac{\lambda bc_{F}(1 - t_{F}) - (1 - \lambda )c_{L}(t_{F} - t_{L})}{\lambda [ b(1 - t_{F}) - (t_{L} - t_{F}) ]} $$

(10)

When t _L >t _F and c _L <c _F , π(T ^∗(λ),λ) is decreasing in λ from the evidence

$$\begin{aligned} & \frac{\partial\pi (T_{cd}^{*}(\lambda),\lambda)}{\partial\lambda}\\ &\quad = a(1 - t_{F}) (c_{L} - c_{F})z_{cd}^{*} \biggl\{ b\frac{bz_{cd}^{*}}{(b - 1)(z_{cd}^{*} - \varLambda (z_{cd}^{*}))}(1 - t_{F})\frac{\lambda(c_{L} - c_{F}) - c_{L}}{bt_{F} - t_{F} - b + t_{L}}\biggr\} ^{ - b} \end{aligned}$$

Note that the constraint Q≤T≤P should be taken into account before constructing the optimal solutions. T≤P is equivalent to the following inequality by simple algebraic derivation:

$$ \tilde{a}\lambda^{2} + \tilde{b}\lambda+ \tilde{c} \ge0 $$

(11)

where

$$\begin{aligned} \tilde{a} & = Kb(1 - t_{F})(c_{F} - c_{L})\\ \tilde{b} & = c_{L}(t_{L} - t_{F}) + b(1 - t_{F}) (Kc_{L} - c_{F})\\ \tilde{c} & = c_{L}(t_{F} - t_{L}) \end{aligned}$$

If c _L <c _F and t _L >t _F , we have $\tilde{a} > 0$ and $\tilde{c} < 0$, thus the shape of the quadratic curve (Eq. (11)) is upward, so the minimal feasible value of λ is optimal, i.e., $\lambda^{*} = \frac{ - \tilde{b} + \sqrt{\tilde{b}^{2} - 4\tilde{a}\tilde{c}}}{2\tilde{a}}$. If T ^∗(λ ^∗)<Q, there is no optimum (due to $\frac{\partial T^{*}(\lambda)}{\partial\lambda} < 0$) from the path A, noticing that

$$T^{*}(\lambda) = \frac{\lambda bc_{F}(1 - t_{F}) - (1 - \lambda)c_{L}(t_{F} - t_{L})}{\lambda [ b(1 - t_{F}) - (t_{L} - t_{F}) ]} $$

increases as λ decreases.

Path B: Similarly, given T, we can easily find the optimal offshoring proportion λ

$$\lambda^{*}(T) = \frac{c_{L} [ (1 - t_{F})(T - c_{F}) - (1 - t_{L})(T - c_{L}) ]}{(T - c_{L}) [ (b - 1)(1 - t_{F})(T - c_{F}) + (1 - t_{L})(T - c_{L}) ]} $$

Again, the optimal solution must meet T≤P, which is equivalent to the following inequality by simple algebraic derivation:

$$ \hat{a}T^{2} + \hat{b}T + \hat{c} \le0 $$

(12)

where

$$\begin{aligned} \hat{a} &= b(1 - t_{F}) - (t_{L} - t_{F})\\ \hat{b} &= - b(1 - t_{F})c_{F} - b(1 - t_{F})Kc_{L} - \bigl(c_{L}(1 - t_{L}) - (1 - t_{F})c_{F} \bigr)\\ \hat{c} & = bKc_{L}(1 - t_{F})c_{F} \end{aligned}$$

Under the situation c _L <c _F and t _L >t _F , we have $\hat {a} > 0$, $\hat{b} < 0$ and $\hat{c} < 0$, so there is a feasible range for T. More important, Q makes equality. When Kc _L >Q, the optimal transfer price is in the form

$$T^{*} = \frac{ - \hat{b} + \sqrt{\hat{b}^{2} - 4\hat{a}\hat{c}}}{2\hat{a}} $$

We refer π _A and π _B to the total profits derived from Path A and B, respectively. Hence,

$$\pi_{A} = \pi \biggl(\lambda_{A}^{*},T_{A}^{*} \bigl(\lambda_{A}^{*}\bigr) = \frac{\lambda_{A}^{*}bc_{F}(1 - t_{F}) - (1 - \lambda_{A}^{*})c_{L}(t_{F} - t_{L})}{\lambda _{A}^{*} [ b(1 - t_{F}) - (t_{L} - t_{F}) ]}\Big| \lambda_{A}^{*} = \frac{ - \tilde{b} + \sqrt{\tilde{b}^{2} - 4\tilde{a}\tilde{c}}}{2\tilde{a}}\biggr) $$

while

$$\begin{aligned} \pi_{B} = \pi\biggl(\lambda_{B}^{*} \bigl(T_{B}^{*}\bigr) & = \frac{c_{L} [ (1 - t_{F})(T_{B}^{*} - c_{F}) - (1 - t_{L})(T_{B}^{*} - c_{L}) ]}{(T - c_{L}) [ (b - 1)(1 - t_{F})(T_{B}^{*} - c_{F}) + (1 - t_{L})(T_{B}^{*} - c_{L}) ]},T_{B}^{*}\Big|T_{B}^{*}\\ &= \frac{ - \hat{b} + \sqrt{\hat{b}^{2} - 4\hat{a}\hat{c}}}{2\hat{a}}\biggr) \end{aligned}$$

In fact, we can prove $\lambda_{B}^{*}(T_{A}^{*}(\lambda_{A}^{*})) < \lambda_{A}^{*}$, but the solution ($\lambda_{B}^{*}(T_{A}^{*}(\lambda_{A}^{*})),T_{A}^{*}(\lambda_{A}^{*})$) is not feasible due to an invalid P<T, though bringing a higher profit. Therefore, the comparison π _A and π _B simply makes decision on the optimal solution for the headquarters. □

Proof of Theorem 5

Given fixed P,z, and T, consider the first partial derivatives of π _L taken with respect to λ:

$$\frac{\partial\pi_{L}}{\partial\lambda} = y(P)z(c_{L} - T) $$

• (1) If c _L <c _F , it is easy to see c _L −T<c _F −T≤0, thus $\frac{\partial\pi_{L}}{\partial\lambda} < 0$. The optimal $\lambda_{dc}^{*}$ for the retailer is $\lambda_{dc}^{*} = 0$, i.e., no offshoring.

• (2) If c _L >c _F , then $\lambda_{dc}^{*} = 0$ given T>c _L , $\lambda_{dc}^{*} = 1$ given c _F ≤T<c _L , and ∀λ∈[0,1] is optimal given T=c _L . Note that the retailer and headquarters play a Stackelberg game, where the headquarters act as the leader. Given the retailer’s response function, we analysis the decision of the headquarters.

  Consider the first partial derivatives of π taken with respect to T:

  $$\frac{\partial\pi(P,T,z,\lambda(P,T,z))}{\partial T} = y(P)z\lambda (t_{L} - t_{F}) $$

  It is easy to find that if t _L <t _F , then $T_{dc}^{*} = c_{F}$, and $\lambda_{dc}^{*} = 1$;

• (2a) if t _L >t _F , we discover that the local company makes decision on λ depending on the difference between c _L and the transfer price to be set by the headquarters. Therefore, when c _L >min{T _U ,T _L+}, $\lambda_{dc}^{*} = 1$, and all other optimal solutions are same as Theorem 1(a). Otherwise, offshoring occurs.

• (2b) if t _L <t _F , the optimal solutions are same as in Theorem 1(b).

 □

Proof of Theorem 6

Proof is similar to Theorem 5 except that Proposition 1 should be considered here. □