The implication of time-based payment contract in the decentralized assembly system

Abstract

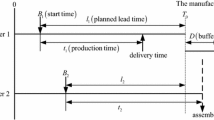
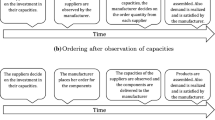
This paper investigates the impact of two time-based payment contracts in an assembly system that consists of one assembler and two suppliers, in which both suppliers’ production times are stochastic. The assembler initially chooses the contract type (delay payment contract vs on-time payment contract) and the buffer time, and two suppliers have to simultaneously determine their production lead times. We find that in equilibrium, both suppliers cut down their production lead times under the delay payment contract, and this makes them worse off than that under the on-time payment contract. Differently, the delay payment contract is the assembler’s dominant option. This is because by setting the buffer time, the assembler can significantly mitigate the possible delay risk caused by the suppliers’ decentralization under the delay payment contract. It also shows that the entire supply chain achieves the same service level under either the centralized condition or the decentralized condition, regardless of the applied payment contract type. Note that these results are robustness when we extend the model into the system containing N (N $>$ 2) independent suppliers.

Appendix

Proof of Lemma 1

Expending Eq. (4), we have:

$$\begin{aligned} C_{s_{i}}^{n}&= {h_{i}}\left\{ \int \limits _{0}^{{l_{i}}}{\int \limits _{0}^{{l_{j}}} {({l_{i}}-{t_{i}})}}{f_{i}}({t_{i}}){f_{j}}({t_{j}})d{t_{i}}d{t_{j}}\right. \nonumber \\&\left. +\int \limits _{{l_{j}}}^{\infty }{\int \limits _{0}^{{t_{j}}-{l_{j}}+{l_{i}}}{[( {t_{j}}-{l_{j}})-({t_{i}}-{l_{i}})}}]{f_{i}}({t_{i}}){f_{j}}({t_{j}})d{t_{i}} d{t_{j}}\right\} \nonumber \\&+{\beta _{i}}\int \limits _{{l_{i}}}^{\infty }{({t_{i}}-{l_{i}})}{f_{i}}({ t_{i}})d{t_{i}.} \end{aligned}$$

(17)

Take both the first-order conditions of (17), we can show that:

$$\begin{aligned} \frac{{\partial }C_{s_{i}}^{n}}{{\partial {l_{i}}}}&= {\beta _{i}}F({l_{i}} )+{h_{i}}{F_{i}}({l_{i}}){F_{j}}({l_{j}})+{h_{i}}\int \limits _{{l_{j}} }^{\infty }{\int \limits _{0}^{{l_{i}}+{t_{j}}-{l_{j}}}{{f_{i}}({t_{i}}){f_{j}} ({t_{j}})d{t_{i}}d{t_{j}}-{\beta _{i}}}}; \\ \frac{{{\partial ^{2}}}C_{s_{i}}^{n}}{{\partial {l_{i}}^{2}}}&= {h_{i}}{ f_{i}}({l_{i}}){F_{j}}({l_{j}})+{h_{i}}\int \limits _{{l_{j}}}^{\infty }{{f_{i} }({t_{j}}-{l_{j}}+{l_{i}})}{f_{j}}({t_{j}})d{t_{j}}+{\beta _{i}}{f_{i}}({ l_{i}})>0. \end{aligned}$$

Therefore, supplier’s expected cost is convex in $l_{i}$, and the optimal $l_{i}$ meets the first-order condition. We then demonstrate the uniqueness of the above results.

Considering the reaction curves of both suppliers in $\frac{{\partial } C_{s_{i}}^{N}}{{\partial {l_{i}}}}$, we assume that:

$$\begin{aligned} {G_{1}}({l_{1}},{l_{2}})=\frac{{\partial }C_{s_{1}}^{n}}{{\partial {l_{1}}}}= {\beta _{1}}F({l_{1}})+{h_{1}}{F_{1}}({l_{1}}){F_{2}}({l_{2}})+{h_{1}} \int \limits _{{l_{2}}}^{\infty }{\int \limits _{0}^{{l_{1}}+{t_{2}}-{l_{2}}}{{ f_{1}}({t_{1}}){f_{2}}({t_{2}})d{t_{1}}d{t_{2}}-{\beta _{1}}}}, \end{aligned}$$

and

$$\begin{aligned} {G_{2}}({l_{1}},{l_{2}})&= \frac{{\partial }C_{s2}^{n}}{{\partial {l_{2}}}}={ \beta _{2}}F({l_{2}})+{h_{2}}{F_{1}}({l_{1}}){F_{2}}({l_{2}})\nonumber \\&+{h_{2}} \int \limits _{{l_{1}}}^{\infty }{\int \limits _{0}^{{l_{2}}+{t_{1}}-{l_{1}}}{{ f_{1}}({t_{1}}){f_{2}}({t_{2}})d{t_{1}}d{t_{2}}-{\beta _{2}}}}. \end{aligned}$$

Subsequently, we can show that

$$\begin{aligned} \frac{{\partial G{_{1}}({l_{1}},{l_{2}})}}{{\partial {l_{1}}}}-\frac{{ \partial }G{{_{2}}({l_{1}},{l_{2}})}}{{\partial {l_{1}}}}&= {h_{1}}\int \limits _{{l_{2}}}^{\infty }{{f_{1}}({t_{2}}-{l_{2}}+{l_{1}})}{ f_{2}}({t_{2}})d{t_{2}}+{\beta _{1}}{f_{1}}({l_{1}})\nonumber \\&+{h_{2}}\int \limits _{{ l_{1}}}^{\infty }{{f_{2}}({l_{2}}+{t_{1}}-{l_{1}}){f_{1}}({t_{1}})d{t_{1}}>0}. \end{aligned}$$

Since $\frac{{\partial G{_{1}}({l_{1}},{l_{2}})}}{{\partial {l_{1}}}}-\frac{{ \partial G{_{2}}({l_{1}},{l_{2}})}}{{\partial {l_{1}}}}>0$, the response functions will meet once at most (Gurnani and Gerchak 2007). Also, referring to Friedman’s research (Friedman 1986, Theorem 2.4), there is always a Nash Equilibrium existing for a convex-payoff-functions game like ours. Therefore, the NE of both suppliers’ production lead times is unique. $\square$

Proof of Lemma 2

The assembler’s cost under delay payment contract, as shown in (9), can be represented as: ${C_{m}}=\beta A+\sum h_{i} {{B_{i}}}-C,(i=1,2),$ in which:

$$ \begin{aligned} A&= \int \limits _{{l_{1}}+D}^{\infty }{\int \limits _{0}^{{t_{1}}-{l_{1}}+{ l_{2}}}{({t_{1}}-{l_{1}}-D)}}{f_{1}}({t_{1}}){f_{2}}({t_{2}})d{t_{2}}d{t_{1}}\nonumber \\&+\int \limits _{{l_{2}}+D}^{\infty }{\int \limits _{0}^{{t_{2}}-{l_{2}}+{l_{1}}}{ ({t_{2}}-{l_{2}}-D)}}{f_{1}}({t_{1}}){f_{2}}({t_{2}})d{t_{1}}d{t_{2},} \\ B&= \int \limits _{{l_{1}}}^{{l_{1}}+D}{\int \limits _{0}^{{t_{1}}-{l_{1}}+{ l_{2}}}{(D-({t_{1}}-{l_{1}}))}}{f_{1}}({t_{1}}){f_{2}}({t_{2}})d{t_{2}}d{ t_{1}} \\&+ \int \limits _{{L_{2}}}^{{l_{2}}+D}{\int \limits _{0}^{{t_{2}}-{l_{2}}+{l_{1}}} {(D-({t_{2}}-{l_{2}}))}}{f_{1}}({t_{1}}){f_{2}}({t_{2}})d{t_{1}}d{t_{2}} +\int \limits _{0}^{{l_{1}}}{\int \limits _{0}^{{l_{2}}}D}{f_{1}}({t_{1}}){f_{2}} ({t_{2}})d{t_{1}}d{t_{2},} \\ C&= {\beta _{1}}\int \limits _{{l_{1}}}^{\infty }{({t_{1}}-{l_{1}}){f_{1}}({ t_{1}})}d{t_{1}}+{\beta _{2}}\int \limits _{{l_{2}}}^{\infty }{({t_{2}}-{l_{2}} ){f_{2}}({t_{2}})}d{t_{2}}\ \ \ i,j=1,2\, \& \,i\ne j. \end{aligned}$$

Subsequently, obtaining the first-order condition of $D$ gives rise to the equilibrium result. $\square$

Proof of Proposition 2

We first assume that compared to the on-time payment contract, $\Delta {l_{1}}$ and $\Delta {l_{2}}$ are the reduced periods of suppliers’ production lead times under the delay payment contract, $\Delta {l_{i}}=l_{_{i}}^{o}-l_{_{i}}^{n}$. Similarly, we assume that the assembler’s buffer time also increases $\Delta D$ under the delay payment contract, $\Delta D=D^{n}-D^{o}.$ Intuitively, it has $\Delta {l_{1}} <\Delta D<\Delta {l_{2}}$ ($\Delta {l_{1}}<\Delta {l_{2}}$). Therefore, we can rewrite the assembler’s cost function under the on-time payment, where:

$$\begin{aligned} C_{m}^{o}&= \beta E({{t_{2}}-{l_{2}}-D^{o}+{({t_{1}}-{l_{1}}-{t_{2}}+{l_{2}} )^{+})}^{+}}\nonumber \\&+\,{h_{1}}E({D^{o}-\max ({t_{1}}-{l_{1}},0)+{({t_{2}}-{l_{2}} -D^{o})^{+})}^{+}} \nonumber \\&+\,{h_{2}}E({D^{o}-\max ({t_{2}}-{l_{2}},0)+{({t_{1}}-{l_{1}}-D^{o})^{+})} ^{+}}-\sum \limits _{i=1}^{2}{{\beta _{i}}E{{({t_{i}}-{l_{i}})}^{+}.}} \end{aligned}$$

(18)

If the assembler just chooses a buffer time ${D^{n}}={D^{o}}+\Delta {l_{2}}$ under the delay payment contract, its cost:

$$\begin{aligned} C_{m}^{n}&= \beta E({{t_{2}}-{l_{2}}-D^{o}+{({t_{1}}-{l_{1}}-{t_{2}}+{l_{2}} -\Delta {l_{2}})^{+})}^{+}} \nonumber \\&+\,{h_{1}}E({D^{o}+\Delta {l_{2}}-\max ({t_{1}}-{l_{1}}+\Delta {l_{1}},0)-{({t_{2}}-{l_{2}}-{t_{1}}+{l_{1}}+\Delta {l_{2}})^{+})}^{+}} \nonumber \\&+\,{h_{2}}E({D^{o}-\max ({t_{2}}-{l_{2}},0)-{({t_{1}}-{l_{1}}-{t_{2}}+{l_{2}}-\Delta {l_{2}})^{+})}^{+}}\nonumber \\&-\,\sum \limits _{i=1}^{2}{{\beta _{i}}{{({t_{i}}-{l_{i}}+\Delta {l_{i}})}^{+}.}} \end{aligned}$$

(19)

From Eqs. (18) and (19), we can easily find that assembler’s penalty cost, inventory holding cost for component 2 are smaller and the compensation is larger under delay payment than the on-time payment, while the only inventory holding cost is not easy to confirm. Note that only in the extreme cases when the gap $\Delta$ between $\Delta {l_{1}}$ and $\Delta {l_{2}}$ is very large, then the assembler may be better off under the on-time payment contract. However, this circumstance occurs only if the both suppliers’ production times follow the discrete distribution. Otherwise, if both times follow the continuous distribution, it is impossible for one factor changes slightly but the others react dramatically. Therefore, in general we can conclude that it is always profitable for the assembler to choose the delay payment contract with the application of buffer time.$\square$

Proof of Lemma 3

The centralized system’s cost can be extended to:

$$\begin{aligned} {C_{C}}&= {h_{1}}\left[ \int \limits _{{L_{2}}}^{\infty }{\int \limits _{0}^{{t_{2}}-{ L_{2}}+{L_{1}}}{[({t_{2}}-{L_{2}})-(}}{t_{1}}-{L_{1}})]{f_{1}}({t_{1}}){f_{2} }({t_{2}})d{t_{2}}d{t_{1}}\right. \nonumber \\&\left. +\int \limits _{0}^{{L_{2}}}{\int \limits _{0}^{{L_{1}} }{({L_{1}}-}}{t_{1}}){f_{1}}({t_{1}}){f_{2}}({t_{2}})d{t_{2}}d{t_{1}}\right] \nonumber \\&+{h_{2}}\left[ \int \limits _{{L_{1}}}^{\infty }{\int \limits _{0}^{{t_{1}}-{L_{1}}+{ L_{2}}}{[({t_{1}}-{L_{1}})-(}}{t_{2}}-{L_{2}})]{f_{1}}({t_{1}}){f_{2}}({t_{2} })d{t_{2}}d{t_{1}}\right. \nonumber \\&\left. +\int \limits _{0}^{{L_{2}}}{\int \limits _{0}^{{L_{1}}}{({ L_{2}}-}}{t_{2}}){f_{1}}({t_{1}}){f_{2}}({t_{2}})d{t_{2}}d{t_{1}}\right] \nonumber \\&+\beta \left[ [\int \limits _{{L_{1}}}^{\infty }{\int \limits _{0}^{{t_{1}}-{ L_{1}}+{L_{2}}}{({t_{1}}-{L_{1}})}}{f_{1}}({t_{1}}){f_{2}}({t_{2}})d{t_{2}}d{ t_{1}}\right. \nonumber \\&\left. +\int \limits _{{L_{2}}}^{\infty }{\int \limits _{0}^{{t_{2}}-{L_{2}}+{ L_{1}}}{({t_{2}}-{L_{2}})}}{f_{1}}({t_{1}}){f_{2}}({t_{2}})d{t_{2}}d{t_{1}}\right] . \end{aligned}$$

(20)

Taking the first-order derivatives of (${L_{1}},{L_{1}}$), we gain:

$$\begin{aligned} \frac{{\partial {C_{c}}}}{{\partial {L_{1}}}}&= h{_{1}}\left[ {F_{1}}({L_{1}}){ F_{2}}({L_{2}})\right. \nonumber \\&\left. +\int \limits _{{L_{2}}}^{\infty }{\int \limits _{0}^{{t_{2}} -{\mathrm {L}_{2}}+{L_{1}}}{{f_{1}}({t_{1}}){f_{2}}({ t_{2}})d{t_{1}}d{t_{2}}}}\right] -({h_{2}}+\beta )\int \limits _{{L_{1}}}^{\infty }{ \int \limits _{0}^{{\mathrm {t}_{1}}\mathrm {-}{\mathrm {L}_{1}}+{ \mathrm {L}_{2}}}{{f_{1}}({t_{1}}){f_{2}}({t_{2}})d{t_{1}}d{t_{2}}}} . \nonumber \\ \frac{{\partial {C_{c}}}}{{\partial {L_{2}}}}&= h{_{2}}\left[ {F_{1}}({L_{1}}){ F_{2}}({L_{2}})\right. \nonumber \\&\left. +\int \limits _{{L_{1}}}^{\infty }{\int \limits _{0}^{{t_{1}} -{\mathrm {L}_{1}}+{L_{2}}}{{f_{1}}({t_{1}}){f_{2}}({t_{2}})d{t_{1}}d {t_{2}}}}\right] -({h_{1}}+\beta )\int \limits _{{L_{2}}}^{\infty }{\int \limits _{0}^{{ \mathrm {t}_{2}}-{\mathrm {L}_{2}}+{\mathrm {L}_{1}}}{{f_{1}}( {t_{1}}){f_{2}}({t_{2}})d{t_{1}}d{t_{2}}}} . \nonumber \end{aligned}$$

Investigating the Hessian Matrix of $({L_{1}},{L_{2}})$:

$$\begin{aligned} \frac{{{\partial ^{2}}{C_{c}}}}{{\partial {L_{1}}^{2}}}&= {\mathrm {h}_{1}}\left[ { f_{1}}({L_{1}}){F_{2}}({L_{2}})+\int \limits _{{L_{2}}}^{\infty }{{f_{1}}({ t_{2}}-{L_{2}}+{L_{1}}){f_{2}}({t_{2}})d{t_{2}}}\right] \nonumber \\&+({h_{2}}+\beta )[\int \limits _{0}^{{L_{2}}}{f_{1}}({L_{1}}){f_{2}}({t_{2}})d{t_{2}} \nonumber \\&+\int \limits _{{L_{1}}}^{\infty }{{f_{2}}({t_{1}}-{L_{1}}+{L_{2}}){f_{1}}({ t_{1}})d{t_{1}}}]=({h_{1}}+{h_{2}}+\beta )[{f_{1}}({L_{1}}){F_{2}}({L_{2}} )+A]>0, \end{aligned}$$

$$\begin{aligned} \frac{{{\partial ^{2}}{C_{c}}}}{{\partial {L_{2}}^{2}}}=({h_{1}}+{h_{2}} +\beta )({F_{1}}({L_{1}}){f_{2}}({L_{2}})+A)>0, \end{aligned}$$

$$\begin{aligned} \frac{{{\partial ^{2}}{C_{c}}}}{{\partial {L_{1}}\partial {L_{2}}}}=\frac{{{ \partial ^{2}}{C_{c}}}}{{\partial {L_{2}}\partial {L_{1}}}}=A({h_{1}}+{h_{2}} +\beta ). \end{aligned}$$

Since that $\frac{{{\partial ^{2}}{C_{c}}}}{{\partial {L_{1}}^{2}}}\frac{{{ \partial ^{2}}{C_{c}}}}{{\partial {L_{2}}^{2}}}-\frac{{{\partial ^{2}}{C_{c}} }}{{\partial {L_{1}}\partial {L_{2}}}}\frac{{{\partial ^{2}}{C_{c}}}}{{ \partial {L_{2}}\partial {L_{1}}}}>0$, the system’s total cost is joint convex in $({L_{1}},{L_{2}})$. $\square$