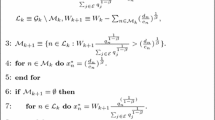Multiple agents finitely repeated inspection game with dismissals

Abstract

This paper deals with an inspection game between a single inspector and several independent (potential) violators over a finite-time horizon. In each period, the inspector gets a renewable inspection resource, which cannot be saved and used in future periods. The inspector allocates it to inspect the (potential) violators. Each violator decides in each period whether to violate or not, and in what probability. A violation may be detected by the inspector with a known and positive probability. When a violation is detected, the responsible violator is “dismissed” from the game. The game terminates when all the violators are detected or when there are no more remaining periods. An efficient method to compute a Nash equilibrium for this game is developed, for any possible value of the (nominal) detection probability. The solution of the game shows that the violators always maintain their detection probability below 0.5.

Appendix

Proof of Lemma 1:

If $W\ge \sum _{j\in {\mathcal {N}}(t)} \alpha _j$, Scenario (i) is relevant, and the empty set of conditions of Scenario (i) is satisfied.

Otherwise, Scenario (ii) is relevant. Suppose that ${\mathcal {N}}(t)=\{i_1,\ldots ,i_k\}$, so $m=i_k(=i_{n(t)})$ and is fixed (following, we will also prove this for ${\mathcal {N}}(t)=\{i_1,\ldots ,i_k,\ldots , i_{n(t)}\}$).

If $\beta \le \frac{1}{2}$, the single condition of Case (A) is satisfied. Otherwise, $\beta > \frac{1}{2}$, i.e., Condition 1 of Case (B) and of Case (C) is satisfied. We will show that there is a $u\in \{i_{k-1},i_{k-2},\ldots ,i_1,0\}$, such that also conditions 2–5 of Case (B) or conditions 2–5 of Case (C) are satisfied.

Consider Case (B):

We will show that there is always a $u\in \{i_{k-1},i_{k-2},\ldots ,i_1,0\}$, such that Condition 2 and Condition 3 of Case (B) are satisfied. According to (14)–(16),

$$\begin{aligned} \infty \equiv A_0>A_{i_1}>\cdots > A_{i_k}(=A_{i_{n(t)}})>A_{i_{k+1}}\equiv 0. \end{aligned}$$

If for all $v\in \{i_{k-1},\ldots ,i_1,0\}$, $A_v>2\beta A_{i_k}$, then $u=i_{k-1}$ satisfies the conditions, as $A_{u+1}=A_{i_k}<2\beta A_{i_k}$ because $\beta > \frac{1}{2}$. Otherwise, if for all $v\in \{i_{k-1}, i_{k-2},\ldots ,i_1\}$, $A_v<2\beta A_{i_k}$, then $u=0$ satisfies the conditions, as $\infty \equiv A_{0}>2\beta A_{i_k}$. Otherwise, there must be a $u\in \{i_{k-1},\ldots ,i_1,0\}$ such that Conditions 2 and Condition 3 of Case (B) are satisfied. Now, using this $u$, if also Condition 4 is satisfied, then we are done.¹

Otherwise, if for the specific $u$ Condition 4 of Case (B) is not satisfied; Consider Case (C) with the same $u$. Clearly, Condition 4 of Case (C) is satisfied as it is the negation of Condition 4 of Case (B). Also, using the existence of Condition 4 of (C) and Condition 2 of (B); Condition 2 of (C) is satisfied, as $W >\sum _{j=i_1}^{u} \alpha _j+\frac{\sum _{j=u+1}^{i_k} \alpha _j A_j }{2 \beta A_{i_k}}\ge \sum _{j=i_1}^{u} \alpha _j+\frac{\sum _{j=u+1}^{i_k} \alpha _j A_j }{A_{u}}$. If also Condition 3 is satisfied, then all the conditions of Case (C) are satisfied with this $u$,² and the proof is completed.

Otherwise, increase $u$ into $u'\leftarrow u+1$, and consider Case (C) with $u'$. Condition 2 of Case (C) with $u'$ is satisfied as it is the negation of Condition 3 of Case (C) with $u$. Condition 4 of Case (C) with $u'$ is satisfied using the existence of Condition 2 of Case (C) with $u'$ and Condition 3 of Case (B) with $u$. So, if also Condition 3 of Case (C) is satisfied, then all the conditions of Case (C) are satisfied with this $u'$, and the proof is completed, Case (C) holds for this $u'$.

Otherwise, consider Case (C) with $u''\leftarrow u'+1$. Again, condition 2,4, (and 5) will be satisfied from the same reasons as before, and the only possible obstacle can be Condition 3. This process can be repeated until the point where Case (C) is considered with $i_{k-1}$. Under this substitution, Condition 3 of (C) is always satisfied, as it becomes $W \le \sum _{j=i_1}^{i_{k}} \alpha _j$, which $W$ clearly satisfies. Hence, when $m=i_k(=i_{n(t)})$ and $\beta > \frac{1}{2}$, there is a a $u\in \{i_{k-1},i_{k-2},\ldots ,i_1,0\}$ such that all the conditions of Case (B) or of Case (C) are satisfied.

Now, suppose that ${\mathcal {N}}(t)=\{i_1,\ldots ,i_k,\ldots , i_{n(t)}\}$. That is, $m$ can be increased. If $\beta \le \frac{1}{2}$, the single condition of Case (A) is satisfied. Otherwise, $\beta > \frac{1}{2}$, i.e., Condition 1 of Case (B) and of Case (C) is satisfied. Consider Case (B) with $m=i_k$. We already showed that for $m=i_k$, there is always a $u\in \{i_{k-1},i_{k-2},\ldots ,i_1,0\}$, such that conditions 2–3 of Case (B) are satisfied. Also, Condition 5 of (B) is always satisfied when $m=i_k$ (see footnote 3). So, if also Condition 4 of (B) is satisfied, then we are done. Else, consider Case (C) with the same $u$ and with $m=i_k$. As we showed above, conditions 4 and 2 are immediate. So, if also conditions 3 and 5 of Case (C) are satisfied, then the proof is completed; all the conditions of Case (C) with this $u$ and with $m=i_{k}$ are satisfied. Else, there are three options:

• 1. Condition 3 is satisfied, Condition 5 is not.

• 2. Condition 5 is satisfied, Condition 3 is not.

• 3. Both conditions are not satisfied.

$(1)$ Condition 3 is satisfied, Condition 5 is not:

In this option, the existence of Condition 3 of Case (C), i.e., $W \le \sum _{j=i_1}^{u} \alpha _j+\frac{\sum _{j=u+1}^{i_k} \alpha _j A_j }{A_{u+1}}$, and the negation of Condition 5 of Case (C), i.e., $W >\sum _{j=i_1}^{u} \alpha _j+\frac{\sum _{j=u+1}^{i_k} \alpha _j A_j }{2 \beta A_{i_{k+1}}}$, imply that $A_{u+1}<2 \beta A_{i_{k+1}}$.

As with this $u$ and with $m=i_k$ Condition 2 of Case (B) is satisfied, that is, $A_u \ge 2 \beta A_{i_{k}}$, and as $2 \beta A_{i_{k}}>2 \beta A_{i_{k+1}}$ by (14), conditions 2 and 3 of Case (B) are satisfied with this $u$ and with $m=i_{k+1}$.

Hence, consider Case (B) with this $u$ and with $m=i_{k+1}$. Condition 5 of Case (B) is satisfied as it exactly the negation of Condition 5 of Case (C) with this $u$ and with $m=i_k$. If also Condition 4 of Case (B) is satisfied, then the proof is completed; all the conditions of Case (B) with this $u$ and with $m=i_{k+1}$ are satisfied.

Otherwise, consider Case (C) with this $u$ and with $m=i_{k+1}$. Again, conditions 4 and 2 are immediate. Conditions 3 is also immediate as Condition 3 of Case (C) with the same $u$ and with $m=i_{k}$ is satisfied, and now the right term of Condition 3 is only increased. So, if also Condition 5 of Case (C) is satisfied, then the proof is completed; all the conditions of Case (C) with this $u$ and with $m=i_{k+1}$ are satisfied.

Otherwise, again, from the existence of Condition 3 of Case (C) and the non-existence of Condition 5 of Case (C), we can deduce that conditions 2 and 3 of Case (B) are satisfied with the same $u$ and with $m=i_{k+2}$, and we consider Case (B) with this $u$ and with $m=i_{k+2}$. Continuing in this process, eventually, all the conditions of Case (B) will be satisfied, as the right term of Condition 4 of Case (B) increases with the increment of $m$, or all the conditions of (C) will be satisfied, as the right term of Condition 5 of Case (C) increases with the increment of $m$, and when $m=i_{n(t)}$, Condition 5 of (C) is always satisfied (see footnote 4).

$(2)$ Condition 5 is satisfied, Condition 3 is not:

In this option, from the restriction on $W$, i.e., $W\le \sum _{j=i_1}^{i_k} \alpha _j$, and from the existence of Condition 5 of Case (C), we cannot know for sure whether

• (I) $\frac{\sum _{j=u+1}^{i_k} \alpha _j A_j}{2 \beta A_{i_{k+1}}}< \sum _{j=u+1}^{i_k} \alpha _j$, or

• (II) $\sum _{j=u+1}^{i_k} \alpha _j <\frac{\sum _{j=u+1}^{i_k} \alpha _j A_j}{2 \beta A_{i_{k+1}}}$ (the equal sign fits both options, of course).

Suppose that (I) is the right one:

So, as $\frac{\sum _{j=u+1}^{i_k} \alpha _j A_j}{2 \beta A_{i_{k+1}}}< \sum _{j=u+1}^{i_k} \alpha _j$, there must be indexes $j \in \{u+1,\ldots ,i_{k}\}$ such that $A_j \le 2 \beta A_{i_{k+1}}$. Further, from the existence of Condition 5 of Case (C) with $u$ and with $m=i_k$ and the negation of Condition 3 of Case (C), $A_{u+1}> 2 \beta A_{i_{k+1}}$, so index $u+1$ is not one of them. Hence, let $v \in \{u+1,\ldots ,i_{k-1}\}$ be the smallest index such that $A_v\ge 2 \beta A_{i_{k+1}}\ge A_{v+1}$ (note that $v\ge u+1$), and consider Case (B) with $v$ and with $m=i_{k+1}$. Conditions 2–3 are (of course) satisfied. Condition 4 of Case (B) is: $W \le ^? \sum _{j=i_1}^{v} \alpha _j+\frac{\sum _{j=v+1}^{i_{k+1}} \alpha _j A_j }{2 \beta A_{i_{k+1}}}$. Condition 5 of Case (B) is: $W \ge ^? \sum _{j=i_1}^{v} \alpha _j+\frac{\sum _{j=v+1}^{i_{k}} \alpha _j A_j }{2 \beta A_{i_{k+1}}}$. If conditions 4 and 5 are satisfied, then the proof is completed; all the conditions of Case (B) with this $v$ and with $m=i_{k+1}$ are satisfied. Otherwise, note that if Condition 5 is not satisfied, then Condition 4 is satisfied, so there are two options:

• (A2) Condition 5 is not satisfied, Condition 4 is satisfied.

• (B2) Condition 4 is not satisfied, Condition 5 is satisfied.

(A2) Condition 5 is not satisfied, Condition 4 is satisfied:

So, $W\le \sum _{j=i_1}^{v} \alpha _j+\frac{\sum _{j=v+1}^{i_{k-1}} \alpha _j A_j }{2 \beta A_{i_{k+1}}}$.

Consider Case (C) with $\bar{u}\leftarrow u+1$ and with $m=i_{k}$. Condition 2 is satisfied as it exactly the negation of Condition 3 of Case (C) with $u$ and with $m=i_{k}$. Condition 4 is satisfied using Condition 2 of Case (C) with $\bar{u}$ and with $m=i_{k}$, and Condition 3 of Case (B) with $u$ and with $m=i_{k}$. Condition 5 is satisfied using the existence Condition 5 of Case (B) with $v$ and with $m=i_{k+1}$, because $u+1\le v$ and Condition 5 of (C): $W \le ^?\sum _{j=i_1}^{u+1} \alpha _j+\frac{\sum _{j=u+2}^{i_k} \alpha _j A_j }{2 \beta A_{i_{k+1}}}$. As $W\le \sum _{j=i_1}^{v} \alpha _j+\frac{\sum _{j=v+1}^{i_{k}} \alpha _j A_j }{2 \beta A_{i_{k+1}}}$, suppose negatively that Condition 5 of Case (C) with $\bar{u}$ and with $m=i_{k}$ is not satisfied, that is, $W >\sum _{j=i_1}^{u+1} \alpha _j+\frac{\sum _{j=u+2}^{i_k} \alpha _j A_j }{2 \beta A_{i_{k+1}}}$, implying that: $\sum _{j=i_1}^{u+1} \alpha _j+\frac{\sum _{j=u+2}^{i_k} \alpha _j A_j }{2 \beta A_{i_{k+1}}}< \sum _{j=i_1}^{v} \alpha _j+\frac{\sum _{j=v+1}^{i_{k}} \alpha _j A_j }{2 \beta A_{i_{k+1}}}$, a contradiction. So, if also Condition 3 of Case (C) is satisfied, then the proof is completed; all the conditions of Case (C) with $\bar{u}$ and with $m=i_{k}$ are satisfied.

Otherwise, consider Case (C) with $m=i_{k}$, and with $\tilde{u}\leftarrow \bar{u}+1(=u+2)$. Continuing in this process, eventually, Case (C) will hold for some $u^*$, as Condition 3 of Case (C) is always satisfied for $u^*=i_{k-1}$ and $m=i_{k}$.

(B2) Condition 4 is not satisfied, Condition 5 is satisfied:

So, $W>\sum _{j=i_1}^{v} \alpha _j+\frac{\sum _{j=v+1}^{i_{k+1}} \alpha _j A_j }{2 \beta A_{i_{k+1}}}$.

Consider Case (C) with $\bar{u}\leftarrow u+1$ and with $m=i_{k}$. Condition 2 is satisfied as it exactly the negation of Condition 3 of Case (C) with $u$ and $m=i_{k}$. Condition 4 is satisfied using Condition 2 of (C) with $\bar{u}$ and with $m=i_{k}$, and Condition 3 of Case (B) with $u$ and $m=i_{k}$. Condition 5 is satisfied using the existence of Condition 5 of Case (B) with $v$ and $m=i_{k+1}$, because $u+1\le v$ and Condition 5 of (C): $W \le ^?\sum _{j=i_1}^{u+1} \alpha _j+\frac{\sum _{j=u+2}^{i_k} \alpha _j A_j }{2 \beta A_{i_{k+1}}}$, and $\sum _{j=i_1}^{u+1} \alpha _j+\frac{\sum _{j=u+2}^{i_k} \alpha _j A_j }{2 \beta A_{i_{k+1}}}> \sum _{j=i_1}^{v} \alpha _j+\frac{\sum _{j=v+1}^{i_{k}} \alpha _j A_j }{2 \beta A_{i_{k+1}}}$. So, if also Condition 3 of (C) is satisfied, then the proof is completed; all the conditions of Case (C) with $\bar{u}$ and with $m=i_{k}$ are satisfied.

Otherwise, consider Case (C) with $m=i_{k}$ and with $\tilde{u}=\bar{u}+1=u+2$. Continuing in this process, eventually, Case (C) will hold for some $u^*$, as Condition 3 of (C) is always satisfied for $u^{*}=i_{k-1}$ and $m=i_{k}$.

Suppose that (II) is the right one:

So, $\frac{A_j}{2 \beta A_{i_{k+1}}} >1$ for $j=u+1,\ldots ,i_k$ and there cannot be an index $u$ and $m=i_{k+1}$ such that conditions 2–3 of Case (B) are satisfied. Consider Case (C) with $u'\leftarrow u+1$ and with $m=i_k$. Condition 2 is satisfied as it is the negation of Condition 3 of Case (C) with $u$ and with $m=i_k$. Condition 4 is satisfied using the existence of Condition 3 of Case (B) and of Case (C) with $u$ and with $m=i_k$. Condition 5 is satisfied using the restriction on $W$ and the fact that $\frac{A_j}{2 \beta A_{i_{k+1}}} >1$ for $j=u+2,\ldots ,i_k$. So, if also Condition 3 is satisfied, then the proof is completed; all the conditions of Case (C) with $u'\leftarrow u+1$ and with $m=i_{k}$ are satisfied.

Otherwise, consider Case (C) with $u''\leftarrow u'+1(=u+2)$ and with $m=i_k$. Continuing in this process, eventually, all the conditions of Case (C) will be satisfied, as the right term of Condition 3 of (C) increases with the increment of $u$, and as for $u=i_{k-1}$, Condition 3 of (C) is always satisfied as it becomes: $W \le \sum _{j=i_1}^{i_{k}} \alpha _j$, which is the restriction on $W$.

$(3)$ Conditions 3 and 5 are not satisfied:

Consider Case (C) with $v\leftarrow u+1$ and with $m=i_k$. Then, Condition 2 of Case (C) is satisfied as it is the negation of Condition 3 of Case (C) with $u$ and with $m=i_k$. Condition 4 is satisfied using the existence of Condition 2 of Case (C) with $v=u+1$ and with $m=i_k$, and using Condition 3 of Case (B) with $u$ and with $m=i_k$. Hence, we are left with conditions 3 and 5 of Case (C). If also they are satisfied, then the proof is completed; all the conditions of Case (C) with $v$ and with $m=i_{k}$ are satisfied.

Otherwise, if Condition 3 is satisfied and Condition 5 is not, return to $(1)$ with $v$ and with $m=i_k$. Otherwise, if Condition 5 is satisfied and Condition 3 is not, return to $(2)$ with $v$ and with $m=i_k$. Otherwise, if both are not satisfied, then consider Case (C) with $v'\leftarrow v+1(=u+2)$ and with $m=i_k$. Continuing in this process, if for all $\hat{v}\in \{u+2,\ldots ,i_{k-2}\}$ both conditions are not satisfied, then for $\tilde{v}=i_{k-1}$, Condition 3 is satisfied. So, if also Condition 5 is satisfied, then the proof is completed; all the conditions of Case (C) with $\tilde{v}$ and with $m=i_{k}$ are satisfied. Otherwise, if Condition 5 of Case (C) is not satisfied for $\tilde{v}$ and with $m=i_k$, then together with the restriction on $W$, this implies that $A_{i_{k-1}}\le 2 \beta A_{i_{k+1}}$. So, there must be an index $V\in \{0,\ldots ,i_{k-1}\}$ such that conditions 2 and 3 of Case (B) with $m=i_{k+1}$ are satisfied. Further, Condition 5 of Case (B) with that $V$ and with $m=i_{k+1}$ is immediate using all the negations of Condition 5 of (C) with $\hat{v}\in \{u+1,\ldots ,i_{k-1}\}$ and with $m=i_k$. So, if also Condition 4 is satisfied, then the proof is completed; all the conditions of Case (B) with this $V$ and with $m=i_{k+1}$ are satisfied.

Otherwise, consider Case (C) with $V$, and with $m=i_{k+1}$. Again, conditions 2 and 4 are satisfied from the same reasons as before, and we are left with conditions 3 and 5 of Case (C). Continuing in this process, eventually, all the conditions of Case (B) or all the conditions of Case (C) will be satisfied, as the right terms of Condition 4 of (B) and of Conditions 3 and 5 of (C) increase in this process, and there is a restriction on $W$. Further, Condition 5 of (C) with $m=i_{n(t)}$ is always satisfied (see footnote 4). $\square$

Proof of Theorem 1:

(i) $\underline{W\ge \sum _{j\in {\mathcal {N}}(t)} \alpha _j}$:

Assume that $(x^*(t),y^*(t))$ satisfies (25). Then, clearly, $x^*(t) \in {\mathcal {X}}(t)$ and $y^*(t)\in {\mathcal {Y}}(t)$. Now, as $x_i(t)^*>0$ for each $i \in {\mathcal {N}}(t)$, each agent’s best response to $x_i^*(t)$ is given by (22), that is, $y_i(t)^{opt}=\min \{1,\frac{ \alpha _i}{2\beta \alpha _i}\}= \min \{1,\frac{1}{2\beta }\}$. In particular, $y^*(t)$ is a best response to $x^*(t)$.

On the other hand, given $y^*(t)$, $A_i y_i^*(t)=A_i$ or $A_i y_i^*(t)=\frac{A_i}{2\beta }$ for each $i \in {\mathcal {N}}(t)$. So, according to (14), the inspector’s best response to $y^*(t)$ is to allocate to each agent, by their $A_i$-order, the maximum amount possible. In particular, $x^*(t)$ is a best response to $y^*(t)$. As $y^*(t)$ is a best response to $x^*(t)$, and $x^*(t)$ is a best response to $y^*(t)$, $(x^*(t),y^*(t))$ is a Nash equilibrium.

(ii)$\underline{\sum _{j=i_1}^{i_{k-1}} \alpha _j \!<\! W \!\le \! \sum _{j=i_1}^{i_k}\alpha _j \ { for}\ k\!<\! n(t) \ { or}\ \sum _{j=i_1}^{i_{k-1}} \alpha _j \!<\! W \!<\! \sum _{j=i_1}^{i_k}\alpha _j \ { for}\ k\!=\! n(t)}$:

($A$):

Assume that $\beta < \frac{1}{2}$, and that $(x^*(t),y^*(t))$ satisfies (26). Then, clearly, $x^*(t) \in {\mathcal {X}}(t)$ and $y^*(t) \in {\mathcal {Y}}(t)$. Now, as $x_i^*(t)>0$ for $i \in \{i_1, \ldots , i_k\}$; for $i=i_1, \ldots , i_k$, each agent’s best response to $x_i^*(t)$ is given by (22). That is, $y_i(t)^{opt}=\min \{1,\frac{\alpha _i}{2\beta x_i(t)}\}= \min \{1,\frac{1}{2\beta }\}=1$ (as $\beta < \frac{1}{2}$) for $i=i_1,\ldots , i_{k-1}$, and $y_{i_k}(t)^{opt}=\min \{1,\frac{\alpha _{i_k}}{2\beta x_{i_k}(t)}\}= \min \{1,\frac{\alpha _{i_k}}{2\beta (W-\sum _{j=i_1}^{i_{k-1}} \alpha _j)}\}$ for $i=i_k$. Now, as $W \le \sum _{j=i_1}^{i_k}\alpha _j < \sum _{j=i_1}^{i_{k-1}}\alpha _j+\frac{\alpha _{i_k}}{2\beta }$, this implies that $\frac{\alpha _{i_k}}{2\beta (W-\sum _{j=i_1}^{i_{k-1}} \alpha _j)}>1$, so $y_{i_k}(t)^{opt}=1$. Further, as $x_i^*(t)=0$ for $i \in \{i_{k+1}, \ldots , i_{n(t)}\}$, for $i=i_{k+1}, \ldots , i_{n(t)}$, each agent’s best response to $x_i^*(t)$ is given by (24). That is, $y_i(t)^{opt}=1$. Hence, $y^*(t)$ is a best response to $x^*(t)$.

On the other hand, given $y^*(t)$, $A_i y_i^*(t)=A_i$ for each $i \in {\mathcal {N}}(t)$. By (14), the inspector’s best response to $y^*(t)$ is to allocate to each agent, by their $A_i$-order, the maximum amount possible. In particular, $x^*(t)$ is a best response to $y^*(t)$. As $y^*(t)$ is a best response to $x^*(t)$, and $x^*(t)$ is a best response to $y^*(t)$, $(x^*(t),y^*(t))$ is a Nash equilibrium.

($B$):

Assume that there exists a $u \in \{i_{k-1}, \ldots , 0\}$ and an $m \in \{i_k, \ldots , i_{n(t)}\}$, such that conditions 1–5 of Case (B) are satisfied, and that $(x^*(t),y^*(t))$ satisfies (27).

We first show that $x^*(t)\in {\mathcal {X}}(t)$. For $i=u+1,\ldots , m-1$, $[x^*_i(t)=\frac{\alpha _i A_i}{2 \beta A_{m}}\le ^? \alpha _i]\Leftrightarrow [\frac{A_i}{2 \beta }\le ^? A_{m}]$. Now, according to (14) and to Condition 3 of Case (B), $\frac{A_{m-1}}{2 \beta }<\cdots <\frac{A_{u+1}}{2 \beta }\le A_{m}$, so this is satisfied.

Further, for $i=m$, $[x^*_{m}(t)=W-\sum _{j=i_1}^{m-1} x^*_j(t)\le \alpha _{m}]\Leftrightarrow [W\le \sum _{j=i_1}^{m-1}x^*_j(t)+\alpha _{m}]\Leftrightarrow [W \le \sum _{j=i_1}^{u} \alpha _j+\frac{\sum _{j=u+1}^{m-1} \alpha _j A_j }{2 \beta A_{m}}+\alpha _{m}]$. Now, as $W \le \sum _{j=i_1}^{u} \alpha _j+\frac{\sum _{j=u+1}^{m} \alpha _j A_j }{2 \beta A_{m}}$ by Condition 4 and as $\frac{\sum _{j=u+1}^{m} \alpha _j A_j }{2 \beta A_{m}}<\frac{\sum _{j=u+1}^{m-1} \alpha _j A_j }{2 \beta A_{m}}+\alpha _{m}$ because $\frac{\alpha _{m}}{2 \beta }<\alpha _{m}$, this is satisfied.

Also, for $i=m$, $[x^*_{m}(t)=W-\sum _{j=i_1}^{m-1} x^*_j(t)\ge 0]\Leftrightarrow [W\ge \sum _{j=i_1}^{m-1}x^*_j(t)]\Leftrightarrow [W\ge \sum _{j=i_1}^{u} \alpha _j+\frac{\sum _{j=u+1}^{m-1} \alpha _j A_j }{2 \beta A_{m}}]$, which is Condition 5 and so it is satisfied. Finally, it is clear that $\sum _{j=i_1}^{m} x_j^*(t)=W$, so $x^*(t)\in {\mathcal {X}}(t)$.

We next show that $y^*(t)\in {\mathcal {Y}}(t)$. Clearly, as $\beta > \frac{1}{2}$, by Condition 1, $y_i^*(t)\le 1$ for $i=i_1,\ldots , u$. Further, by (14), $A_{u+1}>\cdots >A_{m}$, so $y_i^*(t)\le 1$ for $i=u+1,\ldots , m$. Finally, $y_i^*(t)=1$ for $i=m+1,\ldots ,i_{n(t)}$. So, $y^*(t)\in {\mathcal {Y}}(t)$.

Now, as $x_i^*(t)>0$ for $i \in \{i_1, \ldots , m-1\}$, each agent’s best response to $x_i^*(t)$ is given by (22) for $i =i_1, \ldots , m-1$. That is, $y_i(t)^{opt}=\min \{1,\frac{\alpha _i}{2\beta x_i^*(t)}\}= \min \{1,\frac{1}{2\beta }\}=\frac{1}{2\beta }$ for $i=i_1,\ldots , u$, $y_i(t)^{opt}=\min \{1,\frac{\alpha _i}{2\beta \frac{\alpha _i A_i}{2 \beta A_{i_k}} }\}= \min \{1,\frac{A_{i_m}}{A_i}\}=\frac{A_{i_m}}{A_i}$ for $i=u+1,\ldots , m-1$. Also, note that $x_m^*(t)\ge 0$. Now, if $x_m^*(t)> 0$, then $y_m(t)^{opt}=\min \{1,\frac{\alpha _i}{2\beta (W-\sum _{j=i_1}^{m-1} x^*_j(t))}\}= \min \{1,\frac{\alpha _i}{2\beta (W-\sum _{j=i_1}^{u} \alpha _j-\frac{\sum _{j=u+1}^{m-1} \alpha _j A_j }{2 \beta A_{m}})}\}=1$, as $W \le \sum _{j=i_1}^{u} \alpha _j+\frac{\sum _{j=u+1}^m \alpha _j A_j }{2 \beta A_{m}}$ by Condition 4. If $x_m^*(t)=0$, then agent $m$’s best response to $x_m^*(t)$ is given by (24), that is, $y_m(t)^{opt}=1$. Finally, as $x_i^*(t)=0$ for $i \in \{m+1, \ldots , i_{n(t)}\}$; for $i=m+1, \ldots , i_{n(t)}$, each agent’s best response to $x_i^*(t)$ is given by (24), that is, $y_i(t)^{opt}=1$. Hence, $y^*(t)$ is a best response to $x^*(t)$.

On the other hand, given $y^*(t)$,

$$\begin{aligned} A_i y^*_i(t)= \left\{ \begin{array}{llllll} &{} \frac{A_i}{2\beta } &{} \hbox { if } i=i_1,\ldots , u,\\ &{} A_{m} &{} \hbox { if } i=u+1,\ldots , m,\\ &{} A_i &{} \hbox { if } i= m+1,\ldots , i_{n(t)}.\\ \end{array} \right. \end{aligned}$$

(37)

By (14) and by Condition 2, $\frac{A_{i_1}}{2\beta }>\cdots >\frac{A_u}{2\beta }\ge A_{m}>\cdots >A_{i_n(t)}$.

So, a best response of the inspector to $y^*(t)$ is to allocate the maximum possible to each agent $i=i_1,\ldots ,u$, and the remainder of its budget to allocate randomly and feasibly among agents $i=u+1,\ldots , m$. In particular, $x^*(t)$ is a best response to $y^*(t)$. As $y^*(t)$ is a best response to $x^*(t)$, and $x^*(t)$ is a best response to $y^*(t)$, $(x^*(t),y^*(t))$ is a Nash equilibrium.

($C$):

Assume that there exists a $u \in \{i_{k-1}, i_{k-2}, \ldots , i_1, 0\}$ and an $m \in \{i_k, \ldots , i_{n(t)}\}$ such that conditions 1–5 of Case (C) are satisfied, and that $(x^*(t),y^*(t))$ satisfies (28) with $\lambda \equiv \sum _{j=u+1}^{m} \frac{\alpha _j A_j}{2\beta (W-\sum _{j=i_1}^{u} \alpha _j)}$.

We first show that $x^*(t)\in {\mathcal {X}}(t)$. For $i= i=u+1,\ldots , m$, $[x^*_i(t)=\frac{\alpha _i A_i}{2 \beta \lambda }\le \alpha _i]\Leftrightarrow [\frac{A_i}{2 \beta }\le \lambda ]$. By (14), $\frac{A_{m}}{2 \beta }<\cdots <\frac{A_{u+1}}{2\beta }$, so if $[\frac{A_{u+1}}{2 \beta }\le \lambda ]$, the latter inequality is satisfied. So, $[\frac{A_{u+1}}{2 \beta }\le \lambda ] \Leftrightarrow [\frac{A_{u+1}}{2 \beta }\le \sum _{j=u+1}^{m} \frac{\alpha _j A_j}{2\beta (W-\sum _{j=i_1}^{u} \alpha _j)}] \Leftrightarrow [W \le \sum _{j=i_1}^{u} \alpha _j+\frac{\sum _{j=u+1}^m \alpha _j A_j}{A_{u+1}}]$, which is Condition 3 of (C), and so it is satisfied. Further, $\sum _{j=i_1}^{m}x^*_j(t)=\sum _{j=i_1}^{u} \alpha _j+ \sum _{j=u+1}^{m} \frac{\alpha _j A_j}{2 \beta \lambda } = \sum _{j=i_1}^{u} \alpha _j+ \sum _{j=u+1}^{m} \frac{\alpha _j A_j}{2 \beta (\sum _{j=u+1}^{m} \frac{\alpha _j A_j}{2\beta (W-\sum _{j=i_1}^{u} \alpha _j)})}=W$. So, $x^*(t)\in {\mathcal {X}}(t)$.

We next show that $y^*(t)\in {\mathcal {Y}}(t)$. Clearly, as $\beta > \frac{1}{2}$, by Condition 1, $y_i^*(t)\le 1$ for $i=i_1,\ldots , u$. For $i=u+1,\ldots , m$, $[y_i^*(t)=\frac{\lambda }{A_i}\le 1]\Leftrightarrow [\lambda \le A_i]$. By (14), $A_m<\cdots <A_{u+1}$, so if $[\lambda \le A_{m}]$, the latter inequality is satisfied. So, $[\lambda \le A_{m}]\Leftrightarrow [W \ge \sum _{j=i_1}^{u} \alpha _j+\frac{\sum _{j=u+1}^m \alpha _j A_j}{2 \beta A_{m}}]$, which is Condition 4 of Case (C) and so it is satisfied. Finally, $y_i^*(t)=1$ for $i=m+1,\ldots ,i_{n(t)}$. So, $y^*(t)\in {\mathcal {Y}}(t)$.

Now, as $x_i^*(t)>0$ for $i \in \{i_1, \ldots , m\}$, each agent’s best response to $x_i^*(t)$ is given by (22). That is, $y_i(t)^{opt}=\min \{1,\frac{\alpha _i}{2\beta x_i^*(t)}\}= \min \{1,\frac{1}{2\beta }\}=\frac{1}{2\beta }$ for $i=i_1,\ldots , u$, and $y_i(t)^{opt}=\min \{1,\frac{\alpha _i}{2\beta \frac{\alpha _i A_i}{2 \beta \lambda }}\}= \min \{1,\frac{\lambda }{A_i}\}=\frac{\lambda }{A_i}$ for $i=u+1,\ldots , m$, as $\lambda \le A_{i_{k}}$ (see above). Finally, as $x_i^*(t)=0$ for $i \in \{m+1, \ldots , i_{n(t)}\}$, for $i=m+1, \ldots , i_{n(t)}$, each agent’s best response to $x_i^*(t)$ is given by (24). That is, $y_i(t)^{opt}=1$. Hence, $y^*(t)$ is a best response to $x^*(t)$.

On the other hand, given $y^*(t)$,

$$\begin{aligned} A_i y^*_i(t)= \left\{ \begin{array}{llllll} &{} \frac{A_i}{2\beta } &{} \hbox { if } i=i_1,\ldots , u,\\ &{} \lambda &{} \hbox { if } i=u+1,\ldots , m,\\ &{} A_i &{} \hbox { if } i= m+1,\ldots , i_{n(t)}.\\ \end{array} \right. \end{aligned}$$

(38)

Now, by (14), $\frac{A_{i_1}}{2\beta }>\cdots >\frac{A_u}{2\beta }$. Also, $[\frac{A_u}{2\beta }\ge \lambda ]\Leftrightarrow [\frac{A_u}{2\beta }\ge \sum _{j=u+1}^{m} \frac{\alpha _j A_j}{2\beta (W-\sum _{j=i_1}^{u} \alpha _j)}]\Leftrightarrow [W \ge \sum _{j=i_1}^{u} \alpha _j+\frac{\sum _{j=u+1}^k \alpha _j A_j }{A_{u}}]$, which is Condition 2 of Case (C) and so it is satisfied.

Further, by (14), $A_{m+1}>\cdots >A_{i_{n(t)}}$, so $[\lambda \ge A_{m+1}(>\cdots >A_{i_{n(t)}})] \Leftrightarrow [\sum _{j=u+1}^{m} \frac{\alpha _j A_j}{2\beta (W-\sum _{j=i_1}^{u} \alpha _j)}\ge A_{m+1}]\Leftrightarrow [W \le \sum _{j=i_1}^{u} \alpha _j+\frac{\sum _{j=u+1}^m \alpha _j A_j}{2 \beta A_{m+1}}]$, which is Condition 5 of (C) and so it is satisfied.

So, a best response of the inspector to $y^*(t)$ is to allocate the maximum possible to each agent $i=i_1,\ldots ,u$, and the remainder of its budget to allocate randomly and feasibly among agents $i=u+1,\ldots , m$. In particular, $x^*(t)$ is a best response to $y^*(t)$. As $y^*(t)$ is a best response to $x^*(t)$, and $x^*(t)$ is a best response to $y^*(t)$, $(x^*(t),y^*(t))$ is a Nash equilibrium. $\square$