Abstract
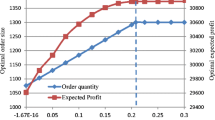
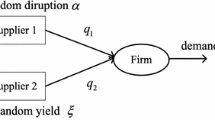
In this paper, we show how ordering time can be used as a mechanism to mitigate the supply risks of the unreliable newsboy. We consider the situation where a firm has an option of placing a series of sequential orders such that a new order is placed only after the yield from the previous order is known and derive an optimal order quantity for each ordering stage. The effectiveness of our approach is assessed by comparing its expected cost with the expected cost of the conventional reliable newsboy problem. It is demonstrated that the adverse effect of supply side risks can be almost completely negated by adopting our approach when the combined purchasing and holding costs for a low cost supplier at an earlier stage are equal to those of a high cost supplier at the next stage. Computational experiments suggest that the sequential ordering policy performs better than a simultaneous ordering strategy when customer service level norms become stringent and inventory holding costs decrease.



Similar content being viewed by others
References
Babich, V., Burnetas, A. N., & Ritchken, P. H. (2007). Competition and diversification effects in supply chains with supplier default risk. Manufacturing and Service Operations Management, 9(2), 123–146.
Burke, G. J., Carrillo, J. E., & Vakharia, A. J. (2007). Single versus multiple supplier sourcing strategies. European Journal of Operational Research, 182, 95–112.
Burke, G. J., Carrillo, J. E., & Vakharia, A. J. (2009). Sourcing decisions with stochastic supplier reliability and stochastic demand. Production and Operations Management, 18(4), 475–484.
Chao, X., Gong, X., & Zheng, S. (2014). Optimal pricing and inventory policies with reliable and random-yield suppliers: characterization and comparison. Annals of operations Research. doi:10.1007/s10479-014-1547-0.
Chen, W., Feng, Q., & Seshadri, S. (2013). Sourcing from suppliers with random yield for price-dependent demand. Annals of Operations Research, 208, 557–579. doi:10.1007/s10479-011-1046-5.
Dada, M., Petruzzi, N. C., & Schwarz, L. B. (2007). A newsvendor’s procurement problem when suppliers are unreliable. Manufacturing and Service Operations Management, 9(1), 9–32.
Federgruen, A., & Yang, N. (2009). Optimal supply diversification under general supply risks. Operations Research, 57(6), 1451–1468.
Federgruen, A., & Yang, N. (2011). Supply chain management under simultaneous supply and demand risks. In H. Gurnani, A. Mehrotra, & S. Ray (Eds.), Supply chain disruptions: Theory and practice of managing risk. London: Springer.
Gerchak, Y. (1996). A newsvendor with multiple, unreliable, all or- nothing suppliers. Working paper. Waterloo, ON: University of Waterloo.
Gerchak, Y., Vickson, R. G., & Parlar, M. (1988). Periodic review production models with variable yield and uncertain demand. IIE Transactions, 20(2), 144–150.
Grosfeld-Nir, A., & Gerchak, Y. (1996). Production to order with random yields: Single-stage multiple lot sizing. IIE Transactions, 28, 669–676.
Grosfeld-Nir, A., & Gerchak, Y. (2004). Multiple lot-sizing in production to order with random yields: Review of recent advances. Annals of Operations Research, 126, 43–69.
Gurnani, H., Akella, R., & Lehoczky, J. (1996). Optimal order policies in assembly systems with random demand and random supplier delivery. IIE Transactions, 28, 865–878.
Guu, S.-M., & Zhang, A. X. (2003). The finite multiple lot sizing problem with interrupted geometric yield and holding costs. European Journal of Operational Research, 145(3), 635–644.
Hammond, J. H., & Raman, A. (1994). Sport Obermeyer Ltd. HBR case study no. 695022.
Henig, M., & Gerchak, Y. (1990). The structure of periodic review policies in the presence of random yield. Operations Research, 38(4), 634–642.
Inderfurth, K. (2004). Analytical solution for a single-period production-inventory problem with uniformly distributed yield and demand. Central European Journal of Operations Research, 12, 117–127.
Jones, P. C., Lowe, T. J., Traub, R. D., & Kegler, G. (2001). Matching supply and demand: The value of a second chance in producing hybrid seed corn. Manufacturing and Service Operations Management, 3, 122–137.
Kazaz, B. (2004). Production planning under yield and demand uncertainty with yield-dependent cost and price. Manufacturing and Service Operations Management, 6(3), 209–224.
Leidy, M. P. (1992). Hedging across suppliers under stochastic input deliveries. Economic Notes, 21, 39–59.
Merzifonluoglu, Y., & Feng, Y. (2013). Newsboy problem with multiple unreliable suppliers. International Journal of Production Research. doi:10.1080/00207543.2013.835497.
Ozekici, S., & Parlar, M. (1999). Inventory models with unreliable suppliers in a random environment. Annals of Operations Research, 91, 123–136.
Parlar, M., & Wang, D. (1993). Diversification under yield randomness in inventory models. European Journal of Operational Research, 66, 52–64.
Parlar, M., Wang, Y., & Gerchak, Y. (1995). A periodic review inventory model with Markovian supply availability. International Journal of Production Economics, 42(2), 131–136.
Qin, Y., Wang, R., Vakharia, A. J., Chen, Y., & Seref, M. (2010). The newsvendor problem: Review and directions for future research. European Journal of Operational Research. doi:10.1016/j.ejor.2010.11.024.
Rekik, Y., Sahin, E., & Dallery, Y. (2007). A comprehensive analysis of the newsvendor model with unreliable supply. OR Spectrum, 29(2), 207–233.
Stecke, K., & Kumar, S. (2009). Sources of supply chain disruptions, factors that breed vulnerability, and mitigating strategies. Journal of Marketing Channels, 16(3), 193–226.
Tiwari, D., Patil, R., & Shah, J. (2011). Unreliable newsboy problem with a forecast update. Operations Research letters, 39, 278–282.
Tomlin, B., & Wang, Y. (2005). On the value of mix-flexibility and dual sourcing in Unreliable newsvendor networks. Manufacturing and Service Operations Management, 7(1), 37–57.
Tomlin, B. (2009). The impact of supply learning when suppliers are unreliable. Manufacturing and Service Operations Management, 11(2), 192–209.
Turnbull, G. K. (1986). Theory of the firm under the threat of input supply interruption. Southern Economic Journal, 53, 807–817.
Yano, C. A., & Lee, H. L. (1995). Lot sizing with random yield: A review. Operations Research, 43(2), 311–334.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
Proof of Theorem 4
Assuming the opening inventory is zero and that the demand is uniformly distributed between 0 and \(a\).
Using Eqs. (3), (4) and (5), and also assuming opening inventory at stage 2 to be zero \(I_{2}\) = 0
Also for uniformly distributed demand, \(f(x)=\frac{1}{a}\hbox { and } F(x)=\frac{x}{a},\;K_1 =a\left[ {\frac{p-c_1 }{p+v}} \right] ,\quad \alpha =\frac{a}{2}\).
Substituting in the expected cost expression,
Expected cost for newsboy problem
Also optimal \(q_1 =K_1 \hbox { where }K_1 =F^{-1}\left[ {\left( {p-c_1 } \right) /\left( {p+v} \right) } \right] \).
As demand is uniformly distributed between 0 to \(a, \therefore \quad f(x)=\frac{1}{a} ,F(x)=\frac{x}{a}\).
Similarly it can be shown that for 3-stage sequential ordering:
And for n stages,
Proof of Lemma 1
For two simultaneous orders, the expected cost can be written as :
Algebraic processing of the above equation yields following expected cost expression
Equating the differentiations of the equation with respect to \(q_1\) and \(q_2\) to zero gives
Processing of the above equation gives
Similarly,
Substituting \(q_2^*\, in \,q_1^*\) gives
Similarly,
Let \(p_1 =\left( {p-c_1 } \right) \) and \(p_2 =\left( {p-c_2 } \right) \) and \(\frac{1}{X}=\frac{a}{\left( {p+v} \right) }\).
Initially substituting with these terms in the expected cost expression and algebraic processing yields the following optimal expected cost expression
Rights and permissions
About this article
Cite this article
Tiwari, D., Patil, R. & Shah, J. Sequential unreliable newsboy ordering policies. Ann Oper Res 233, 449–463 (2015). https://doi.org/10.1007/s10479-014-1705-4
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10479-014-1705-4