Value of information for a leader–follower partially observed Markov game

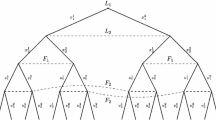
Abstract

We consider a leader–follower partially observed Markov game (POMG) and analyze how the value of the leader’s criterion changes due to changes in the leader’s quality of observation of the follower. We give conditions that insure improved observation quality will improve the leader’s value function, assuming that changes in the observation quality do not cause the follower to change its policy. We show that discontinuities in the value of the leader’s criterion, as a function of observation quality, can occur when the change of observation quality is significant enough for the follower to change its policy. We present conditions that determine when a discontinuity may occur and conditions that guarantee a discontinuity will not degrade the leader’s performance. We show that when the leader and the follower are collaborative and the follower completely observes the leader’s initial state, discontinuities in the leader’s value function will not occur. However, examples show that improving observation quality does not necessarily improve the leader’s criterion value, whether or not the POMG is a collaborative game.

Appendices

Appendix 1: Proofs

Proof of Theorem 1

Proof of Theorem 1 is given in White and Harrington (1980).$\square$

Proof of Corollary 1

Proof of (a) follows from the fact that an optimal policy has a concave value function and can be found in White and Harrington (1980) and Zhang (2010). Proof of (b) follows from the facts that for any stochastic matrix $Q'$, there are stochastic matrices R and $R''$ such that $Q'R = Q$ and $Q''R'' = Q'$. $\square$

Proof of Proposition 1

Proof follows the proof of Proposition 2 in Chang et al. (2014). $\square$

Proof of Proposition 2

Proof follows from Lemma 1 in Ortiz et al. (2013) and Proposition 2 in Chang et al. (2014). $\square$

Proof of Corollary 2

(1) follows directly from Theorem 1 and Proposition 1. It is sufficient to show that $v^L(\pi ^L, \pi ^F, Q)(d^L(t,\tau ), y^L(t))$ is concave in $y^L(t)$ for (2) to hold. It follows from Proposition 2 that

$$\begin{aligned}&v^L(\pi ^L, \pi ^F, Q)(d^L(t,\tau ), y^L(t)) \\&\quad = \max _{\rho ^L} \sum _{d^F(t,\tau )}P(d^F(t,\tau )|d^L(t)) g^L(d(t,\tau ), \rho ^L, \pi ^*(\rho ^L, Q),Q), \end{aligned}$$

which is concave in $y^L(t)$. $\square$

Proof of Proposition 3

For any scalar valued function v dependent on $(d(t,\tau ))$, define

$$\begin{aligned}&[Hv](d(t,\tau )) = R^L(d(t,\tau ),\pi ^L, \pi ^F) \\&\quad +\beta \sum _{\varsigma (t+1)} P(\varsigma (t+1)|d(t,\tau ), \pi ^L, \pi ^F,Q) \times v(\{\varsigma (t+1), d(t,\tau -1)\}). \end{aligned}$$

Define $H'$ identically to H but replace Q by $Q'$, where we note:

$$\begin{aligned}&P(\varsigma (t+1)|d(t,\tau ),\pi ^L, \pi ^F,Q) \\&\quad = \sum _{a(t)}P(a(t)|d(t,\tau ))P(z^L(t+1)|s^F(t+1))P(z^F(t+1), s(t+1)|s(t),a(t)). \end{aligned}$$

Let g and $g'$ be the fixed points of H and $H'$, respectively [Existence and uniqueness of these fixed points are assured by Theorem 6.2.3 in Puterman (1994)]. Then,

$$\begin{aligned}&g(d(t,\tau )) \!-\! g'(d(t,\tau ))\!=\! [Hg](d(t,\tau )) - [H'g'](d(t,\tau )) \!-\! [Hg'](d(t,\tau )) \!+ \)\\&\quad =\beta \sum _{a(t)}P(a(t)|d(t,\tau )) \times X, \end{aligned}$$

where

$$\begin{aligned} X&=\sum _{z(t+1)}\sum _{s(t+1)}P(z(t+1),s(t+1)|s(t),a(t))\\&\quad \times \{g(\{\varsigma (t+1), d(t,\tau -1)\})-g'(\{\varsigma (t+1), d(t,\tau -1)\})\}\\&\quad +\sum _{z(t+1)}\sum _{s(t+1)}[P(z^L(t+1)|s^F(t+1))-P'(z^L(t+1)|s^F(t+1))]P(z^F(t+1),\\&\qquad s(t+1)|s(t), a(t))\times g'(\{\varsigma (t+1), d(t,\tau -1)\}) \end{aligned}$$

Note, $||g'|| \le \frac{M}{1-\beta }$, where $M = \max _{s}\max _a r^L(s,a)$. Then, it is straightforward to show that

$$\begin{aligned} ||g-g'|| \le \beta ||g-g'|| + \beta ||Q-Q'||\frac{M}{1-\beta } \end{aligned}$$

and hence,

$$\begin{aligned} ||g-g'|| \le \frac{\beta M}{(1-\beta )^2}||Q-Q'||. \end{aligned}$$

$\square$

Proof of Proposition 4

If Q is such that

$$\begin{aligned} v^F(\pi ^L, \pi ^F, Q)(d^F(0)) - v^F(\pi ^L, \rho ^F, Q)(d^F(0)) \ge 0 \end{aligned}$$

for all $\rho ^F \ne \pi ^F, \rho ^F, \pi ^F \in \Pi ^F$ and given $d^F(0)$, then $Q \in K(\pi ^L, \pi ^F)$. Note

$$\begin{aligned}&v^F(\pi ^L, \pi ^F, Q)(d^F(0)) - v^F(\pi ^L, \rho ^F, Q)(d^F(0))\\&\quad = v^F(\pi ^L, \pi ^F, Q)(d^F(0)) - v^F(\pi ^L, \pi ^F, Q')(d^F(0)) + v^F(\pi ^L, \rho ^F, Q')(d^F(0)) \\&\qquad - v^F(\pi ^L, \rho ^F, Q)(d^F(0)) + v^F(\pi ^L, \pi ^F, Q')(d^F(0)) - v^F(\pi ^L, \rho ^F, Q')(d^F(0)) \\&\quad \ge -\frac{2\beta M}{(1-\beta )^2} ||Q-Q'||+b, \end{aligned}$$

where the inequality follows from Proposition 3 and definitions of b and M. The result follows from the fact that $b -\frac{2\beta M}{(1-\beta )^2} ||Q-Q'|| \ge 0$ if and only if $||Q-Q'||\le \frac{b(1-\beta )^2}{2\beta M}$. $\square$

Proof of Lemma 1

The proof follows from Proposition 4.7.3 (Puterman, p. 106) and a standard limit procedure. $\square$

Proof of Proposition 5

Lemma 1 guarantees that $g^L(d^L(t,\tau ), Q^*, \pi ^L, \pi ')$ for $\pi ' \!\in \! \{\pi ^F, \rho ^F\}$ is isotone in $d(t,\tau )$. It follows from Lemma 4.7.2 (Puterman, p. 106) that

$$\begin{aligned}&\sum _{\varsigma (t+1)} P(\varsigma (t+1)|d(t,\tau ), Q^*, \pi ^L, \rho ^F) \times g^L(d(t,\tau )| Q^*, \pi ^L, \pi ^F) \\&\quad \ge \sum _{\varsigma (t+1)} P(\varsigma (t+1)|d(t,\tau ), Q^*, \pi ^L, \pi ^F) \times g^L(d(t,\tau )| Q^*, \pi ^L, \pi ^F). \end{aligned}$$

Thus,,

$$\begin{aligned}&g^L(d(t,\tau ), Q^*, \pi ^L, \pi ^F) \nonumber \\&\quad \le R^L(d(t,\tau ), \pi ^L, \rho ^F) +\beta \sum _{\varsigma (t+1)} P (\varsigma (t+1)|Q^*, \pi ^L, \rho ^F) \times g^L(d(t,\tau ), Q^*, \pi ^L, \pi ^F). \end{aligned}$$

(6)

Let

$$\begin{aligned}&[Hv](d(t,\tau )) \\&\quad = R^L(d(t,\tau ), \pi ^L, \rho ^F) + \beta \sum _{\varsigma (t+1)}P(\varsigma (t+1)|d(t,\tau ), Q^*, \pi ^L, \rho ^F)\\&\quad \times v(\{\varsigma (t+1), d(t,\tau -1)\}). \end{aligned}$$

Define the sequence $\{v^n\}$ as $v^{n+1} = Hv^n$, where $v^0(d(t,\tau )) = g^L(d(t,\tau ), Q^*, \pi ^L, \pi ^F)$. We remark that $\lim _{n \rightarrow \infty } ||v^n - v^*|| = 0$, where $v^*(d(t,\tau )) = g^L(d(t,\tau ), Q^*, \pi ^L, \rho ^F).$ It is straightforward to show that $v \le v'$ implies $Hv \le Hv'$. Eq. (6) has shown $v^0 \le v^1$. Lemma 1 guarantees that $v^n$ is isotone in $d(t,\tau )$ for $n \ge 1$. Hence, by induction, $v^n \le v^{n+1}$ and therefore $v^n \le v^*$ for all n. Thus, $g^L(d(t,\tau ), Q^*, \pi ^L, \pi ^F) \le g^L(d(t,\tau ), Q^*, \pi ^L, \rho ^F)$ for all $d(t,\tau )$ and hence $v^L(\pi ^L, \pi ^F, Q^*)(d^L(0)) \le v^L(\pi ^L, \rho ^F, Q^*)(d^L(0))$. $\square$

Proof of Proposition 6

Assumption (1) implies that $v^F(\pi ^L, \pi ', Q^*)(d^F(0)) = g^F(d(0,\tau ), Q^*, \pi ^L, \pi ')$ for $\pi ' \in \{\pi ^F, \rho ^F \}.$ Assumption (2) implies $v^F(\pi ^L, \pi ^F, Q^*)(d^F(0)) = v^F(\pi ^L, \rho ^F, Q^*)(d^F(0))$. Hence, $g^F(d(0,\tau ), \pi ^L, \pi ^F)=g^F(d(0,\tau ), \pi ^L, \rho ^F)$. Assumption (3) implies $g^L=g^F$. $\square$

Appendix 2: Parameters for the examples

The parameters in Example 1 are:

• transition probabilities:

  $$\begin{aligned} P^L(1)= & {} \begin{bmatrix} 0.6229&0.3771\\ 0.7506&0.2494 \end{bmatrix}, P^L(2)=\begin{bmatrix} 0.7531&0.2469\\ 0.1761&0.8239 \end{bmatrix}\\ P^F(1)= & {} \begin{bmatrix} 0.2232&0.7768\\ 0.5131&0.4869 \end{bmatrix}, P^F(2)=\begin{bmatrix} 0.9449&0.0551\\ 0.2663&0.7337 \end{bmatrix} \end{aligned}$$

• reward structure $r^k(s^L,s^F,a^L,a^F), k \in \{L,F\}$:

  

  • (1) example(a):

    

  • (2) example(b):

    

  • (3) example(c):

    

  • (4) example(d):

    

  • (5) example(e):

    

  • (6) example(f):

    

The parameters in Example 2 are:

• transition probabilities: $P(s(t+1),z^F(t+1)|s(t),\pi ^L, \rho ^F)=$

  

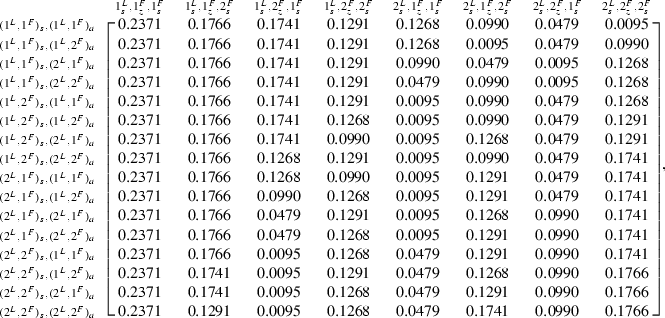
  $P(s(t+1),z^F(t+1)|s(t),\pi ^L, \pi ^F)=$

  
  $$\begin{aligned} Q^{L*} \in K(\pi ^L, \pi ^F) \cap K(\pi ^L, \rho ^F), Q^{L*}=\begin{bmatrix} 0.6&0.4\\ 0.4&0.6 \end{bmatrix} \end{aligned}$$

• reward structure: $R^F(d^F(t,\tau ),\pi ^L,\rho ^F)=[2.0944, -10, 9.1798, -10, 9.1768, -10, 9.1858,$ $-10,-10, 9.3521, -10, 9.3522, -10, 9.3620, -10, 2.8030]$ $R^F(d^F(t,\tau ),\pi ^L,\pi ^F)=[3.3540, 10, -9.3656, 10, -9.3656, 10, -9.3656, 10,$ $10, -9.3656, 10, -9.3656, 10, -9.3656, 10, -9.3656]$ $R^F(d^F(t,\tau ),\rho ^L,\rho ^{F'}) = -\infty , \forall \rho ^{F'} \in \Pi ^F$ $R^L(d^F(t,\tau ),\pi ^L,\rho ^F)=[2.9118,2.8947, 2.8725, 2.8715, 2.7401, 2.7174, 2.4442, 2.4008,$ 1.8971, 1.6406, 1.4561, 0.8355, 0.4728, 0.4257, 0.3810, 0.2926] $R^L(d^F(t,\tau ),\pi ^L,\pi ^F)=[2.0224, 1.9607, 1.9596, 1.9568, 1.9523, 1.9479, 1.7010, 1.6948,$ 1.2183, 0.9849, 0.8006, 0.4137, 0.3452, 0.2608, 0.2545, 0.0806]

The parameters in Example 3 are:

• (1) example(a):

  • transition probabilities:

    $$\begin{aligned} P^L(1)= & {} \begin{bmatrix} 0.3202&0.6798\\ 0.3044&0.6956 \end{bmatrix}, P^L(2)=\begin{bmatrix} 0.7624&0.2376\\ 0.3790&0.6210 \end{bmatrix}\\ P^F(1)= & {} \begin{bmatrix} 0.2593&0.7407\\ 0.6356&0.3644 \end{bmatrix}, P^F(2)=\begin{bmatrix} 0.5221&0.4779\\ 0.0994&0.9006 \end{bmatrix} \end{aligned}$$

  • reward structure $r^k(s^L,s^F,a^L,a^F), k \in \{L,F\}$:

    

• (2) example(b):

  • transition probabilities:

    $$\begin{aligned} P^L(1)= & {} \begin{bmatrix} 0.3277&0.6723\\ 0.9623&0.0377 \end{bmatrix}, P^L(2)=\begin{bmatrix} 0.4723&0.5277\\ 0.4469&0.5531 \end{bmatrix}\\ P^F(1)= & {} \begin{bmatrix} 0.8815&0.1185\\ 0.6147&0.3853 \end{bmatrix}, P^F(2)=\begin{bmatrix} 0.0641&0.9359\\ 0.2062&0.7938 \end{bmatrix} \end{aligned}$$

  • reward structure $r^k(s^L,s^F,a^L,a^F), k \in \{L,F\}$:

    

• (3) example(c):

  • transition probabilities:

    $$\begin{aligned} P^L(1)= & {} \begin{bmatrix} 0.7657&0.2343\\ 0.9270&0.0730 \end{bmatrix}, P^L(2)=\begin{bmatrix} 0.5570&0.4430\\ 0.8113&0.1887 \end{bmatrix}\\ P^F(1)= & {} \begin{bmatrix} 0.3594&0.6406\\ 0.0007&0.9993 \end{bmatrix}, P^F(2)=\begin{bmatrix} 0.4647&0.5353\\ 0.7964&0.2036 \end{bmatrix} \end{aligned}$$

  • reward structure $r^k(s^L,s^F,a^L,a^F), k \in \{L,F\}$:

    

• (4) example(d):

  • transition probabilities:

    $$\begin{aligned} P^L(1)= & {} \begin{bmatrix} 0.5983&0.4017\\ 0.6592&0.3408 \end{bmatrix}, P^L(2)=\begin{bmatrix} 0.8785&0.1215\\ 0.3068&0.6932 \end{bmatrix}\\ P^F(1)= & {} \begin{bmatrix} 0.7036&0.2964\\ 0.5885&0.4115 \end{bmatrix}, P^F(2)=\begin{bmatrix} 0.0593&0.9407\\ 0.3593&0.6407 \end{bmatrix} \end{aligned}$$

  • reward structure $r^k(s^L,s^F,a^L,a^F), k \in \{L,F\}$: