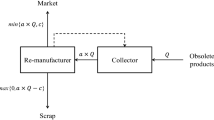
Abstract
As an effective mode for resource recovery, remanufacturing has been widely recognized in practice and academia. However, coordination is needed and multi-uncertainties exist in a remanufacturing supply chain (RSC). Under a retailer collection mode, this paper extends the existing studies on a revenue-sharing mechanism for a forward supply chain to examine how to coordinate a RSC between a remanufacturer and a retailer by developing a mathematical model. This model considers two types of uncertainties, they are, the stochastic remanufacturability rate from the supply side of used products and the random demand occurring in remarketing of remanufactured products. This study fills the research gap on RSC coordination under the multi-uncertainty environment. Moreover, it introduces an iterative algorithm (the Newton–Raphson Method) to deal with difficulty in solving the implicit function of the payment to consumers under the non-uniform demand distribution by finding the approximate value. The research results show that a revenue-sharing contract for a RSC with multi-uncertainties can increase profit for the whole RSC as well as the remanufacturer and the retailer by eliminating double marginalization. Besides, the government subsidy to the remanufacturer can motivate the retailer to collect more used products under a revenue-sharing case since the retailer can share benefits of the whole RSC. A case study of remanufactured truck engines demonstrates benefits of the proposed revenue-sharing mechanism and the profit increase for the whole RSC with the government subsidy.









Similar content being viewed by others
Notes
It is abbreviated as JFP. http://www.chinajfp.com/ (or http://en.chinajfp.com/ for English Version).
1 CNY = 0.163 USD or 1 USD = 6.1347 CNY at 19/09/2014.
References
Anupindi, R., & Akella, R. (1993). Diversification under supply uncertainty. Management Science, 39(8), 944–963. doi:10.1287/mnsc.39.8.944.
Arshinder, S., Kanda, A., & Deshmukh, S. G. (2008). Supply chain coordination: Perspectives, empirical studies and research directions. International Journal of Production Economics, 115(2), 316–335. doi:10.1016/j.ijpe.2008.05.011.
Atasu, A., & Souza, G. C. (2013). How does product recovery affect quality choice? Production and Operations Management, 22(4), 991–1010. doi:10.1111/j.1937-5956.2011.01290.x.
Bakal, I. S., & Akcali, E. (2006). Effects of random yield in remanufacturing with price-sensitive supply and demand. Production and Operations Management, 15(3), 407–420.
Bresnahan, T. F., & Reiss, P. C. (1985). Dealer and manufacturer margins. Rand Journal of Economics, 16(2), 253–268. doi:10.2307/2555413.
Cachon, G. P. (2003). Supply chain coordination with contracts. In S. C. Graves & A. G. d Kok (Eds.), Handbooks in operations research and management science (Vol. 11, pp. 227–339). Amsterdam: Elsevier.
Cachon, G. P., & Lariviere, M. A. (2005). Supply chain coordination with revenue-sharing contracts: Strengths and limitations. Management Science, 51(1), 30–44. doi:10.1287/mnsc.1040.0215.
Cai, X. Q., Lai, M. H., Li, X., Li, Y. J., & Wu, X. Y. (2014). Optimal acquisition and production policy in a hybrid manufacturing/remanufacturing system with core acquisition at different quality levels. European Journal of Operational Research, 233(2), 374–382. doi:10.1016/j.ejor.2013.07.017.
Choi, T. M., & Cheng, T. C. E. (2011). Supply chain coordination under uncertainty. London: Springer Science & Business Media.
Choi, T. M., Li, D., & Yan, H. M. (2008). Mean-variance analysis of a single supplier and retailer supply chain under a returns policy. European Journal of Operational Research, 184(1), 356–376. doi:10.1016/j.ejor.2006.10.051.
Corbett, C. J., Zhou, D. M., & Tang, C. S. (2004). Designing supply contracts: Contract type and information asymmetry. Management Science, 50(4), 550–559. doi:10.1287/mnsc.1030.0173.
De Giovanni, P. (2014). Environmental collaboration in a closed-loop supply chain with a reverse revenue sharing contract. Annals of Operations Research, 220(1), 135–157. doi:10.1007/s10479-011-0912-5.
De Giovanni, P., & Roselli, M. (2012). Overcoming the drawbacks of a revenue-sharing contract through a support program. Annals of Operations Research, 196(1), 201–222. doi:10.1007/s10479-012-1113-6.
Dellarocas, C. (2012). Double marginalization in performance-based advertising: Implications and solutions. Management Science, 58(6), 1178–1195. doi:10.1287/mnsc.1110.1474.
Demirag, O. C. (2013). Performance of weather-conditional rebates under different risk preferences. Omega-International Journal of Management Science, 41(6), 1053–1067. doi:10.1016/j.omega.2013.02.001.
Galbreth, M. R., & Blackburn, J. D. (2006). Optimal acquisition and sorting policies for remanufacturing. Production and Operations Management, 15(3), 384–392.
Galbreth, M. R., & Blackburn, J. D. (2010). Optimal acquisition quantities in remanufacturing with condition uncertainty. Production and Operations Management, 19(1), 61–69. doi:10.3401/poms.1080.01067.
Gatilov, S. Y. (2014). Using low-rank approximation of the Jacobian matrix in the Newton–Raphson method to solve certain singular equations. Journal of Computational and Applied Mathematics, 272, 8–24. doi:10.1016/j.cam.2014.04.024.
Gerchak, Y., & Wang, Y. Z. (2004). Revenue-sharing vs. wholesale-price contracts in assembly systems with random demand. Production and Operations Management, 13(1), 23–33.
Govindan, K., & Popiuc, M. N. (2014). Reverse supply chain coordination by revenue sharing contract: A case for the personal computers industry. European Journal of Operational Research, 233(2), 326–336. doi:10.1016/j.ejor.2013.03.023.
Govindan, K., Popiuc, M. N., & Diabat, A. (2013). Overview of coordination contracts within forward and reverse supply chains. Journal of Cleaner Production, 47, 319–334. doi:10.1016/j.jclepro.2013.02.001.
Guide, V. D. R, Jr, Teunter, R. H., & Van Wassenhove, L. N. (2003). Matching demand and supply to maximize profits from remanufacturing. Manufacturing & Service Operations Management, 5(4), 303–316.
Guide, V. D. R., & Van Wassenhove, L. N. (2001). Managing product returns for remanufacturing. Production and Operations Management, 10(2), 142–155.
Hasanov, P., Jaber, M. Y., & Zolfaghari, S. (2012). Production, remanufacturing and waste disposal models for the cases of pure and partial backordering. Applied Mathematical Modelling, 36(11), 5249–5261. doi:10.1016/j.apm.2011.11.066.
He, Y., & Zhao, X. (2012). Coordination in multi-echelon supply chain under supply and demand uncertainty. International Journal of Production Economics, 139(1), 106–115. doi:10.1016/j.ijpe.2011.04.021.
Heckmann, I., Comes, T., & Nickel, S. (2015). A critical review on supply chain risk: Definition, measure and modeling. Omega-International Journal of Management Science, 52, 119–132.
Hu, F., Lim, C. C., & Lu, Z. D. (2013). Coordination of supply chains with a flexible ordering policy under yield and demand uncertainty. International Journal of Production Economics, 146(2), 686–693. doi:10.1016/j.ijpe.2013.08.024.
Lariviere, M. A., & Porteus, E. L. (2001). Selling to the newsvendor: An analysis of price-only contracts. Manufacturing & service operations management, 3(4), 293–305.
Lee, C. H., Rhee, B. D., & Cheng, T. C. E. (2013). Quality uncertainty and quality-compensation contract for supply chain coordination. European Journal of Operational Research, 228(3), 582–591. doi:10.1016/j.ejor.2013.02.027.
Lee, H. L., So, K. C., & Tang, C. S. (2000). The value of information sharing in a two-level supply chain. Management Science, 46(5), 626–643. doi:10.1287/mnsc.46.5.626.12047.
Li, X., Li, Y. J., & Cai, X. Q. (2013). Double marginalization and coordination in the supply chain with uncertain supply. European Journal of Operational Research, 226(2), 228–236. doi:10.1016/j.ejor.2012.10.047.
Li, X., Li, Y. J., & Cai, X. Q. (2015). Remanufacturing and pricing decisions with random yield and random demand. Computers & Operations Research, 54, 195–203. doi:10.1016/j.cor.2014.01.005.
Lian, Z. T., & Deshmukh, A. (2009). Analysis of supply contracts with quantity flexibility. European Journal of Operational Research, 196(2), 526–533. doi:10.1016/j.ejor.2008.02.043.
Liu, S. S., Shah, N., & Papageorgiou, L. G. (2012). Multiechelon supply chain planning with sequence-dependent changeovers and price elasticity of demand under uncertainty. Aiche Journal, 58(11), 3390–3403. doi:10.1002/Aic.13732.
Mafakheri, F., & Nasiri, F. (2013). Revenue sharing coordination in reverse logistics. Journal of Cleaner Production, 59, 185–196. doi:10.1016/j.jclepro.2013.06.031.
Mishra, B. K., Raghunathan, S., & Yue, X. H. (2009). Demand forecast sharing in supply chains. Production and Operations Management, 18(2), 152–166. doi:10.3401/poms.1080.01013.
Mukhopadhyay, S. K., & Ma, H. F. (2009). Joint procurement and production decisions in remanufacturing under quality and demand uncertainty. International Journal of Production Economics, 120(1), 5–17. doi:10.1016/j.ijpe.2008.07.032.
Nenes, G., Panagiotidou, S., & Dekker, R. (2010). Inventory control policies for inspection and remanufacturing of returns: A case study. International Journal of Production Economics, 125(2), 300–312. doi:10.1016/j.ijpe.2010.02.008.
Ouyang, Y. F. (2006). Characterization of the bullwhip effect in, linear, time-invariant supply chains: Some formulae and tests. Management Science, 52(10), 1544–1556. doi:10.1287/mnsc.1060.0573.
Ozelkan, E. C., & Lim, C. (2008). Conditions of reverse bullwhip effect in pricing for price-sensitive demand functions. Annals of Operations Research, 164(1), 211–227. doi:10.1007/s10479-008-0444-9.
Pasternack, B. A. (1985). Optimal pricing and return policies for perishable commodities. Marketing Science, 4(2), 166–176.
Peidro, D., Mula, J., Poler, R., & Lario, F. C. (2009). Quantitative models for supply chain planning under uncertainty: A review. International Journal of Advanced Manufacturing Technology, 43(3–4), 400–420.
Sasikumar, P., Kannan, G., & Haq, A. N. (2010). A multi-echelon reverse logistics network design for product recovery: A case of truck tire remanufacturing. International Journal of Advanced Manufacturing Technology, 49(9–12), 1223–1234. doi:10.1007/s00170-009-2470-4.
Savaskan, R. C., Bhattacharya, S., & Van Wassenhove, L. N. (2004). Closed-loop supply chain models with product remanufacturing. Management Science, 50(2), 239–252. doi:10.1287/mnsc.1030.0186.
Savaskan, R. C., & Van Wassenhove, L. N. (2006). Reverse channel design: The case of competing retailers. Management Science, 52(1), 1–14. doi:10.1287/mnsc.1050.0454.
Seifert, R. W., Zequeira, R. I., & Liao, S. Q. (2012). A three-echelon supply chain with price-only contracts and sub-supply chain coordination. International Journal of Production Economics, 138(2), 345–353. doi:10.1016/j.ijpe.2012.04.006.
Sheu, J. B. (2011). Bargaining framework for competitive green supply chains under governmental financial intervention. Transportation Research Part E-Logistics And Transportation Review, 47(5), 573–592. doi:10.1016/j.tre.2010.12.006.
Simangunsong, E., Hendry, L. C., & Stevenson, M. (2012). Supply-chain uncertainty: A review and theoretical foundation for future research. International Journal of Production Research, 50(16), 4493–4523. doi:10.1080/00207543.2011.613864.
Spengler, J. J. (1950). Vertical integration and antitrust policy. The Journal of Political Economy, 347–352.
Sridharan, U. V., Caines, W. R., & Patterson, C. C. (2005). Implementation of supply chain management and its impact on the value of firms. Supply Chain Management: An International Journal, 10(3–4), 313–318. doi:10.1108/13598540510612785.
Taylor, T. A. (2002). Supply chain coordination under channel rebates with sales effort effects. Management Science, 48(8), 992–1007. doi:10.1287/mnsc.48.8.992.168.
Tomlin, B. (2006). On the value of mitigation and contingency strategies for managing supply chain disruption risks. Management Science, 52(5), 639–657. doi:10.1287/mnsc.11060.0515.
Tsay, A. A. (1999). The quantity flexibility contract and supplier-customer incentives. Management Science, 45(10), 1339–1358. doi:10.1287/mnsc.45.10.1339.
Wang, F., & Choi, I. C. (2014). Optimal Decisions in a Single-Period Supply Chain with Price-Sensitive Random Demand under a Buy-Back Contract. Mathematical Problems in Engineering.
Yang, C. H., Wang, J., & Ji, P. (2015). Optimal acquisition policy in remanufacturing under general core quality distributions. International Journal of Production Research, 53(5), 1425–1438. doi:10.1080/00207543.2014.944283.
Zhang, Q. H., Dong, M., Luo, J. W., & Segerstedt, A. (2014). Supply chain coordination with trade credit and quantity discount incorporating default risk. International Journal of Production Economics, 153, 352–360. doi:10.1016/j.ijpe.2014.03.019.
Zhang, Y., Vovk, V., & Zhang, W. G. (2014b). Probability-free solutions to the non-stationary newsvendor problem. Annals of Operations Research, 223(1), 433–449.
Zhou, S. X., & Yu, Y. K. (2011). Optimal product acquisition, pricing, and inventory management for systems with remanufacturing. Operations Research, 59(2), 514–521.
Zhou, X., & Huo, J. Z. (2010). Coordinating ordering and production polices for JIT: Bargain power analysis. Proceedings of 2010 international conference on logistics systems and intelligent management, Vols 1--3, 1--5.
Zissis, D., Ioannou, G., & Burnetas, A. (2015). Supply chain coordination under discrete information asymmetries and quantity discounts. Omega, 53, 21–29.
Zou, X. X., Pokharel, S., & Piplani, R. (2008). A two-period supply contract model for a decentralized assembly system. European Journal of Operational Research, 187(1), 257–274. doi:10.1016/j.ejor.2007.03.011.
Acknowledgments
This work is supported by grants from the National Key Basic Research Program of China (973 Program, 2011CB013406), National Science Fund for Distinguished Young Scholars (71025002), National Natural Science Foundation of China (71472021), and the Major Program of the National Social Science Fund of China (13&ZD147). The authors express their gratitude to Huan LIU in JFP and Jun-hao YAN in Zhengzhou maintenance station for their help for site visits. This study also thanks He-long LI, Huan-yun LI and Na LI for their help on data collection of truck engines.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: The list of symbols used in the paper
Expected profit:
- \(\prod _r^D \) :
-
retailer’s expected profit in decentralized case (wholesale-case)
- \(\prod _m^D \) :
-
remanufacturer’s expected profit in decentralized case (wholesale-case)
- \(\prod _{SC}^D \) :
-
supply chain’s expected profit in decentralized case (wholesale-case)
- \(\prod _r^C \) :
-
retailer’s expected profit in centralized case
- \(\prod _m^C \) :
-
remanufacturer’s expected profit in centralized case
- \(\prod _{SC}^C \) :
-
supply chain’s expected profit in centralized case
- \(\prod _r^{RS} \) :
-
retailer’s expected profit under revenue-sharing contract
- \(\prod _m^{RS} \) :
-
remanufacturer’s expected profit under revenue-sharing contract
- \(\prod _{SC}^{RS} \) :
-
supply chain’s expected profit under revenue-sharing contract
Uncertainty factors (Stochastic variables):
- \(\xi \) :
-
the remanufacturablity rate, and it is a percentage of used products that can be remanufactured. It is a stochastic variable and the distribution is known
- \(E(\xi )\) :
-
the expectation of remanufacturablity rate \(\xi \)
- D :
-
the demand for remanufactured products, and it is a stochastic variable. CDF of D is F(x), PDF of D is f(x), expectation of D is \(E(D)=\mu \). \(F^{-1}(x)\) is the inverse distribution function of F(D)
For retailer:
- \(p_r \) :
-
unit price to consumers for used products acquisition
- \(p_r^D \) :
-
optimal unit price to consumers for used products acquisition in decentralized case
- \(p_r^C \) :
-
optimal unit price to consumers for used products acquisition in centralized case
- \(w^{d}\) :
-
transfer payment charged by a retailer on a remanufacturer per used product
- \(c_{ri} \) :
-
unit inventory cost in retailer’s location
- \(c_{rf} \) :
-
unit freight cost from a retailer to a remanufacturer
- q :
-
the quantity of remanufactured products delivered from a remanufacturer, and it rely on \(\xi \)
- \(c_{rh} \) :
-
handing cost of selling product at the retailer
For remanufacturer:
- P :
-
selling price of remanufactured products
- \(c_{me} \) :
-
unit examination cost at a remanufacturer, when used products are transported to remanufacturer, it would be examined to check whether it can be remanufactured or not
- \(c_{ms} \) :
-
unit sorting cost by the remanufacturer (including dismantling cost)
- \(c_{mr} \) :
-
unit remanufacturing cost (including testing cost)
- \(c_{md} \) :
-
unit disposal cost, for used products that cannot be remanufactured, it suffers a cost of disposal fee
- \(c_{mi} \) :
-
unit inventory cost during holding at the remanufacturer
- \(c_{mf} \) :
-
unit freight cost from remanufacturer to retailer
- S(q):
-
expected sales, considering demand is D, \(S(q)=q-\int \limits _0^q {F(y)dy} \)
- l :
-
leftover value per remanufactured product after selling season
- s :
-
shortage cost per remanufactured product when demand is unsatisfied
- \(k_s \) :
-
government subsidies per remanufactured product
Revenue-sharing contact parameters:
- \(\{w_r ,\phi \}\) :
-
a pair of parameters in revenue-sharing contact
- \(w_r \) :
-
the parameter in revenue-sharing contract that represents the wholesale-price offered by remanufacturer to retailer for each used product collected
- \(\phi \) :
-
the parameter in revenue-sharing contract that represents a percentage of the revenue for remanufactured products offered by remanufacturer to retailer
- T :
-
transfer payment between retailer and remanufacturer, and \(T=T(w_r ,\phi )\)
- \(w_r^{\max } \) :
-
the maximum value of \(w_r \) under the constraint that the RSC achieves coordination
- \(\phi ^{\max }\) :
-
the maximum value of \(\phi \) under the constraint that the RSC achieves coordination
Appendix 2: Proof of theorems and observations
Proof of Theorem 1
(A) Take \(p_r^D\) as unknown variable in Eq. (9). (B) According to \(Q=a\cdot p_r \). (C) It is obviously. End of proof. \(\square \)
Proof of Theorem 2
Make the partial derivative with respect to \(p_r\) in profit function of remanufacturer. End of proof. \(\square \)
Proof of Observation 1
Compare Eqs. (7) and (19), it finds that \({p_r^C }/{p_r^D }>\frac{4(B-A)+a(P+s-l)\left( {E(\xi )} \right) ^{2}}{2(B-A)+a(P+s-l)\left( {E(\xi )} \right) ^{2}}>1.\) One gets \(p_r^C >p_r^D \). End of proof. \(\square \)
Proof of Theorem 3
(A) Take \(p_r^C\) as unknown variable in Eq. (20). (B) According to \(Q=a\cdot p_r \). End of proof. \(\square \)
Proof of Theorem 4
Similar to the proof of Theorem 2. End of proof. \(\square \)
Proof of Theorem 5
The deformation of Eq. (17) and (25) is below,
Since \(E\left( {\prod _m^{RS} } \right) =\lambda \cdot E\left( {\prod _{SC}^C } \right) \), one gets two equations below,
And
Simultaneous two equations above, one gets the equations below with three variables \(\lambda \), \(w_r \) and \(\phi \),
Then, delete \(\lambda \) in those two equations above, one gets
Besides, based on the assumption, \(E\left( {\prod _m^{RS} } \right) =\lambda \cdot E\left( {\prod _{SC}^C } \right) \), so \(E\left( {\prod _{SC}^{RS} } \right) =E\left( {\prod _{SC}^C } \right) \) (the objective function is exactly the same: \(E\left( {\prod _{SC}^C } \right) \) and \(\lambda \cdot E\left( {\prod _{SC}^C } \right) )\). End of proof. \(\square \)
Proof of Observation 2
\(P<\Lambda \)
End of proof. \(\square \)
Proof of Observation 3
In Theorem 5, let \(\phi =0\), then the maximum value of \(w_r \) can be got. And it is easy to see that if \(w_r^{\max } >0\), there is no positive terms in remanufacturer’s profit function. End of proof. \(\square \)
Proof of Observation 4
In Theorem 5, let \(w_r =0\), the proof is similar to Observation 3. End of proof. \(\square \)
Proof of Theorem 6
In decentralized case, let’s assume that \(w=w_r \), \(\Pi _m^d \ge 0\) and \(\Pi _r^d \ge 0\). It is known that \(\Pi _{SC}^d =\Pi _m^d +\Pi _r^d \) and the RSC couldn’t get optimal profit in decentralized case.
Hence in this respect, after coordination process, the RSC profit in revenue-sharing contract surely become larger than the wholesale-price contract, \(\Pi _{SC}^{RS} \ge \Pi _{SC}^d \). In other words, \(\Pi _m^{RS} +\Pi _r^{RS} \ge \Pi _m^d +\Pi _r^d \). Considering the set of contract parameters lies on a continuous straight line, which means the profit can allocate arbitrarily, consequently, there exists at least one point on the line \(w_r =w_r \left( \phi \right) ,0\le \phi \le 1\), that meets one of those three cases below,
End of proof. \(\square \)
Proof of Theorem 7
Similar to Theorem 5. End of proof. \(\square \)
Proof of Theorem 8
According to Theorem 1 in decentralized case, add \(k_s \xi \) into the Equation (12), considering
so \(Q_{with\,subsidies} -Q_{without\,subsidies} =\frac{a\left( {B-A} \right) k_s \xi }{4(B-A)+a\cdot \xi ^{2}\left( {P+s-l} \right) }\).
\(E_{with\,subsidies} \left( {\prod _{SC}^D } \right) -E_{without\,subsidies} \left( {\prod _{SC}^D } \right) =k_s \xi \cdot \Delta Q=k_s \xi \cdot \frac{a\left( {B-A} \right) k_s \xi }{4(B-A)+a\cdot \xi ^{2}\left( {P+s-l} \right) }.\) End of proof. \(\square \)
Proof of Theorem 9
Similar to Theorem 8. End of proof. \(\square \)
Appendix 3: Introduction and MATLAB code of the Newton–Raphson method
Let’s assume the problem is finding the root of function \(f(x)=0,x\in \left[ {A,B} \right] \), and f(x) is a continuously differentiable function on interval \(\left( {A,B} \right) \).
Let’s assume the current guess is \(x_n \) and this is incorrect by an amount h. Consequently \(x_n +h\) is the required value. It remains for us to determine h now or find an approximation to \(x_n +h\) at least. The Taylor expansion for the function f(x) at point \(x+h\) is given by
which means the value of the function f(x) at \(x_n +h\) is nearly equal to the value of the function f(x) at \(x_n \) plus the gradient at \(x_n \) times the distance between \(x_n +h\) and \(x_n \). And the error is a second order of h. Loosely this error equals to something the same size as \(h^{2}\). In fact, \(O(h^{2})\) also means differentiated with respect to x the argument of the function. Considering \(x_n +h\) is the required value, \(f(x_n +h)=0\). After discarding the higher-order terms \(O(h^{2})\) one finds that
This allows us to construct the iterative scheme
In these Iterative derivations the function is taken to be approximated by a “straight line” in order to determine the next point. And the “straight line” is the tangent on the point \(\left( {x_n ,f\left( {x_n } \right) } \right) \).
The MATLAB Code of Newton–Raphson method is provided:
%
% Newton_Raphson_method.m
%
x = input(“Starting from one guess point:”)
tolerance = 1e-6;
iterations = 0;
while \((iterations<100)\) & \((abs(func(x))>tolerance)\)
x = x-func(x)./func_prime(x);
iterations = iterations + 1;
end
if iterations==100
disp(’No root is found’)
else
disp([’The Root of function = ’ num2str(x,10) ’is found in ’ int2str(iterations)’ iterations.’])
end
%below is the function func_prime(x)
%
%func_prime.m
%
function [derivative] = func_prime(x)
%” derivative” will change based on your function, for example \(f(x) = e^{x}+7x^{2}-17,\) then
derivative=e. \(\hat{\,}\) x+14.* x;
Rights and permissions
About this article
Cite this article
Zhao, S., Zhu, Q. Remanufacturing supply chain coordination under the stochastic remanufacturability rate and the random demand. Ann Oper Res 257, 661–695 (2017). https://doi.org/10.1007/s10479-015-2021-3
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10479-015-2021-3