Abstract
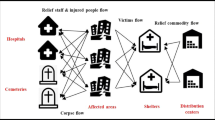
This paper introduces the element of beneficiaries’ choice into a location-routing problem for disaster relief logistics suited for decision support systems. Decision makers in humanitarian logistics face the challenge where to establish distribution centers (DCs) for relief goods. For this purpose, two objectives are considered: the impact of the relief operations on the beneficiaries and the efficient use of monetary resources. The proposed multi-objective location-routing model minimizes unserved demand as well as cost for opening DCs and for routing relief goods. It anticipates the choice of beneficiaries to which DC to go (if at all), based on a model adopted from the literature on competitive location analysis. A mathematical programming formulation is presented. For small instances, the Pareto front can be determined exactly using an epsilon constraint method. For solving also realistic instances, an evolutionary algorithm has been implemented and evaluated. The algorithms are tested on real-world instances from Mozambique. The results show that when designing a distribution network, improvements can be achieved by taking the predicted behavior of beneficiaries into account.





Similar content being viewed by others
Notes
Presenting more than one distance would increase the precision of the estimate, but it would require a statistical parameter estimation technique. We omit here the details.
References
Aboolian, R., Berman, O., & Krass, D. (2007). Competitive facility location and design problem. European Journal of Operational Research, 182(1), 40–62.
Berman, O., & Krass, D. (2002). Locating multiple competitive facilities: Spatial interaction models with variable expenditures. Annals of Operations Research, 111(1–4), 197–225.
Clarke, G., & Wright, J. W. (1964). Scheduling of vehicles from a central depot to a number of delivery points. Operations Research, 12(4), 568–581.
Current, J., & Schilling, D. (1989). The covering salesman problem. Transportation Science, 23, 208–213.
Deb, K., Pratap, A., Agarwal, S., & Meyarivan, T. (2002). A fast and elitist multiobjective genetic algorithm: “NSGA-II”. IEEE Transactions on Evolutionary Computation, 6(2), 182–197.
Doerner, K., Focke, A., & Gutjahr, W. J. (2007). Multicriteria tour planning for mobile healthcare facilities in a developing country. European Journal of Operational Research, 179(3), 1078–1096.
Drezner, T., & Drezner, Z. (2012). Modelling lost demand in competitive facility location. Journal of the Operational Research Society, 63(2), 201–206.
Drezner, T., Drezner, Z., & Kalczynski, P. (2011). A cover-based competitive location model. Journal of the Operational Research Society, 62(1), 100–113.
Eiselt, H. A., & Laporte, G. (1998). Demand allocation functions. Location Science, 6(1), 175–187.
Erdoğan, G., Cordeau, J. F., & Laporte, G. (2010). The attractive traveling salesman problem. European Journal of Operational Research, 203(1), 59–69.
Gendreau, M., Laporte, G., & Semet, F. (1997). The covering tour problem. Operations Research, 45, 568–576.
Hachicha, M., John Hodgson, M., Laporte, G., & Semet, F. (2000). Heuristics for the multi-vehicle covering tour problem. Computers & Operations Research, 27(1), 29–42.
Harris, F. W. (1990). How many parts to make at once. Operations Research, 38(6), 947–950.
Hotelling, H. (1929). Stability in competition. The Economic Journal, 39(153), 41–57.
Huff, D. L. (1966). A programmed solution for approximating an optimum retail location. Land Economics, 42(3), 293–303.
Jozefowiez, N., Semet, F., & Talbi, E. G. (2007). The bi-objective covering tour problem. Computers & operations research, 34(7), 1929–1942.
Laumanns, M., Thiele, L., & Zitzler, E. (2006). An efficient, adaptive parameter variation scheme for metaheuristics based on the epsilon-constraint method. European Journal of Operational Research, 169(3), 932–942.
Miller, C. E., Tucker, A. W., & Zemlin, R. A. (1960). Integer programming formulation of traveling salesman problems. Journal of the ACM, 7(4), 326–329.
Naji-Azimi, Z., Renaud, J., Ruiz, A., & Salari, M. (2012). A covering tour approach to the location of satellite distribution centers to supply humanitarian aid. European Journal of Operational Research, 222(3), 596–605.
Nolz, P. C., Doerner, K. F., & Hartl, R. F. (2010). Water distribution in disaster relief. International Journal of Physical Distribution & Logistics Management, 40, 693–708.
Tomasini, R., & van Wassenhove, L. (2009). Humanitarian Logistics. Basingstoke: Palgrave Macmillan.
Tricoire, F., Graf, A., & Gutjahr, W. J. (2012). The bi-objective stochastic covering tour problem. Computers & Operations Research, 39, 1582–1592.
van Wassenhove, L. (2006). Blackett memorial lecture. humanitarian aid logistics: Supply chain management in high gear. Journal of the Operational Research Society, 57, 475–489.
Zitzler, E., & Thiele, L. (1999). Multiobjective evolutionary algorithms: A comparative case study and the strength pareto approach. IEEE Transactions on Evolutionary Computation, 4, 257–271.
Zitzler, E., Thiele, L., Laumanns, M., Fonseca, C. M., & Da Fonseca, V. G. (2003). Performance assessment of multiobjective optimizers: An analysis and review. IEEE Transactions on Evolutionary Computation, 7(2), 117–132.
Acknowledgments
The authors thank Mario Ruthmair for providing his expertise in mathematical modeling.
Author information
Authors and Affiliations
Corresponding author
Appendix: Capacity calculation
Appendix: Capacity calculation
The DC capacity calculation is explained here in more detail:
A first idea (see Equation (50)) for calculating appropriate capacities of DCs in a beneficiaries choice model was to sum up the number of inhabitants of the PCs within the sphere of influence of the DC and dividing it by the average number of DCs available to the PCs considered this way. Here , \(M_{i_k}\) is the set of PCs k within the sphere of influence of DC i, \(m_i\) is the number of PCs within sphere of influence from DC i and \(n_k\) is the number of DCs within sphere of influence of PC k. This resulted in very low levels of capacity, forcing the opening of the majority of DCs to supply the population.
Therefore, a concept following the logic of the Economic Order Quantity (EOQ) of Harris (1990) is employed. For this purpose, the cost to deliver to a DC has been approximated by considering full truckloads in \(c_{FTL_i}=2 \cdot d_{0i}\). If the fixed cost for the DC is now divided by the approximated cost to deliver goods, one can see the ratio of those cost types \(r_{EOQ}\) (see Equation (51)). A high ratio would signal high opening cost, and favoring less opened DC with higher capacities from a cost perspective, while lower ratios describe a situation in which the fixed opening cost is not so dominant, allowing for more DCs with lower capacities.
The \(r_{EOQ}\) is used to adjust the capacities for this cost ratios to increase the capacities if it is advisable from a cost perspective while the focus on the unserved remains intact due to considering only everything within the sphere of influence.
Constraint (53) makes sure that at least all demand can be fulfilled if every DC is opened, and that the capacities of the DCs are not higher than necessary to supply all PCs within the sphere of influence.
Rights and permissions
About this article
Cite this article
Burkart, C., Nolz, P.C. & Gutjahr, W.J. Modelling beneficiaries’ choice in disaster relief logistics. Ann Oper Res 256, 41–61 (2017). https://doi.org/10.1007/s10479-015-2097-9
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10479-015-2097-9