Abstract
Owing to the importance of internal structure of decision making units (DMUs) and data uncertainties in real situations, the present paper focuses on multi-component data envelopment analysis (MC-DEA) approach with imprecise data. The undesirable outputs and shared resources are also incorporated in the production process of multi-component DMUs to validate real problems. The interval efficiencies of DMUs and their components in MC-DEA are often challenging with imprecise data. In many practical situations, different set of weights may be resulted into valid efficiency intervals for DMUs but invalid interval efficiencies for their components. Therefore, the present study proposes a new common set of weights methodology, based on interval arithmetic and unified production frontier, to determine unique weights for measuring these interval efficiencies. It is a two-level mathematical programming approach that preserves linearity of DEA and exhibits stronger discrimination power among the DMUs as compared to some existing approaches. Theoretically, the aggregate efficiency interval of each DMU lies between the components’ interval efficiencies. Further, the proposed approach is also applied to banks in India for proving its acceptability in practical applications. The performance of each bank is investigated in terms of two components: general business and bancassurance business for the years 2011–2013. The present study emphasized expanding pattern of bancassurance business in current market scenario with more percentage increase as contrasted to general business.




Similar content being viewed by others
References
Amin, G. R., & Toloo, M. (2007). Finding the most efficient DMUs in DEA: An improved integrated model. Computers & Industrial Engineering, 52, 71–77.
Amirteimoori, A., & Kordrostami, S. (2005). Multi-component efficiency measurement with imprecise data. Applied Mathatics and Computation, 162, 1265–1277.
Ashrafi, & Jaafar, A. B. (2011). Efficiency measurement of series and parallel production systems with interval data by data envelopment analysis. Australian Journal of Basic and Applied Sciences, 5(11), 1435–1443.
Azar, A., Mahmoudabadi, M. Z., & Emrouznejad, A. (2016). A new fuzzy additive model for determining the common set of weights in data envelopment analysis. Journal of Intelligent & Fuzzy Systems, 30, 61–69.
Azizi, H. (2014). A note on ”Supplier selection by the new AR-IDEA model”. International Journal of Advanced Manufacturing Technology, 71, 711–716.
Bi, G., Ding, J., Luo, Y., & Liang, L. (2011). Resource allocation and target setting for parallel production system based on DEA. Applied Mathematical Modelling, 35, 4270–4280.
Castelli, L., Pesenti, R., & Ukovich, W. (2010). A classification of DEA models when the internal structure of the decision making units is considered. Annals of Operations Research, 173, 207–235.
Charnes, A., Cooper, W. W., & Rhodes, E. (1978). Measuring the efficiency of decision making units. European Journal of Operational Research, 2, 429–444.
Chen, Y., Du, J., Sherman, H. D., & Zhu, J. (2010). DEA model with shared resources and efficiency decomposition. European Journal of Operational Research, 207, 339–349.
Cook, W. D., Hababou, M., & Tuenter, H. J. H. (2000). Multicomponent efficiency measurement and shared inputs in DEA: An application to sales and service performance in bank branches. Journal of Productivity Analysis, 14(3), 209–224.
Cook, W. D., & Roll, Y. (1993). Partial efficiencies in data envelopment analysis. Socio-Economic Planning Sciences, 37(3), 171–179.
Cook, W. D., Roll, Y., & Kazakov, A. (1990). A DEA model for measuring the relative efficiency of highway maintenance patrols. INFOR, 28(2), 113–124.
Cook, W. D., Zhu, J., Bi, G. B., & Yang, F. (2010). Network DEA: Additive efficiency decomposition. European Journal of Operational Research, 207, 1122–1129.
Cooper, W. W., Park, K. S., & Yu, G. (1999). IDEA and AR-IDEA: Models for dealing with imprecise data in DEA. Management Science, 45, 597–607.
Cooper, W. W., Seiford, L. M., & Tone, K. (2007). Data envelopment analysis: A comprehensive text with models, applications, references and DEA-solver software (2nd ed.). New York: Springer.
Emrouznejad, A., & Tavana, M. (2014). Performance measurement with fuzzy data envelopment analysis. Berlin: Springer.
Emrouznejad, A. (2014). Advances in data envelopment analysis. Annals of Operations Reseach, 214(1), 1–4.
Emrouznejad, A., & Cabanda, E. (2015). Introduction to data envelopment analysis and its applications. In A. L. Osman, A. L. Anouze & A. Emrouznejad (Eds.), Handbook of research on strategic performance management and measurement using data envelopment analysis, (pp. 235–255). IGI Global.
Eslami, G. R., Mehralizadeh, M., & Jahanshahloo, G. R. (2009). Efficiency measurement of multi-component decision making units using data envelopment analysis. Applied Mathematical Sciences, 3(52), 2575–2594.
Färe, R., Grabowski, R., Grosskopf, S., & Kraft, S. (1997). Efficiency of a fixed but allocatable input: A non-parametric approach. Economics Letters, 56, 187–193.
Färe, R., & Grosskopf, S. (1996). Productivity and intermediate products: A frontier approach. Economics Letters, 50(1), 65–70.
Hosseinzadeh Lotfi, F., & Vaez-Ghasemi, M. (2013). Multi-component efficiency with shared resources in commercial banks. International Journal of Applied Operational Research, 3(4), 93–104.
Imanirad, R., Cook, W. D., & Zhu, J. (2013). Partial input to output impacts in DEA: Production considerations and resource sharing among business subunits. Naval Reserach Logistics, 60(3), 190–207.
Jahanshahloo, G. R., Amirteimoori, A. R., & Kordrostami, S. (2004a). Multi-component performance, progress and regress measurement and shared inputs and outputs in DEA for panel data: An application in commercial bank branches. Applied Mathatics and Computation, 151, 1–16.
Jahanshahloo, G. R., Amirteimoori, A. R., & Kordrostami, S. (2004b). Measuring the multi-component efficiency with shared inputs and outputs in data envelopment analysis. Applied Mathatics and Computation, 155, 283–293.
Jahanshahloo, G. R., Memariani, A., Hosseinzadeh Lotfi, F., & Rezaei, H. Z. (2005). A note on some DEA models and finding efficiency and complete ranking using common set of weights. Applied Mathematics and Computation, 166, 265–281.
Jelodar, M. F., Shoja, N., Sanei, M., & Abri, A. G. (2009). Efficiency measurement of multiple components units in data envelopment analysis using common set of weights. International Journal of Industrial Mathematics, 1(2), 183–195.
Kao, C. (2009a). Efficiency decomposition in network data envelopment analysis: A relational model. European Journal of Operational Research, 192, 949–962.
Kao, C. (2009b). Efficiency measurement for parallel production systems. European Journal of Operational Research, 196, 1107–1112.
Kao, C. (2012). Efficiency decomposition for parallel production systems. Journal of the Operational Research Society, 63, 64–71.
Kao, C. (2014a). Efficiency decomposition for general multi-stage systems in data envelopment analysis. European Journal of Operational Research, 232, 117–124.
Kao, C. (2014b). Network data envelopment analysis: A review. European Journal of Operational Research, 239, 1–16.
Khalili-Damghani, K., Tavana, M., & Haji-Saami, E. (2015). A data envelopment analysis model with interval data and undesirable output for combined cycle power plant performance assessment. Expert Systems with Applications, 42, 760–773.
Kordrostami, S., & Amirteimoori, A. (2005). Un-desirable factors in multi-component performance measurement. Applied Mathematics and Computation, 171, 721–729.
Korhonen, P. J., & Luptacik, M. (2004). Eco-efficiency analysis of power plants: An extension of data envelopment analysis. European Journal of Operational Research, 154, 437–446.
Lewis, H. F., & Sexton, T. R. (2004). Network DEA: Efficiency analysis of organizations with complex internal structure. Computers & Operations Research, 31, 1365–1410.
Liang, L., Li, Y., & Li, S. (2009). Increasing the discriminatory power of DEA in the presence of the undesirable outputs and large dimensionality of data sets with PCA. Expert Systems with Applications, 36, 5895–5899.
Liu, W. B., Meng, W., Li, X. X., & Zhang, D. Q. (2010). DEA models with undesirable inputs and outputs. Annals of Operations Research, 173(1), 177–194.
Liu, F. H. F., & Peng, H. H. (2008). Ranking of units on the DEA frontier with common weights. Computers & Operations Research, 35, 1624–1637.
Noora, A. A., Hosseinzadeh Lotfi, F., & Payan, A. (2011). Measuring the relative efficiency in multi-component decision making units and its application to bank branches. Journal of Mathematical Extension, 5(2), 101–119.
Omrani, H. (2013). Common weights data envelopment analysis with uncertain data: A robust optimization approach. Computers & Industrial Engineering, 66(4), 1163–1170.
Pourmahmoud, J., & Zeynali, Z. (2016). A nonlinear model for common weights set identification in network data envelopment analysis. International Journal of Industrial Mathematics, 8(1), 87–98.
Puri, J., & Yadav, S. P. (2013a). Performance evaluation of public and private sector banks in India using DEA. International Journal of Operational Research, 18(1), 91–121.
Puri, J., & Yadav, S. P. (2013b). A concept of fuzzy input mix-efficiency in fuzzy DEA and its application in banking sector. Expert Systems with Applications, 40, 1437–1450.
Puri, J., & Yadav, S. P. (2014). A fuzzy DEA model with undesirable fuzzy outputs and its application to the banking sector in India. Expert Systems with Applications, 41, 6419–6432.
Ramli, N. A., & Munisamy, S. (2013). Modeling undesirable factors in efficiency measurement using data envelopment analysis: A review. Journal of Sustainability Science and Management, 8(1), 126–135.
Ramón, N., Ruiz, J. L., & Sirvent, I. (2012). Common sets of weights as summaries of DEA profiles of weights: With an application to the ranking of professional tennis players. Expert Systems with Applications, 39, 4882–4889.
Rezaie, V., Ahmad, T., Awang, S. R., Khanmohammadi, M., & Maan, N. (2014). Ranking DMUs by calculating the interval efficiency with a common set of weights in DEA. Journal of Applied Mathematics, Article ID 346763, 9.
Roll, Y., Cook, W. D., & Golany, B. (1991). Controlling factor weights in data envelopment analysis. IIE Transactions, 23(1), 2–9.
RBI. (2012). Reserve Bank of India: Statistical tables relating to banks in India, 2011–2012. Available from http://rbidocs.rbi.org.in/rdocs/Publications/PDFs/00STB071112FLS.pdf.
RBI. (2013a). Reserve Bank of India: Statistical tables relating to Banks in India, 2012–2013. Available from http://rbidocs.rbi.org.in/rdocs/Publications/PDFs/0STR191113FL.pdf.
RBI. (2013b). Reserve Bank of India: Master circular—prudential norms on income recognition, asset classification and provisioning pertaining to advances, 2013. Available from http://rbidocs.rbi.org.in/rdocs/notification/PDFs/62MCIRAC290613.pdf.
Scheel, H. (2001). Undesiarable outputs in efficiency valuations. European Journal of Operational Research, 132(2), 400–410.
Seiford, L., & Zhu, J. (2002). Modeling undesirable factors in efficiency evaluation. European Journal of Operational Research, 142(1), 16–20.
Toloo, M., Emrouznejad, A., & Moreno, P. (2015). A linear relational DEA model to evaluate two-stage processes with shared inputs. Computational and Applied Mathematics, 34, 1–17.
Tyagi, P., Yadav, S. P., & Singh, S. P. (2009). Relative performance of academic departments using DEA with senstivity analysis. Evaluation and Program Planning, 32(2), 168–177.
Wang, Y. M., Greatbanks, R., & Yang, J. B. (2005). Interval efficiency assessment using data envelopment analysis. Fuzzy Sets and Systems, 153, 347–370.
Wu, J., Zhu, Q., Chu, J., & Liang, L. (2015). Two-stage network structures with undesirable intermediate outputs reused: A DEA based approach. Computational Economics, 46, 455–477.
Yang, Y., Ma, B., & Koike, M. (2000). Efficiency-measuring DEA model for production system with k independent subsystems. Journal of the Operations Research Society of Japan, 43, 343–354.
Zhou, G., Chung, W., & Zhang, Y. (2014). Measuring energy efficiency performance of China’s transport sector: A data envelopment analysis approach. Expert Systems with Applications, 41, 709–722.
Zhu, J. (2003). Imprecise data envelopment analysis (IDEA): A review and improvemet with an application. European Journal of Operational Research, 144, 513–529.
Acknowledgements
The authors are thankful to the editor and anonymous reviewers for their constructive comments and suggestions that helped us in improving the paper significantly.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A
See Table 10.
Appendix B: Proofs of theorems
1.1 Proof of Theorem 1
Proof
The aggregate efficiency \({E}_{k}^{ (a)} \) is given by
Let \(\lambda _i ={\left( {{V}_{k}^{(i)} {X}_{k}^{(i)} +{V}_{k}^{S(i)} \left( \alpha _{ik} {X}_{k}^S \right) } \right) }/H, i=1,2,3,\ldots ,d.\) Also \(\lambda _i \ge 0 \,\forall i\).\(\square \)
Hence, \({E}_{k}^{ (a)} =\sum \limits _{i=1}^d {\lambda _i {E}_{k}^{ (i)} } \) for each \(\lambda _i \ge 0\) and \(\sum \limits _{i=1}^d {\lambda _i } =1\). This completes the proof.
1.2 Proof of Theorem 3
Proof
Let \(H=\sum \limits _{i=1}^d {\sum \limits _{l=1}^{{I}_{i} } {v_{lk}^{(i)} x_{lk}^{{(i)} {U}}} } +\sum \limits _{i=1}^d {\sum \limits _{t=1}^{I^{S}} {v_{tk}^{S(i)} (\alpha _{ik}^t x_{tk}^{S {U}})} } \). Then,
where \(\lambda _i ={\left( {\sum \limits _{l=1}^{{I}_{i} } {v_{lk}^{(i)} x_{lk}^{{(i)} {U}}} +\sum \limits _{t=1}^{I^{S}} {v_{tk}^{S(i)} (\alpha _{ik}^t x_{tk}^{S {U}})} } \right) }\Big /H, i=1,2,3,\ldots ,d.\) Also \(\lambda _i \ge 0 \,\forall i\).\(\square \)
Hence, \({E}_{k}^{ (a)L} =\sum \limits _{i=1}^d {\lambda _i {E}_{k}^{ (i)L} } \) for each \(\lambda _i \ge 0\) and \(\sum \limits _{i=1}^d {\lambda _i } =1.\) This completes the proof.
1.3 Proof of Theorem 6
Proof
Assume that \({E}_{k}^{ (i)U^*} = 1, \forall i=1,2,\ldots ,d.\) By Theorem 4, \({E}_{k}^{ (a)U^*} =\sum \limits _{i=1}^d {\lambda _i {E}_{k}^{ (i)U^*} } \) and since \(\sum \limits _{i=1}^d {\lambda _i } =1\) for \(\lambda _i \in [0,1] \,\forall i\), it follows that each \({E}_{k}^{ (a)U^*} =1\).\(\square \)
Now assume that \({E}_{k}^{ (a)U^*} =1.\) If any \({E}_{k}^{ (i)U^*} <1 \,\forall i\in \{1,2,\ldots ,d\}\) then, \({E}_{k}^{ (a)U^*} =\sum \limits _{i=1}^d {\lambda _i {E}_{k}^{ (i)U^*} } <1\) which is a contradiction. Hence, \({E}_{k}^{ (a)U^*} = 1\Leftrightarrow {E}_{k}^{ (i)U^*} =1, \forall i=1,2,\ldots ,d\).
1.4 Proof of Theorem 7
Proof
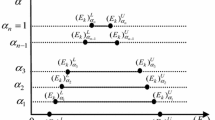
Let \((u_{1k}^{(i)^*} ,u_{2k}^{(i)^*} ,\ldots ,u_{rk}^{(i)^*} ;v_{1k}^{(i)^*} ,v_{2k}^{(i)^*} ,\ldots ,v_{lk}^{(i)^*} ), \forall r,l\) be the optimal solution to Model-7 when the production process of multi-component \(\hbox {DMU}_{k}\) is of the form of Fig. 2. Then, the following equalities and inequalities hold:
For \(\hbox {DMU}_{k}\), we have
For DMU\(_{j} \quad (j=1,2,\ldots ,n; j\ne k),\) we get
Equations (9)–(13) implies that \((u_{1k}^{(i)^*} ,u_{2k}^{(i)^*} ,\ldots ,u_{rk}^{(i)^*} ;v_{1k}^{(i)^*} ,v_{2k}^{(i)^*} ,\ldots ,v_{lk}^{(i)^*} ), \forall r,l\) is a feasible solution to Model-4b. Thus, we have the following inequality relation:
Similarly, if \((u_{1k}^{(i)^*} ,u_{2k}^{(i)^*} ,\ldots ,u_{rk}^{(i)^*} ;v_{1k}^{(i)^*} ,v_{2k}^{(i)^*} ,\ldots ,v_{lk}^{(i)^*} ), \forall r,l\) be the optimal solution to Model-8 when the production process of multi-component \(\hbox {DMU}_{k}\) is of the form of Fig. 2.
Therefore, for \(\hbox {DMU}_{k}\), we have
For DMU\(_{j} \quad (j=1,2,\ldots ,n; j\ne k),\) we have
Equations (14)–(18) implies that \((u_{1k}^{(i)^*} ,u_{2k}^{(i)^*} ,\ldots ,u_{rk}^{(i)^*} ;v_{1k}^{(i)^*} ,v_{2k}^{(i)^*} ,\ldots ,v_{lk}^{(i)^*} ), \forall r,l\) is a feasible solution to Model-4a. Thus, we have the following inequality relation:
This completes the proof.\(\square \)
Appendix C: Proofs of propositions
1.1 Proof of Proposition 1
Proof
By Theorem 3, we have \({E}_{k}^{ (a)L^*} =\sum \limits _{i=1}^d {\lambda _i {E}_{k}^{ (i)L^*} } \) for each \(\lambda _i \ge 0\) and \(\sum \limits _{i=1}^d {\lambda _i } =1.\)
Equations (19) and (20) implies that \({M}_{k} \le {E}_{k}^{(a)L^*} \le {N}_{k}\).\(\square \)
1.2 Proof of Proposition 2
Proof
By Theorem 4, we have \({E}_{k}^{ (a)U^*} =\sum \limits _{i=1}^d {\lambda _i {E}_{k}^{ (i)U^*} } \) for each \(\lambda _i \ge 0\) and \(\sum \limits _{i=1}^d {\lambda _i } =1\).
Equations (21) and (22) implies that \({P}_{k} \le {E}_{k}^{(a)U^*} \le {Q}_{k} .\) \(\square \)
Appendix D: Minimax regret-based approach (MRA) for ranking interval efficiencies in MC-DEA
In interval efficiency assessment problem, the final efficiency score of every DMU is characterized by an interval. Wang et al. (2005) proposed an interesting approach, named as minimax regret-based approach (MRA), to compare and rank the DMUs that possess interval efficiencies. The main advantage of this approach is that it can be used to compare and rank the intervals even if they are equi-centered but different in widths. To rank efficiency intervals, Wang et al. (2005) defined maximum regret as follows:
Let \({A}_{k} =[{a}_{k}^{L} ,{a}_{k}^{U} ] = \left\langle {m({A}_{k} ), w({A}_{k} )} \right\rangle (k=1,2,\ldots ,n)\) be the efficiency interval of the kth DMU where \(m({A}_{k} )={({a}_{k}^{U} +{a}_{k}^{L} )}/2\) is the midpoint of \({A}_{k} \) and \(w({A}_{k} )={({a}_{k}^{U} -{a}_{k}^{L} )}/2\) is the width of \({A}_{k} \). The maximum loss of efficiency (or maximum regret) of each \({A}_{k}\, (k=1,2,\ldots ,n)\) is defined as
It is obvious that the efficiency interval with the smallest maximum loss of efficiency is the best (most desirable) efficiency interval. In order to generate a ranking for a set of efficiency intervals using the above discussed maximum loss of efficiency, Wang et al. (2005) suggested minimax regret-based approach which is an eliminating process. In this ranking approach, firstly, evaluate the maximum loss of efficiency (regret) of all n efficiency intervals and eliminate a most desirable efficiency interval (say \(A_{{k}_{1} } , 1\le {k}_{1} \le n)\) that has the smallest maximum loss of regret. Further, recalculate the maximum loss of regret of each efficiency interval and eliminate a most desirable efficiency interval (say (say \(A_{{k}_{2} } , 1\le {k}_{2} \le n, {k}_{2} \ne {k}_{1} )\) from the remaining \((n-1)\) efficiency intervals. Repeat the above eliminating process until only one efficiency interval \(A_{k_n } \)is left. Then, the final ranking is given by \(A_{{k}_{1} } \succ A_{{k}_{2} } \succ \cdots \succ A_{k_n }\), where the symbol ‘\(\succ \)’ means ‘is superior to’. This ranking approach is referred to as MRA.
Rights and permissions
About this article
Cite this article
Puri, J., Yadav, S.P. & Garg, H. A new multi-component DEA approach using common set of weights methodology and imprecise data: an application to public sector banks in India with undesirable and shared resources. Ann Oper Res 259, 351–388 (2017). https://doi.org/10.1007/s10479-017-2540-1
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10479-017-2540-1