Skip to main content

Advertisement

Springer Nature Link
Log in

Equilibrium threshold joining strategies in partially observable batch service queueing systems

  • Queueing Theory and Network Applications
  • Published:
Annals of Operations Research Aims and scope Submit manuscript

Abstract

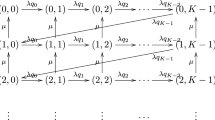
We study the strategic customer behavior in queueing systems with batch services under incomplete information. In particular, we assume that arriving customers have the opportunity to observe only the number of waiting batches upon arrival and, afterwards, they make their join/balk decisions. We prove that equilibrium strategies always exist within the legitimate class of threshold strategies, but they may not be unique. We also provide an algorithmic scheme for their computation. Moreover, we compare the strategic behavior under this information level with the corresponding behavior in the complete information case.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  • Adiri, I., & Yechiali, U. (1974). Optimal priority purchasing and pricing decisions in non-monopoly and monopoly queues. Operations Research, 22, 1051–1066.

    Article  Google Scholar 

  • Afimeimounga, H. (2011). User optimal policies for a stochastic transportation network. Ph.D. Thesis, University of Auckland.

  • Afimeimounga, H., Solomon, W., & Ziedins, I. (2005). The Downs–Thomson paradox: Existence, uniqueness and stability of user equilibria. Queueing Systems, 49, 321–334.

    Article  Google Scholar 

  • Afimeimounga, H., Solomon, W., & Ziedins, I. (2010). User equilibria for a parallel queueing system with state dependent routing. Queueing Systems, 62, 169–193.

    Article  Google Scholar 

  • Boudali, O., & Economou, A. (2012). Optimal and equilibrium balking strategies in the single server Markovian queue with catastrophes. European Journal of Operational Research, 218, 708–715.

    Article  Google Scholar 

  • Boudali, O., & Economou, A. (2013). The effect of catastrophes on the strategic customer behavior in queueing systems. Naval Research Logistics, 60, 571–587.

    Article  Google Scholar 

  • Bountali, O., & Economou, A. (2017). Equilibrium joining strategies in batch service queueing systems. European Journal of Operational Research, 260, 1142–1151.

    Article  Google Scholar 

  • Burnetas, A., & Economou, A. (2007). Equilibrium customer strategies in a single server Markovian queue with setup times. Queueing Systems, 56, 213–228.

    Article  Google Scholar 

  • Calvert, B. (1997). The Downs–Thomson effect in a Markov process. Probability in the Engineering and Informational Sciences, 11, 327–340.

    Article  Google Scholar 

  • Chen, Y., Holmes, M., & Ziedins, I. (2012). Monotonicity properties of user equilibrium policies for parallel batch systems. Queueing Systems, 70, 81–103.

    Article  Google Scholar 

  • Economou, A., & Kanta, S. (2008a). Optimal balking strategies and pricing for the single server Markovian queue with compartmented waiting space. Queueing Systems, 59, 237–269.

    Article  Google Scholar 

  • Economou, A., & Kanta, S. (2008b). Equilibrium balking strategies in the observable single-server queue with breakdowns and repairs. Operations Research Letters, 36, 696–699.

    Article  Google Scholar 

  • Economou, A., & Manou, A. (2013). Equilibrium balking strategies for a clearing queueing system in alternating environment. Annals of Operations Research, 208, 489–514.

    Article  Google Scholar 

  • Edelson, N. M., & Hildebrand, K. (1975). Congestion tolls for Poisson queueing processes. Econometrica, 43, 81–92.

    Article  Google Scholar 

  • Guo, P., & Zipkin, P. (2007). Analysis and comparison of queues with different levels of delay information. Management Science, 53, 962–970.

    Article  Google Scholar 

  • Guo, P., & Zipkin, P. (2009). The effects of the availability of waiting-time information on a balking queue. European Journal of Operational Research, 198, 199–209.

    Article  Google Scholar 

  • Hassin, R. (2016). Rational queueing. Boca Raton: CRC Press, Taylor and Francis Group.

    Book  Google Scholar 

  • Hassin, R., & Haviv, M. (1997). Equilibrium thresholds strategies: The case of queues with priorities. Operations Research, 45, 966–973.

    Article  Google Scholar 

  • Hassin, R., & Haviv, M. (2003). To queue or not to queue: Equilibrium behavior in queueing systems. Boston: Kluwer Academic Publishers.

    Book  Google Scholar 

  • Latouche, G., & Ramaswami, V. (1999). Introduction to matrix analytic methods in stochastic modeling. Philadelphia: SIAM-ASA.

    Book  Google Scholar 

  • Manou, A., Economou, A., & Karaesmen, F. (2014). Strategic customers in a transportation station: When is it optimal to wait? Operations Research, 62, 910–925.

    Article  Google Scholar 

  • Naor, P. (1969). The regulation of queue size by levying tolls. Econometrica, 37, 15–24.

    Article  Google Scholar 

  • Pai, H.-M., & Cheng, W.-H. (2012). User optimal policy for a parallel queueing system with state dependent routing under the \(M/M^{(N)}/K\) batch service. Preprint available at https://www.ntpu.edu.tw/stat/chinese/journal/journal-1-14-3.pdf.

  • Stidham, S, Jr. (2009). Optimal design of queueing systems. Boca Raton: CRC Press, Taylor and Francis Group.

    Book  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Engineering Management, Information, and Systems, Southern Methodist University, 3145 Dyer Street, P.O. Box 750123, Dallas, TX, 75275-0123, USA

    Olga Bountali

  2. Department of Mathematics, University of Athens, Panepistemiopolis, 15784, Athens, Greece

    Antonis Economou

Authors
  1. Olga Bountali
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Antonis Economou
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Antonis Economou.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Bountali, O., Economou, A. Equilibrium threshold joining strategies in partially observable batch service queueing systems. Ann Oper Res 277, 231–253 (2019). https://doi.org/10.1007/s10479-017-2630-0

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10479-017-2630-0

Keywords