Development of a single period inventory planning model for perishable product redistribution

Abstract

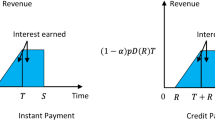
Considering that more than 100 million EU citizens face the risk of poverty or social exclusion, while at the same time 35% of perishable food in the EU is unnecessarily discarded at supermarkets, the redistribution of the perishable food surpluses could provide an economically feasible solution towards the confrontation of poverty and the minimization of food waste. Under this context, the purpose of this paper is to propose a novel quantitative decision-making tool that optimizes a retailer’s replenishment policy for perishable products while minimizing the amount of perishable items discarded after they approach their expiration dates, through the timely donation of a part of their net stocks.

Appendix 1

Our optimizations process initially involves the derivation of each one of the profit function components separately, as these are summarized below:

$$ \begin{aligned} E(BO_{T}) & = \sigma_{y} \cdot \int_{{Q - q_{0}}}^{\infty} {\varphi_{\varUpsilon} (z_{Q - x}) \cdot \varphi_{X} (x)\,dx} \,\, + \,\sigma_{y} \cdot \int_{{Q - q_{0}}}^{\infty} {\left({x - Q} \right) \cdot (1 - \varPhi_{\varUpsilon} (z_{Q - x})) \cdot \varphi_{X} (x)\,dx} \\ & \quad + \sigma_{y} \cdot \varphi_{\varUpsilon} (z_{{q_{0}}}) \cdot \varPhi_{X} (Q - q_{0}) - \sigma_{y} \cdot q_{0} \cdot (1 - \varPhi_{\varUpsilon} (z_{{q_{0}}}) \cdot \varPhi_{X} (Q - q_{0}) \\ \end{aligned} $$

$$ \begin{aligned} E(OH_{T}) & = \sigma_{y} \cdot \int_{{Q - q_{0}}}^{Q} {\left({Q - x} \right) \cdot \,\varPhi_{\varUpsilon} (z_{Q - x})\varphi_{X} (x)\,dx}\\&\quad - \int_{{Q - q_{0}}}^{Q} {\left({\mu_{y} - \sigma_{y} \cdot \varphi_{\varUpsilon} (z_{Q - x})} \right) \cdot \,} \varphi_{X} (x)\,dx + \sigma_{y} \cdot q_{0} \cdot \varPhi_{\varUpsilon} (z_{{q_{0}}}) \cdot \varPhi_{X} (Q - q_{0})\\ & \quad - \left({\mu_{y} - \sigma_{y} \cdot \varphi_{\varUpsilon} (z_{{q_{0}}})} \right) \cdot \varPhi_{X} (Q - q_{0}) \\ \end{aligned} $$

$$ \begin{aligned} E(Sales_{T}) & = \int_{{Q - q_{0}}}^{\infty} {Q \cdot \left({1 - \varPhi_{\varUpsilon} (z_{Q - x})} \right)\,\varphi_{X} (x)\,dx} + \sigma_{y} \cdot \int_{{Q - q_{0}}}^{Q} {x \cdot \varPhi_{\varUpsilon} (z_{Q - x}) \cdot \varphi_{X} (x)\,dx} \\ & \quad + \int_{{Q - q_{0}}}^{Q} {\left({\mu_{y} - \sigma_{y} \cdot \varphi_{\varUpsilon} (z_{Q - x})} \right) \cdot \varphi_{X} (x)\,dx\,\,}\\ & \quad + \int_{0}^{{Q - q_{0}}} {\sigma_{y} \cdot \left({x + q_{0}} \right) \cdot \left({1 - \varPhi_{\varUpsilon} (z_{{q_{0}}})} \right)\varphi_{X} (x)\,dx} \\ & \quad + \int_{0}^{{Q - q_{0}}} {\sigma_{y} \cdot x \cdot \varPhi_{\varUpsilon} (z_{{q_{0}}}) \cdot \varphi_{X} (x)\,dx} + \left({\mu_{y} - \sigma_{y} \cdot \varphi_{\varUpsilon} (z_{{q_{0}}})} \right) \cdot \varPhi_{X} (Q - q_{0}) \\ \end{aligned} $$

Since:

• $\frac{{\partial \varPhi_{\varUpsilon} (z_{{q_{0}}})}}{{\partial q_{0}}} = \varphi_{\varUpsilon} (z_{{q_{0}}}) \cdot \frac{{\partial \cdot z_{{q_{0}}}}}{{\partial q_{0}}}$

• $\frac{{\partial \varphi_{\varUpsilon} (z_{{q_{0}}})}}{{\partial q_{0}}} = - z_{{q_{0}}} \cdot \varphi_{\varUpsilon} (z_{{q_{0}}}) \cdot \frac{{\partial \cdot z_{{q_{0}}}}}{{\partial q_{0}}}$

• $\frac{{\partial (Q-{q_0})}}{{\partial q_{0}}} = -1$

and by differentiating, each function with respect to $q_{0}$, considering the following Leibnitz rule:

$$ \frac{\partial}{{\partial q_{0}}}\int_{{a\left({q_{0}} \right)}}^{{b\left({q_{0}} \right)}} {f(x,q_{0})\partial x} = \int_{{a\left({q_{0}} \right)}}^{{b\left({q_{0}} \right)}} {\frac{{\partial f(x,q_{0})}}{{\partial q_{0}}}\partial x} + f(b\left({q_{0}} \right),q_{0})\frac{{\partial b\left({q_{0}} \right)}}{{\partial q_{0}}} - f(a\left({q_{0}} \right),q_{0})\frac{{\partial a\left({q_{0}} \right)}}{{\partial q_{0}}} $$

we obtain:

$$ \begin{aligned} \frac{{\partial E(BO_{T})}}{{\partial q_{0}}} & = - \sigma_{y} \cdot \varphi_{\varUpsilon} (z_{{q_{0}}})\varphi_{X} (Q - q_{0}) \cdot \frac{{\partial (Q - q_{0})}}{{\partial q_{0}}}\, \\ & \quad- \sigma_{y} \cdot \left({- q_{0}} \right) \cdot \left({1 - \varPhi_{\varUpsilon} (z_{{q_{0}}})} \right)\varphi_{X} (Q - q_{0}) \cdot \frac{{\partial (Q - q_{0})}}{{\partial q_{0}}} \\ & \quad - \,\sigma_{y} \cdot z_{{q_{0}}} \cdot \varphi_{\varUpsilon} (z_{{q_{0}}}) \cdot \frac{{\partial (z_{{q_{0}}})}}{{\partial q_{0}}} \cdot \varPhi_{X} (Q - q_{0}) + \,\sigma_{y} \cdot \varphi_{\varUpsilon} (z_{{q_{0}}}) \cdot \varphi_{X} (Q - q_{0}) \\ & \quad \cdot \frac{{\partial (Q - q_{0})}}{{\partial q_{0}}}- \sigma_{y} \cdot \,\left({1 - \varPhi_{\varUpsilon} (z_{{q_{0}}})} \right)\varPhi_{X} (Q - q_{0}) + \sigma_{y} \cdot q_{0} \cdot \,\varphi_{\varUpsilon} (z_{{q_{0}}}) \cdot \frac{{\partial (z_{{q_{0}}})}}{{\partial q_{0}}} \\ & \quad\cdot \varPhi_{X} (Q - q_{0}) - \sigma_{y} \cdot q_{0} \cdot \,\left({1 - \varPhi_{\varUpsilon} (z_{{q_{0}}})} \right)\varphi_{X} (Q - q_{0}) \cdot \frac{{\partial (Q - q_{0})}}{{\partial q_{0}}} \\ & = \sigma_{y} \cdot \varphi_{\varUpsilon} (z_{{q_{0}}})\varphi_{X} (Q - q_{0})\,- \sigma_{y} \cdot q_{0} \cdot \left({1 - \varPhi_{\varUpsilon} (z_{{q_{0}}})} \right)\varphi_{X} (Q - q_{0}) \\ & \quad - \,z_{{q_{0}}} \cdot \varphi_{\varUpsilon} (z_{{q_{0}}}) \cdot \varPhi_{X} (Q - q_{0}) - \,\sigma_{y} \cdot \varphi_{\varUpsilon} (z_{{q_{0}}}) \cdot \varphi_{X} (Q - q_{0})\\ & \quad - \sigma_{y} \cdot \,\left({1 - \varPhi_{\varUpsilon} (z_{{q_{0}}})} \right)\varPhi_{X} (Q - q_{0}) + q_{0} \cdot \,\varphi_{\varUpsilon} (z_{{q_{0}}}) \cdot \varPhi_{X} (Q - q_{0}) \\ & \quad + \sigma_{y} \cdot q_{0} \cdot \,\left({1 - \varPhi_{\varUpsilon} (z_{{q_{0}}})} \right)\varphi_{X} (Q - q_{0}) \Leftrightarrow \\ \end{aligned} $$

$$ \begin{aligned}\frac{{\partial E(BO_{T})}}{{\partial q_{0}}} &= \, - \,z_{{q_{0}}} \cdot \varphi_{\varUpsilon} (z_{{q_{0}}}) \cdot \varPhi_{X} (Q - q_{0}) - \sigma_{y} \cdot \,\left({1 - \varPhi_{\varUpsilon} (z_{{q_{0}}})} \right)\varPhi_{X} (Q - q_{0}) \\&\quad+ q_{0} \cdot \,\varphi_{\varUpsilon} (z_{{q_{0}}}) \cdot \varPhi_{X} (Q - q_{0})\end{aligned} $$

$$ \begin{aligned} \frac{{\partial E(OH_{T})}}{{\partial q_{0}}} & = - \sigma_{y} \cdot q_{0} \cdot \varPhi_{\varUpsilon} (z_{{q_{0}}}) \cdot \varphi_{X} (Q - q_{0}) \cdot \frac{{\partial (Q - q_{0})}}{{\partial q_{0}}} + \left({\mu_{y} - \sigma_{y} \cdot \varphi_{\varUpsilon} (z_{{q_{0}}})} \right)\\&\quad \cdot \varphi_{X} (Q - q_{0}) \cdot \frac{{\partial (Q - q_{0})}}{{\partial q_{0}}} + \sigma_{y} \cdot \varPhi_{\varUpsilon} (z_{{q_{0}}}) \cdot \varPhi_{X} (Q - q_{0}) + \sigma_{y} \cdot q_{0} \cdot \frac{1}{{\sigma_{y}}} \\ & \quad\cdot \varphi_{\varUpsilon} (z_{{q_{0}}}) \cdot \varPhi_{X} (Q - q_{0}) + \sigma_{y} \cdot q_{0} \cdot \varPhi_{\varUpsilon} (z_{{q_{0}}}) \cdot \varphi_{X} (Q - q_{0}) \cdot \frac{{\partial (Q - q_{0})}}{{\partial q_{0}}} \\ & \quad - z_{{q_{0}}} \cdot \sigma_{y} \cdot \frac{1}{{\sigma_{y}}} \cdot \varphi_{\varUpsilon} (z_{{q_{0}}}) \cdot \varPhi_{X} (Q - q_{0}) - \left({\mu_{y} - \sigma_{y} \cdot \varphi_{\varUpsilon} (z_{{q_{0}}})} \right) \cdot \varphi_{X} (Q - q_{0})\\ & \quad \cdot \frac{{\partial (Q - q_{0})}}{{\partial q_{0}}} \\ & = \sigma_{y} \cdot q_{0} \cdot \varPhi_{\varUpsilon} (z_{{q_{0}}}) \cdot \varphi_{X} (Q - q_{0}) - \left({\mu_{y} - \sigma_{y} \cdot \varphi_{\varUpsilon} (z_{{q_{0}}})} \right) \cdot \varphi_{X} (Q - q_{0}) \\ & \quad+ \sigma_{y} \cdot \varPhi_{\varUpsilon} (z_{{q_{0}}}) \cdot \varPhi_{X} (Q - q_{0}) + q_{0} \cdot \varphi_{\varUpsilon} (z_{{q_{0}}}) \cdot \varPhi_{X} (Q - q_{0})\\ & \quad - \sigma_{y} \cdot q_{0} \cdot \varPhi_{\varUpsilon} (z_{{q_{0}}}) \cdot \varphi_{X} (Q - q_{0}) - z_{{q_{0}}} \cdot \varphi_{\varUpsilon} (z_{{q_{0}}}) \cdot \varPhi_{X} (Q - q_{0}) \\ & \quad + \left({\mu_{y} - \sigma_{y} \cdot \varphi_{\varUpsilon} (z_{{q_{0}}})} \right) \cdot \varphi_{X} (Q - q_{0}) \Leftrightarrow \\ \end{aligned} $$

$$\begin{aligned} \frac{{\partial E(OH_{T})}}{{\partial q_{0}}}& = \sigma_{y} \cdot \varPhi_{\varUpsilon} (z_{{q_{0}}}) \cdot \varPhi_{X} (Q - q_{0})\\ & \quad + q_{0} \cdot \varphi_{\varUpsilon} (z_{{q_{0}}}) \cdot \varPhi_{X} (Q - q_{0}) - z_{{q_{0}}} \cdot \varphi_{\varUpsilon} (z_{{q_{0}}}) \cdot \varPhi_{X} (Q - q_{0}) \end{aligned} $$

$$ \begin{aligned} \frac{{\partial E(Sales_{T})}}{{\partial q_{0}}} & = - \sigma_{y} \cdot Q \cdot \left({1 - \varPhi_{\varUpsilon} (z_{{q_{0}}})} \right) \cdot \varphi_{X} (Q - q_{0}) \cdot \frac{{\partial (Q - q_{0})}}{{\partial q_{0}}} \\ & \quad - \sigma_{y} \cdot \left({Q - q_{0}} \right) \cdot \varPhi_{\varUpsilon} (z_{{q_{0}}}) \cdot \,\varphi_{X} (Q - q_{0}) \cdot \frac{{\partial (Q - q_{0})}}{{\partial q_{0}}}\\ & \quad - \left({\mu_{y} - \sigma_{y} \cdot \varphi_{\varUpsilon} (z_{{q_{0}}})} \right) \cdot \,\varphi_{X} (Q - q_{0}) \cdot \frac{{\partial (Q - q_{0})}}{{\partial q_{0}}} \\ & \quad - \sigma_{y} \cdot \int_{0}^{{Q - q_{0}}} {x \cdot \varphi_{\varUpsilon} (z_{{q_{0}}}) \cdot \frac{1}{{\sigma_{y}}} \cdot \varphi_{X} (x)} \cdot dx\\ & \quad + \sigma_{y} \cdot \left({Q - q_{0}} \right) \cdot \left({1 - \varPhi_{\varUpsilon} (z_{{q_{0}}})} \right) \cdot \varphi_{X} (Q - q_{0}) \cdot \frac{{\partial (Q - q_{0})}}{{\partial q_{0}}} \\ & \quad + \sigma_{y} \cdot \left({1 - \varPhi_{\varUpsilon} (z_{{q_{0}}})} \right) \cdot \varPhi_{X} (Q - q_{0}) - q_{0} \cdot \varphi_{\varUpsilon} (z_{{q_{0}}}) \cdot \varPhi_{X} (Q - q_{0}) \\ & \quad- \sigma_{y} \cdot q_{0} \cdot \left({1 - \varPhi_{\varUpsilon} (z_{{q_{0}}})} \right) \cdot \varphi_{X} (Q - q_{0}) \\ & \quad + \int_{0}^{{Q - q_{0}}} {\sigma_{y} \cdot x \cdot \varphi_{\varUpsilon} (z_{{q_{0}}}) \cdot \frac{1}{{\sigma_{y}}} \cdot \varphi_{X} (x) \cdot dx} - \,\sigma_{y} \cdot \left({Q - q_{0}} \right) \cdot \varPhi_{\varUpsilon} (z_{{q_{0}}}) \\ & \quad \cdot \varphi_{X} (Q - q_{0})+ \left({z_{{q_{0}}} \cdot \varphi_{\varUpsilon} (z_{{q_{0}}})} \right)\varPhi_{X} (Q - q_{0}) \\ & \quad - \left({\mu_{y} - \sigma_{y} \cdot \varphi_{\varUpsilon} (z_{{q_{0}}})} \right) \cdot \varphi_{X} (Q - q_{0}) \Leftrightarrow \\ \end{aligned} $$

$$\begin{aligned} \frac{{\partial E(Sales_{T})}}{{\partial q_{0}}} &= \sigma_{y} \cdot \left({1 - \varPhi_{\varUpsilon} (z_{{q_{0}}})} \right) \cdot \varPhi_{X} (Q - q_{0}) - q_{0} \cdot \varphi_{\varUpsilon} (z_{{q_{0}}}) \cdot \varPhi_{X} (Q - q_{0})\\&\quad + \left({z_{{q_{0}}} \cdot \varphi_{\varUpsilon} (z_{{q_{0}}})} \right)\varPhi_{X} (Q - q_{0})\end{aligned} $$

By applying the first order conditions leads to:

$$ \left(\begin{aligned} \left({p - c + b} \right) \cdot \sigma_{y} - \left({p - s + b} \right) \cdot \sigma_{y} \cdot \varPhi_{\varUpsilon} (z_{{q_{0}}}) \hfill \\ - \left({p - s + b} \right) \cdot q_{0} \cdot \varphi_{\varUpsilon} (z_{{q_{0}}}) + \left({p - s + b} \right) \cdot z_{{q_{0}}} \cdot \varphi_{\varUpsilon} (z_{{q_{0}}}) \hfill \\ \end{aligned} \right) \cdot \varPhi_{X} (Q - q_{0}) = 0 \Leftrightarrow $$

$$ \left(\begin{aligned} \left({p - c + b} \right) \cdot \sigma_{y} - \left({p - s + b} \right) \cdot \sigma_{y} \cdot \varPhi_{\varUpsilon} (z_{{q_{0}}}) \hfill \\ - \left({p - s + b} \right) \cdot q_{0} \cdot \varphi_{\varUpsilon} (z_{{q_{0}}}) + \left({p - s + b} \right) \cdot z_{{q_{0}}} \cdot \varphi_{\varUpsilon} (z_{{q_{0}}}) \hfill \\ \end{aligned} \right) = 0 $$

Finally, by solving with respect to $q_{0}$, further leads to

$$ q_{0} = \frac{{\left({p - c + b} \right)}}{{\left({p - s + b} \right)}} \cdot \frac{{\sigma_{y}}}{{\varphi_{\varUpsilon} (z_{{q_{0}}})}} - \frac{{\sigma_{y} \cdot \varPhi_{\varUpsilon} (z_{{q_{0}}})}}{{\varphi_{\varUpsilon} (z_{{q_{0}}})}} + z_{{q_{0}}} $$

In order to prove that the first order conditions are satisfied, then:$\frac{{\partial^{2} E(Profit_{T})}}{{(\partial q_{0})^{2}}} < 0$. Thus

$$ \begin{aligned} \frac{{\partial^{2} E(Profit_{T})}}{{(\partial q_{0})^{2}}} & = - \left({p - s + b} \right) \cdot \sigma_{y} \cdot \varphi_{\varUpsilon} (z_{{q_{0}}}) \cdot \frac{1}{{\sigma_{y}}} - \left({p - s + b} \right) \cdot \varphi_{\varUpsilon} (z_{{q_{0}}})\\ & \quad + \left({p - s + b} \right) \cdot q_{0} \cdot z_{{q_{0}}} \cdot \varphi_{\varUpsilon} (z_{{q_{0}}}) \cdot \frac{1}{{\sigma_{y}}} \\ & \quad + \left({p - s + b} \right) \cdot \frac{1}{{\sigma_{y}}} \cdot \varphi_{\varUpsilon} (z_{{q_{0}}}) - \left({p - s + b} \right) \cdot \left({z_{{q_{0}}}} \right)^{2} \cdot \varphi_{\varUpsilon} (z_{{q_{0}}}) \cdot \frac{1}{{\sigma_{y}}} < 0 \\ \end{aligned} $$

As $(p - s + b) \cdot {\varphi_{\varUpsilon}} ({z_{q_{0}}})$ is always positive, the first order conditions are satisfied if and only if the following inequality is also satisfied:

$$ q_{0} \cdot z_{{q_{0}}} < \left({z_{{q_{0}}}} \right)^{2} + 2 \cdot \sigma_{y} - 1 $$