Abstract
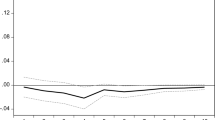
Liquidity risk is the risk that an asset cannot always be sold without causing a fall in its price because of a lack of demand for this asset. Many empirical studies examining liquidity premia have focused on government bonds. In this paper, we specifically investigate the yield differentials between liquid and illiquid German covered bonds by considering the yields of traditional Pfandbrief bonds and Jumbo Pfandbrief bonds with different maturities. In terms of credit risk the spread between the yields of these two types of covered bonds should be zero. Moreover, assuming that the liquidity risk premium is a stationary variable the yields of Pfandbrief bonds and Jumbo Pfandbrief bonds (which seem to be integrated of order one) should be cointegrated. We make use of the methodology proposed in the related field of fractional integrated models to conduct our empirical analysis. Due to the 2008–2009 global financial crisis, it also seems to be appropriate to consider structural change. To the extent that the European Central Bank has started to purchase covered bonds under the crisis pressure, our empirical evidence would have a high relevance for monetary policymakers as far as the liquidity risk is concerned. Here, our results indicate fractionally cointegrated yields before and after the crisis, while the degree of integration of the spread increases strongly during the crisis.

(Source: European Central Bank)

(Source: The German Pfandbrief Banks)




Similar content being viewed by others
References
Bandi, F. M., & Perron, B. (2006). Long memory and the relation between implied and realized volatility. Journal of Financial Econometrics, 4, 636–670.
Basse, T., Wegener, C., & Kunze, F. (2018). Government bond yields in germany and spain—Empirical evidence from better days. Quantitative Finance, 18, 827–835.
Bierens, H. J., & Martins, L. F. (2010). Time-varying cointegration. Econometric Theory, 26, 1453–1490.
Boesel, N., Kool, C., & Lugo, S. (2018). Do european banks with a covered bond program issue asset-backed securities for funding? Journal of International Money and Finance, 81, 76–87.
Boudoukh, J., & Whitelaw, R. F. (1993). Liquidity as a choice variable: A lesson from the japanese government bond market. Review of Financial Studies, 6, 265–292.
Carriero, V. (2017). Bank rescues and legal challenges: The case of bail in. European Business Law Review, 28, 635–647.
Christensen, B. J., & Nielsen, M. Ø. (2006). Asymptotic normality of narrow-band least squares in the stationary fractional cointegration model and volatility forecasting. Journal of Econometrics, 133, 343–371.
Covi, G. (2017). The emerging regulatory landscape: A new normal. Journal of Banking Regulation, 18, 233–255.
Fawley, B. W., & Neely, C. J. (2013). Four stories of quantitative easing. Federal Reserve Bank of St. Louis Review, 95, 51–88.
Fratzscher, M. (2002). Financial market integration in europe: On the effects of emu on stock markets. International Journal of Finance & Economics, 7, 165–193.
Frömmel, M., & Kruse, R. (2015). Interest rate convergence in the ems prior to european monetary union. Journal of Policy Modeling, 37, 990–1004.
Geweke, J., & Porter-Hudak, S. (1983). The estimation and application of long memory time series models. Journal of Time Series Analysis, 4, 221–238.
Goldreich, D., Hanke, B., & Nath, P. (2005). The price of future liquidity: Time-varying liquidity in the us treasury market. Review of Finance, 9, 1–32.
Gürtler, M., & Neelmeier, P. (2018a). Empirical analysis of the international public covered bond market. Journal of Empirical Finance, 46, 163–181.
Gürtler, M., & Neelmeier, P. (2018b). Risk assessment of mortgage covered bonds: International evidence. Finance Research Letters. (Forthcoming).
Hagen, L. (2003). Covered bond—das unbekannte wesen. In Verband Deutscher Hypothekenbanken (ed.): The Pfandbrief 2003—Facts and Figures (pp. 29–36), Berlin: VDH.
Henseler, K., & Rapp, M. S. (2018). Stock market effects of ecb’s asset purchase programmes: Firm-level evidence. Economics Letters, 169, 7–10.
Johansen, S. (1988). Statistical analysis of cointegration vectors. Journal of Economic Dynamics and Control, 12, 231–254.
Johansen, S., & Juselius, K. (1990). Maximum likelihood estimation and inference on cointegration—With applications to the demand for money. Oxford Bulletin of Economics and statistics, 52, 169–210.
Kempf, A., Korn, O., & Uhrig-Homburg, M. (2012). The term structure of illiquidity premia. Journal of Banking & Finance, 36, 1381–1391.
Koijen, R. S., Koulischer, F., Nguyen, B., & Yogo, M. (2017). Euro-area quantitative easing and portfolio rebalancing. American Economic Review, 107, 621–27.
Koziol, C., & Sauerbier, P. (2007). Valuation of bond illiquidity: An option-theoretical approach. Journal of Fixed Income, 16, 81.
Leybourne, S., Taylor, R., & Kim, T. (2007). CUSUM of squares-based tests for a change in persistence. Journal of Time Series Analysis, 28, 408–433.
Lorenz, M. (2006). Pfandbriefe versus mbs—Rivals, or complementary instruments? In Verband Deutscher Hypothekenbanken (ed.): The Pfandbrief 2006—Facts and Figures (pp. 47–57). Berlin: VDP.
Lucas, R. E. (1990). Liquidity and interest rates. Journal of Economic Theory, 50, 237–264.
Markmann, H., & Zietz, J. (2017). Determining the effectiveness of the eurosystem’s covered bond purchase programs on secondary markets. The Quarterly Review of Economics and Finance, 66, 314–327.
Ng, S., & Perron, P. (2001). Lag length selection and the construction of unit root tests with good size and power. Econometrica, 69, 1519–1554.
Nielsen, M. Ø., & Frederiksen, P. (2011). Fully modified narrow-band least squares estimation of weak fractional cointegration. The Econometrics Journal, 14, 77–120.
Phillips, P. C., & Magdalinos, T. (2007). Limit theory for moderate deviations from a unit root. Journal of Econometrics, 136, 115–130.
Prokopczuk, M., Siewert, J. B., & Vonhoff, V. (2013). Credit risk in covered bonds. Journal of Empirical Finance, 21, 102–120.
Prokopczuk, M., & Vonhoff, V. (2012). Risk premia in covered bond markets. The Journal of Fixed Income, 22, 19.
Qu, Z. (2011). A test against spurious long memory. Journal of Business & Economic Statistics, 29, 423–438.
Robinson, P. M. (2008). Multiple local whittle estimation in stationary systems. The Annals of Statistics, 36, 2508–2530.
Schwarcz, S. L. (2010). The conundrum of covered bonds. Business Lawyer, 66, 561.
Shimotsu, K. (2010). Exact local whittle estimation of fractional integration with unknown mean and time trend. Econometric Theory, 26, 501.
Shimotsu, K. (2012). Exact local whittle estimation of fractionally cointegrated systems. Journal of Econometrics, 169, 266–278.
Shimotsu, K., & Phillips, P. C. (2005). Exact local whittle estimation of fractional integration. The Annals of Statistics, 33, 1890–1933.
Sibbertsen, P., & Kruse, R. (2009). Testing for a break in persistence under long-range dependencies. Journal of Time Series Analysis, 30, 263–285.
Sibbertsen, P., Wegener, C., & Basse, T. (2014). Testing for a break in the persistence in yield spreads of emu government bonds. Journal of Banking & Finance, 41, 109–118.
Tolckmitt, J., & Walburg, C. (2002). The pfandbrief in the european capital market. In: Verband Deutscher Hypothekenbanken (ed.): The Pfandbrief 2002—Facts and figures (pp. 7–31). Berlin: VDP.
Trichet, J.-C. (2010). State of the union: The financial crisis and the ecb’s response between 2007 and 2009. JCMS: Journal of Common Market Studies, 48, 7–19.
Velasco, C. (2003). Gaussian semi-parametric estimation of fractional cointegration. Journal of Time Series Analysis, 24, 345–378.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
We would like to thank the participants of the Paris Financial Management Conference 2016 and the participants of the Annual International Conference on Macroeconomic Analysis and International Finance 2017 for insightful discussions. Furthermore, we would like to thank the editor and two anonymous referees for helpfull comments and suggestions.
Rights and permissions
About this article
Cite this article
Wegener, C., Basse, T., Sibbertsen, P. et al. Liquidity risk and the covered bond market in times of crisis: empirical evidence from Germany. Ann Oper Res 282, 407–426 (2019). https://doi.org/10.1007/s10479-019-03326-8
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10479-019-03326-8