Statistical estimation of operating reserve requirements using rolling horizon stochastic optimization

Abstract

We develop a multi-period stochastic optimization framework for identifying operating reserve requirements in power systems with significant penetration of renewable energy resources. Our model captures different types of operating reserves, uncertainty in renewable energy generation and demand, and differences in generator operation time scales. Along with planning for reserve capacity, our model is designed to provide recommendations about base-load generation in a non-anticipative manner, while power network and reserve utilization decisions are made in an adaptive manner. We propose a rolling horizon framework with look-ahead approximation in which the optimization problem can be written as a two-stage stochastic linear program (2-SLP) in each time period. Our 2-SLPs are solved using a sequential sampling method, stochastic decomposition, which has been shown to be effective for power system optimization. Further, as market operations impose strict time requirements for providing dispatch decisions, we propose a warm-starting mechanism to speed up this algorithm. Our experimental results, based on IEEE test systems, establish the value of our stochastic approach when compared both to deterministic rules from the literature and to current practice. The resulting computational improvements demonstrate the applicability of our approach to real power systems.

Appendices

Statistical model of uncertainty

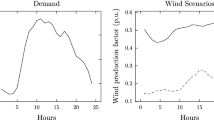
Wind power at any wind farm location can be described as a stochastic process. This process exhibits spatial correlation with processes describing wind power at other geographically separated wind farm locations. These processes are also temporally correlated across several time periods. Hence an appropriate description of these stochastic processes requires recognizing the spatio-temporal correlations of these processes.

The available wind power data is pre-processed by identifying the trend and seasonality. The seasonal-trend decomposition procedure based on loses [STL, Cleveland et al. (1990)] is an appropriate method to achieve this. Once trend and seasonality is estimated, they are subtracted from the original time-series to obtain the residual time-series. Before proceeding, it is necessary to verify if this residual series is stationary. The Augmented Dick–Fuller test and KPSS test were used for this purpose (Hamilton 1994). One possible choice to model a stationary time-series is the multivariate ARMA process shown in (12). A multivariate ARMA models was fitted using the MTS package (Tsay 2005) in R. The order selection is based on Bayesian information criterion (BIC) as it is most suitable for data with limited length. The validity of the model is verified by checking the cross-covariance and correlation functions, and the whiteness of the residual process is verified using the Ljung–Box test.

Recall that our optimization framework relies upon a constant stream of simulated scenarios. The fitted ARMA model is used for this purpose. The simulation is carried out at fine timescale within the decision epoch $t\in \mathcal {T}$. Recall that we introduce time index $\tau$ in Sect. 2.5 to unify different time scales. At corresponding time index $\tau$ at time period $t\in \mathcal {T}$, we used historical data from time period $(\tau -1)$ as known information for this simulation (the red time series in Fig. 4). Once a residual time series is simulated, the estimated trend and seasonality is added back to obtain the wind power time series (the blue time series in Fig. 4). It should be noted that it is possible to obtain negative wind power values (particularly when trend values are small) using the above procedure. In order to address this, we truncate the simulated time series at zero: ${\widetilde{W}}_{\tau } = \eta _{\tau } + {\tilde{\omega }}_{\tau } + \kappa _{\tau }$, where $\kappa _{\tau } > 0$ when the simulated output is negative. It is necessary to emphasize the difficulty in constructing stationary processes with non-negative outcomes. There exists limited theoretical results in Tsai and Chan (2007) to address this. However, we enforce non-negativity as part of our algorithm in order to ensure model and algorithm validity.

While our presentation in this paper revolves around stationary residual processes, non-stationary processes can also be accommodated within our framework. In this sense, the proposed method is applicable in conjunction with any external simulator [e.g., the Weather Research and Forecasting model (Powers et al. 2017)].

Notations

We will use $t\in \mathcal {T}$ to index the decision epochs and $n\in \mathcal {N}$ to index the fine time periods within decision epoch t.

Sets

$\mathcal {B}$ :

Buses

$\mathcal {L}$ :

Transmission lines

$\mathcal {D}$ :

Demand nodes

$\mathcal {W}$ :

Renewable generators

$\mathcal {G}^{B}$ :

Base-load generators

$\mathcal {G}^{F}/\mathcal {G}^{S}/\mathcal {G}^{R}$ :

following/regulating/ramping reserves.

Stochastic processes

${\hat{L}}_{tni}/{\widetilde{L}}_{tni}$ :

Forecast/actual demand (MW) at $i \in \mathcal {D}$

${\widehat{W}}_{tni}/{\widetilde{W}}_{tni}$ :

Forecast/actual renewable generation (MW) at $i\in \mathcal {W}$

${\tilde{\omega }}_{t}$ :

Consolidated random vector

$\eta _{t}$ :

Trend time series.

Parameters

$V_{i}$ :

voltage (kV) of bus $i\in \mathcal {B}$

$X_{ij}$ :

Reactance of transmission line $(i,j)\in \mathcal {L}$

$c^{b}_{i}$ :

Unit generation (MW) cost of $i\in \mathcal {G}^{B}$

$c^{f}_{i}$ :

Unit generation (MW) cost of $i\in \mathcal {G}^{F}$

$c^{s}_{i}$ :

Unit generation (MW) cost of up-front dispatch $i\in \mathcal {G}^{S}$

$c^{p}_{i}$ :

Unit cost of planning regulating service (MW) on $i\in \mathcal {G}^{S}$

$d^{s}_{i}$ :

Unit cost of utilizing (MW) $i\in \mathcal {G}^{S}$

$d^{r}_{i}$ :

Unit cost of utilizing (MW) $i\in \mathcal {G}^{R}$

$\Delta {\hat{L}}^{tni}$ :

Net-demand (MW) base on available forecast of $i\in \mathcal {D}$

$p^{min},p^{max}$ :

Transmission line limitations (MW)

$\theta ^{min},\theta ^{max}$ :

Voltage angle limitations

$G_{i}^{b,min}$,$G_{i}^{b,max}$:

Min and max capacity (MW) of $i\in \mathcal {G}^{B}$

$G_{i}^{f,min}$,$G_{i}^{f,max}$:

Min and max capacity (MW) of $i\in \mathcal {G}^{F}$

$G_{i}^{s,min}$,$G_{i}^{s,max}$:

Min and max capacity (MW) of $i\in \mathcal {G}^{S}$

$\Delta G_{i}^{b,max}$,$\Delta G_{i}^{b,min}$:

Up- and down-ramping limits of $i\in \mathcal {G}^{B}$

$\Delta G_{i}^{f,max}$,$\Delta G_{i}^{f,min}$:

Up- and down-ramping limits of $i\in \mathcal {G}^{F}$

$\Delta G_{i}^{s,max}$,$\Delta G_{i}^{s,min}$:

Up- and down-ramping limits of $i\in \mathcal {G}^{S}$.

Decision variables

$x^{b}_{ti}$ :

Base-load generation (MW) at $i\in \mathcal {G}^{B}$

$x^{f}_{tni}$ :

Following reserve generation (MW) at $i\in \mathcal {G}^{F}$

$x^{s}_{ti}$ :

Up-front dispatch (MW) at $i\in \mathcal {G}^{S}$

$x^{p+}_{ti}$ :

Planned regulating-up service (MW) at $i\in \mathcal {G}^{S}$

$x^{p-}_{ti}$ :

Planned regulating-down service (MW) at $i\in \mathcal {G}^{S}$

$p_{tnij}$ :

Power flow (MW) on line $(i,j)\in \mathcal {L}$

$\theta _{tni}$ :

Voltage angle at $i\in \mathcal {B}$

$u^{s}_{tni}$ :

Utilization spinning reserves (MW) $i\in \mathcal {G}^{S}$

$u^{r}_{tni}$ :

Utilization of ramping reserve (MW) $i\in \mathcal {G}^{R}$

$x_{t}$ :

Consolidated first-stage decision vector $=[(x_{ti}^{b})_{i\in \mathcal {G}^{B}},(x_{ti}^{f})_{i\in \mathcal {G}^{F}},(x_{ti}^{s})_{i\in \mathcal {G}^{S}},(x_{ti}^{p})_{i\in \mathcal {G}^{S}}]$)

$y_{t}$ :

Consolidated second-stage decision vector $=[(p_{tnij})_{(i,j)\in \mathcal {L}}, (\theta _{tni})_{i\in \mathcal {B}},(u_{tni}^{s})_{i\in \mathcal {G}^{S}},(u_{tni}^{r})_{i\in \mathcal {G}^{R}}]$)

$s_{t}$ :

State variable ($=[x_{t-1},y_{t-1}({\bar{\omega }}_{t-1})]$).