Skip to main content
Springer Nature Link
Log in

Analysis of the waiting time distribution in M/G/1 retrial queues with two way communication

  • S.I.: QueueStochMod2019
  • Published:
Annals of Operations Research Aims and scope Submit manuscript

Abstract

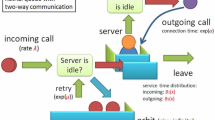
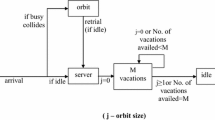
We consider an M/G/1 retrial queue in which there are two types of calls: ingoing calls made by regular customers and outgoing calls made by the server in idle time. The service times of ingoing calls and outgoing calls have different arbitrary distributions. In this paper, we are interested in the analysis of the waiting time distribution. We obtain an equation for the joint transform of the number of ingoing calls in the orbit and the waiting time of an arbitrary ingoing call. Using this result, we can obtain the moments of the waiting time distribution of an arbitrary ingoing call.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

References

  • Artalejo, J. R. (1999a). A classified bibliography of research on retrial queues: Progress in 1990–1999. Top, 7, 187–211.

    Article  Google Scholar 

  • Artalejo, J. R. (1999b). Accessible bibliography on retrial queues. Mathematical and Computer Modelling, 30, 1–6.

    Article  Google Scholar 

  • Artalejo, J. R. (2010). Accessible bibliography on retrial queues: Progress in 2000–2009. Mathematical and Computer Modelling, 51, 1071–1081.

    Article  Google Scholar 

  • Artalejo, J. R., Falin, G. I., & Lopez-Herrero, M. J. (2002). A second order analysis of the waiting time in the M/G/1 retrial queue. Asia-Pacific Journal of Operational Research, 19, 131–148.

    Google Scholar 

  • Artalejo, J. R., & Gómez-Corral, A. (2008). Retrial Queueing Systems. Berlin: Springer.

    Book  Google Scholar 

  • Artalejo, J. R., & Phung-Duc, T. (2012). Markovian retrial queues with two way communication. Journal of Industrial and Management Optimization, 8, 781–806.

    Article  Google Scholar 

  • Artalejo, J. R., & Phung-Duc, T. (2013). Single server retrial queues with two way communication. Applied Mathematical Modelling, 37, 1811–1822.

    Article  Google Scholar 

  • Artalejo, J. R., & Resing, J. A. C. (2010). Mean value analysis of single server retrial queues. Asia-Pacific Journal of Operational Research, 27, 335–345.

    Article  Google Scholar 

  • Falin, G. I. (1979). Model of coupled switching in presence of recurrent calls. Engineering Cybernetics Review, 17, 53–59.

    Google Scholar 

  • Falin, G. I. (1990). A survey of retrial queues. Queueing Systems, 7, 127–168.

    Article  Google Scholar 

  • Falin, G. I., & Templeton, J. G. C. (1997). Retrial queues. London: Chapman & Hall.

    Book  Google Scholar 

  • Kim, B., & Kim, J. (2011). Higher moments of the waiting time distribution in M/G/1 retrial queues. Operations Research Letters, 39, 224–228.

    Article  Google Scholar 

  • Kim, J., & Kim, B. (2016). A survey of retrial queueing systems. Annals of Operations Research, 247, 3–36.

    Article  Google Scholar 

  • Kulkarni, V. G., & Liang, H. M. (1997). Retrial queues revisited. In J. H. Dshalalow (Ed.), Frontiers in queueing: models and applications in science and engineering (pp. 19–34). Boca Raton: CRC Press.

    Google Scholar 

  • Nazarov, A., Phung-Duc, T., & Paul, S. (2019). Slow retrial asymptotics for a single server queue with two-way communication and Markov modulated Poisson input. Journal of Systems Science and Systems Engineering, 28, 181–193.

    Article  Google Scholar 

  • Sakurai, H., & Phung-Duc, T. (2015). Two-way communication retrial queues with multiple types of outgoing calls. Top, 23, 466–492.

    Article  Google Scholar 

  • Sakurai, H., & Phung-Duc, T. (2016). Scaling limits for single server retrial queues with two-way communication. Annals of Operations Research, 247, 229–256.

    Article  Google Scholar 

  • Takagi, H. (1991). Queueing analysis, volume 1: Vacation and priority systems, part 1. Amsterdam: North-Holland.

    Google Scholar 

  • Yang, T., & Templeton, J. G. C. (1987). A survey on retrial queues. Queueing Systems, 2, 201–233.

    Article  Google Scholar 

Download references

Acknowledgements

We are grateful to the reviewers for valuable comments and suggestions. S.W. Lee’s research was supported by the Pukyong National University Research Fund in 2019 (C-D-2019-1249). B. Kim’s research was supported by the National Research Foundation of Korea (NRF) Grant funded by the Korea government(MSIT) (No. 2020R1A2B5B01001864). J. Kim’s research was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (No. 2020R1F1A1A01065568).

Author information

Authors and Affiliations

  1. Division of Business Administration, Pukyong National University, 45 Yongso-ro, Nam-gu, Busan, 48513, Korea

    Se Won Lee

  2. Department of Mathematics, Korea University, 145 Anam-ro, Seongbuk-gu, Seoul, 02841, Korea

    Bara Kim

  3. Department of Mathematics Education, Chungbuk National University, 1 Chungdae-ro, Seowon-gu, Cheongju, Chungbuk, 28644, Korea

    Jeongsim Kim

Authors
  1. Se Won Lee
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Bara Kim
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Jeongsim Kim
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Jeongsim Kim.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Lee, S.W., Kim, B. & Kim, J. Analysis of the waiting time distribution in M/G/1 retrial queues with two way communication. Ann Oper Res 310, 505–518 (2022). https://doi.org/10.1007/s10479-020-03717-2

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10479-020-03717-2

Keywords