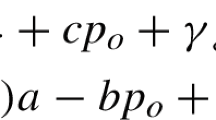Resale value guaranteed strategy, information sharing and electric vehicles adoption

Abstract

A resale value guaranteed (RVG) strategy has emerged as a novel way to alleviate EV purchasers’ resale anxiety. However, certain questions, such as when to initiate a RVG strategy and whether to share information with supply chain partners, are unanswered. In this study, we aim to investigate the impacts of a RVG strategy and reliability of a RVG decision on EV adoption and supply chain performance. We develop analytical models to analyze the optimal RVG strategy in asymmetric versus symmetric information situations, using the traditional business model as a benchmark. The results indicate that a RVG strategy can be an effective way to increase supply chain profits for products that are subject to a degree of resale anxiety, trade-in cost, and the reliability of the manufacturer’s commitments. Incentives provided by one party to the other can be utilized to encourage information sharing. However, information sharing does not necessarily lead to higher sales volume.

Appendix

1.1 Proof of Lemma 1

• (1) Since $\pi_{r} = (p_{r} - w)q_{r} = (p_{r} - w)(a - bp_{r} )$, we have $p_{r}^{*} = \frac{a + bw}{2b}$ and $q_{r}^{*} = \frac{a - bw}{2}$. In addition, $Eq(w) = \Pr (\rho \left| {\varphi_{s} } \right.)\alpha q_{s}^{*} + \Pr (\rho \left| {\varphi_{r} } \right.)\alpha q_{s}^{*} + \Pr (\rho \left| {\varphi_{s} } \right.)(1 - \alpha )q_{r} + \Pr (\rho \left| {\varphi_{r} } \right.)(1 - \alpha )q_{r} = [I + 2(1 - I)\gamma ]\frac{2a - (2b + \beta )w}{2}$. Hence $\pi_{m}^{A} = (w - c)Eq - \eta \xi q_{r}^{*} = (w - c)\left[ {[I + 2(1 - I)\gamma ]\frac{2a - (2b + \beta )w}{2}} \right] - \eta \xi \frac{a - bw}{2}$. Using the first order condition of π_m with respect to w, we have the result $w_{r}^{A*} = \frac{a}{2b + \beta } + \frac{\eta \xi b}{2[I + 2(1 - I)\gamma ](2b + \beta )} + \frac{c}{2}$.

• (2) Replacing $w_{r}^{A*}$ with w in $p_{r}^{*} = \frac{a + bw}{2b}$, we have the result.

• (3) Replacing $w_{r}^{A*}$ with w in $q_{r}^{*} = \frac{a - bw}{2}$, we have the result.

• (4) Since $\pi_{r}^{A*} = (p_{r}^{*} - w_{r}^{*} )q_{r}^{*} = \frac{{(a - bw_{r}^{*} )^{2} }}{4b}$, replacing $w_{r}^{A*}$, we have the result for $\pi_{r}^{A*}$. In a similar way, since $\pi_{m}^{A*} = (w_{r}^{*} - c)\left[ {[I + 2(1 - I)\gamma ]\frac{{2a - (2b + \beta )w_{r}^{*} }}{2}} \right] - \eta \xi \frac{{a - bw_{r}^{*} }}{2}$, replacing $w_{r}^{A*}$, we have the results for $\pi_{m}^{A*}$.□

1.2 Proof of Proposition 1

In a traditional selling business, the demand function is $q_{s} = a - bp_{s} - \beta p_{s}$. The dealer’s profit function is $\pi_{sr} = (p_{s} - w)(a - bp_{s} - \beta p_{s} )$, and the manufacturer’s profit function is $\pi_{sm} = (w - c)q_{s}$. Then we can see that the maximum profit of the manufacturer, $\pi_{sm}^{*}$, is $\pi_{sm}^{*} = \frac{{[a - (b + \beta )c]^{2} }}{8(b + \beta )}$, and the maximum profit of the dealer, $\pi_{sr}^{*}$, is $\pi_{sr}^{*} = \frac{{[a - (b + \beta )c]^{2} }}{16(b + \beta )}$. We can further obtain the optimal sales volume $q_{s}^{*}$, the unit retail price $p_{s}^{*}$, and the unit wholesale price $w_{s}^{*}$, which are $q_{s}^{*} = \frac{a - (b + \beta )c}{4}$, $p_{s}^{*} = \frac{3a + (b + \beta )c}{4(b + \beta )}$, and $w_{s}^{*} = \frac{a + (b + \beta )c}{2(b + \beta )}$, respectively.

With a RVG strategy, the demand function becomes $q_{r} = a - bp_{r}$. Even if the dealer agrees to follow the manufacturer’s RVG proposal, the manufacturer needs to account for the possibility that the dealer’s consumer information is not accurate. Hence the manufacturer’s profit function becomes $\pi_{m}^{A} = (w - c)Eq - \eta \xi q_{r}$, where $Eq(w) = \Pr (\rho \left| {\varphi_{s} } \right.)q_{s}^{*} + \Pr (\rho \left| {\varphi_{r} } \right.)q_{s}^{*} + \Pr (\rho \left| {\varphi_{s} } \right.)q_{r} + \Pr (\rho \left| {\varphi_{r} } \right.)q_{r}$, as shown in Sect. 3. The dealer’s profit is $\pi_{r}^{A} = (p_{r} - w)(a - bp_{r} )$ if the dealer agrees to initiate the RVG strategy. Hence we can obtain the maximum profit of the manufacturer $\pi_{m}^{A*}$, i.e., $\pi_{m}^{A*} = \frac{{[I + 2(1 - I)\gamma ]\left[ {2a - (2b + \beta )c} \right]^{2} }}{8(2b + \beta )} + \frac{\eta \xi b(2a + (2b + \beta )c)}{4(2b + \beta )} + \frac{{(\eta \xi b)^{2} }}{8[I + 2(1 - I)\gamma ](2b + \beta )} - \frac{\eta \xi a}{2}$.

Solving the inequality $\pi_{m}^{A*} > \pi_{sm}^{*}$, we obtain the result.□

1.3 Proof of Proposition 2

• (1) Because $\frac{{\partial \pi_{m}^{A*} }}{\partial \beta } = - \frac{{[I + 2(1 - I)\gamma ]\left[ {2a - (2b + \beta )c} \right]c}}{4(2b + \beta )} - \frac{{[I + 2(1 - I)\gamma ]\left[ {2a - (2b + \beta )c} \right]^{2} }}{{8(2b + \beta )^{2} }} - \frac{\eta \xi ab}{{2(2b + \beta )^{2} }} - \frac{{(\eta \xi b)^{2} }}{{8[I + 2(1 - I)\gamma ](2b + \beta )^{2} }} < 0$, we have the first result in Proposition 2 (1).

  From analysis in Sect. 3, we can obtain $p_{r}^{*} = \frac{a}{2b} + \frac{2[I + 2(1 - I)\gamma ]a + \eta \xi b}{4[I + 2(1 - I)\gamma ](2b + \beta )} + \frac{[I + 2(1 - I)\gamma ]c}{4[I + 2(1 - I)\gamma ]}$. Take the first derivative of $p_{r}^{*}$ w.r.t. β, we have $\frac{{\partial p_{r}^{*} }}{\partial \beta } = - \frac{2[I + 2(1 - I)\gamma ]a + \eta \xi b}{{4[I + 2(1 - I)\gamma ](2b + \beta )^{2} }} < 0$. It is the second result in Proposition 2 (1).

  Because $q_{r}^{*} = \frac{a}{2} - \frac{{2[I + 2(1 - I)\gamma ]ab + \eta \xi b^{2} + [I + 2(1 - I)\gamma ](2b + \beta )bc}}{4[I + 2(1 - I)\gamma ](2b + \beta )}$ and $\frac{{\partial q_{r}^{*} }}{\partial \eta } = - \frac{{\xi b^{2} }}{{4\left( {I + 2(1 - I)\gamma } \right)(2b + \beta )}} < 0$, we have the third result in Proposition 2 (1).

• (2) Because $\frac{{\partial \pi_{m}^{A*} }}{\partial \eta } = \frac{{\xi b(2a + (2b + \beta )c)[I + 2(1 - I)\gamma ] + \eta \xi^{2} b^{2} - 2[I + 2(1 - I)\gamma ](2b + \beta )\xi a}}{4[I + 2(1 - I)\gamma ](2b + \beta )}$, $\frac{{\partial \pi_{m}^{A*} }}{\partial \eta } < 0$ when $\eta < \frac{[I + 2(1 - I)\gamma ][2ab + 2\beta a - (2b + \beta )bc]}{{\xi b^{2} }}$. We have the result in Proposition 2 (2).

• (3) Because $\frac{{\partial \pi_{m}^{A *} }}{\partial I} = \frac{{\left( {\left( {2a - (2b + \beta )c} \right)\left( {I + 2(1 - I)\gamma } \right) + \eta \xi b} \right)\left( {\left( {2a - (2b + \beta )c} \right)\left( {I + 2(1 - I)\gamma } \right) - \eta \xi b} \right)(1 - 2\gamma )}}{{8\left( {I + 2(1 - I)\gamma } \right)^{2} (2b + \beta )}}$, when $\left( {2a - (2b + \beta )c} \right)\left( {I + 2(1 - I)\gamma } \right) - \eta \xi b > 0$, i.e., $I > \frac{2\gamma (2a - 2bc - c\beta ) - \eta \xi b}{{\left( {2a - (2b + \beta )c} \right)(2\gamma - 1)}}$, we have the result in Proposition 2 (3).

• (4) Because $q_{r}^{*} = \frac{a}{2} - \frac{{2[I + 2(1 - I)\gamma ]ab + \eta \xi b^{2} + [I + 2(1 - I)\gamma ](2b + \beta )bc}}{4[I + 2(1 - I)\gamma ](2b + \beta )}$, and $\frac{{\partial q_{r}^{A*} }}{\partial I} = \frac{{\eta \xi b^{2} (1 - 2\gamma )}}{{4[I + 2(1 - I)\gamma ]^{2} (2b + \beta )}}$, when γ < ½, we have $\frac{{\partial q_{r}^{A*} }}{\partial I} > 0$. Otherwise, $\frac{{\partial q_{r}^{A*} }}{\partial I} < 0$.□

1.4 Proof of Proposition 3

Because $\pi_{r}^{S*} = (p_{r}^{S*} - w_{{}}^{S*} )q_{r}^{S*} + A = \frac{{\left( {\frac{a - bc}{2} - \frac{\eta \xi b}{{2\left( {I + \gamma (1 - I)} \right)}}} \right)^{2} }}{4b} + A$, and because $\pi_{r}^{A*} = \frac{{\left( {\frac{a(b+\beta)}{2(b+\beta)} - \frac{\eta \xi b^2}{{2\left( {I + 2\gamma (1 - I)} \right) 2b+\beta}} - \frac{bc}{2}} \right)^{2} }}{4b}$, solving A from $\pi_{r}^{S*} > \pi_{r}^{A*}$, we have the result on the left-hand side. Similarly, because $\pi_{m}^{A*} = \frac{{\left( {I + 2\gamma (1 - I)} \right)\left( {2a - c(2b + \beta )} \right)^{2} }}{8(2b + \beta )} + \frac{{\eta \xi b\left( {2a + c(2b + \beta )} \right)}}{4(2b + \beta )} + \frac{{(\eta \xi b)^{2} }}{{8\left( {I + 2\gamma (1 - I)} \right)(2b + \beta )}} - \frac{\eta \xi a}{2}$, and because $\pi_{m}^{S*} = \frac{{\left( {\left( {I + 2\gamma (1 - I)} \right)a - \left( {\left( {I + 2\gamma (1 - I)} \right)c + \eta \xi } \right)b} \right)^{2} }}{{8\left( {I + 2\gamma (1 - I)} \right)b}} - A$, solving A from $\pi_{m}^{S*} > \pi_{m}^{A*}$, we have the result on the right-hand side.□

1.5 Proof of Proposition 4

• (1) The proof is obtained by solving η from comparison of $q_{r}^{S*}$ and $q_{r}^{A*}$. Because $q_{r}^{S*} = \frac{a}{2} - \frac{{a\left( {I + 2\gamma (1 - I)} \right) + b\left( {\eta \xi + c\left( {I + 2\gamma (1 - I)} \right)} \right)}}{{4\left( {I + 2\gamma (1 - I)} \right)}}$, $q_{s}^{*} = \frac{a - (b + \beta )c}{4}$, and because $q_{r}^{A*} = \frac{a}{2} - \frac{{2ab\left( {I + 2\gamma (1 - I)} \right) + \eta \xi b^{2} + bc(2b + \beta )\left( {I + 2\gamma (1 - I)} \right)}}{{4(2b + \beta )\left( {I + 2\gamma (1 - I)} \right)}}$, we have the result of Proposition 4 (1).

Similarly, we can obtain results of Proposition 4 (2) and (3). (4) The difference between $q_{r}^{S*}$ and $q_{r}^{A*}$ is $q_{r}^{A*} - q_{r}^{S*} = \frac{{\left( {I + 2\gamma (1 - I)} \right)\beta a + (b + \beta )\eta \xi b}}{{4\left( {I + 2\gamma (1 - I)} \right)(2b + \beta )}} > 0$. Then, we have the result of Proposition 4 (4).□