Skip to main content
Springer Nature Link
Log in

Cost-efficiency under inter-temporal dependence

  • Original Research
  • Published:
Annals of Operations Research Aims and scope Submit manuscript

    We’re sorry, something doesn't seem to be working properly.

    Please try refreshing the page. If that doesn't work, please contact support so we can address the problem.

Abstract

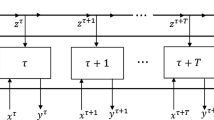
One method for evaluating cost-efficiency of commercial firms is data envelopment analysis. In the real world, data have a time dependency that also affects the cost-efficiency calculation. This article introduces a new model for measuring cost-efficiency under inter-temporal dependency in an assessment window. In the proposed approach, there is a reserve capital for the assessment window that is considered as the input of this period, and at any time of the window, a certain amount of capital is used. For practical application, the proposed model is applied to a real dataset of branches of an Iranian commercial bank to evaluate cost-efficiency under inter-temporal dependency.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  • Akther, S., Fukuyama, H., & Weber, W. L. (2013). Estimating two-stage network slacks-based inefficiency: An application to bangladesh banking. Omega, 41(1), 88–96.

    Article  Google Scholar 

  • Aparicio, J., Borras, F., Pastor, J. T., & Vidal, F. (2015). Measuring and decomposing firms revenue and cost efficiency: The Russell measures revisited. International Journal of Production Economics, 165, 19–28.

    Article  Google Scholar 

  • Ashrafi, A., & Mansouri Kaleibar, M. (2017). Cost, revenue and profit efficiency models in generalized fuzzy data envelopment analysis. Fuzzy Information and Engineering, 9(2), 237–246.

    Article  Google Scholar 

  • Avkiran, N. K. (2015). An illustration of dynamic network dea in commercial banking including robustness tests. Omega, 55, 141–150.

    Article  Google Scholar 

  • Banker, R. D., Charnes, A., & Cooper, W. W. (1984). Some models for estimating technical and scale inefficiencies in data envelopment analysis. Management Science, 30(9), 1078–1092.

    Article  Google Scholar 

  • Berger, A.N., & Humphrey, D.B. (1992). Measurement and efficiency issues in commercial banking. In Output measurement in the service sectors (pp. 245–300) University of Chicago Press.

  • Charnes, A., Cooper, W. W., & Rhodes, E. (1978). Measuring the efficiency of decision making units. European Journal of Operational Research, 2(6), 429–444.

    Article  Google Scholar 

  • Emrouznejad, A., & Thanassoulis, E. (2005). A mathematical model for dynamic efficiency using data envelopment analysis. Applied Mathematics and Computation, 160, 363–378.

    Article  Google Scholar 

  • Fare, R., & Grosskopf, S. (1996). Intertemporal production frontiers: With dynamic DEA. Amsterdam: Kluwer Academic Publishers.

    Book  Google Scholar 

  • Fare, R., Grosskopf, S., & Lovell, C. (1985). The measurement of efficiency of production. Amsterdam: Kluwer Academic Publisher.

    Book  Google Scholar 

  • Farrell, M. J. (1957). The measurement of productive efficiency. Journal of the Royal Statistical Society Series A (General), 120(3), 253–290.

    Article  Google Scholar 

  • Ferrier, G. D., & Lovell, C. A. K. (1990). Measuring cost efficiency in banking: Econometric and linear programming evidence. Journal of Econometrics, 46, 229–245.

    Article  Google Scholar 

  • Fukuyama, H., & Matousek, R. (2017). Modelling bank performance: A network dea approach. European Journal of Operational Research, 259(2), 721–732.

    Article  Google Scholar 

  • Fukuyama, H., & Weber, W. L. (2010). A slacks-based inefficiency measure for a two-stage system with bad outputs. Omega, 38(5), 398–409.

    Article  Google Scholar 

  • Ghobadi, S., Jahanshahloo, G., Lotfi, F. H., & Rostamy-Malkhalifeh, M. (2018). Efficiency measure under inter-temporal dependence. International Journal of Information Technology and Decision Making, 17(02), 657–675.

    Article  Google Scholar 

  • Holod, D., & Lewis, H. F. (2011). Resolving the deposit dilemma: A new dea bank efficiency model. Journal of Banking and Finance, 35(11), 2801–2810.

    Article  Google Scholar 

  • Jahanshahloo, G. R., & Soleimani-damaneh, M. (2006). On the pareto (dynamically) efficient paths. International Journal of Computer Mathematics, 63, 629–633.

    Google Scholar 

  • Jahanshahloo, G. R., Soleimani-damaneh, M., & Ghobadi, S. (2015). Inverse dea under inter-temporal dependence using multiple-objective programming. European Journal of Operational Research, 240, 447–456.

    Article  Google Scholar 

  • Kourtzidis, S. A., Matousek, R., & Tzeremes, N. G. (2019). Productivity growth in network models: An application to banking during the financial crisis. Journal of the Operational Research Society, 70(1), 111–124.

    Article  Google Scholar 

  • Kuosmanen, T., & Post, T. (2001). Measuring economic efficiency with incomplete price information: With an application to european commercial banks. European Journal of Operational Research, 134(1), 43–58.

    Article  Google Scholar 

  • Lozano, S. (2016). Slacks-based inefficiency approach for general networks with bad outputs: An application to the banking sector. Omega, 60, 73–84.

    Article  Google Scholar 

  • Mahmoudabadi, M. Z., & Emrouznejad, A. (2019). Comprehensive performance evaluation of banking branches: A three-stage slacks-based measure (SBM) data envelopment analysis. International Review of Economics and Finance, 64, 359–376.

    Article  Google Scholar 

  • Mostafaee, A., & Saljooghi, F. (2010). Cost efficiency measures in data envelopment analysis with data uncertainty. European Journal of Operational Research, 202(2), 595–603.

    Article  Google Scholar 

  • Mozaffari, M., Kamyab, P., Jablonsky, J., & Gerami, J. (2014). Cost and revenue efficiency in DEA-R models. Computers and Industrial Engineering, 78, 188–194.

    Article  Google Scholar 

  • Mukherjee, A., Nath, P., & Pal, M. (2003). Resource, service quality and performance triad: A framework for measuring efficiency of banking services. Journal of the Operational Research Society, 54(7), 723–735.

    Article  Google Scholar 

  • Nemoto, J., & Goto, M. (1999). Dynamic data envelopment analysis: Modeling intertemporal behavior of a firm in the presence of productive inefficiencies. Economics Letters, 64(1), 51–56.

    Article  Google Scholar 

  • Nemoto, J., & Goto, M. (2003). Measurement of dynamic efficiency in production: An application of data envelopment analysis to japanese electric utilities. Journal of Productivity Analysis, 19(2–3), 191–210.

    Article  Google Scholar 

  • Puig-Junoy, J. (2000). Partitioning input cost efficiency into its allocative and technical components: An empirical dea application to hospitals. Socio-Economic Planning Sciences, 34, 199–218.

    Article  Google Scholar 

  • Ray, S. C., & Kim, H. J. (1995). Cost efficiency in the US steel industry: A nonparametric analysis using data envelopment analysis. European Journal of Operational Research, 80, 654–671.

    Article  Google Scholar 

  • Sahoo, B. K., Mehdiloozad, M., & Tone, K. (2014). Cost, revenue and profit efficiency measurement in DEA: A directional distance function approach. European Journal of Operational Research, 237(3), 921–931.

    Article  Google Scholar 

  • Sengupta, J. (1996). Dynamics of data envelopment analysis: Theory of systems efficiency. Journal of the Operational Research Society, 47(11), 1421.

    Article  Google Scholar 

  • Soleimani-damaneh, M. (2013). Another approach for estimating RTS in dynamic DEA. Journal of Productivity Analysis, 39(1), 75–81.

    Article  Google Scholar 

  • Soleimani-Damaneh, M. (2013). An enumerative algorithm for solving nonconvex dynamic DEA models. Optimization Letters, 7(1), 101–115.

    Article  Google Scholar 

  • Sueyoshi, T., & Sekitani, K. (2005). Returns to scale in dynamic DEA. European Journal of Operational Research, 161(2), 536–544.

    Article  Google Scholar 

  • Toloo, M. (2016). A cost efficiency approach for strategic vendor selection problem under certain input prices assumption. Measurement, 85, 175–183.

    Article  Google Scholar 

  • Tone, K. (2002). A strange case of the cost and allocative efficiencies in DEA. Journal of the Operational Research Society, 53(11), 1225–1231.

    Article  Google Scholar 

  • Tone, K., & Tsutsui, M. (2010). Dynamic DEA: A slacks-based measure approach. Omega, 38(3–4), 145–156.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Najafabad Branch, Islamic Azad university, Najafabad, Iran

    Khosro Soleimani-Chamkhorami

  2. Department of Mathematics, Khomeinishar Branch, Islamic Azad University, Khomeinishahr, Iran

    Saeid Ghobadi

Authors
  1. Khosro Soleimani-Chamkhorami
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Saeid Ghobadi
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Khosro Soleimani-Chamkhorami.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Soleimani-Chamkhorami, K., Ghobadi, S. Cost-efficiency under inter-temporal dependence. Ann Oper Res 302, 289–312 (2021). https://doi.org/10.1007/s10479-021-03989-2

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10479-021-03989-2

Keywords