Optimization model of trade credit and asset-based securitization financing in carbon emission reduction supply chain

Abstract

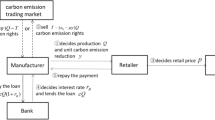
As low-carbon products increasingly become popular among consumers, the manufacturers have begun to advocate low-carbon supply chain to meet consumers’ low-carbon preferences. However, low-carbon investments inevitably bring financing constraints to the supply chain. To provide a potential solution to relieve the financial constrain, we established a two-echelon supply chain consisting of a low-carbon product manufacturer and a retailer. Supply chain members can effectively solve their financing constraints by utilizing portfolio financing consisting of the bank loan (BL), trade credit (TC), and asset-based securitization (ABS). We found that under the financial mode of BL and DC (Dual credit refers to the combination of bank loan and trade credit), only when consumers are highly price-sensitive to low-carbon products can tax preference incentivize the manufacturer to reduce carbon emissions. Under DC mode, consumer’s strong low-carbon preference will push up the retail price level of low-cost products; Under portfolio financing with ABS & DC, consumers’ strong low-carbon preference will force up the retail price level of low-carbon products with low price sensitivity. Compared with pure BL and DC, the cash flow under portfolio financing is the tightest. Besides, we took capital demand of the multi-stage scenario into consideration. Moreover, we found that the tax rate and tax deduction ratio of carbon emissions reduction will affect the retail price, wholesale price, and financing decision in the three financial modes when satisfying certain conditions.

Appendices

Appendices

1.1 Appendix 1

The optimization problem of supply chain participants under the financing model BL is

$$ \max S_{M} = \left( {w - c} \right)q - \frac{1}{2}kL^{2} - \max \left( {t_{M} ,0} \right)t + S_{M0}^{N} , $$

(A1.1)

$$ {\text{s.t.}}\quad \max S_{R} = \left( {p - w} \right)q - \max \left( {t_{R} ,0} \right)t - s\left( {1 + r} \right) + S_{R}^{0} , $$

(A1.2)

$$ wq \le S_{R}^{0} + s, $$

(A1.3)

$$ cq \le S_{M0}^{N} + s. $$

(A1.4)

where $q = A - \alpha p + \beta L$, $t_{M} = \left( {w - c} \right)q - \frac{1}{2}\delta kL^{2}$, ${ }t_{R} = \left( {p - w} \right)q - sr$.

We can reorganize and get the following results.

$$ \mathop {{\text{max}}}\limits_{{t_{M} > 0}} S_{M} = \left( {w - c} \right)\left( {A - \alpha p + \beta L} \right) - \frac{1}{2}kL^{2} - \left( {\left( {w - c} \right)q - \frac{1}{2}\delta kL^{2} } \right)t + S_{{{\text{M}}0}}^{N} $$

(A1.5)

$$ {\text{s.t.}}\quad \mathop {\max }\limits_{{t_{R} > 0}} S_{R} = \left( {p - w} \right)\left( {A - p\alpha + \beta L} \right) - \left( {\left( {p - w} \right)\left( {A - p\alpha + \beta L} \right) - sr} \right)t - s\left( {1 + r} \right) + S_{R}^{0} $$

(A1.6)

According to the idea of reverse solving, we first optimize the retailer’s problem. The first derivative and the second derivative of the retailer’s profit with respect to the decision variables are as follows.

$$ \frac{{\partial S_{R} }}{\partial p} = \left( {1 - t} \right)\left( {A - 2\alpha p + \alpha w + L\beta } \right) $$

(A1.7)

$$ \frac{{\partial^{2} S_{R} }}{{\partial p^{2} }} = - 2\left( {1 - t} \right)\alpha < 0 $$

(A1.8)

Obviously, the retailer’s profit is a concave function of $p$, and let the first derivative equal to 0, we can get the reaction function, $p = \frac{A + \alpha w + L\beta }{{2\alpha }}.$

We put the expression of $w$ into ${ }\mathop {{\text{max}}}\limits_{{t_{M} > 0}} S_{M}$, then we have the following expression.

$$ \mathop {\max }\limits_{{t_{M} > 0}} S_{M} = \left( {\frac{ - A + 2p\alpha - L\beta }{\alpha } - c} \right)\left( {A - p\alpha + \beta L} \right) - \frac{1}{2}kL^{2} - \left[ {\left( {\frac{ - A + 2p\alpha - L\beta }{\alpha } - c} \right)\left( {A - p\alpha + \beta L} \right) - \frac{1}{2}\delta kL^{2} } \right]t + S_{M0}^{N} $$

(A1.9)

The first derivative functions of the manufacturer’s profit function with respect to the decision variables are as follows.

$$ \frac{{\partial S_{M} }}{\partial w} = \frac{1}{2}\left( {1 - t} \right)(A + c\alpha - 2w\alpha + L\beta $$

(A1.10)

$$ \frac{{\partial S_{M} }}{\partial L} = \frac{1}{2}\left( {1 - t} \right)\left( {w - c} \right)\beta - kL\left( {1 - t\delta } \right) $$

(A1.11)

The Hessian matrix of the manufacturer’s profit function on the decision variables is

$$ \left| {\begin{array}{*{20}c} {\frac{{\partial^{2} S_{M} }}{{\partial w^{2} }},} & {\frac{{\partial^{2} S_{M} }}{\partial w\partial L}} \\ {\frac{{\partial^{2} S_{M} }}{\partial L\partial w},} & {\frac{{\partial^{2} S_{M} }}{{\partial L^{2} }}} \\ \end{array} } \right| = \left| {\begin{array}{*{20}c} { - \left( {1 - t} \right)\alpha ,} & {\frac{1}{2}\left( {1 - t} \right)\beta } \\ {\frac{1}{2}\left( {1 - t} \right)\beta ,} & { - k\left( {1 - t\delta } \right)} \\ \end{array} } \right| = \left( {1 - t\delta } \right)\left( {1 - t} \right)\alpha k - \frac{1}{4}\left( {1 - t} \right)^{2} \beta^{2} $$

(A1.12)

Because $\left| { - 4\left( {1 - t} \right)\alpha } \right| < 0$, the above matrix is a negative definite matrix if $\alpha > \frac{{\left( {1 - t} \right)\beta^{2} }}{{4k\left( {1 - t\delta } \right)}}$, $S_{M}$ is a joint concave function with respect to $w$ and $L$, then we have Theorem 2.

The objective function is a joint concave function, we rewrite the objective function to $\min - S_{M} = - (w - c)(A - p\alpha + \beta L) + \tfrac{1}{2}kL^{2} + ((w - c)q - \tfrac{1}{2}\delta kL^{2} )t - S_{M0}$.

It is equivalent to that the objective function is a joint concave function, and the inequality constraint function $g_{1} = cq - S_{M0} + S_{R}^{0} + s$ is a linear function, and ${ }g_{2} = S_{R}^{0} - wq$ is a convex function. Therefore, the Kuhn Tucker condition is necessary and sufficient, the local maximum is the global maximum.

Construct the Lagrangian function as follows.

$$ {\mathcal{L}}\left( {w,L,\lambda_{1} ,\lambda_{2} } \right) = \left( {w - c} \right)\left( {A - \alpha \cdot \frac{A + w\alpha + L\beta }{{2\alpha }} + \beta L} \right) - \frac{1}{2}kL^{2} - \left( {\left( {w - c} \right)q - \frac{1}{2}\delta kL^{2} } \right) \cdot t + S_{M0} - \lambda_{1} \left( {cq - S_{M0} + S_{R}^{0} + s} \right) - \lambda_{2} \left( {S_{R}^{0} - wq} \right) $$

(A1.13)

KKT conditions need to be satisfied aiming for the optimal solution, which are as follow.

$$ \left\{ {\begin{array}{*{20}l} {\frac{{\partial {\mathcal{L}}}}{\partial w} = 0} \hfill \\ {\frac{{\partial {\mathcal{L}}}}{\partial L} = 0} \hfill \\ {\lambda_{j} \ge 0,\quad j = 1,2} \hfill \\ {g_{j} \left( {w,L} \right) \le 0,\quad j = 1,2} \hfill \\ {\lambda_{j} g_{j} \left( {w,L} \right) = 0,\quad j = 1,2} \hfill \\ \end{array} } \right. $$

(A1.14)

(1) $\lambda_{1} = \lambda_{2} = 0$, In this case, the two constraints are relaxation conditions, the above conditions can be further simplified.

$$ \left\{ {\begin{array}{*{20}l} {\frac{{\partial {\mathcal{L}}}}{\partial w} = A - \frac{A + w\alpha + L\beta }{2} + L\beta - \left( {w - c} \right)\frac{\alpha }{2} - t\cdot\left( {q - \left( {w - c} \right)\cdot\alpha } \right) = 0} \hfill \\ {\frac{{\partial {\mathcal{L}}}}{\partial L} = \left( {w - c} \right)\left( {\frac{\beta }{2}} \right) - kL - t\left( {\left( {w - c} \right)\beta - \delta KL} \right) = 0} \hfill \\ \end{array} } \right. $$

(A1.15)

The solution to satisfy the equation is $L = \frac{{\beta \left( {1 - t} \right)\left( {A - \alpha c} \right)}}{{4\alpha k\left( {1 - t\delta } \right) - \beta^{2} \left( {1 - t} \right)}}$, $w = \frac{{2k\left( {1 - \delta t} \right)\left( {A + \alpha c} \right) - c\beta^{2} \left( {1 - t} \right)}}{{4\alpha k\left( {1 - t\delta } \right) - \beta^{2} \left( {1 - t} \right)}}$.

Next, we need to verify the result.

First, verification of $g_{1} \left( {w,L} \right) < 0$. From previous results, we have $\left\{ {\begin{array}{*{20}l} {\beta L - \alpha w > \frac{2\alpha sr}{q} - A} \hfill \\ {\left( {w - c} \right)q - \frac{1}{2}\delta kL^{2} > 0} \hfill \\ {pq > wq - S_{R}^{0} } \hfill \\ \end{array} } \right. \Leftrightarrow \left\{ {\begin{array}{*{20}l} {q^{2} > 2\alpha sr} \hfill \\ {\left( {w - c} \right)\left( {A + \beta L - \alpha w} \right) - \frac{1}{2}\delta kL^{2} > 0} \hfill \\ {S_{R}^{0} > wq - pq} \hfill \\ \end{array} } \right. \Leftrightarrow wq - \frac{1}{2}\delta kL^{2} > cq$, $A + \beta L - \alpha w = q > \sqrt {2\alpha sr} \Leftrightarrow \frac{{A + \beta L - \sqrt {2\alpha sr} }}{\alpha } > w$, and $\sqrt {2\alpha sr} < q = A + \beta L - \alpha w\left\langle {A + \beta L \Leftrightarrow L} \right\rangle \frac{{\sqrt {2\alpha sr} - A}}{\beta }$. Therefore $g_{1} \left( {w,L} \right) = cq - S_{M0} + S_{R}^{0} + s < wq - \frac{1}{2}\delta kL^{2} - S_{M0} + S_{R}^{0} + s < \frac{{A + \beta L - \sqrt {2\alpha sr} }}{\alpha } \cdot q - \frac{1}{2}\delta kL^{2} - S_{M0} + S_{R}^{0} + s = \frac{{A\left( {A - \sqrt {2\alpha sr} } \right) + \frac{{\beta^{2} \left( {1 - 2t} \right)\left( {A - c\alpha } \right)\left( {2A - \sqrt {2\alpha sr} } \right)}}{{4\alpha k\left( {1 - t\delta } \right) - \beta^{2} \left( {1 - 2t} \right)}}}}{\alpha } + \left( {\frac{{\beta^{2} }}{\alpha } - \frac{\delta k}{2}} \right)\left( {\frac{{\beta \left( {1 - 2t} \right)\left( {A - c\alpha } \right)}}{{4\alpha k\left( {1 - t\delta } \right) - \beta^{2} \left( {1 - 2t} \right)}}} \right)^{2} - S_{M0} + S_{R}^{0} + s$. When $\frac{{A\left( {A - \sqrt {2\alpha sr} } \right) + \frac{{\beta^{2} \left( {1 - 2t} \right)\left( {A - c\alpha } \right)\left( {2A - \sqrt {2\alpha sr} } \right)}}{{4\alpha k\left( {1 - t\delta } \right) - \beta^{2} \left( {1 - 2t} \right)}}}}{\alpha } + \left( {\frac{{\beta^{2} }}{\alpha } - \frac{\delta k}{2}} \right)\left( {\frac{{\beta \left( {1 - 2t} \right)\left( {A - c\alpha } \right)}}{{4\alpha k\left( {1 - t\delta } \right) - \beta^{2} \left( {1 - 2t} \right)}}} \right)^{2} + S_{R}^{0} + s < S_{M0}$, $g_{1} \left( {w,L} \right) < 0$ holds, but its establishing is under some condition.

Second, verification of $g_{2} \left( {w,L} \right) < 0$. $g_{2} \left( {w,L} \right) = S_{R}^{0} - wq < S_{R}^{0} - \left( {cq + \frac{1}{2}\delta kL^{2} } \right) < S_{R}^{0} - \left( {c\sqrt {2\alpha sr} + \frac{1}{2}\delta kL^{2} } \right) = S_{R}^{0} - \left( {c\sqrt {2\alpha sr} + \frac{\delta k}{2}\left( {\frac{{\beta \left( {1 - 2t} \right)\left( {A - c\alpha } \right)}}{{4\alpha k\left( {1 - t\delta } \right) - \beta^{2} \left( {1 - 2t} \right)}}} \right)^{2} } \right)$. When $S_{R}^{0} < \sqrt {2\alpha sr} + \frac{\delta k}{2}\left( {\frac{{\beta \left( {1 - 2t} \right)\left( {A - c\alpha } \right)}}{{4\alpha k\left( {1 - t\delta } \right) - \beta^{2} \left( {1 - 2t} \right)}}} \right)^{2}$, $g_{2} \left( {w,L} \right) < 0$ holds, but its establishing is under some condition.

To sum up, when the parameters meet both $g_{1} \left( {w,L} \right) < 0$ and $g_{2} \left( {w,L} \right) < 0$ at the same time, that is, $S_{R}^{0} < {\text{min}}\left( {S_{M0} - s - \frac{{A\left( {A - \sqrt {2\alpha sr} } \right) + \frac{{\beta^{2} \left( {1 - 2t} \right)\left( {A - c\alpha } \right)\left( {2A - \sqrt {2\alpha sr} } \right)}}{{4\alpha k\left( {1 - t\delta } \right) - \beta^{2} \left( {1 - 2t} \right)}}}}{\alpha } + \left( {\frac{{\beta^{2} }}{\alpha } - \frac{\delta k}{2}} \right)\left( {\frac{{\beta \left( {1 - 2t} \right)\left( {A - c\alpha } \right)}}{{4\alpha k\left( {1 - t\delta } \right) - \beta^{2} \left( {1 - 2t} \right)}}} \right)^{2} ,\sqrt {2\alpha sr} + \frac{\delta k}{2}\left( {\frac{{\beta \left( {1 - 2t} \right)\left( {A - c\alpha } \right)}}{{4\alpha k\left( {1 - t\delta } \right) - \beta^{2} \left( {1 - 2t} \right)}}} \right)^{2} } \right)$, which implies if the working capital of retailer is lower than a certain threshold, there is an optimal feasible solution 1.

After $w$ and $L$ are determined, according to the retailer’s response function $p = \frac{A + \alpha w + L\beta }{{2\alpha }}$, we can get the product price, and finally get the following result.

$$ \left\{ {\begin{array}{*{20}l} {p^{*} = \frac{{k\left( {1 - t\delta } \right)\left( {3A + \alpha c} \right) - c\beta^{2} \left( {1 - t} \right)}}{{4\alpha k\left( {1 - t\delta } \right) - \beta^{2} \left( {1 - t} \right)}}} \hfill \\ {L^{*} = \frac{{\beta \left( {1 - t} \right)\left( {A - \alpha c} \right)}}{{4\alpha k\left( {1 - t\delta } \right) - \beta^{2} \left( {1 - t} \right)}}} \hfill \\ {w^{*} = \frac{{2k\left( {1 - t\delta } \right)\left( {A + \alpha c} \right) - c\beta^{2} \left( {1 - t} \right)}}{{4\alpha k\left( {1 - t\delta } \right) - \beta^{2} \left( {1 - t} \right)}}} \hfill \\ \end{array} } \right. $$

(A1.16)

(2) $\lambda_{1} > 0,\lambda_{2} = 0$.

In this case, one of the constraints is relaxation condition, the KKT conditions are as follow.

$$ \left\{ {\begin{array}{*{20}l} {\frac{{\partial {\mathcal{L}}}}{\partial w} = A - \frac{A + w\alpha + L\beta }{2} + L\beta - \left( {w - c} \right)\frac{\alpha }{2} - t \cdot \left( {q - \left( {w - c} \right) \cdot \alpha } \right) + \lambda_{1} c\alpha = 0} \hfill \\ {\frac{{\partial {\mathcal{L}}}}{\partial L} = \left( {w - c} \right)\left( {\frac{\beta }{2}} \right) - kL - t\left( {\left( {w - c} \right)\beta - \delta KL} \right) - \lambda_{1} \beta = 0} \hfill \\ {\frac{{\partial {\mathcal{L}}}}{{\partial \lambda_{1} }} = cq - S_{M0} + S_{R}^{0} + s = 0} \hfill \\ \end{array} } \right. $$

(A1.17)

Verification of $g_{2} \left( {w,L} \right) \le 0$, where $g_{2} \left( {w,L} \right) = S_{R}^{0} - wq = S_{R}^{0} - \left( {\frac{A}{\alpha } + \frac{{S_{M0} + S_{R}^{0} + s}}{c\alpha } \cdot \left( {\frac{{\beta^{2} \left( {1 - 2t} \right)}}{{2k\left( {1 - t\delta } \right) \cdot \alpha }} - 1} \right)} \right) \cdot \frac{{S_{M0} + S_{R}^{0} + s}}{c}$.When the retailer’s working capital meet condition: $S_{R}^{0} \le \left( {\frac{A}{\alpha } + \frac{{S_{M0} + S_{R}^{0} + s}}{c\alpha } \cdot \left( {\frac{{\beta^{2} \left( {1 - 2t} \right)}}{{2k\left( {1 - t\delta } \right)\cdot\alpha }} - 1} \right)} \right) \cdot \frac{{S_{M0} + S_{R}^{0} + s}}{c}$, $g_{2} \left( {w,L} \right) \le 0$ holds and there is an optimal feasible solution 2.

$$ \left\{ {\begin{array}{*{20}l} {w = \frac{A}{\alpha } + \frac{{S_{M0} + S_{R}^{0} + s}}{c\alpha } \cdot \left( {\frac{{\beta^{2} \left( {1 - 2t} \right)}}{{2k\left( {1 - t\delta } \right)\cdot\alpha }} - 1} \right)} \hfill \\ {L = \frac{{S_{M0} + S_{R}^{0} + s}}{c\alpha } \cdot \frac{{\beta \left( {1 - 2t} \right)}}{{2k\left( {1 - t\delta } \right)}}} \hfill \\ {\lambda_{1} = \left( {\frac{A}{c\alpha } + \frac{{S_{M0} + S_{R}^{0} + s}}{{c^{2} \alpha }} \cdot \left( {\frac{{\beta^{2} \left( {1 - 2t} \right)}}{{2k\left( {1 - t\delta } \right)\cdot\alpha }} - 2} \right) - 1} \right)\left( {1 - 2t} \right)} \hfill \\ \end{array} } \right. $$

(A1.18)

The product price decision is the same as in scenario (1).

(3) $\lambda_{1} = 0,\lambda_{2} > 0$.

In this case, one of the constraints is relaxation condition, the KKT conditions are as follow.

$$ \left\{ {\begin{array}{*{20}l} {\frac{{\partial {\mathcal{L}}}}{\partial w} = A - \frac{A + w\alpha + L\beta }{2} + L\beta - \left( {w - c} \right)\frac{\alpha }{2} - t \cdot \left( {q - \left( {w - c} \right)\cdot\alpha } \right) - \lambda_{2} \left( { - q + w\alpha } \right) = 0} \hfill \\ {\frac{{\partial {\mathcal{L}}}}{\partial L} = \left( {w - c} \right)\frac{\beta }{2} - kL - t\left( {\left( {w - c} \right)\beta - \delta KL} \right) + \lambda_{2} w\beta = 0} \hfill \\ {\frac{{\partial {\mathcal{L}}}}{{\partial \lambda_{2} }} = S_{R}^{0} - wq = 0} \hfill \\ \end{array} } \right. $$

(A1.19)

$\lambda_{2}$ is the solution of (A1.20).

$$ \left( {1 - 2t - \lambda_{2} } \right)\beta \cdot \left( {\frac{{c\left( {1 - 2t} \right)}}{{2\lambda_{2} }} + \sqrt {\left( {\frac{{c\left( {1 - 2t} \right)}}{{2\lambda_{2} }}} \right)^{2} - \frac{{S_{R}^{0} }}{\alpha }} } \right) = c\beta \left( {1 - 2t} \right) + \frac{{2k\left( {1 - t\delta } \right)}}{\beta } \cdot \left( {\frac{{S_{R}^{0} }}{{\frac{{c\left( {1 - 2t} \right)}}{{2\lambda_{2} }} + \sqrt {\left( {\frac{{c\left( {1 - 2t} \right)}}{{2\lambda_{2} }}} \right)^{2} - \frac{{S_{R}^{0} }}{\alpha }} }} + \alpha \left( {\frac{{c\left( {1 - 2t} \right)}}{{2\lambda_{2} }} + \sqrt {\left( {\frac{{c\left( {1 - 2t} \right)}}{{2\lambda_{2} }}} \right)^{2} - \frac{{S_{R}^{0} }}{\alpha }} } \right) - A} \right) $$

(A1.20)

So the optimal solution is $\left\{ {\begin{array}{*{20}l} {\lambda_{2}^{*} } \hfill \\ {w = \frac{{c\left( {1 - 2t} \right)}}{{2\lambda_{2} }} + \sqrt {\left( {\frac{{c\left( {1 - 2t} \right)}}{{2\lambda_{2} }}} \right)^{2} - \frac{{S_{R}^{0} }}{\alpha }} } \hfill \\ {L = \frac{1}{\beta } \cdot \left( {\frac{{S_{R}^{0} }}{{\frac{{c\left( {1 - 2t} \right)}}{{2\lambda_{2} }} + \sqrt {\left( {\frac{{c\left( {1 - 2t} \right)}}{{2\lambda_{2} }}} \right)^{2} - \frac{{S_{R}^{0} }}{\alpha }} }} + \alpha \cdot \left( {\frac{{c\left( {1 - 2t} \right)}}{{2\lambda_{2} }} + \sqrt {\left( {\frac{{c\left( {1 - 2t} \right)}}{{2\lambda_{2} }}} \right)^{2} - \frac{{S_{R}^{0} }}{\alpha }} } \right) - A} \right)} \hfill \\ \end{array} } \right.$.

Verification of $g_{1} \left( {w,L} \right) \le 0$, where $g_{1} \left( {w,L} \right) = cq - S_{M0} + S_{R}^{0} + s < wq - \frac{1}{2}\delta kL^{2} - S_{M0} + S_{R}^{0} + s < \frac{{\left( {A + \beta L} \right)^{2} - \left( {A + \beta L} \right) \cdot \sqrt {2\alpha sr} }}{\alpha } - \frac{1}{2}\delta kL^{2} - S_{M0} + S_{R}^{0} + s = \frac{A}{\alpha }\left( {A - \sqrt {2\alpha sr} } \right) + \frac{{\frac{{\left( {2A - \sqrt {2\alpha sr} } \right)}}{\alpha } \cdot S_{R}^{0} }}{{\frac{{c\left( {1 - 2t} \right)}}{{2\lambda_{2} }} + \sqrt {\left( {\frac{{c\left( {1 - 2t} \right)}}{{2\lambda_{2} }}} \right)^{2} - \frac{{S_{R}^{0} }}{\alpha }} }} + \frac{{c\left( {1 - 2t} \right)}}{{2\lambda_{2} }} + \sqrt {\left( {\frac{{c\left( {1 - 2t} \right)}}{{2\lambda_{2} }}} \right)^{2} - \frac{{S_{R}^{0} }}{\alpha }} - A + \left( {1 - \frac{\alpha \delta k}{{2\beta^{2} }}} \right) \cdot \left[ {\frac{{S_{R}^{0} }}{{\frac{{c\left( {1 - 2t} \right)}}{{2\lambda_{2} }} + \sqrt {\left( {\frac{{c\left( {1 - 2t} \right)}}{{2\lambda_{2} }}} \right)^{2} - \frac{{S_{R}^{0} }}{\alpha }} }} + \alpha \cdot \left( {\frac{{c\left( {1 - 2t} \right)}}{{2\lambda_{2} }} + \sqrt {\left( {\frac{{c\left( {1 - 2t} \right)}}{{2\lambda_{2} }}} \right)^{2} - \frac{{S_{R}^{0} }}{\alpha }} } \right) - A} \right]^{2} - S_{M0} + S_{R}^{0} + s$. When the manufacturer’s working capital meet condition $\frac{A}{\alpha }\left( {A - \sqrt {2\alpha sr} } \right) + \frac{{\frac{{\left( {2A - \sqrt {2\alpha sr} } \right)}}{\alpha } \cdot S_{R}^{0} }}{{\frac{{c\left( {1 - 2t} \right)}}{{2\lambda_{2} }} + \sqrt {\left( {\frac{{c\left( {1 - 2t} \right)}}{{2\lambda_{2} }}} \right)^{2} - \frac{{S_{R}^{0} }}{\alpha }} }} + \frac{{c\left( {1 - 2t} \right)}}{{2\lambda_{2} }} + \sqrt {\left( {\frac{{c\left( {1 - 2t} \right)}}{{2\lambda_{2} }}} \right)^{2} - \frac{{S_{R}^{0} }}{\alpha }} - A + \left( {1 - \frac{\alpha \delta k}{{2\beta^{2} }}} \right) \cdot \left[ {\frac{{S_{R}^{0} }}{{\frac{{c\left( {1 - 2t} \right)}}{{2\lambda_{2} }} + \sqrt {\left( {\frac{{c\left( {1 - 2t} \right)}}{{2\lambda_{2} }}} \right)^{2} - \frac{{S_{R}^{0} }}{\alpha }} }} + \alpha \cdot \left( {\frac{{c\left( {1 - 2t} \right)}}{{2\lambda_{2} }} + \sqrt {\left( {\frac{{c\left( {1 - 2t} \right)}}{{2\lambda_{2} }}} \right)^{2} - \frac{{S_{R}^{0} }}{\alpha }} } \right) - A} \right]^{2} + S_{R}^{0} + s < S_{M0}$, there is an optimal feasible solution 3.

The product price decision is the same as in scenario (1).

(4) $\lambda_{1} > 0,\lambda_{2} > 0$, the KKT conditions are as follow.

$$ \left\{ {\begin{array}{*{20}l} {\frac{{\partial {\mathcal{L}}}}{\partial w} = A - \frac{A + w\alpha + L\beta }{2} + L\beta - \left( {w - c} \right)\frac{\alpha }{2} - t\cdot\left( {q - \left( {w - c} \right)\cdot\alpha } \right) + \lambda_{1} c\alpha - \lambda_{2} \left( { - q + w\alpha } \right) = 0} \hfill \\ {\frac{{\partial {\mathcal{L}}}}{\partial L} = \left( {w - c} \right)\frac{\beta }{2} - kL - t\left( {\left( {w - c} \right)\beta - \delta KL} \right) - \lambda_{1} c\beta + \lambda_{2} w\beta = 0} \hfill \\ {\frac{{\partial {\mathcal{L}}}}{{\partial \lambda_{1} }} = g_{1} \left( {w,L} \right) = cq - S_{M0} + S_{R}^{0} + s = 0} \hfill \\ {\frac{{\partial {\mathcal{L}}}}{{\partial \lambda_{2} }} = g_{2} \left( {w,L} \right) = S_{R}^{0} - wq = 0} \hfill \\ \end{array} } \right. $$

(A1.21)

When the parameters meet (A1.22), there is an optimal feasible solution 4, which is expressed in (A1.23).

$$ \left\{ {\begin{array}{*{20}l} {\frac{{2k\alpha \left( {1 - t\delta } \right)}}{\beta } \cdot \left( {\frac{1}{\beta } + \frac{{\frac{{c\alpha S_{R}^{0} }}{{S_{M0} - S_{R}^{0} - s}} - A}}{{\beta \left( {\frac{{S_{M0} - S_{R}^{0} - s}}{c}} \right)}} \cdot } \right) + 2t > 1} \hfill \\ {\frac{1}{c\alpha }\left( {w\alpha - \frac{{S_{M0} - S_{R}^{0} - s}}{c}} \right) \cdot \left( {\frac{{2k\alpha \left( {1 - t\delta } \right)}}{\beta } \cdot \left( {\frac{1}{\beta } + \frac{{\frac{{c\alpha S_{R}^{0} }}{{S_{M0} - S_{R}^{0} - s}} - A}}{{\beta \left( {\frac{{S_{M0} - S_{R}^{0} - s}}{c}} \right)}} \cdot } \right) - 1 + 2t} \right) > \left( {c\alpha - w\alpha + \frac{{S_{M0} - S_{R}^{0} - s}}{c}} \right) \cdot \frac{{\left( {1 - 2t} \right)}}{c\alpha }} \hfill \\ \end{array} } \right. $$

(A1.22)

$$ \left\{ {\begin{array}{*{20}l} {w = \frac{{cS_{R}^{0} }}{{S_{M0} - S_{R}^{0} - s}}} \hfill \\ {L = \frac{1}{\beta } \cdot \left( {\frac{{S_{M0} - S_{R}^{0} - s}}{c} + \frac{{c\alpha S_{R}^{0} }}{{S_{M0} - S_{R}^{0} - s}} - A} \right)} \hfill \\ {\lambda_{1} = \frac{1}{c\alpha }\left( {w\alpha - \frac{{S_{M0} - S_{R}^{0} - s}}{c}} \right) \cdot \left( {\frac{{2k\alpha \left( {1 - t\delta } \right)}}{\beta } \cdot \left( {\frac{1}{\beta } + \frac{{\frac{{c\alpha S_{R}^{0} }}{{S_{M0} - S_{R}^{0} - s}} - A}}{{\beta \left( {\frac{{S_{M0} - S_{R}^{0} - s}}{c}} \right)}} \cdot } \right) - 1 + 2t} \right) - \left( {c\alpha - w\alpha + \frac{{S_{M0} - S_{R}^{0} - s}}{c}} \right) \cdot \frac{{\left( {1 - 2t} \right)}}{c\alpha }} \hfill \\ {\lambda_{2} = \frac{{2k\alpha \left( {1 - t\delta } \right)}}{\beta } \cdot \left( {\frac{1}{\beta } + \frac{{\frac{{c\alpha S_{R}^{0} }}{{S_{M0} - S_{R}^{0} - s}} - A}}{{\beta \left( {\frac{{S_{M0} - S_{R}^{0} - s}}{c}} \right)}} \cdot } \right) - 1 + 2t} \hfill \\ \end{array} } \right. $$

(A1.23)

The product price decision is the same as in scenario (1).

1.2 Appendix 2

$\frac{{\partial p^{*} }}{\partial t} = \frac{{3k\left( {c\alpha - A} \right)\beta^{2} \left( {1 - \delta } \right)}}{{\left( {4k\alpha \left( {1 - t\delta } \right) - \left( {1 - t} \right)\beta^{2} } \right)^{2} }}$. Obviously, the sign of $\frac{{\partial p^{*} }}{\partial t}$ is the same as the numerator. Because $0 \le \delta \le 1$, there is $\frac{{\partial p^{*} }}{\partial t} > 0$ if $\alpha > \frac{A}{c}$, then $p^{*}$ increases in $t$; if $\alpha < \frac{{\text{A}}}{c}$, we have $\frac{{\partial p^{*} }}{\partial t} < 0$, then $p^{*}$ decreases in $t$.

1.3 Appendix 3

$$ \frac{{\partial p^{*} }}{\partial \delta } = \frac{{3k\left( {1 - t} \right)t\left( {A - c\alpha } \right)\beta^{2} }}{{\left( {4k\alpha \left( {1 - t\delta } \right) - \left( {1 - t} \right)\beta^{2} } \right)^{2} }} $$

(A3.1)

Similarly, because $0 \le \delta \le 1$, there is $\frac{{\partial p^{*} }}{\partial \delta } < 0$ if $\alpha > \frac{A}{c}$, then $p^{*}$ decreases in $\delta$; if $\alpha < \frac{A}{c}$, we have $\frac{{\partial p^{*} }}{\partial \delta } > 0$, then $p^{*}$ increases in $\delta$.

1.4 Appendix 4

$\frac{{\partial p^{*} }}{\partial \beta } = \frac{{6k\beta \left( {1 - t\delta } \right)\left( {1 - t} \right)}}{{\left( {4k\alpha \left( {1 - t\delta } \right) - \left( {1 - t} \right)\beta^{2} } \right)^{2} }}\left( {A - c\alpha } \right)$, the denominator must be greater than zero. According to the meaning of $t$, $\delta$, $k$, $\beta$, the sign is positive for $1 - t\delta$, $1 - t$, $k$, $\beta$. This implies the sign for $\frac{{\partial p^{*} }}{\partial \beta }$ is dependent on $A - c\alpha$. When $A - c\alpha > 0$, that is $\alpha < \frac{A}{c}$, we have $\frac{{\partial p^{*} }}{\partial \beta } > 0$, then $p^{*}$ increases in $\beta$. When $A - c\alpha < 0$, that is $\alpha > \frac{A}{c}$, we can get $\frac{{\partial p^{*} }}{\partial \beta } < 0$, then $p^{*}$ decreases in $\beta$.

1.5 Appendix 5

$$ \frac{{\partial w^{*} }}{\partial t} = - \frac{{2k\left( {A - c\alpha } \right)\beta^{2} \left( {1 - \delta } \right)}}{{\left( {4k\alpha \left( {1 - t\delta } \right) - \left( {1 - t} \right)\beta^{2} } \right)^{2} }} $$

(A5.1)

$$ \frac{{\partial w^{*} }}{\partial \delta } = \frac{{2k\left( {1 - t} \right)t\left( {A - c\alpha } \right)\beta^{2} }}{{\left( {4k\alpha \left( {1 - t\delta } \right) - \left( {1 - t} \right)\beta^{2} } \right)^{2} }} $$

(A5.2)

Obviously, the denominator of the two equations is positive. Because $0 \le \delta \le 1$, $0 \le t \le 1$, the sign of $\frac{{\partial w^{*} }}{\partial t}$ is opposite to that of $A - c\alpha$, while the sign of $\frac{{\partial w^{*} }}{\partial \delta }$ is the same as that of $A - c\alpha$. Thus, there are $\frac{{\partial w^{*} }}{\partial t} > 0$ and $\frac{{\partial w^{*} }}{\partial \delta } < 0$ if $\alpha > \frac{A}{c}$; if $\alpha < \frac{A}{c}$, we have $\frac{{\partial w^{*} }}{\partial t} < 0$, $\frac{{\partial w^{*} }}{\partial \delta } > 0$.

1.6 Appendix 6

$$ \frac{{\partial L^{*} }}{\partial \delta } = \frac{{4k\alpha t\left( {A - c\alpha } \right)\beta \left( {1 - t} \right)}}{{\left( {4\alpha k\left( {1 - t\delta } \right) - \left( {1 - t} \right)\beta^{2} } \right)^{2} }} $$

(A6.1)

Similarly, we have $\frac{{4k\alpha t\beta \left( {1 - t} \right)}}{{\left( {4\alpha k\left( {1 - t\delta } \right) - \left( {1 - t} \right)\beta^{2} } \right)^{2} }} > 0$. When $\alpha < \frac{A}{c}$, $\frac{{\partial L^{*} }}{\partial \delta } < 0$, then $L^{*}$ decreases in $\delta$; when $\alpha > \frac{A}{c}$, $\frac{{\partial L^{*} }}{\partial \delta } > 0$, then $L^{*}$ increases in $\delta$.

1.7 Appendix 7

The optimization problem of supply chain participants under the financing model DC is

$$ \max S_{M} = \left( {w_{\vartriangle } - c} \right)q - \max \left( {t_{M} ,0} \right)t + S_{M0} - \frac{1}{2}kL^{2} $$

(A7.1)

$$ {\text{s.t.}}\quad \max S_{R} = pq - \max \left( {t_{R} ,0} \right)t - s\left( {1 + r} \right) - \left( {w_{\Delta } q - s - S_{R}^{0} } \right) $$

(A7.2)

$$ w_{\Delta } q \ge S_{R}^{0} + s $$

(A7.3)

$$ pq - s\left( {1 + r} \right) \ge w_{\vartriangle } q - s - S_{R}^{0} $$

(A7.4)

$$ cq \le S_{{{\text{M}}0}} + s + S_{R}^{0} $$

(A7.5)

The demand function is $q = A - \alpha p + \beta L$, where $t_{M} = \left( {w_{\vartriangle } - c} \right)q - \frac{1}{2}\delta kL^{2}$, $t_{R} = \left( {p - w_{\vartriangle } } \right)q - sr$.

We can reorganize and get the following results.

$$ \mathop {\max }\limits_{{t_{M} > 0}} S_{M} = \left( {\left( {w + \Delta } \right) - c} \right)\left( {A - p\alpha + \beta L} \right) - \left( {\left( {\left( {w + \Delta } \right) - c} \right)\left( {A - p\alpha + \beta L} \right) - \frac{1}{2}\delta kL^{2} } \right)t + S_{M0} - \frac{1}{2}kL^{2} $$

(A7.6)

$$ s.t.\,\mathop {\max }\limits_{{t_{R} > 0,}} S_{R} = p\left( {A - p\alpha + \beta L} \right) - \left( {\left( {p - \left( {w + \Delta } \right)} \right)\left( {A - p\alpha + \beta L} \right) - sr} \right)t - s\left( {1 + r} \right) - \left( {\left( {A - p\alpha + \beta L} \right)\left( {w + \Delta } \right) - S} \right) + S_{R}^{0} $$

(A7.7)

According to the idea of reverse solving, we first optimize the retailer’s problem. The first derivative and the second derivative of the retailer’s profit function with respect to the decision variables are as follows.

$$ \frac{{\partial S_{R} }}{\partial p} = \left( {1 - t} \right)\left( {A - 2p\alpha + w\alpha + L\beta + \alpha \Delta } \right) $$

(A7.8)

$$ \frac{{\partial^{2} S_{R} }}{{\partial p^{2} }} = - 2\left( {1 - t} \right)\alpha < 0 $$

(A7.9)

Obviously, the retailer’s profit function is a concave function of $p$, and let the first derivative is equal to 0, we can get the reaction function, $p = \frac{A + w\alpha + L\beta + \alpha \Delta }{{2\alpha }}$.

We put the expression of w into $\mathop {\max }\limits_{{t_{M} > 0}} S_{M}$, then we have the following expression.

$$ \mathop {\max }\limits_{{t_{M} > 0}} S_{M} = \left( {\left( {\frac{ - A + 2p\alpha - L\beta - \alpha \Delta }{\alpha } + \Delta } \right) - c} \right)\left( {A - p\alpha + \beta L} \right) - \left( {\left( {\left( {\frac{ - A + 2p\alpha - L\beta - \alpha \Delta }{\alpha } + \Delta } \right) - c} \right)\left( {A - p\alpha + \beta L} \right) - \frac{1}{2}\delta kL^{2} } \right)t + S_{M0} - \frac{1}{2}kL^{2} $$

(A7.10)

The first derivative functions of the manufacturer’s profit function with respect to the decision variables are as follows.

$$ \frac{{\partial S_{M} }}{\partial w} = \left( {A - \frac{{A + w_{\Delta } \alpha + L\beta }}{2} + L\beta - \left( {w_{\Delta } - c} \right)\frac{\alpha }{2}} \right)\left( {1 - t} \right) $$

(A7.11)

$$ \frac{{\partial S_{M} }}{\partial L} = \frac{\beta }{2}\left( {w_{\Delta } - c} \right)\left( {1 - t} \right) - kL\left( {1 - \delta t} \right) = 0 $$

(A7.12)

The Hessian matrix of the manufacturer’s profit function on the decision variables is

$$ \left| {\begin{array}{*{20}c} {\frac{{\partial^{2} S_{M} }}{{\partial w^{2} }},} & {\frac{{\partial^{2} S_{M} }}{\partial w\partial L}} \\ {\frac{{\partial^{2} S_{M} }}{\partial L\partial w},} & {\frac{{\partial^{2} S_{M} }}{{\partial L^{2} }}} \\ \end{array} } \right| = \left| {\begin{array}{*{20}c} { - \left( {1 - t} \right)\alpha ,} & {\frac{\beta }{2}\left( {1 - t} \right)} \\ {\frac{\beta }{2}\left( {1 - t} \right)\beta ,} & { - k\left( {1 - t\delta } \right)} \\ \end{array} } \right| $$

(A7.13)

Because of $\left| { - \left( {1 - t} \right)\alpha } \right| < 0$, so if $\alpha > \frac{{\left( {1 - t} \right)\beta^{2} }}{{4k\left( {1 - t\delta } \right)}}$, the above matrix is a negative definite matrix, $S_{M}$ is a joint concave function with respect to $w$ and $L$, both wholesale price $w$ and carbon emission reduction level $L$ has optimal solution.

The objective function is a joint concave function and it can be revised as follow, $\min - S_{M} = - \left( {\frac{ - A + 2p\alpha - L\beta }{\alpha } - c} \right)\left( {A - p\alpha + \beta L} \right)\left( {1 - t} \right) + \frac{{kL^{2} }}{2}\left( {1 - \delta t} \right) - S_{M0}$. It is equivalent to that the objective function is a joint concave function, and the inequality constraint function $g_{1} = cq - S_{M0} + S_{R}^{0} + s$ is a linear function, and $g_{2} = S_{R}^{0} - w_{\Delta } q$ is a convex function. Therefore, the Kuhn Tucker condition is necessary and sufficient, and the local maximum is the global maximum.

Construct the Lagrangian function as follows.

$$ {\mathcal{L}}\left( {w,L,\lambda_{1} ,\lambda_{2} } \right) = \left( {w_{\Delta } - c} \right)\left( {A - p\alpha + \beta L} \right)\left( {1 - t} \right) - \frac{{kL^{2} }}{2}\left( {1 - \delta t} \right) + S_{M0} - \lambda_{1} \left( {cq - S_{M0} + S_{R}^{0} + s} \right) - \lambda_{2} \left( {s + S_{R}^{0} - w_{\Delta } q} \right) $$

(A7.14)

The KKT conditions satisfied by the optimal solution are as follows.

$$ \left\{ {\begin{array}{*{20}l} {\frac{{\partial {\mathcal{L}}}}{{\partial w_{\Delta } }} = 0} \hfill \\ {\frac{{\partial {\mathcal{L}}}}{\partial L} = 0} \hfill \\ {\lambda_{j} \ge 0,j = 1,2} \hfill \\ {g_{j} \left( {w,L} \right) \le 0,j = 1,2} \hfill \\ {\lambda_{j} g_{j} \left( {w,L} \right) = 0,j = 1,2} \hfill \\ \end{array} } \right. $$

(A7.15)

(1) $\lambda_{1} = \lambda_{2} = 0$. The above conditions can be further simplified.

$$ \left\{ {\begin{array}{*{20}l} {\frac{{\partial {\mathcal{L}}}}{{\partial w_{\Delta } }} = \left( {A - \frac{{A + w_{\Delta } \alpha + L\beta }}{2} + L\beta - \left( {w_{\Delta } - c} \right)\frac{\alpha }{2}} \right)\left( {1 - t} \right) = 0} \hfill \\ {\frac{{\partial {\mathcal{L}}}}{\partial L} = \frac{\beta }{2}\left( {w_{\Delta } - c} \right)\left( {1 - t} \right) - kL\left( {1 - \delta t} \right) = 0} \hfill \\ \end{array} } \right. $$

(A7.16)

The solution to satisfy the equation is $L^{*} = \frac{{\beta \left( {1 - t} \right)\left( {\alpha c - A} \right)}}{{\beta^{2} \left( {1 - t} \right) - 4\alpha k\left( {1 - \delta t} \right)}}$, $w^{*} = \frac{{2\alpha k\left( {1 - \delta t} \right)\left( {A + \alpha \left( {c - 2\Delta } \right)} \right) - \beta^{2} \left( {1 - t} \right)\left( {c - \Delta } \right)}}{{(\beta^{2} \left( {1 - t} \right) - 4\alpha k\left( {1 - \delta t} \right)}}$.

Verification of $g_{1} \left( {w,L} \right) < 0$. $g_{1} \left( {w_{\Delta } ,L} \right) = cq - S_{M0} + S_{R}^{0} + s \Leftrightarrow g_{1} \left( {w_{\Delta } ,L} \right) < \frac{{\left( {A + \beta L} \right)\left( {A + \beta L - \alpha w_{\Delta } } \right)}}{\alpha } - 2sr - \frac{{\delta kL^{2} }}{2} - S_{M0} + S_{R}^{0} + s$.

$= \frac{{\left( {A + \beta L} \right)\left( {A + \beta L - \frac{L\beta + \alpha c + A}{2}} \right)}}{\alpha } - 2sr - \frac{{\delta kL^{2} }}{2} - S_{M0} + S_{R}^{0} + s$, insert $L^{*}$ into the left equation, we have $g_{1} \left( {w_{\Delta } ,L} \right) < \frac{{\left( {A + \beta L} \right)\left( {A + \beta L - \alpha c} \right)}}{2\alpha } - 2sr - \frac{{\delta kL^{2} }}{2} - S_{M0} + S_{R}^{0} + s$. When $\frac{{\left( {c\beta^{2} \left( {1 - t} \right) - A4k\left( {1 - \delta t} \right)} \right)\cdot\left( {\alpha c - A} \right)4\alpha k\left( {1 - \delta t} \right)}}{{2\left( {\beta^{2} \left( {1 - t} \right) - 4\alpha k\left( {1 - \delta t} \right)} \right)^{2} }} < 2sr + S_{M0} - S_{R}^{0} - s + \frac{\delta k}{2} \cdot \left( {\frac{{\beta \left( {1 - t} \right)\left( {\alpha c - A} \right)}}{{\beta^{2} \left( {1 - t} \right) - 4\alpha k\left( {1 - \delta t} \right)}}} \right)^{2}$, $g_{1} \left( {w_{\Delta } ,L} \right) < 0$ holds.

Verification of $g_{2} \left( {w,L} \right) < 0$. $g_{2} \left( {w,L} \right) = s + S_{R}^{0} - w_{\Delta } q < s + S_{R}^{0} - c\sqrt {2\alpha sr} - \frac{\delta k}{2} \cdot \left( {\frac{{\beta \left( {1 - t} \right)\left( {\alpha c - A} \right)}}{{\beta^{2} \left( {1 - t} \right) - 4\alpha k\left( {1 - \delta t} \right)}}} \right)^{2}$, so when $s + S_{R}^{0} < c\sqrt {2\alpha sr} + \frac{\delta k}{2}\cdot\left( {\frac{{\beta \left( {1 - t} \right)\left( {\alpha c - A} \right)}}{{\beta^{2} \left( {1 - t} \right) - 4\alpha k\left( {1 - \delta t} \right)}}} \right)^{2}$, $g_{2} \left( {w,L} \right) < 0$ holds.

When parameters meet both $g_{1} \left( {w_{\Delta } ,L} \right) < 0$ and $g_{2} \left( {w,L} \right) < 0$, that is $s + S_{R}^{0} < {\text{min}}\left( {2sr + S_{M0} - \frac{{\left( {c\beta^{2} \left( {1 - t} \right) - A4k\left( {1 - \delta t} \right)} \right)\cdot\left( {\alpha c - A} \right)4\alpha k\left( {1 - \delta t} \right)}}{{2\left( {\beta^{2} \left( {1 - t} \right) - 4\alpha k\left( {1 - \delta t} \right)} \right)^{2} }} + \frac{\delta k}{2}\cdot\left( {\frac{{\beta \left( {1 - t} \right)\left( {\alpha c - A} \right)}}{{\beta^{2} \left( {1 - t} \right) - 4\alpha k\left( {1 - \delta t} \right)}}} \right)^{2} ,c\sqrt {2\alpha sr} + \frac{\delta k}{2}\cdot\left( {\frac{{\beta \left( {1 - t} \right)\left( {\alpha c - A} \right)}}{{\beta^{2} \left( {1 - t} \right) - 4\alpha k\left( {1 - \delta t} \right)}}} \right)^{2} } \right)$, we have feasible solution 1.

After $w$ and $L$ are determined, according to the retailer’s response function, we can get the product price, and finally get the following result.

$$ \left\{ {\begin{array}{*{20}l} {p^{*} = \frac{{\left( {3Ak + ck\alpha } \right)\left( {1 - t\delta } \right) - c\left( {1 - t} \right)\beta^{2} }}{{4k\alpha \left( {1 - t\delta } \right) - \left( {1 - t} \right)\beta^{2} }}} \hfill \\ {L^{*} = \frac{{\left( {1 - t} \right)\left( {A - c\alpha } \right)\beta }}{{4k\alpha \left( {1 - t\delta } \right) - \left( {1 - t} \right)\beta^{2} }}} \hfill \\ {w_{\Delta }^{*} = \frac{{2k\left( {1 - t\delta } \right)\left( {A + \alpha \left( {c - 2\Delta } \right)} \right) - \left( {1 - t} \right)\beta^{2} \left( {c - \Delta } \right)}}{{4k\alpha \left( {1 - t\delta } \right) - \left( {1 - t} \right)\beta^{2} }}} \hfill \\ \end{array} } \right. $$

(A7.17)

(2), the KKT conditions satisfied by the optimal solution are as follows.

$$ \left\{ {\begin{array}{*{20}l} {\frac{{\partial {\mathcal{L}}}}{{\partial w_{\Delta } }} = \left( {A - \frac{{A + w_{\Delta } \alpha + L\beta }}{2} + L\beta - \left( {w_{\Delta } - c} \right)\frac{\alpha }{2}} \right)\left( {1 - t} \right) + \lambda_{1} c\alpha = 0} \hfill \\ {\frac{{\partial {\mathcal{L}}}}{\partial L} = \frac{\beta }{2}\left( {w_{\Delta } - c} \right)\left( {1 - t} \right) - kL\left( {1 - \delta t} \right) - \lambda_{1} \beta = 0} \hfill \\ {\frac{{\partial {\mathcal{L}}}}{{\partial \lambda_{1} }} = cq - S_{M0} + S_{R}^{0} + s = 0} \hfill \\ \end{array} } \right. $$

(A7.18)

The solution satisfying the above formula is as follows.

$$ \left\{ {\begin{array}{*{20}l} {\lambda_{1} = \frac{{\left( {2S_{M0} - 2S_{R}^{0} - 2s - cA + \alpha c^{2} } \right) \cdot k\alpha \left( {1 - \delta t} \right) - \frac{{\beta^{2} }}{2}\left( {S_{M0} - S_{R}^{0} - s} \right) \cdot \left( {1 - t} \right)}}{{\alpha \left( {\beta^{2} \left( {\frac{{c\left( {1 - t} \right)}}{2} - 1} \right) - \alpha ck\left( {1 - \delta t} \right)} \right)}}} \hfill \\ {w = \frac{{\frac{{\left( {2S_{M0} - 2S_{R}^{0} - 2s - cA + \alpha c^{2} } \right) \cdot k\alpha \left( {1 - \delta t} \right) - \frac{{\beta^{2} }}{2}\left( {S_{M0} - S_{R}^{0} - s} \right) \cdot \left( {1 - t} \right)}}{{\alpha \left( {\beta^{2} \left( {\frac{{c\left( {1 - t} \right)}}{2} - 1} \right) - \alpha ck\left( {1 - \delta t} \right)} \right)}}\alpha c^{2} + S_{M0} - S_{R}^{0} - s + \alpha c^{2} - \Delta \alpha c}}{\alpha c}} \hfill \\ {L = \frac{{2S_{M0} - 2S_{R}^{0} - 2s - cA + \left( {\frac{{\left( {2S_{M0} - 2S_{R}^{0} - 2s - cA + \alpha c^{2} } \right) \cdot k\alpha \left( {1 - \delta t} \right) - \frac{{\beta^{2} }}{2}\left( {S_{M0} - S_{R}^{0} - s} \right) \cdot \left( {1 - t} \right)}}{{\alpha \left( {\beta^{2} \left( {\frac{{c\left( {1 - t} \right)}}{2} - 1} \right) - \alpha ck\left( {1 - \delta t} \right)} \right)}} + 1} \right)\alpha c^{2} }}{c\beta }} \hfill \\ \end{array} } \right. $$

(A7.19)

Verification of $g_{2} \left( {w,L} \right) < 0$. $g_{2} \left( {w,L} \right) = s + S_{R}^{0} - w_{\Delta } q < s + S_{R}^{0} - cq - \frac{{\delta kL^{2} }}{2} < s + S_{R}^{0} - c\sqrt {2\alpha sr} - \frac{\delta k}{2} \cdot \left( {\frac{{\beta \left( {1 - t} \right)\left( {\alpha c - A} \right)}}{{\beta^{2} \left( {1 - t} \right) - 4\alpha k\left( {1 - \delta t} \right)}}} \right)^{2}$. Because $g_{1} \left( {w_{\Delta } ,L} \right) = cq - S_{M0} + S_{R}^{0} + s = 0 \Leftrightarrow cq = S_{M0} - S_{R}^{0} - s$, then, $g_{2} \left( {w,L} \right) < s + S_{R}^{0} - \left( {S_{M0} - S_{R}^{0} - s} \right) - \frac{{\delta kL^{2} }}{2} = 2s + 2S_{R}^{0} - S_{M0} - \frac{\delta k}{2}\left( {\frac{{2S_{M0} - 2S_{R}^{0} - 2s - cA + \left( {\frac{{\left( {2S_{M0} - 2S_{R}^{0} - 2s - cA + \alpha c^{2} } \right) \cdot k\alpha \left( {1 - \delta t} \right) - \frac{{\beta^{2} }}{2}\left( {S_{M0} - S_{R}^{0} - s} \right) \cdot \left( {1 - t} \right)}}{{\alpha \left( {\beta^{2} \left( {\frac{{c\left( {1 - t} \right)}}{2} - 1} \right) - \alpha ck\left( {1 - \delta t} \right)} \right)}} + 1} \right)\alpha c^{2} }}{c\beta }} \right)^{2}$. If the whole references value makes bellowed inequation hold, $2s + 2S_{R}^{0} < S_{M0} + \frac{\delta k}{2}\left( {\frac{{2S_{M0} - 2S_{R}^{0} - 2s - cA + \left( {\frac{{\left( {2S_{M0} - 2S_{R}^{0} - 2s - cA + \alpha c^{2} } \right) \cdot k\alpha \left( {1 - \delta t} \right) - \frac{{\beta^{2} }}{2}\left( {S_{M0} - S_{R}^{0} - s} \right) \cdot \left( {1 - t} \right)}}{{\alpha \left( {\beta^{2} \left( {\frac{{c\left( {1 - t} \right)}}{2} - 1} \right) - \alpha ck\left( {1 - \delta t} \right)} \right)}} + 1} \right)\alpha c^{2} }}{c\beta }} \right)^{2}$, we have solution 2 to be feasible.

The product price decision is the same as in scenario (1).

(3) $\lambda_{1} = 0,\lambda_{2} > 0$, the KKT conditions satisfied by the optimal solution are as follows.

$$ \left\{ {\begin{array}{*{20}l} {\frac{{\partial {\mathcal{L}}}}{{\partial w_{\Delta } }} = \left( {A - \frac{{A + w_{\Delta } \alpha + L\beta }}{2} + L\beta - \left( {w_{\Delta } - c} \right)\frac{\alpha }{2}} \right)\left( {1 - t} \right) + \lambda_{2} \left( {q - \alpha w_{\Delta } } \right) = 0} \hfill \\ {\frac{{\partial {\mathcal{L}}}}{\partial L} = \frac{\beta }{2}\left( {w_{\Delta } - c} \right)\left( {1 - t} \right) - kL\left( {1 - \delta t} \right) + \lambda_{2} \beta w_{\Delta } = 0} \hfill \\ {\frac{{\partial {\mathcal{L}}}}{{\partial \lambda_{2} }} = s + S_{R}^{0} - w_{\Delta } q = 0} \hfill \\ \end{array} } \right. $$

(A7.20)

Verification of $g_{1} \left( {w,L} \right) < 0$. $g_{1} \left( {w_{\Delta } ,L} \right) = cq - S_{M0} + S_{R}^{0} + s < \frac{{\left( {A + \beta L} \right)\left( {A + \beta L - \alpha w_{\Delta } } \right)}}{\alpha } - 2sr - \frac{{\delta kL^{2} }}{2} - S_{M0} + S_{R}^{0} + s = \frac{{\left( {A + \beta L} \right)\left( {A + \beta L - \frac{L\beta + \alpha c + A}{2}} \right)}}{\alpha } - 2sr - \frac{{\delta kL^{2} }}{2} - S_{M0} + S_{R}^{0} + s$, insert $L^{*}$ into the left equation.

When parameters meet $\frac{{\left( {A + \beta L} \right)\left( {A + \beta L - \alpha c} \right)}}{2\alpha } - \frac{{\delta kL^{2} }}{2} < 2sr + S_{M0} - S_{R}^{0} - s$, $g_{1} \left( {w_{\Delta } ,L} \right) < 0$ and there exists feasible solution 3.

The product price decision is the same as in scenario (1).

(4) $\lambda_{1} > 0,\lambda_{2} > 0$, the KKT conditions satisfied by the optimal solution are as follows.

$$ \left\{ {\begin{array}{*{20}l} {\frac{{\partial {\mathcal{L}}}}{{\partial w_{\Delta } }} = \left( {A - \frac{{A + w_{\Delta } \alpha + L\beta }}{2} + L\beta - \left( {w_{\Delta } - c} \right)\frac{\alpha }{2}} \right)\left( {1 - t} \right) + \lambda_{1} c\alpha + \lambda_{2} \left( {q - \alpha w_{\Delta } } \right) = 0} \hfill \\ {\frac{{\partial {\mathcal{L}}}}{\partial L} = \frac{\beta }{2}\left( {w_{\Delta } - c} \right)\left( {1 - t} \right) - kL\left( {1 - \delta t} \right) - \lambda_{1} \beta + \lambda_{2} \beta w_{\Delta } = 0} \hfill \\ {\frac{{\partial {\mathcal{L}}}}{{\partial \lambda_{1} }} = cq - S_{M0} + S_{R}^{0} + s = 0} \hfill \\ {\frac{{\partial {\mathcal{L}}}}{{\partial \lambda_{2} }} = s + S_{R}^{0} - w_{\Delta } q = 0} \hfill \\ \end{array} } \right. $$

(A7.21)

When $\lambda_{1}$ and $\lambda_{2}$ are greater than 0, then there is a feasible solution 4.

The product price decision is the same as in scenario (1).

1.8 Appendix 8

$\frac{{\partial p^{*} }}{\partial t} = \frac{{3\left( {c\alpha - A} \right)k\beta^{2} \left( {1 - \delta } \right)}}{{\left( {4k\alpha \left( {1 - t\delta } \right) - \left( {1 - t} \right)\beta^{2} } \right)^{2} }}$, the denominator must be greater than zero. If $\frac{{\partial p^{*} }}{\partial t} = 0$, and $\alpha$ is taken as unknown variable, we have $\alpha = \frac{{\text{A}}}{c}$. With $\alpha = \frac{A}{c}$ as the boundary, the sign for $\frac{{\partial p^{*} }}{\partial t}$ is greater than zero when $\alpha$ is on the right side of $\frac{A}{c}$. Conversely, the sign for $\frac{{\partial p^{*} }}{\partial t}$ is smaller than zero when $\alpha$ is on the left side of $\frac{A}{c}$. That is, when $\alpha > \frac{A}{c}$, there is $\frac{{\partial p^{*} }}{\partial t} > 0$, then $p^{*}$ increases in $t$, when $\alpha < \frac{A}{c}$, we have $\frac{{\partial p^{*} }}{\partial t} < 0$, then $p^{*}$ decreases in $t$.

1.9 Appendix 9

$\frac{{\partial p^{*} }}{\partial \beta } = \frac{{6k\beta \left( {1 - t\delta } \right)\left( {1 - t} \right)}}{{\left( {4k\alpha \left( {1 - t\delta } \right) - \left( {1 - t} \right)\beta^{2} } \right)^{2} }}\left( {A - c\alpha } \right)$, the denominator must be greater than zero, if $\frac{{\partial p^{*} }}{\partial \beta } = 0$, and $\alpha$ is taken as unknown variable, we also have $\alpha = \frac{{\text{A}}}{c}$. With $\alpha = \frac{A}{c}$ as the boundary, the sign for $\frac{{\partial p^{*} }}{\partial \beta }$ is greater than zero when $\alpha$ is on the left side of $\frac{A}{c}$. Conversely, the sign for $\frac{{\partial p^{*} }}{\partial \beta }$ is smaller than zero when $\alpha$ is on the right side of $\frac{A}{c}$. That is, when $\alpha < \frac{A}{c}$, $\frac{{\partial p^{*} }}{\partial \beta } > 0$, then $p^{*}$ increases in $\beta$; when $\alpha > \frac{A}{c}$, $\frac{{\partial p^{*} }}{\partial \beta } < 0$, then $p^{*}$ decreases in $\beta$.

1.10 Appendix 10

$\frac{{\partial w^{*} }}{\partial t} = - \frac{{2k\left( {A - c\alpha } \right)\beta^{2} \left( {1 - \delta } \right)}}{{\left( {4k\alpha \left( {1 - t\delta } \right) - \left( {1 - t} \right)\beta^{2} } \right)^{2} }}$. Taking $\alpha$ is the unknown variable and solve the left equation we can get the result: when $c = \frac{A}{\alpha }$, $\frac{{\partial w^{*} }}{\partial t} = 0$. The result implies the possibility of piecewise monotonicity. With $\alpha = \frac{A}{c}$ as the boundary, the sign for $\frac{{\partial w^{*} }}{\partial t}$ is greater than zero when $\alpha$ is on the right side of $\frac{A}{c}$. Conversely, the sign for $\frac{{\partial w^{*} }}{\partial t}$ is smaller than zero when $\alpha$ is on the left side of $\frac{A}{c}$. That is, when $\alpha > \frac{A}{c}$, we have $\frac{{\partial w^{*} }}{\partial t} > 0$, then $w^{*}$ increases in $t$; when $\alpha < \frac{A}{c}$, there is $\frac{{\partial w^{*} }}{\partial t} < 0$, then $w^{*}$ decreases in $t$.

$\frac{{\partial w^{*} }}{\partial \delta } = \frac{{2k\left( {1 - t} \right)t\left( {A - c\alpha } \right)\beta^{2} }}{{\left( {4k\alpha \left( {1 - t\delta } \right) - \left( {1 - t} \right)\beta^{2} } \right)^{2} }}$, the denominator must be greater than zero. Take the $\alpha$ as the uniquely unknown variable and when $\frac{{\partial w^{*} }}{\partial \delta } = 0$. Then, we can also get the same result $\alpha = \frac{A}{c}$ as the above equation. With $\alpha = \frac{A}{c}$ as the boundary, the sign for $\frac{{\partial w^{*} }}{\partial \delta }$ is greater than zero when $\alpha$ is on the left side of $\frac{A}{c}$. Conversely, the sign for $\frac{{\partial w^{*} }}{\partial \delta }$ is smaller than zero when $\alpha$ is on the right side of $\frac{A}{c}$. That is, when $\alpha > \frac{A}{c}$, we have $\frac{{\partial w^{*} }}{\partial \delta } < 0$, then $w^{*}$ decreases in $\delta$; when $\alpha < \frac{A}{c}$, we have $\frac{{\partial w^{*} }}{\partial \delta } > 0$, then $w^{*}$ increases in $\delta$.

1.11 Appendix 11

${ }\frac{{\partial L^{*} }}{\partial \delta } = \frac{{ - 4k\alpha t\left( {1 - t} \right)\left( {A - c\alpha } \right)\beta }}{{\left( {4k\alpha \left( {1 - t\delta } \right) - \left( {1 - t} \right)\beta^{2} } \right)^{2} }}$, the denominator must be greater than zero. Take the $\alpha$ as the uniquely unknown variable and when $\frac{{\partial L^{*} }}{\partial \delta } = 0$. Then, we can also get the same result $\alpha = \frac{A}{c}$. With $\alpha = \frac{A}{c}$ as the boundary, the sign for $\frac{{\partial L^{*} }}{\partial \delta }$ is greater than zero when $\alpha$ is on the right side of $\frac{A}{c}$. Conversely, the sign for $\frac{{\partial L^{*} }}{\partial \delta }$ is smaller than zero when $\alpha$ is on the left side of $\frac{A}{c}$. That is, when $\alpha < \frac{A}{c}$, there is $\frac{{\partial L^{*} }}{\partial \delta } < 0$, then $L^{*}$ decreases in $\delta$; when $\alpha > \frac{A}{c}$, there is $\frac{{\partial L^{*} }}{\partial \delta } > 0$, then $L^{*}$ increases in $\delta$.

1.12 Appendix 12

If $pq - s\left( {1 + r} \right) \le w_{{\tilde{\Delta }}} \cdot q - s - S_{R}^{0}$, it means that the retailer’s sales income is not enough to continue to pay the balance of the manufacturer’s trade credit after the bank loan is repaid. The retailer loses in the current period and does not need to pay taxes. When considering only a single period, we do not discuss the loss situation in depth, so the optimal decision process later in this section is ongoing under the premise of $pq - s\left( {1 + r} \right) \ge w_{{\tilde{\Delta }}} \cdot q - s - S_{R}^{0}$.

$$ \max S_{M} = \left( {w_{{\tilde{\Delta }}} - c} \right)q - \max \left( {t_{M} ,0} \right)t + S_{M0} - \frac{1}{2}kL^{2} $$

(A12.1)

$$ {\text{s}}.{\text{t}}.{\text{max }}S_{R} = pq - \max \left( {t_{R} ,0} \right)t - s\left( {1 + r} \right) - \left( {w_{{\tilde{\Delta }}} q - s - S_{R}^{0} } \right) $$

(A12.2)

$$ w_{{\tilde{\Delta }}} q \ge S_{R}^{0} + s $$

(A12.3)

$$ pq - s\left( {1 + r} \right) \ge w_{{\tilde{\Delta }}} q - s - S_{R}^{0} $$

(A12.4)

$$ cq \le S_{M0} + s + S_{R}^{0} $$

(A12.5)

First focus on the optimization problem of the retailer, the retailer’s profit function can be further expressed as

$$ \mathop {\max S_{R} }\limits_{{t_{R} > 0,w_{{\tilde{\Delta }}} q > S_{R}^{0} + s}} = p\left( {A - p\alpha + \beta L} \right) - \left( {\left( {p - \left( {w + \tilde{\Delta }} \right)} \right)\left( {A - p\alpha + \beta L} \right) - Sr} \right)t - S\left( {1 + r} \right) - \left( {\left( {A - p\alpha + \beta L} \right)w_{{\tilde{\Delta }}} - S} \right) + S_{R0} $$

(A12.6)

The first derivative and the second derivative of the retailer’s profit function with respect to the decision variables are as follows.

$$ \frac{{\partial S_{R} }}{\partial p} = A - 2p\alpha + L\beta - t\left( {A - p\alpha + L\beta - \alpha \left( {p - w - \tilde{\Delta }} \right)} \right) + \alpha \left( {w + \tilde{\Delta }} \right) $$

(A12.7)

$$ \frac{{\partial^{2} S_{R} }}{{\partial p^{2} }} = - 2\left( {1 - t} \right)\alpha < 0 $$

(A12.8)

Obviously, the retailer’s profit function is a concave function of $p$, and let the first derivative is equal to 0, we can get the reaction function, $p = \frac{{A + \alpha w + L\beta + \alpha \tilde{\Delta }}}{2\alpha }$.

We put the expression of w into $\mathop {{\text{maxS}}_{M}^{A} }\limits_{{t_{M} > 0,cq > s_{M0}^{A} }}$, then we have the following expression.

$$ \mathop {\max S_{M}^{A} }\limits_{{t_{M} > 0,cq > s_{M0}^{A} }} = \left( {\left( {\frac{{ - A + 2p\alpha - L\beta - \alpha \tilde{\Delta }}}{\alpha } + \tilde{\Delta }} \right) - c} \right)\left( {A - p\alpha + \beta L} \right) + S_{M0}^{A} - \left( {c\left( {A - p\alpha + \beta L} \right) - S_{M0}^{A} } \right)r_{s} - \left( {\left( {\left( {\frac{{ - A + 2p\alpha - L\beta - \alpha \tilde{\Delta }}}{\alpha } + \tilde{\Delta }} \right) - c} \right)\left( {A - p\alpha + \beta L} \right) - \left( {c\left( {A - p\alpha + \beta L} \right) - S_{M0}^{A} } \right)r_{s} - \frac{1}{2}\delta kL^{2} } \right)t - \frac{1}{2}kL^{2} $$

(A12.9)

The first derivative functions of the manufacturer’s profit function with respect to the decision variables are as follows.

$$ \frac{{\partial S_{M} }}{\partial w} = \left( {\frac{A}{2} - L\tilde{\Delta } + \frac{3}{2}L\beta - \alpha w - \alpha \tilde{\Delta } + \frac{{\alpha c\left( {1 + r_{s} } \right)}}{2}} \right)\left( {1 - t} \right) $$

(A12.10)

$$ \frac{{\partial S_{M} }}{\partial L} = \left( {t - 1} \right)\cdot\left( {\beta \left( {c - \tilde{\Delta } - w} \right) - \frac{\beta }{\alpha }\left( {\frac{{A + L\beta - \alpha \left( {w + \tilde{\Delta }} \right)}}{2}} \right) - c\beta r_{s} } \right) + \left( {t\delta - 1} \right)Lk $$

(A12.11)

The Hessian matrix of the manufacturer’s profit function on the decision variables is

$$ \left| {\begin{array}{*{20}c} {\frac{{\partial^{2} S_{M} }}{{\partial w^{2} }},} & {\frac{{\partial^{2} S_{M} }}{\partial w\partial L}} \\ {\frac{{\partial^{2} S_{M} }}{\partial L\partial w},} & {\frac{{\partial^{2} S_{M} }}{{\partial L^{2} }}} \\ \end{array} } \right| = \left| {\begin{array}{*{20}c} { - \left( {1 - t} \right)\alpha ,} & {\left( {\frac{3}{2}\beta - \tilde{\Delta }} \right)\left( {1 - t} \right)} \\ {\left( {\frac{3}{2}\beta - \tilde{\Delta }} \right)\left( {1 - t} \right),} & { - \frac{{\left( {1 - t} \right)\beta^{2} }}{2\alpha } - k\left( {1 - t\delta } \right)} \\ \end{array} } \right| $$

(A12.12)

Because of $\left| { - \left( {1 - t} \right)\alpha } \right| < 0$, so if $\alpha > \frac{{\left( { - 1 + t} \right)\left( {7\beta^{2} - 12\beta \tilde{\Delta } + 4\tilde{\Delta }^{2} } \right)}}{{4k\left( { - 1 + t\delta } \right)}}$, the above matrix is a negative definite matrix, $S_{M}$ is a joint concave function with respect to $w$ and $L$, both wholesale price $w$ and carbon emission reduction level $L$ has optimal solution.

The manufacturer’s maximum problem is equivalent to the following minimum problem. $\min - S_{M}^{A} = - \left( {\left( {w_{{\tilde{\Delta }}} - c} \right)q - \left( {cq - S_{M0}^{A} - s - S_{R}^{0} } \right)r_{s} - \left( {\left( {w_{{\tilde{\Delta }}} q - cq\left( {1 + r_{s} } \right) - \left( {S_{M0}^{A} + s + S_{R}^{0} } \right)r_{s} - \frac{{kL^{2} \delta }}{2}} \right)} \right)t - \frac{{kL^{2} }}{2}} \right)$. It is equivalent to that the objective function is a joint concave function, and the inequality constraint function $g_{1} = cq - S_{M0}^{A} + S_{R}^{0} + s$ is a linear function.

Construct the Lagrangian function as follows.

$$ {\mathcal{L}}\left( {w,L,\lambda_{1} ,\lambda_{2} } \right) = \left( {w + \tilde{\Delta } - c} \right)\left( {A + \beta L - \alpha \left( {w + \tilde{\Delta }} \right)} \right) - \left( {c\left( {A + \beta L - \alpha \left( {w + \tilde{\Delta }} \right)} \right) - S_{M0}^{A} - s - S_{R}^{0} } \right)r_{s} - \left( {\left( {w + \tilde{\Delta } - c\left( {1 + r_{s} } \right)} \right)\left( {A + \beta L - \alpha \left( {w + \tilde{\Delta }} \right)} \right) + \left( {S_{M0}^{A} + s + S_{R}^{0} } \right)r_{s} - \frac{{kL^{2} \delta }}{2}} \right)t - \frac{{kL^{2} }}{2} - \lambda_{1} \left( {c\left( {A + \beta L - \alpha \left( {w + \tilde{\Delta }} \right)} \right) - S_{M0}^{A} - S_{R}^{0} - s} \right) - \lambda_{2} \left( {s + S_{R}^{0} - w_{{\tilde{\Delta }}} \left( {A + \beta L - \alpha \left( {w + \tilde{\Delta }} \right)} \right)} \right) $$

(A12.13)

KKT conditions satisfied by the optimal solution:

$$ \left\{ {\begin{array}{*{20}l} {\frac{{\partial {\mathcal{L}}}}{{\partial w_{{\tilde{\Delta }}} }} = 0} \hfill \\ {\frac{{\partial {\mathcal{L}}}}{\partial L} = 0} \hfill \\ {\lambda_{j} \ge 0,j = 1,2} \hfill \\ {g_{j} \left( {w,L} \right) \le 0,j = 1,2} \hfill \\ {\lambda_{j} g_{j} \left( {w,L} \right) = 0,j = 1,2} \hfill \\ \end{array} } \right. $$

(A12.14)

(1) $\lambda_{1} = \lambda_{2} = 0$, in this case, both of the two constraints are relaxation conditions. The above conditions can be further simplified.

$$ \left\{ {\begin{array}{*{20}l} {\frac{{\partial {\mathcal{L}}}}{{\partial w_{{\tilde{\Delta }}} }} = \left( {\frac{A}{2} - L\tilde{\Delta } + \frac{3L\beta }{2} - \alpha w - \alpha \tilde{\Delta } + \frac{{\alpha c\left( {1 + r_{s} } \right)}}{2}} \right)\left( {1 - t} \right) = 0} \hfill \\ {\frac{{\partial {\mathcal{L}}}}{\partial L} = \left( {t - 1} \right)\cdot\left( {\beta \left( {c - \tilde{\Delta } - w} \right) - \frac{\beta }{\alpha }\left( {\frac{{A + L\beta - \alpha \left( {w + \tilde{\Delta }} \right)}}{2}} \right) - c\beta r_{s} } \right) + \left( {t\delta - 1} \right)Lk = 0} \hfill \\ \end{array} } \right. $$

(A12.15)

The solution satisfying the above formula is as follows.

$$ \left\{ {\begin{array}{*{20}l} {L^{*} = \frac{{\left( {1 - t} \right)\left( {A - c\alpha - c\alpha r_{s} } \right)\beta }}{{4k\alpha \left( {1 - t\delta } \right) - \left( {1 - t} \right)\beta^{2} }}} \hfill \\ {w^{*} = \frac{{2Ak\left( {1 - t\delta } \right) + c\left( {2k\alpha \left( {1 - t\delta } \right) - \left( {1 - t} \right)\beta^{2} } \right)\left( {1 + r_{s} } \right)}}{{4k\alpha \left( {1 - t\delta } \right) - \left( {1 - t} \right)\beta^{2} }} - \tilde{\Delta }} \hfill \\ \end{array} } \right. $$

(A12.16)

Because $t_{M} = \left( {w_{{\tilde{\Delta }}} - c} \right) \cdot q - \left( {cq - S_{M0}^{A} - s - S_{R}^{0} } \right)r_{s} - \frac{{kL^{2} \delta }}{2} > 0$, $t_{R} = \left( {p - w_{{\tilde{\Delta }}} } \right)q - sr > 0$. From the above result, we have $q = A + \beta L - \alpha w$ and $\left\{ {\begin{array}{*{20}l} {\left( {A + \beta L} \right)q > 2\alpha sr + \alpha \left( {w + \tilde{\Delta }} \right)q > 2\alpha sr + \alpha \left( {w + \tilde{\Delta } - c} \right)q} \hfill \\ {\left( {w_{{\tilde{\Delta }}} - c} \right) \cdot q - \left( {S_{M0}^{A} + S_{R}^{0} + s - cq} \right)r_{s} - \frac{{kL^{2} \delta }}{2} > 0} \hfill \\ \end{array} } \right.$, $g_{1} \left( {w_{{\tilde{\Delta }}} ,L} \right) = S_{M0}^{A} + S_{R}^{0} + s - cq < \left( {\frac{{\left( {A + \beta L} \right)\left( {A + \beta L - \alpha \left( {w + \tilde{\Delta }} \right)} \right)}}{\alpha } - 2sr - \frac{{\delta kL^{2} }}{2}} \right) \cdot \frac{1}{{r_{s} }}$ When $\frac{{\left( {A + \beta L^{*} } \right)\left( {A + \beta L^{*} - \alpha \left( {w^{*} + \tilde{\Delta }} \right)} \right)}}{\alpha } < 2sr + \frac{{\delta kL^{*2} }}{2}$ holds, we have $g_{1} \left( {w_{{\tilde{\Delta }}} ,L} \right) < 0$.

$g_{2} \left( {w,L} \right) = s + S_{R}^{0} - w_{{\tilde{\Delta }}} q$, When $s + S_{R}^{0} < \left( {w^{*} + \tilde{\Delta }} \right)\left( {A + \beta L^{*} - \alpha \left( {w^{*} + \tilde{\Delta }} \right)} \right)$ holds, we have $g_{2} \left( {w_{{\tilde{\Delta }}} ,L} \right) < 0$.

When the above two conditions are jointly satisfied, we have feasible solutions 1.

After $w$ and $L$ are determined, according to the retailer’s response function $p = \frac{A + \alpha w + L\beta }{{2\alpha }}$, we can get the product price, and finally get the following result.

$$ \left\{ {\begin{array}{*{20}l} {p^{*} = \frac{{k\left( {1 - t\delta } \right)\left( {3A + c\alpha + c\alpha r_{s} } \right) - c\left( {1 - t} \right)\left( {1 + r_{s} } \right)\beta^{2} }}{{4k\alpha \left( {1 - t\delta } \right) - \left( {1 - t} \right)\beta^{2} }}} \hfill \\ {L^{*} = \frac{{\left( {1 - t} \right)\left( {A - c\alpha - c\alpha r_{s} } \right)\beta }}{{4k\alpha \left( {1 - t\delta } \right) - \left( {1 - t} \right)\beta^{2} }}} \hfill \\ {w_{\Delta }^{*} = \frac{{2Ak\left( {1 - t\delta } \right) + c\left( {2k\alpha \left( {1 - t\delta } \right) - \left( {1 - t} \right)\beta^{2} } \right)\left( {1 + r_{s} } \right)}}{{4k\alpha \left( {1 - t\delta } \right) - \left( {1 - t} \right)\beta^{2} }} - \tilde{\Delta }} \hfill \\ \end{array} } \right. $$

(A12.17)

The product price decision is the same as in scenario (1).

(2) $\lambda_{1} > 0,\lambda_{2} = 0$.

$$ \left\{ {\begin{array}{*{20}l} {\frac{{\partial {\mathcal{L}}}}{{\partial w_{{\tilde{\Delta }}} }} = \left( {\frac{A}{2} - L\tilde{\Delta } + \frac{3L\beta }{2} - \alpha \left( {w + \tilde{\Delta }} \right) + \frac{{\alpha c\left( {1 + r_{s} } \right)}}{2}} \right)\left( {1 - t} \right) + \lambda_{1} \alpha = 0} \hfill \\ {\frac{{\partial {\mathcal{L}}}}{\partial L} = - \left( {1 - t} \right) \cdot \left( {\beta \left( {c - \tilde{\Delta } - w} \right) - \frac{\beta }{\alpha }\left( {\frac{{A + L\beta - \alpha \left( {w + \tilde{\Delta }} \right)}}{2}} \right) - c\beta r_{s} } \right) - \left( {1 - t\delta } \right)Lk - \lambda_{1} \beta = 0} \hfill \\ {\frac{{\partial {\mathcal{L}}}}{{\partial \lambda_{1} }} = c\left( {A + \beta L - \alpha \left( {w + \tilde{\Delta }} \right)} \right) - S_{M0}^{A} - S_{R}^{0} - s = 0} \hfill \\ \end{array} } \right. $$

(A12.18)

$g_{2} \left( {w,L} \right) = s + S_{R}^{0} - w_{{\tilde{\Delta }}} q$, When $s + S_{R}^{0} < \left( {w^{*} + \tilde{\Delta }} \right)\left( {A + \beta L^{*} - \alpha \left( {w^{*} + \tilde{\Delta }} \right)} \right)$ holds, we have $g_{2} \left( {w_{{\tilde{\Delta }}} ,L} \right) < 0$.

$g_{2} \left( {w,L} \right) < 0\tilde{\Delta }s + S_{R}^{0} < \frac{1}{\alpha }\left( {A + \beta L} \right)q - 2sr_{s}$. When $s + S_{R}^{0} < \frac{1}{\alpha }\left( {A + \beta L^{*} } \right)\left( {A + \beta L^{*} - \alpha \left( {w^{*} + \tilde{\Delta }} \right)} \right) - 2sr_{s}$ holds, we have $g_{2} \left( {w_{{\tilde{\Delta }}} ,L} \right) < 0$. we have feasible solutions 2.

The product price decision is the same as in scenario (1).

(3) ${ }\lambda_{1} = 0,\lambda_{2} > 0$.

$$ \left\{ {\begin{array}{*{20}l} {\frac{{\partial {\mathcal{L}}}}{{\partial w_{{\tilde{\Delta }}} }} = \left( {\frac{A}{2} - L\tilde{\Delta } + \frac{3L\beta }{2} - \alpha \left( {w + \tilde{\Delta }} \right) + \frac{{\alpha c\left( {1 + r_{s} } \right)}}{2}} \right)\left( {1 - t} \right) + \lambda_{2} \left( {A + \beta L - 2\alpha \left( {w + \tilde{\Delta }} \right)} \right) = 0} \hfill \\ {\frac{{\partial {\mathcal{L}}}}{\partial L} = - \left( {1 - t} \right)\cdot\left( {\beta \left( {c - \tilde{\Delta } - w} \right) - \frac{\beta }{\alpha }\left( {\frac{{A + L\beta - \alpha \left( {w + \tilde{\Delta }} \right)}}{2}} \right) - c\beta r_{s} } \right) - \left( {1 - t\delta } \right)Lk - \lambda_{2} \beta \left( {w + \tilde{\Delta }} \right) = 0} \hfill \\ {\frac{{\partial {\mathcal{L}}}}{{\partial \lambda_{2} }} = s + S_{R}^{0} - \left( {w + \tilde{\Delta }} \right)\left( {A + \beta L - \alpha \left( {w + \tilde{\Delta }} \right)} \right) = 0} \hfill \\ \end{array} } \right. $$

(A12.19)

$g_{1} \left( {w_{{\tilde{\Delta }}} ,L} \right) = S_{M0}^{A} + S_{R}^{0} + s - cq < \left( {\frac{{\left( {A + \beta L} \right)\left( {A + \beta L - \alpha \left( {w + \tilde{\Delta }} \right)} \right)}}{\alpha } - 2sr - \frac{{\delta kL^{2} }}{2}} \right) \cdot \frac{1}{{r_{s} }}$. When $\frac{{\left( {A + \beta L^{*} } \right)\left( {A + \beta L^{*} - \alpha \left( {w^{*} + \tilde{\Delta }} \right)} \right)}}{\alpha } < 2sr + \frac{{\delta kL^{*2} }}{2}$ holds, we have $g_{1} \left( {w_{{\tilde{\Delta }}} ,L} \right) < 0$, and it has the feasible solution 2. The results have been put on record for checking, but they are not included in the appendix for too long.

(4) ${ }\lambda_{1} > 0,\lambda_{2} > 0$.

$$ \left\{ {\begin{array}{*{20}l} {\frac{{\partial {\mathcal{L}}}}{{\partial w_{{\tilde{\Delta }}} }} = \left( {\frac{A}{2} - L\tilde{\Delta } + \frac{3L\beta }{2} - \alpha \left( {w + \tilde{\Delta }} \right) + \frac{{\alpha c\left( {1 + r_{s} } \right)}}{2}} \right)\left( {1 - t} \right) + \lambda_{1} \alpha + \lambda_{2} \left( {A + \beta L - 2\alpha \left( {w + \tilde{\Delta }} \right)} \right) = 0} \hfill \\ {\frac{{\partial {\mathcal{L}}}}{\partial L} = - \left( {1 - t} \right) \cdot \left( {\beta \left( {c - \tilde{\Delta } - w} \right) - \frac{\beta }{\alpha }\left( {\frac{{A + L\beta - \alpha \left( {w + \tilde{\Delta }} \right)}}{2}} \right) - c\beta r_{s} } \right) - \left( {1 - t\delta } \right)Lk - \lambda_{1} \beta - \lambda_{2} \beta \left( {w + \tilde{\Delta }} \right) = 0} \hfill \\ {\frac{{\partial {\mathcal{L}}}}{{\partial \lambda_{1} }} = c\left( {A + \beta L - \alpha \left( {w + \tilde{\Delta }} \right)} \right) - S_{M0}^{A} - S_{R}^{0} - s = 0} \hfill \\ {\frac{{\partial {\mathcal{L}}}}{{\partial \lambda_{2} }} = s + S_{R}^{0} - \left( {w + \tilde{\Delta }} \right)\left( {A + \beta L - \alpha \left( {w + \tilde{\Delta }} \right)} \right) = 0} \hfill \\ \end{array} } \right. $$

(A12.20)

When both $\lambda_{1}$ and $\lambda_{2}$ are bigger than zero, we have feasible solution 4.

The product price decision is the same as in scenario (1).

1.13 Appendix 13

$\frac{{\partial p^{*} }}{\partial \beta } = \frac{{6k\left( {1 - t} \right)\beta \left( {1 - t\delta } \right)\left( {A - c\alpha \left( {1 + r_{s} } \right)} \right)}}{{\left( {4k\alpha \left( {1 - t\delta } \right) - \left( {1 - t} \right)\beta^{2} } \right)^{2} }}$. Take the $\alpha$ as the uniquely unknown variable and when $\frac{{\partial p^{*} }}{\partial \beta } = 0$. Then, we get the result $\alpha = \frac{A}{{c\left( {1 + r_{s} } \right)}}$ as the above equation. With $\alpha = \frac{A}{{c\left( {1 + r_{s} } \right)}}$ as the boundary, the sign for $\frac{{\partial p^{*} }}{\partial \beta }$ is greater than zero when $\alpha$ is on the left side of $\frac{A}{{c\left( {1 + r_{s} } \right)}}$. Conversely, the sign for $\frac{{\partial p^{*} }}{\partial \beta }$ is smaller than zero when $\alpha$ is on the right side of $\frac{A}{{c\left( {1 + r_{s} } \right)}}$. That is, when $\alpha < \frac{A}{{c\left( {1 + r_{s} } \right)}}$, $\frac{{\partial p^{*} }}{\partial \beta } > 0$ holds, then $p^{*}$ increases in $\beta$; when $\alpha > \frac{A}{{c\left( {1 + r_{s} } \right)}}$, $\frac{{\partial p^{*} }}{\partial \beta } < 0$ holds, then $p^{*}$ decreases in $\beta$.

1.14 Appendix 14

$\frac{{\partial w^{*} }}{\partial t} = \frac{{2k\beta^{2} \left( {1 - \delta } \right)\left( {c\alpha \left( {1 + r_{s} } \right) - A} \right)}}{{\left( {4k\alpha \left( {1 - t\delta } \right) - \left( {1 - t} \right)\beta^{2} } \right)^{2} }}$, taking the $r_{s}$ as the uniquely unknown variable and when $\frac{{\partial w^{*} }}{\partial t} = 0$. Then, we get the result $r_{s} = \frac{A}{c\alpha } - 1$ as the above equation. With $r_{s} = \frac{A}{c\alpha } - 1$ as the boundary, the sign for $\frac{{\partial w^{*} }}{\partial t}$ is greater than zero when $r_{s}$ is on the right side of $\frac{A}{c\alpha } - 1$. Conversely, the sign for $\frac{{\partial w^{*} }}{\partial t}$ is smaller than zero when $r_{s}$ is on the left side of $\frac{A}{c\alpha } - 1$. That is, when $r_{s} > \frac{A}{c\alpha } - 1$, we can get $\frac{{\partial w^{*} }}{\partial t} > 0$, then $w^{*}$ increases in $t$; when $r_{s} < \frac{A}{c\alpha } - 1$, we have $\frac{{\partial w^{*} }}{\partial t} < 0$, then $w^{*}$ decreases in $t$.

$\frac{{\partial w^{*} }}{\partial \delta } = \frac{{2kt\beta^{2} \left( {1 - t} \right)\left( {A - c\alpha \left( {1 + r_{s} } \right)} \right)}}{{\left( {4k\alpha \left( {1 - t\delta } \right) - \left( {1 - t} \right)\beta^{2} } \right)^{2} }}$, taking the $r_{s}$ as the uniquely unknown variable and when $\frac{{\partial w^{*} }}{\partial \delta } = 0$. Then, we get the result $r_{s} = \frac{A}{c\alpha } - 1$ as the above equation. With $r_{s} = \frac{A}{c\alpha } - 1$ as the boundary, the sign for $\frac{{\partial w^{*} }}{\partial \delta }$ is greater than zero when $r_{s}$ is on the left side of $\frac{A}{c\alpha } - 1$. Conversely, the sign for $\frac{{\partial w^{*} }}{\partial \delta }$ is smaller than zero when $r_{s}$ is on the right side of $\frac{A}{c\alpha } - 1$. That is, when $r_{s} > \frac{A}{c\alpha } - 1$, we can get $\frac{{\partial w^{*} }}{\partial \delta } < 0$, then $w^{*}$ decreases in $\delta$; when $r_{s} < \frac{A}{c\alpha } - 1$, there is $\frac{{\partial w^{*} }}{\partial \delta } > 0$, then $w^{*}$ increases in $\delta$.

1.15 Appendix 15

$\frac{{\partial L^{*} }}{\partial \delta } = \frac{{4kt\left( {1 - t} \right)(A - c\alpha \left( {1 + r_{s} } \right)\alpha \beta }}{{\left( {4k\alpha \left( {1 - t\delta } \right) - \left( {1 - t} \right)\beta^{2} } \right)^{2} }}$. Taking the $c$ as the uniquely unknown variable and when $\frac{{\partial L^{*} }}{\partial \delta } = 0$, we can also get the same result $c = \frac{A}{{\alpha \left( {1 + r_{s} } \right)}}$ as the above equation. With $c = \frac{A}{{\alpha \left( {1 + r_{s} } \right)}}$ as the boundary, the sign for $\frac{{\partial L^{*} }}{\partial \delta }$ is greater than zero when $c$ is on the left side of $\frac{A}{{\alpha \left( {1 + r_{s} } \right)}}$. Conversely, the sign for $\frac{{\partial L^{*} }}{\partial \delta }$ is smaller than zero when $c$ is on the right side of $\frac{A}{{\alpha \left( {1 + r_{s} } \right)}}$. That is, when $c > \frac{A}{{\alpha \left( {1 + r_{s} } \right)}}$, then $L^{*}$ decreases in $\delta$; when $c < \frac{A}{{\alpha \left( {1 + r_{s} } \right)}}$, then $L^{*}$ increases in $\delta$.