Abstract
Despite the fact that medical responses are crucial for saving precious lives during any humanitarian crisis (e.g., the COVID-19 pandemic), healthcare infrastructure in many communities are partially covered or are not covered yet. In order to strengthen the health system response to such crisis, especially in low- to middle-income communities, this paper extends a novel multi-objective model for designing a health service network under uncertainty which simultaneously considers efficiency, social responsibility, and network cost. For efficiency, a modified data envelopment analysis model is introduced and inserted into the proposed model to decrease the inefficiency of healthcare facilities belonging to the different tiers of the health system. For social responsibility, two measures of job creation and balanced development are incorporated into the extended model. This is not only considered to cope with the increased numbers of patients and disaster victims to healthcare facilities but also to deal with the challenge of the economy and the livelihoods of people during the crisis. Moreover, a novel mixed possibilistic-flexible robust programming (MPFRP) approach is developed to protect the considered network against uncertainty. To show the applicability of the extended model, a real-world case study is presented. The results reveal that contrary to fuzzy programming models, the MPFRP performs well in terms of social responsibility (72%), cost (8%), and efficiency (28%) and is able to make a trade-off between these three measures. In this study, the resilience level of the designed network is not addressed while disregarding any short-term stoppage owing to internal or external sources of disruption in designing may bring about a considerable loss.
Keywords: Humanitarian operations, Health service network, Data envelopment analysis, Social responsibility, Multi-objective optimization, Mixed possibilistic-flexible robust programming
Introduction
Based on the report by WHO (https://www.who.int/emergencies/funding/response-plans), every year millions of people are in constant need of humanitarian aid, which can be associated, among other criteria, with conflicts, disease outbreaks, and natural disasters. Worldwide, and particularly in low- to middle-income communities, a serious health crisis can compromise the resilience of a country's health networks. For instance, the coronavirus disease-2019 (COVID-19) pandemic has put the health services of most countries in the world in a challenging situation. The infectious nature of the disease and the respiratory failure necessitating ventilatory care of these patients have put an extra burden on health service providers (Kumar et al., 2020; Xiang et al., 2020). Regarding such a problem, strengthening the health system response to such a crisis seems significant and undeniable (WHO, 2020).
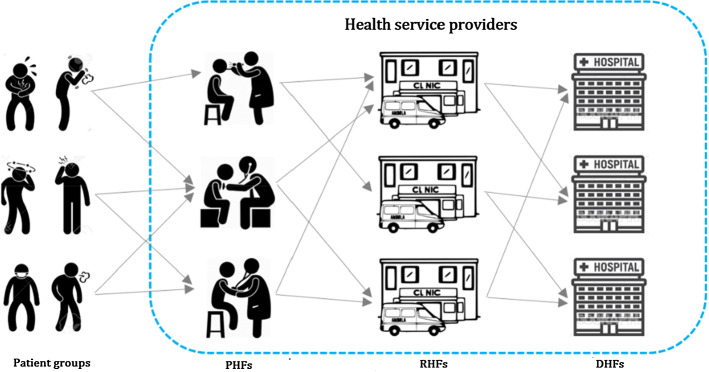
In general, a healthcare system in developing and developed countries is a three-tier hierarchical system that includes three types of health service providers (Mousazadeh et al., 2018a). At the beginning of this hierarchy, there are primary health facilities (PHFs). According to WHO, during a humanitarian health crisis such as the outbreak of the COVID-19 pandemic, an increasing number of people will seek health services. In this situation, if the entrance points of people with COVID-19 suspicion or symptoms to healthcare systems change from specialists service providers and hospitals into PHFs, it would have positive impacts on the total functionality of the healthcare systems and alleviate some of the burden on health facilities at the upper tiers (WHO, 2020). Considering this fact, patients first refer to their family physician/general practitioner, which is in charge of giving first aid or preventive care services, and then, in the case of need, refer to the upper tier of the health service network (HSN). According to World Health Report, the success of a health network based on the PHFs’ main role highly depends on the following arrangements: (1) bringing health services closer to people, (2) giving PHFs the responsibility for the care of the allocated population and (3) making PHFs’ role stronger as coordinators of the inputs of other tiers of the health system. At the second tier of such a hierarchical system, there are regional health facilities (RHFs) such as clinics that are responsible for those services that do not exist at the first tier, such as curative and limited therapeutic services. In addition, some people might visit the last tier, namely district health facilities (DHFs), such as specialty hospitals in which patients are provided with some specialized care services.
Social responsibility as a pillar of sustainability has to do with the force of non-governmental organizations to take responsibility for the social impacts of their activities (Zahiri et al., 2017). Community involvement and development is one of the important aspects of social responsibility as there is an agreement that the communities around the workplace should be promoted both economically and socially. In fact, the main goals of this feature include providing a balanced economic development as well as increasing job opportunities for local communities (Zhalechian et al., 2016).
The establishment of health facilities of any kind (either PHFs, RHFs, or DHFs) affects the regional development rate, especially in less developed areas. Based on WHO, there is an important relationship between economic development and health. In other words, better health makes a significant contribution to economic development, as it decreases production losses owing to worker illness, raises productivity, and it lowers absenteeism rates. Healthier workers could reasonably be expected to produce more output per hour worked. Productivity could be improved directly by enhanced mental and physical activity. Furthermore, more mentally and physically active workers could make more efficient and better use of equipment, machinery, and technology (WHO, 2001). In addition, more job opportunities are created for health workers out of opening health facilities, which in turn increase the ability of these centers to cope with the increased numbers of patients and disaster victims to healthcare facilities (Behl & Dutta, 2019; Wamba, 2020).
In the face of growing demand and rising cost pressures for care services during the humanitarian crisis, health policy-makers and managers are making a great effort to supply accessible, equitable, and high-quality care while protecting their long-term sustainability (Dubey & Altay, 2018; Dubey et al., 2019; Shibin et al., 2020). In this context, developing an appropriate technique to evaluate the efficiency of health service providers is crucial to correctly identify wasteful practice and design policy interventions that effectively improve efficiency. Data Envelopment Analysis (DEA) is an appropriate technique for this purpose. Compared to other techniques, it has some advantages, such as simultaneous use of multiple inputs and outputs (which may not be equal) to determine which units are performing most efficiently (Rezaei & Haeri, 2019).
Another important matter in the way of the health service network design (HSND) is to cope with an uncertain environment. Owing to the dynamic nature of the problem, most of the parameters like the opening cost of health facilities and the demand for care in different tiers of the HSN are uncertain. Under such circumstances, the robustness of the final solution is important because it deals with decisions such as capacity sizing and location–allocation that cannot be altered simply in a long-term horizon (Tofighi et al., 2016).
In this paper, a new multi-objective model is extended for designing an integrated socially responsible-efficient HSN with different types of healthcare facilities in response to the humanitarian crisis. To do so, a modified DEA model as well as two measures of social responsibility, including job creation and balanced development, are presented and incorporated into the extended model. Based on the authors’ knowledge, there is no HSND in the literature of humanitarian operations that simultaneously considered efficiency and social responsibility concepts in designing the HSN, while this paper is the first to tackle such a problem in the field of strengthening the health system response to the humanitarian crisis. To solve the extended multi-objective model and find the best candidate places for opening health service centers, an interactive fuzzy method [i.e., the Torabi–Hassini (TH) method] is also applied. Moreover, a novel mixed possibilistic-flexible robust programming (MPFRP) approach is presented to protect the considered network from uncertainty. The outcomes reveal that inserting DEA measures into HSND makes it possible to decrease the inefficiency of health service facilities and guarantees to deliver accessible, equitable, and high-quality care among all people, especially in deprived areas that suffer from rather unresponsive and inefficient healthcare systems. In case of social responsibility, the opening of new health facilities of any kind (either PHFs, RHFs, or DHFs) not only creates job opportunities for specialists and other health workers in response to the increased numbers of patients and disaster victims to healthcare facilities during the humanitarian crisis but also increases the development rate in less developed areas as it increases production through improving population health. To obtain some more results about the numerical findings, the performance of MPFRP models are compared against the performance of mixed possibilistic-flexible programming (MPFP). The achieved results indicate that compared with fuzzy programming models, MPFP, for instance, robust models (i.e., MPFRP), can usually provide better performance.
The remainder of the paper is organized as follows. A comprehensive literature review in the context of HSND is presented in Sect. 2. Section 3 is dedicated to problem description and mathematical model. The extended approach for coping with uncertainty along with solution methodology is presented in Sect. 4. Section 5 discussed a real case study to illustrate the problem applicability. Section 6 presents the results as well as a number of sensitivity analyses. Also, Sect. 7 is dedicated to discussion, and finally, Sect. 8 discusses the conclusion, limitations, and some future research avenues.
Literature review
In this section, the relevant papers on the subject of interest are divided into two major groups: (1) HSND problems and (2) humanitarian HSND problems. In continue, the research gaps and main contributions of this paper are described.
HSND problems
Making healthcare services accessible to all communities is an important prerequisite for a health system to achieve its goal known as “reducing health inequalities”. An excellent HSND is the main step for reaching this goal, which impacts greatly on the performance of the associated health system’s operations (Mousazadeh et al., 2016). Among the related studies in the field of HSND, there are a few studies that have focused on considering various healthcare facilities in different tiers of the HSN (Mousazadeh et al., 2018a, 2018b). Mousazadeh et al. (2018a) extended a mixed-integer nonlinear programming model (MINLP) for designing a three-tier HSN. Minimizing the distance between health facilities and patient groups as well as minimizing the total establishment cost were the objectives of their proposed model. The problem includes decisions on placing of PHFs, RHFs, and DHFs and determining their capacities at different tiers, assigning patient groups to the opened facilities, designing an efficient referral system, and the patients flow through the health network. A new hybrid robust possibilistic programming (PP) method was also introduced to tackle uncertainty in input parameters. Mousazadeh et al. (2018b) addressed a multi-objective MILP model to redesign a three-tier HSN in a multi-period planning horizon with the aim of maximizing the equity in the people's utilization of the health services and the access to the HSN and minimizing the total instability of HSN. Locating healthcare facilities (PHFs, RHFs, and DHFs), expanding or closing the capacity of facilities, reallocating patient groups to facilities, and redesigning an efficient referral system were considered as strategic decisions. To tackle different uncertainty, a mixed fuzzy-robust programming approach was also used.
In the case of social responsibility, the only studies that address this issue in HSND and planning are Zahiri et al. (2017), Eskandari-Khanghahi et al. (2018), and Pishvaee et al. (2014). Zahiri et al. (2017) developed a resilient-sustainable pharmaceutical network design with the objectives of minimizing de-resiliency, maximizing total sustainability with regard to maximizing social impacts and minimizing environmental impact, and minimizing total network cost. Objective functions (OFs) associated with the social impact of establishing facilities in the considered network attempts to maximize the balanced economic development and total created job opportunities. Eskandari-Khanghahi et al. (2018) extended a novel model to design a blood platelet supply chain network consisting of location, allocation, inventory, routing by inserting sustainability into the process of decision making. Maximizing social effects (including fixed jobs and variable jobs), minimizing the total cost, and environmental effects were taken into account as the objectives of the extended model. Pishvaee et al. (2014) extended a multi-objective PP model for designing a sustainable HSN under uncertainty in which four measures of social responsibility, including job opportunities, local development, damage to workers, and consumer risk, were taken into account.
The concept of efficiency as a basis to evaluate the performance of health service providers and decrease their inefficiency is a major issue in HSND and planning. In the case of efficient HSND, existing literature has a gap. Haeri et al. (2020a) provided a mixed efficient-resilient model to design a network of blood supply chain. An augmented form of DEA model was incorporated into the proposed model to determine the best sites for opening blood distribution centers, blood production centers, and blood collection centers in Iran considering three outputs of environmental actions, population density and education and culture of each region and two inputs of pollution and traffic.
Humanitarian HSND problems
Exploring the extant body of literature, the subsequent recent papers can be highlighted for HSND in humanitarian operations. Acar and Kaya (2019) introduced a HSND model to specify the locations and capacities of mobile hospitals to be opened before the crisis and relocation of these facilities to the suitable zones after the crisis using a stochastic programming approach. They applied their models for an expected earthquake. Minimizing the expected costs before and after the disaster was taken into account as the objectives of the extended model. Liu et al. (2019) extended a bi-objective optimization model for the design of a humanitarian medical rescue network. In the proposed model, they determined the temporary health service locations and allocation plan by minimizing the total operational cost and increasing the number of expected survivals in the way of using helicopters and ambulances. Gu et al. (2018) proposed a mathematical programming model for determining the places of temporary health relief shelters and maximize the number of patients who achieve health services at multiple health relief shelters under a limited relief budget. Cheraghi and Hosseini-Motlagh (2018) used a mixed-integer linear programming (MILP) formulation for designing a reliable and responsive injured-oriented blood supply chain network (BSCN) in the crisis considering three criteria including urgency, fairness, and risks. Samani et al. (2018) introduced a MILP multi-objective formulation for designing a BSCN in disaster relief with the aim of providing a tradeoff between the shortage and network cost efficiency while considering the uncertainty of demand and supply of blood. Kamyabniya et al. (2019) introduced a two-step coordination mechanism for platelets supply chain network in disaster relief in which the proposed approach aims to minimize cost and relief response time. Mohamadi and Yaghoubi (2017) developed a bi-objective stochastic model for designing an emergency HSN in a disaster considering important issues such as medical supplies and urgent health services. The proposed model determined the suitable locations of transfer zones and medical supplies distribution facilities. Minimizing travel time between health facilities and the total network costs were the objectives of their proposed model. Zarrinpoor et al. (2017) addressed a hierarchical location–allocation model for designing a HSN under the risk of disruptions. A two-stage robust method by taking into account a two-tier multi-flow nested hierarchy with service referral was applied to formulate the considered problem. As a solution approach, the authors presented a solution approach-based Benders decomposition method to solve the proposed model. Salehi et al. (2019) proposed a two-stage stochastic robust formulation to design a BSCN in the disaster in which the compatibility of blood groups and the pre-stock inventory were considered as the main contributions. Khalilpourazari and Khamseh (2019) extended a bi-objective formulation to design an emergency BSCN in an earthquake. Minimizing the total response time and the total cost were taken into account as objectives of the developed model. Sharma et al. (2019) extended a location-allocation approach for temporary blood centers after and during the disaster in which the proposed model seeks to minimize the maximum distance with hospitals. Fazli-Khalaf et al. (2019) extended a multi-objective formulation for a BSCN design in disaster with the objectives of minimizing the time of transportation and cost of considered network and maximizing the reliability of blood tested at laboratories. Khalilpourazari et al. (2020) presented a BSCN design in crisis considering different transportation modes. Minimizing the transportation time as well as the supply chain costs were taken into account as OFs of the developed model.
From reviewing above papers, the subsequent conclusions could be drawn.
First, while a few studies have investigated socially responsible HSND (Eskandari-Khanghahi et al., 2018; Pishvaee et al., 2014; Zahiri et al., 2017) and efficient HSND (Haeri et al., 2020a), the literature is scant on the integrated socially responsible-efficient HSN in response to the humanitarian crisis.
Second, many services/facilities are mentioned in the literature, including PHFs, RHFs (e.g., clinics), DHFs (e.g., specialty hospitals), community health centers, long-term care services, specialized health services, and emergency medical services. To the best of the authors’ knowledge, only a few studies have focused on considering various healthcare facilities from different tiers of the HSN (Mousazadeh et al., 2018a, 2018b) and the existing literature in humanitarian HSND has a gap.
Third, among the reviewed articles considering the data uncertainty (Acar & Kaya, 2019; Mohamadi & Yaghoubi, 2017; Mousazadeh et al., 2018a, 2018b; Pishvaee et al., 2014; Salehi et al., 2019; Samani et al., 2018; Zarrinpoor et al., 2017), robust programming and stochastic programming approaches have mostly been applied to handle uncertainty. Based on the authors’ knowledge, the only paper that addresses the mixed fuzzy-robust programming approach in HSND is Mousazadeh et al. (2018b). Interestingly, none of the articles in the literature of humanitarian HSND uses the mixed fuzzy-robust programming approach to handle uncertainty in data.
The findings obtained from the reviewed articles in humanitarian HSND indicate the narrow scope of efficiency and social responsibility, insufficient address of various facilities from different tiers of the HSN, and the lack of uncertainty consideration. This motivated us to introduce a new integrated socially responsible-efficient HSN with different types of healthcare facilities in response to the humanitarian crisis under uncertainty. This paper requires the answers to the below questions.
What are the effects of designing a multi-tier HSN under uncertainty by considering efficiency, social responsibility, and network cost?
Where to locate health centers and what capacities to allocate to them to meet the demand in the best way?
How to reduce the impacts of uncertainty on the HSN during the humanitarian crisis?
Incorporating efficiency into humanitarian HSND can decrease the inefficiency of health service facilities and guarantees to deliver accessible, equitable, and high-quality care among all people, especially in deprived areas that suffer from rather unresponsive and inefficient healthcare systems. In this regard, a modified DEA model is introduced and inserted into the extended model to find inefficient health facilities and minimize their inefficiencies. Compared to the basic DEA model, the introduced DEA model in this study is able to calculate the efficiencies of all DMUs at the same time in one linear model. On the other hand, as during a major health crisis like the COVID-19 pandemic, health care providers are on the front lines, considering the concept of social responsibility in humanitarian operations makes it possible to cope with the increased numbers of patients to healthcare facilities through creating more job opportunities for specialists and other health workers. In addition, it increases the development rate, especially in less developed areas, as it increases production through improving population health. Accordingly, the present work incorporates two measures of job creation and balanced development into the proposed model. Moreover, focusing on various facilities of different tiers of the HSN makes it possible to reduce surge capacity needs during the humanitarian crisis, ensure that health systems can cope, and prevent hospital care units from becoming overwhelmed. Finally, to protect the considered network from uncertainty, the present study develops a new MPFRP method that receives benefits from both robust and fuzzy programming approaches. The proposed approach can efficiently specify the optimal value of confidence levels relevant to imprecise input parameters and flexible constraints and adjust the deviation of OF value from its expected performance.
Problem definition and mathematical formulation
As a deprived province, Chaharmahal–Bakhtiari suffers from a rather unresponsive and inefficient healthcare system that requires particular attention to getting improved. Since the condition of healthcare systems is counted as an important factor in response to a humanitarian health crisis such as the COVID-19 pandemic, this study aims to focus on designing a HSN to make sustainable development in the healthcare system of the province.
In this paper, a mixed approach for designing a three-tier HSN is provided (see Fig. 1). The concerned network consists of the patient groups that use health services, PHFs, RHFs, and DHFs. Patients refer to PHFs like family physicians at the points of entrance to the health system to receive preventive and public health services. In this case, three scenarios may occur: (I) Patients leave the health network because of no extra need of health services from an upper level, (II) patients visit RHFs for more diagnostic purposes or to receive other non-surgical treatments after receiving the first aid from PHFs and (III) patients visit DHFs for specialty health services (surgical interventions) after receiving the first aid from PHFs and then extra services from RHFs.
Fig. 1.
An overview of the HSN
Important decisions to be made by the presented formulation are capacities and locations of health service centers at different tiers, the assignment of patient groups to the opened health centers in the first tier of hierarchy (PHFs), and the flow amount of patients in the entire network. In addition, the presented model focuses on two main goals in HSND. (1) Social responsibility, which focuses on job creation for health workers and raising regional development rate through improving population health, and (2) Efficiency, which focuses on minimizing the inefficiency of health facilities. It should be noted that since our study is case-based research, its key data-driven sources are the field experts. Therefore, the influential measures are driven according to the experts' knowledge and viewpoint. With regard to the judgment of experts from the Ministry of Health and Medical Education (MOHME) of Iran, two measures of efficiency and social responsibility are those with utmost importance and significant influence among the others in the current humanitarian HSND of Chaharmahal–Bakhtiari and thus have been included in this study. However, in other cases, these measures may change to fit the most suitable determinants according to the cases' requirements. For example, a measure such as an environment has been considered less important and thus excluded from incorporating into the model.
The main assumptions in the provided model are as below:
The demands of all opened health service providers (i.e., PHFs, RHFs, and DHFs) must be fulfilled.
There are not any pre-opened health service facilities, and all of them are to be newly opened. However, if there is any pre-opened facility in the network, simply the corresponding 0–1 opening variable is set as 1 in the model. Therefore, the proposed model can be simply used for the network expansion problems as well.
Each health facility is capitalized and can be established at one of the available capacity levels. Moreover, the capacity of PHFs and RHFs reflect the total visits of patients that can be well responded by the healthcare facility, while the capacity of DHFs matches the total respective hospital’s beds.
At each candidate location, at most, one facility from each kind of health service provider can be opened.
The maximum demand of each patient group for PHFs, RHFs, and DHFs is less than or equal to the capacity of the largest PHFs, RHFs, and DHFs, respectively.
The cost of opening a new health service provider in each candidate location is equal to fixed and setup costs besides the operational costs.
Notations
In this part, the notations utilized in the mathematical model are presented as below (symbol ~ indicates uncertain parameters):
Indices
Alternatives for the candidate locations of PHFs, and
Alternatives for the candidate locations of RHFs, and
Alternatives for the candidate locations of DHFs, and
Index of patients’ groups,
Indices of available capacity levels for establishing health facilities,
Index of inputs,
Index of outputs,
Index of DMUs,
Parameters
Amount of input for PHF
Amount of input for RHF
Amount of input for DHF
Amount of output for PHF
Amount of output for RHF
Amount of output for DHF
The capacity of opened PHFs at place with capacity
The capacity of opened RHFs at place with capacity
The capacity of opened DHFs at place with capacity n
Opening cost for each PHF at place with capacity
Opening cost for each RHF at place with capacity
Opening cost for each DHF at place with capacity
The average number of visits from patient group to a PHF
The average number of visits from a PHF to a RHF by a person in patient group
The average number of visits from a RHF to a DHF by a person in patient group
The population of patient group
Job creation number out of opening PHF with capacity level
Job creation number out of opening RHF with capacity level
Job creation number out of opening DHF with capacity level
Unemployment rate at candidate place
Unemployment rate at candidate place
Unemployment rate at candidate place
Regional economic value for PHF with capacity
Regional economic value for RHF with capacity
Regional economic value for DHF with capacity
Regional development factor at candidate location (0 )
Regional development factor at candidate location (0 )
Regional development factor at candidate location (0 )
The weighted sum of PHF
The weighted sum of RHF
The weighted sum of DHF
Variables
The level of inefficiency of PHF
The level of inefficiency of RHF
The level of inefficiency of DHF
Coefficient of input at PHF
Coefficient of input at RHF
Coefficient of input at DHF
Coefficient of output at PHF
Coefficient of output at RHF
Coefficient of output at DHF
The flow from patient group to PHF
The flow from patient group to RHF through PHF
The flow from patient group to DHF through PHF and RHF
1, if a PHF is opened at candidate place with capacity level , otherwise 0
1, if a RHF is opened at candidate place with capacity level , otherwise 0
1, if a DHF is opened at candidate place with capacity level , otherwise 0
Mathematical model
A new mathematical model for HSND is presented in this part considering the above notations where minimizing total network cost, maximizing social responsibility in terms of maximizing the employment and economic development, and minimizing inefficiency are considered as OFs.
Cost measure
The first OF, consisting of three terms, aims to minimize the total network cost consisting of opening costs of PHFs, RHFs, and DHFs.
| 1 |
Social responsibility measure
The second OF, consisting of two terms, is the social responsibility of opening health service providers in the network. According to ISO 26000, community involvement and development is one of the important features of social responsibility. Employment and balanced economic development are two main measures for calculating this aspect of social responsibility. In this regard, the first weighted term of the second OF tries to maximize the number of job creation out of opening health service providers considering the unemployment rate while the balanced economic development is maximized by the second term.
| 2 |
Considering the structure of the function, minimization of would lead to obtaining the maximum value for . To obtain the respective values of parameters and should be separately optimized under minimization (to obtain ) and maximization (to obtain ).
DEA measure
The third OF, consisting of three terms, maximizes the efficiencies of PHFs, RHFs, and DHFs, respectively. The proof is provided in “Appendix A”.
| 3 |
Constraints
| 4 |
| 5 |
| 6 |
| 7 |
Constraint (4) indicates that the sum of inputs of opened PHFs would be equal to 1, and otherwise, it would be 0. Based on the constraint (5), the sum of outputs of opened PHF would be equal to Constraints (6) and (7) show that the efficiency of each PHF must be smaller than 1.
| 8 |
| 9 |
| 10 |
| 11 |
Constraint (8) indicates that the sum of inputs of opened RHFs would be equal to 1, and otherwise, it would be 0. Based on the constraint (9), the sum of outputs of opened RHF would be equal to Constraints (10) and (11) show that the efficiency of each RHF must be smaller than 1.
| 12 |
| 13 |
| 14 |
| 15 |
Constraint (12) indicates that the sum of inputs of opened DHFs would be equal to 1, and otherwise, it would be 0. Based on the constraint (13), the sum of outputs of opened DHF l would be equal to Constraints (14) and (15) show that the efficiency of each DHF must be smaller than 1.
| 16 |
| 17 |
| 18 |
| 19 |
| 20 |
| 21 |
Constraints (16)–(21) describe the fact that if each health service facility, including PHFs, RHFs, and DHFs, opened, at least will have some input and output criteria.
| 22 |
| 23 |
| 24 |
Constraints (22)–(24) indicate constraints related to capacity and put limitations on entering flows to the PHFs, RHFs, and DHFs, respectively. In other words, they ensure that the entering flow from the lower level will not be greater than the service capacity of the relevant level.
| 25 |
| 26 |
| 27 |
Constraints (25)–(27) indicate demand fulfillment constraints and guarantee that all the demands must be fulfilled by PHFs, RHFs, and DHFs, respectively.
| 28 |
| 29 |
| 30 |
Constraints (28)–(30) show that each health facility, including PHF, RHF, and DHF, could be opened in one of the accessible service capacity levels.
Solution methodology
In this part, a novel MPFRP method is employed to solve the extended model. Afterward, the TH method introduced by Torabi and Hassini (2008) is utilized to tackle the multi-objective model (see Fig. 2).
Fig. 2.
Visual representation of the research method
Robust fuzzy mathematical programming model
There are three methods of fuzzy programming, robust optimization, and stochastic programming in the field of mathematical programming for coping with uncertainty. Each approach has its unique features which distinguish it from the others. According to the kind of uncertainty, the level of incompleteness in the parameters, and the context of the problem, one of these methods or a combination of them can be employed (Haeri et al., 2020b).
Flexible programming (FP) and PP approaches are two main classes of fuzzy programming in which the former cops with imprecise input parameters while the latter cops with flexibility on target value of goals and soft constraints. Similarly, robust FP and robust PP can be considered for robust fuzzy programming. In this study, a novel MPFRP is developed to receive the benefits of both robust and fuzzy programming approaches. The term robust refers to a solution that has both optimality robustness (the value of OF stays close to the optimal value for about all uncertain parameters) and feasibility robustness (the solution stays feasible for about all uncertain parameters). According to the steps provided in “Appendix B”, the proposed MPFRP is as below:
| 31 |
The first terms of each OF show the average performance of the studied network with respect to the expected value of uncertain parameters, while the second terms concentrate on minimizing the maximum deviation over the expected value of each OF and control the degree of optimality robustness. The importance of the second term is determined by parameter . The rest terms in the first OF focus on minimizing total penalty costs, in which the third and fourth terms adjust feasibility robustness related to the uncertainty of parameters, while the last two terms of this OF adjust the feasibility robustness relevant to the flexibility of soft constraints. The extension of the MPFRP model can eradicate the aforementioned imperfections of the basic MPFP model explained in “Appendix B” since the MPFRP model can efficiently specify the optimal value of confidence levels relevant to imprecise input parameters and flexible constraints and adjust the deviation of OF value from its expected performance.
Due to the multiplication of variables in the third constraint as well as the fifth and sixth terms of the first OF, model (31) is considered to be nonlinear. In this regard, the MPFRP model could be turned to the below linear model based on Lemma 1 explained in “Appendix B” and adding auxiliary variable .
| 32 |
The three new constraints guarantee that if the value of variable would always be equal to zero; otherwise, the auxiliary variable's value would be equal to the value of the variable.
In continue, two other versions of the model (32) are introduced, namely MPFRP I and MPFRP III, based on the conservatism level of the decision-makers (DMs) approaches towards the values of each OF, which vary in the second terms of the above OFs (i.e., the variation of objective values). Model (33) indicates the compact MPFRP I formulation as below:
| 33 |
Model (34) indicates the compact MPFRP III formulation as below:
| 34 |
Torabi and Hassini's method
Among the considered fuzzy approaches for solving multi-objective programming models in the literature, the TH method is the most suitable method since (I) its solutions are always efficient, (II) it can generate both balanced and unbalanced solutions according to the preferences of DMs, (III) its solutions match the preferences of DMs (i.e., the consistency between satisfaction and weight vectors), (IV) new efficient solutions can be obtained for a particular problem with a given weight vector via altering the value (Torabi & Hassini, 2008). It is noteworthy that the TH method has been widely used by researchers in the context of HSND (see, for instance, Cheraghi & Hosseini-Motlagh, 2018; Mousazadeh et al., 2018a; Samani et al., 2018; Haeri et al., 2020a). The formulation of the TH method introduced by Torabi and Hassini’s (2008) is as below:
| 35 |
In which represents the minimum satisfaction level of Z1, Z2 and Z3 and indicates the feasible area which encompasses the constraint of the equivalent crisp model. Additionally, and show the importance of objective function ℎ and the coefficient of compensation, respectively.
The case
To assess the performance and usefulness of the extended model and inspired by a real case, an integrated socially responsible-efficient HSN is designed for Chaharmahal–Bakhtiari province through close and effective collaboration with MOHME experts.
Chaharmahal–Bakhtiari, whose capital is Shahrekord, is regarded as one of the country's underprivileged areas with a population of 947,763 and 16,332 km2 of area. According to the evaluations of MOHME experts, the current HSN of this province is unable to respond to a humanitarian health crisis such as the COVID-19 pandemic and merits a special consideration to get improved since it suffers from quite unresponsive and inefficient healthcare facilities which lack advanced equipment and are mostly old. According to the knowledge of MOHME experts, these issues result from the fact that each town in this province does not have the appropriate budget and the required potential to open equipped health facilities. Also, in terms of human resources, each facility lacks enough doctors, especially specialists. At the moment, each facility has to increase health workers' shifts to provide patients with services, which in turn affects the mental health of health workers and decreases their productivity. Under such circumstances, poor treatment is given, and patients and their companions are dissatisfied with services. On the other hand, people in this province usually live far from health service providers, making it difficult and expensive to seek help when problems arise. They are more likely to go untreated and, therefore, to suffer from worse health. To tackle these challenges, MOHME has made a decision to design a HSN for Chaharmahal–Bakhtiari from the beginning by considering the concepts of efficiency and social responsibility so as to decrease the inefficiency of health facilities and improve the ability to cope with the increased numbers of patients and disaster victims to healthcare facilities during the humanitarian crisis (https://www.farsnews.com/chaharmahal-bakhtiari/news/13980330000869/).
To assist the authorities of MOHME in planning and designing the considered network, it is assumed that there is not any pre-opened health service providers, and the present study aims to design a three-tier HSN from the beginning. However, as mentioned earlier, if there is any pre-opened health service provider, simply the corresponding 0–1 opening variable is set as 1 in the model. As it can be seen from Fig. 3, this province of the country encompasses 29 towns, each of which is taken into account as a patient group and the initial candidate place for opening a PHF. In addition, towns 18, 27, 8, 11, 12, 15, 23, 16, 10, and 2 have been chosen as the initial candidate locations for opening RHFs, and towns 18, 27, 8, 23, and 2 have been selected for opening DHFs while taking into account population and geographical location of each town as important factors for selecting the candidate locations.
Fig. 3.
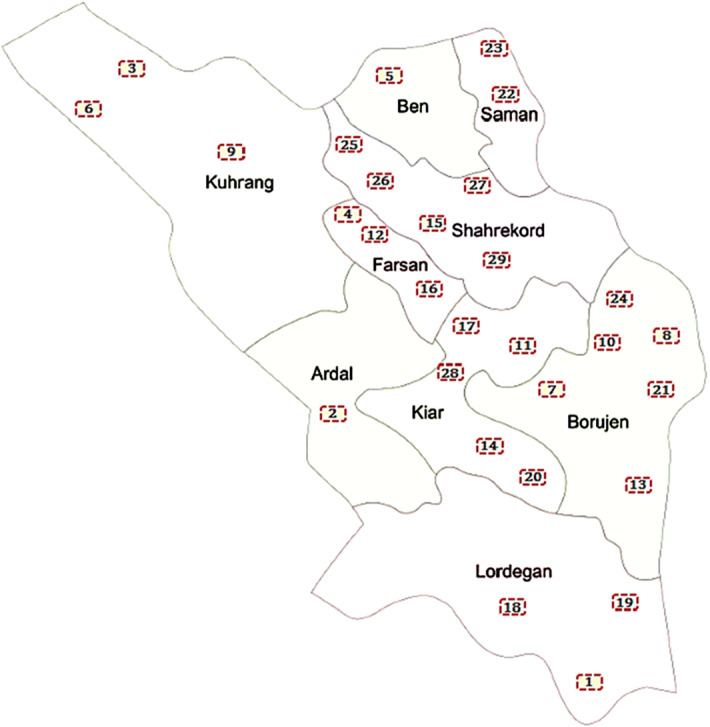
The boundary of the patient groups
Table 12 in Appendix C presents the population and geographic coordinates of each town (i.e., patient group) to estimate the number of visits to PHFs, RHFs, and DHFs.
Table 12.
Population and geographic coordinates of each patient group
| Patient group | Town name | Population () | Longitude | Latitude |
|---|---|---|---|---|
| 1 | Aloni | 2297 | 31.553067 | 51.058906 |
| 2 | Ardal | 8162 | 32.000902 | 50.645857 |
| 3 | Bazoft | 499 | 32.204449 | 50.046619 |
| 4 | Babaheidar | 10,922 | 32.329352 | 50.468123 |
| 5 | Ben | 11,699 | 32.542797 | 50.742931 |
| 6 | Biregan | 1670 | 32.448799 | 50.006824 |
| 7 | Boldaji | 10,905 | 31.938469 | 51.053488 |
| 8 | Boroujen | 49,077 | 31.975745 | 51.293449 |
| 9 | Chelgerd | 2708 | 32.463145 | 50.129062 |
| 10 | Faradonbeh | 12,697 | 32.009128 | 51.217060 |
| 11 | Farrokhshahr | 28,920 | 32.271381 | 50.973515 |
| 12 | Farsan | 26,219 | 32.256831 | 50.565562 |
| 13 | Gandoman | 5578 | 31.863596 | 51.154661 |
| 14 | Gahro | 6093 | 32.009731 | 50.885646 |
| 15 | Hafshejan | 20,042 | 32.226802 | 50.764474 |
| 16 | Jouneghan | 14,660 | 32.150599 | 50.585167 |
| 17 | Kian | 10,922 | 32.285155 | 50.891976 |
| 18 | Lordegan | 175,289 | 31.517597 | 50.820099 |
| 19 | Malkhalife | 2962 | 31.289626 | 51.262980 |
| 20 | Naghan | 4928 | 31.934558 | 50.729202 |
| 21 | Naghne | 8086 | 31.934008 | 51.329777 |
| 22 | Nafch | 3814 | 32.423550 | 50.787585 |
| 23 | Saman | 14,777 | 32.449384 | 50.911009 |
| 24 | Sefiddasht | 5880 | 32.133230 | 51.183618 |
| 25 | Soudejan | 5415 | 32.522029 | 50.399523 |
| 26 | Soureshjan | 11,124 | 32.314954 | 50.677228 |
| 27 | Shahrekord | 148,464 | 32.338101 | 50.856741 |
| 28 | Shalamzar | 7003 | 32.046169 | 50.816674 |
| 29 | Taghanak | 5504 | 32.218113 | 50.835935 |
Three possible capacities have been taken into account for opening different kinds of health service centers consisting PHFs, RHFs, and DHFs. In details, the first level of capacity for each candidate facility in each patient group is set as the minimum capacity that could fulfill the demand of the respective patient group, while based on the suggestion of MOHME's experts, the second and third levels of capacity could be defined such that each facility could support in average a number of nearby patient groups. The capacity of PHFs and RHFs reflect the total visits of patients that can be well responded by the healthcare facility, while the capacity of DHFs matches the total respective hospital beds.
According to the domain expert, an individual in each patient group will refer to a PHF an average of 1.265 times () a year. Taking this fact into account, each candidate PHF in each patient group could satisfy the demand of the relevant patient group in its first capacity level. To estimate the number of community health workers (CHW) in each PHF, it should be noted that this type of facility is typically operating for 250 days, and each CHW in these facilities can support around 20 patients in a working day. Additionally, according to the experts’ estimations, the second and third levels of capacity for PHFs are determined by considering this fact that on average, each facility could cover two or at most four nearby patient groups, respectively. Moreover, on average, the annual prorated costs of one CHW in each PHF is estimated at around 330 million rials for the first-level capacity according to the experts’ estimations which is reported in Table 1.
Table 1.
Possible capacity and cost for each PHF
| PHF | 1st capacity level | 2nd capacity level | 3rd capacity level | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Number of visits | Number of CHWs | Opening costs | Number of visits | Number of CHWs | Opening costs | Number of visits | Number of CHWs | Opening costs | |
| 1 | 2906 | 1 | 192 | 5811 | 2 | 384 | 11,623 | 4 | 767 |
| 2 | 10,325 | 3 | 681 | 20,650 | 6 | 1363 | 41,300 | 12 | 2726 |
| 3 | 631.2 | 1 | 41.7 | 1262 | 2 | 83.3 | 2524.9 | 4 | 167 |
| 4 | 13,816 | 3 | 912 | 27,633 | 6 | 1824 | 55,265 | 12 | 3648 |
| 5 | 14,799 | 3 | 977 | 29,598 | 6 | 1953 | 59,197 | 12 | 3907 |
| 6 | 2113 | 1 | 139 | 4225 | 2 | 279 | 8450.2 | 4 | 558 |
| 7 | 13,795 | 3 | 910 | 27,590 | 6 | 1821 | 55,179 | 12 | 3642 |
| 8 | 62,082 | 13 | 4097 | 124,165 | 26 | 8195 | 248,330 | 52 | 16,390 |
| 9 | 3426 | 1 | 226 | 6851 | 2 | 452 | 13,702 | 4 | 904 |
| 10 | 16,062 | 4 | 1060 | 32,123 | 8 | 2120 | 64,247 | 16 | 4240 |
| 11 | 36,584 | 8 | 2415 | 73,168 | 16 | 4829 | 146,335 | 32 | 9658 |
| 12 | 33,167 | 7 | 2189 | 66,334 | 14 | 4378 | 132,668 | 28 | 8756 |
| 13 | 7056 | 2 | 466 | 14,112 | 4 | 931 | 28,225 | 8 | 1863 |
| 14 | 7708 | 2 | 509 | 15,415 | 4 | 1017 | 30,831 | 8 | 2035 |
| 15 | 25,353 | 6 | 1673 | 50,706 | 12 | 3347 | 101,413 | 24 | 6693 |
| 16 | 18,545 | 4 | 1224 | 37,090 | 8 | 2448 | 74,180 | 16 | 4896 |
| 17 | 13,816 | 3 | 912 | 27,633 | 6 | 1824 | 55,265 | 12 | 3648 |
| 18 | 221,741 | 45 | 14,635 | 443,481 | 90 | 29,270 | 886,962 | 180 | 58,540 |
| 19 | 3747 | 1 | 247 | 7494 | 2 | 495 | 14,988 | 4 | 989 |
| 20 | 6234 | 2 | 411 | 12,468 | 4 | 823 | 24,936 | 8 | 1646 |
| 21 | 10,229 | 3 | 675 | 20,458 | 6 | 1350 | 40,915 | 12 | 2700 |
| 22 | 4825 | 1 | 318 | 9649 | 2 | 637 | 19,299 | 4 | 1274 |
| 23 | 18,693 | 4 | 1234 | 37,386 | 8 | 2467 | 74,772 | 16 | 4935 |
| 24 | 7438 | 2 | 491 | 14,876 | 4 | 982 | 29,753 | 8 | 1964 |
| 25 | 6850 | 2 | 452 | 13,700 | 4 | 904 | 27,400 | 8 | 1808 |
| 26 | 14,072 | 3 | 929 | 28,144 | 6 | 1857 | 56,287 | 12 | 3715 |
| 27 | 187,807 | 38 | 12,395 | 375,614 | 76 | 24,791 | 751,228 | 152 | 49,581 |
| 28 | 8859 | 2 | 585 | 17,718 | 4 | 1169 | 35,435 | 8 | 2339 |
| 29 | 6963 | 2 | 460 | 13,925 | 4 | 919 | 27,850 | 8 | 1838 |
As mentioned earlier, DMs determine ten initial candidate locations for opening RHFs in towns 18, 27, 8, 11, 12, 15, 23, 16, 10, and 2. Considering this fact that the opened RHFs must completely support 29 patient groups, each opened RHF should at least cover about three patient groups. According to the domain expert, on average, each visit to a PHF will be followed by 2.52 visits () to a RHF in a year. In addition, each RHF is typically operating for 250 days, and each doctor can support 30 patients in a working day. Accordingly, the first-level capacity of each candidate RHF is set. Furthermore, according to the experts’ estimations, the second capacity level and third capacity level for RHFs are determined by considering this fact that on average, each facility could support about six and nine nearby patient groups, respectively. Moreover, on average, the annual prorated costs of one doctor in each RHF for the first level of capacity is estimated at around 1200 million rials according to the experts’ estimations which is reported in Table 2.
Table 2.
Possible capacity and cost for each RHF
| RHF | 1st capacity level | 2nd capacity level | 3rd capacity level | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Number of visits | Number of doctors | Opening costs | Number of visits | Number of doctors | Opening costs | Number of visits | Number of doctors | Opening costs | |
| 18 | 558,787 | 75 | 89,406 | 1,117,575 | 150 | 178,812 | 1,676,362 | 225 | 268,218 |
| 27 | 473,274 | 64 | 75,724 | 946,547 | 128 | 151,448 | 1,419,821 | 192 | 227,171 |
| 8 | 156,447 | 21 | 25,031 | 312,893 | 42 | 50,063 | 469,340 | 63 | 75,094 |
| 11 | 92,192 | 13 | 14,751 | 184,383 | 26 | 29,501 | 276,575 | 39 | 44,252 |
| 12 | 83,581 | 12 | 13,373 | 167,162 | 24 | 26,746 | 250,743 | 36 | 40,119 |
| 15 | 63,890 | 9 | 10,222 | 127,779 | 18 | 20,445 | 191,669 | 27 | 30,667 |
| 23 | 47,106 | 7 | 7537 | 94,213 | 14 | 15,074 | 141,319 | 21 | 22,611 |
| 16 | 46,733 | 7 | 7477 | 93,467 | 14 | 14,955 | 140,200 | 21 | 22,432 |
| 10 | 40,476 | 6 | 6476 | 80,952 | 12 | 12,952 | 121,429 | 18 | 19,429 |
| 2 | 26,019 | 4 | 4163 | 52,038 | 8 | 8326 | 78,057 | 12 | 12,489 |
According to the domain expert, on average, each visit to a RHF will be followed by 0.065 () visits to a DHF in a year, and each DHF is typically operating in 365 days. Accordingly, the first-level capacity of each candidate DHF is set. Furthermore, according to the experts’ estimations, the second and third levels of capacity for DHFs are determined by multiplying the first-level capacity of each DHF by 1.5 and 2, respectively. Moreover, the opening cost of each DHF is computed considering operational costs of giving care to each patient and per bed equipment direct costs. The computed costs and capacities can be observed in Table 3.
Table 3.
Possible capacity and cost for each DHF
| DHF | 1st capacity level | 2nd capacity level | 3rd capacity level | |||
|---|---|---|---|---|---|---|
| Number of visits | Opening costs | Number of visits | Opening costs | Number of visits | Opening costs | |
| 18 | 36,321 | 316,328 | 54,482 | 474,492 | 72,642 | 632,656 |
| 27 | 30,763 | 366,807 | 46,144 | 550,210.5 | 61,526 | 733,614 |
| 8 | 10,169 | 624,327 | 15,254 | 936,490.5 | 20,338 | 1,248,654 |
| 23 | 3062 | 694,680 | 4593 | 1,042,020 | 6124 | 1,389,360 |
| 2 | 1691 | 815,811 | 2537 | 1,223,717 | 3382 | 1,631,622 |
Referring to the research of Hosseini-Motlagh et al. (2020) and based on the knowledge of MOHME experts, this study considers three inputs, namely traffic, pollution, and natural disasters incidence, and three outputs, namely population density, appropriate workplace, and skilled staff. According to the judgment of experts, these criteria are those with utmost importance and significant influence among the others in finding the best candidate places for health facilities and hence have been included in this paper:
Traffic
This criterion reflects the ease of access of patients to each level of the health network, i.e., PHFs, RHFs, and DHFs. The less the location congestion, the less the time and the energy required to reach each health facility, reflecting the superiority and inferiority of that facility. Hence, it is considered as an input criterion. The traffic is measured based on the average time a patient spends to reach each kind of health facility, i.e., PHF, RHF, and DHF.
Pollution
The place of the health centers should be carefully chosen so that they are removed from any direct sources of noise or air pollution such as vehicle emissions, construction, and industrial activities. The less the pollution, the more desirable the location for opening health facilities. Accordingly, this criterion is considered as an input criterion. The pollution is computed according to the pollution rate of each candidate location.
Population density
This criterion is the total individuals living per unit area. The more the population, the more the demand for health services, and the more the importance of health facilities in those locations. Therefore, this criterion is taken into account as an output criterion. The population density is computed according to the population around health centers.
Natural disasters incidence
This criterion shows that less disaster-prone places are better for opening health centers as they are less likely to be devastated because of disasters. With this assumption, this criterion is considered to be an input. The natural disaster incidence is estimated with respect to the number of faults close to health facilities.
Appropriate workplace
This criterion shows that places with better conditions in terms of temperature, natural light, humidity levels, etc., are more desirable for opening health facilities. As a result, this criterion is considered as an output. The appropriate workplace is estimated based on the experts' knowledge.
Skilled staff
This criterion shows that higher levels of skill are better because the proficiency of staff has a direct impact on the patient's satisfaction. As this criteria boost the facility's efficiency, it is considered as an output for PHFs, RHFs, and DHFs.
Computational results
The proposed model of this study is solved by GAMS 25.1.2. Also, a Laptop with 16 GB of RAM and Intel Core i7, 2.67 GHz CPU is used to implement all computational tests.
Analyzing the performance of the MPFRP model against the MPFP model
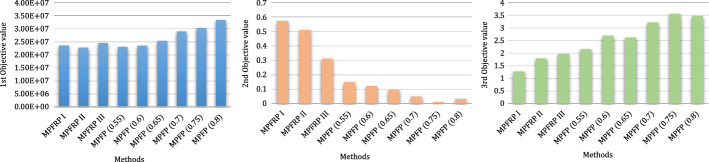
In this section, the effectiveness of the solutions obtained from the MPFRP model is shown in comparison with the MPFP model. Table 4 presents comparative results of the performance of ten approaches in which the first three approaches account for the robustness criterion and deal with the problem by different versions of MPFRP (i.e., MPFRP I, MPFRP II, and MPFRP III).
Table 4.
Comparative results of MPFRP and MPFP models
| Method | PHFs | RHFs | DHFs | Time | Gap (%) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MPFRP I | 2.3680E+7 | 0.573 | 1.272 | 0.726 | 0.726 | 0.728 | 0.880 | 15 | 8 | 4 | 0:01:57 | 0.0 |
| MPFRP II | 2.2739E+7 | 0.510 | 1.791 | 0.732 | 0.732 | 0.740 | 0.856 | 16 | 8 | 4 | 0:02:41 | 0.0 |
| MPFRP III | 2.4567E+7 | 0.311 | 1.968 | 0.736 | 0.737 | 0.736 | 0.856 | 16 | 7 | 4 | 0:02:39 | 0.0 |
| MPFP (0.55) | 2.3136E+7 | 0.150 | 2.154 | 0.738 | 0.738 | 0.739 | 0.850 | 17 | 9 | 4 | 0:05:38 | 0.0 |
| MPFP (0.6) | 2.3586E+7 | 0.122 | 2.682 | 0.753 | 0.757 | 0.753 | 0.840 | 20 | 8 | 3 | 0:02:25 | 0.0 |
| MPFP (0.65) | 2.5316E+7 | 0.096 | 2.606 | 0.757 | 0.757 | 0.758 | 0.868 | 19 | 9 | 4 | 0:03:56 | 0.0 |
| MPFP (0.7) | 2.8970E+7 | 0.051 | 3.212 | 0.732 | 0.732 | 0.734 | 0.878 | 23 | 9 | 4 | 0:03:35 | 0.0 |
| MPFP (0.75) | 3.0246E+7 | 0.011 | 3.555 | 0.745 | 0.745 | 0.746 | 0.872 | 23 | 8 | 4 | 0:02:45 | 0.0 |
| MPFP (0.8) | 3.3343E+7 | 0.033 | 3.469 | 0.717 | 0.731 | 0.717 | 0.879 | 23 | 10 | 4 | 0:04:48 | 0.0 |
| MPFP (> 0.85) | Infeasible |
The last seven approaches investigate the problem using MPFP models for various satisfaction levels (i.e., δ = σ = ρ = ξ = 0.55, 0.6, 0.65, 0.7, 0.75, 0.8), respectively. As can be observed from Table 4, MPFRP models have better performance in comparison with MPFP models. Increasing the satisfaction level from 0.55 to 0.8 will lead to a rise in the HSN cost because the model should satisfy the possibilistic constraints with a greater satisfaction level. On the other hand, increasing the satisfaction level will result in an increase in inefficiency and a decrease in social responsibility. As Table 4 represents, among the MPFP models, the MPFP under satisfaction level 0.55 has the lowest cost and inefficiency of all, whereas it has the highest social responsibility. MPFRP II performs better in terms of cost amid the MPFRP models since it has the lowest cost in comparison with MPFRP I and MPFRP III. In continue, more analyses are done on MPFRP II as this model indicates the best performance amid all the abovementioned MPSFP and MPSFRP models (Fig. 4).
Fig. 4.
Comparative results of MPFRP and MPFP models for each objective
Finding best-fit candidate locations for PHFs, RHFs, and DHFs
In this section, the best fit candidate places for PHFs, RHFs, and DHFs under different statuses are determined. A general understanding is that making a trade-off analysis between the values of OFs (cost, social responsibility, and inefficiency) can help DMs to make decisions about the best candidate places for health facilities.
Status (1): considering all three OFs with equal weights
As discussed earlier, the considered HSN wants to determine the best places for opening health service providers in such a way that inefficiency of health service centers is decreased while the social responsibility aspect of sustainability is increased during the crisis. For this purpose, according to the steps of the TH method (Torabi & Hassini, 2008), the best candidate places for opening health service centers are selected considering all three OFs with equal weights (see Fig. 5). As shown in Fig. 5, among 29 towns in Chaharmahal–Bakhtiari, eleven locations for establishing PHFs, seven places for RHFs, and three places for DHFs have been determined as the best fit.
Fig. 5.
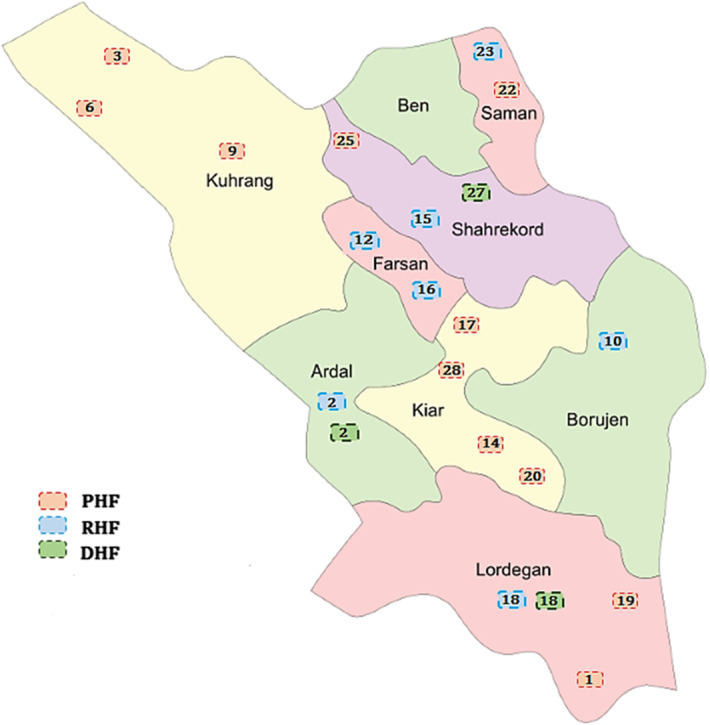
Best fit candidate places of PHFs, RHFs, and DHFs
Table 5 shows the scores of the best-fit candidate places of PHFs, RHFs, and DHFs in terms of inefficiency considering three inputs (Traffic, Pollution, and Natural disasters incidence) and three outputs (Population density, Appropriate workplace, and Skilled staff). As can be observed from Table 5, among eleven opened PHFs, eight PHFs (i.e., 1, 3, 6, 17, 19, 20, 22, and 25) have inefficiency scores equal to zero, while PHF (9), PHF (14) and PHF (28) have inefficiency scores equal to 0.123, 0.027 and 0.036, respectively. This means that eight opened PHFs with the inefficiency scores of zero use their inputs efficiently to achieve outputs and thus can be good benchmarks for the rest of the opened PHFs with higher inefficiency scores. In addition, all opened RHFs (i.e., 2, 10, 12, 15, 16, 18, and 23) and all opened DHFs (i.e., 2, 18, and 27) have inefficiency scores equal to zero, which ensure that they are able to deliver accessible, equitable and high-quality care in humanitarian operations.
Table 5.
Inefficiency scores and opened capacity levels of best-fit candidate locations for PHFs, RHFs, and DHFs
| PHFs | Town | Capacity | Inefficiency scores | RHFs | Town | Capacity | Inefficiency scores | DHFs | Town | Capacity | Inefficiency scores |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Aloni | 11,623 | 0 | 2 | Ardal | 78,057 | 0 | 2 | Ardal | 3382 | 0 |
| 3 | Bazoft | 2524.9 | 0 | 10 | Faradonbeh | 121,429 | 0 | 18 | Lordegan | 72,642 | 0 |
| 6 | Biregan | 8450.2 | 0 | 12 | Farsan | 250,743 | 0 | 27 | Shahrekord | 61,526 | 0 |
| 9 | Chelgerd | 13,702 | 0.123 | 15 | Hafshejan | 191,669 | 0 | ||||
| 14 | Gahro | 30,831 | 0.027 | 16 | Jouneghan | 140,200 | 0 | ||||
| 17 | Kian | 55,265 | 0 | 18 | Lordegan | 1,676,362 | 0 | ||||
| 19 | Malkhalife | 14,988 | 0 | 23 | Saman | 141,319 | 0 | ||||
| 20 | Naghan | 24,936 | 0 | ||||||||
| 22 | Nafch | 19,299 | 0 | ||||||||
| 25 | Soudejan | 27,400 | 0 | ||||||||
| 28 | Shalamzar | 35,435 | 0.036 |
The opened capacity levels of these centers are also presented in Table 5. As Table 5 represents, all health service centers are opened at capacity level 3, which means that each health center can support, on average several nearby patient groups based on the suggestions of DMs, which in turn increases job opportunities for specialists and other health workers.
Status (2): considering just cost and social responsibility measures with equal weights
In this state, just cost and social responsibility measures are considered to analyze the performance of health service facilities which lead to selecting nineteen locations for establishing PHFs, seven locations for RHFs, and three locations for DHFs (see Fig. 12 in Appendix C). The opened capacity levels of PHFs, RHFs, and DHFs under status (2) are also presented in Table 6. As Table 6 represents, all health service centers are opened at capacity level 3, similar to status (1).
Fig. 12.
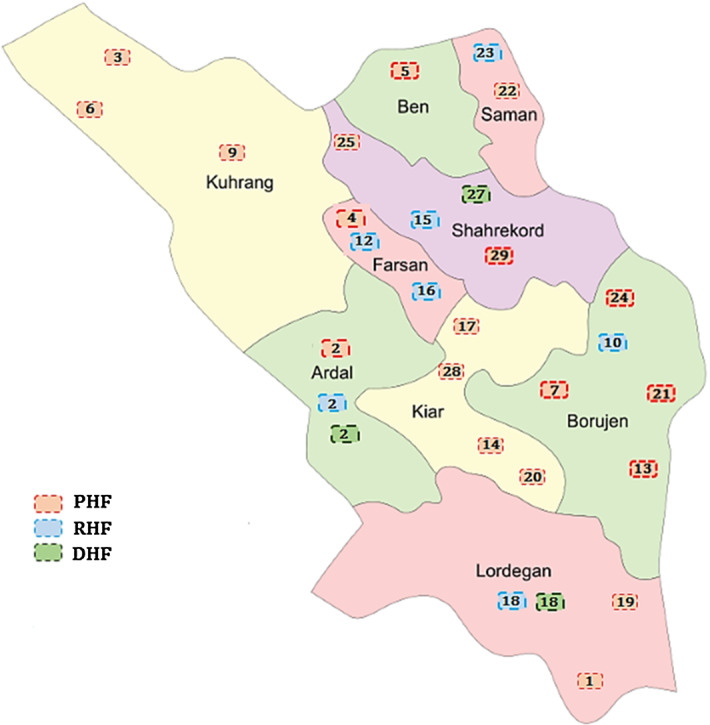
Best fit candidate locations for PHFs, RHFs, and DHFs based on status (2)
Table 6.
Opened capacity levels of PHFs, RHFs, and DHFs based on status (2)
| PHFs | Town | Capacity | RHFs | Town | Capacity | DHFs | Town | Capacity |
|---|---|---|---|---|---|---|---|---|
| 1 | Aloni | 11,623 | 2 | Ardal | 78,057 | 18 | Lordegan | 72,642 |
| 2 | Ardal | 41,300 | 10 | Faradonbeh | 121,429 | 27 | Shahrekord | 61,526 |
| 3 | Bazoft | 2524.9 | 12 | Farsan | 250,743 | 2 | Ardal | 3382 |
| 4 | Babaheidar | 55,265 | 15 | Hafshejan | 191,669 | |||
| 5 | Ben | 59,197 | 16 | Jouneghan | 140,200 | |||
| 6 | Biregan | 8450.2 | 18 | Lordegan | 1,676,362 | |||
| 7 | Boldaji | 55,179 | 23 | Saman | 141,319 | |||
| 9 | Chelgerd | 13,702 | ||||||
| 13 | Gandoman | 28,225 | ||||||
| 14 | Gahro | 30,831 | ||||||
| 17 | Kian | 55,265 | ||||||
| 19 | Malkhalife | 14,988 | ||||||
| 20 | Naghan | 24,936 | ||||||
| 21 | Naghne | 40,915 | ||||||
| 22 | Nafch | 19,299 | ||||||
| 24 | Sefiddasht | 29,753 | ||||||
| 25 | Soudejan | 27,400 | ||||||
| 28 | Shalamzar | 35,435 | ||||||
| 29 | Taghanak | 27,850 |
Status (3): considering just social responsibility and inefficiency measures with equal weights
In this state, just social responsibility and inefficiency measures are considered to analyze the performance of health service facilities which lead to selecting sixteen locations for establishing PHFs, nine locations for RHFs, and three locations for DHFs (see Fig. 13 in Appendix C). The opened capacity levels of PHFs, RHFs, and DHFs under status (3) are also presented in Table 7. As Table 7 represents, all health service facilities are opened at capacity level 3, similar to previous statuses.
Fig. 13.
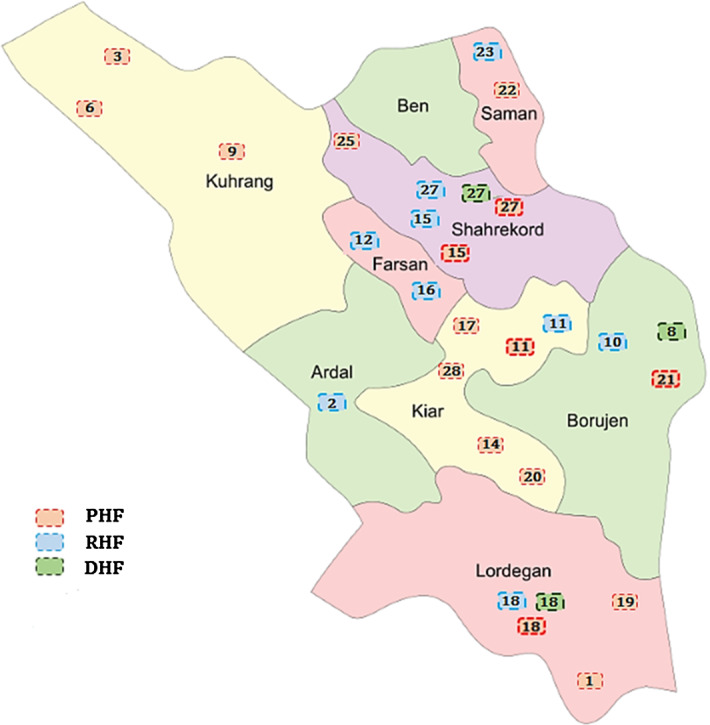
Best fit candidate locations for PHFs, RHFs, and DHFs based on status (3)
Table 7.
Opened capacity levels of PHFs, RHFs, and DHFs based on status (3)
| PHFs | Town | Capacity | RHFs | Town | Capacity | DHFs | Town | Capacity |
|---|---|---|---|---|---|---|---|---|
| 1 | Aloni | 11,623 | 2 | Ardal | 78,057 | 18 | Lordegan | 72,642 |
| 3 | Bazoft | 2524.9 | 10 | Faradonbeh | 121,429 | 27 | Shahrekord | 61,526 |
| 6 | Biregan | 8450.2 | 11 | Farrokhshahr | 276,575 | 8 | Boroujen | 20,338 |
| 9 | Chelgerd | 13,702 | 12 | Farsan | 250,743 | |||
| 11 | Farrokhshahr | 146,335 | 15 | Hafshejan | 191,669 | |||
| 14 | Gahro | 30,831 | 16 | Jouneghan | 140,200 | |||
| 15 | Hafshejan | 101,413 | 18 | Lordegan | 1,676,362 | |||
| 17 | Kian | 55,265 | 23 | Saman | 141,319 | |||
| 18 | Lordegan | 886,962 | 27 | Shahrekord | 1,419,821 | |||
| 19 | Malkhalife | 14,988 | ||||||
| 20 | Naghan | 24,936 | ||||||
| 21 | Naghne | 40,915 | ||||||
| 22 | Nafch | 19,299 | ||||||
| 25 | Soudejan | 27,400 | ||||||
| 27 | Shahrekord | 751,228 | ||||||
| 28 | Shalamzar | 35,435 |
Status (4): considering just cost and inefficiency measures with equal weights
In this state, just cost and inefficiency measures are taken into account to assess the performance of health service facilities which lead to selecting nine locations for establishing PHFs, three locations for RHFs, and one location for DHF (see Fig. 14 in Appendix C). The opened capacity levels of PHFs, RHFs, and DHFs under status (4) are also presented in Table 8. As Table 8 represents, in status 4, some PHFs are opened at capacity level 1, which means that these centers in each patient group can satisfy the demand of the relevant patient group. On the other hand, some PHFs in status 4 are opened at capacity levels 2 and 3. This means that these centers can support more patient groups with respect to the DMs' knowledge and viewpoint.
Fig. 14.
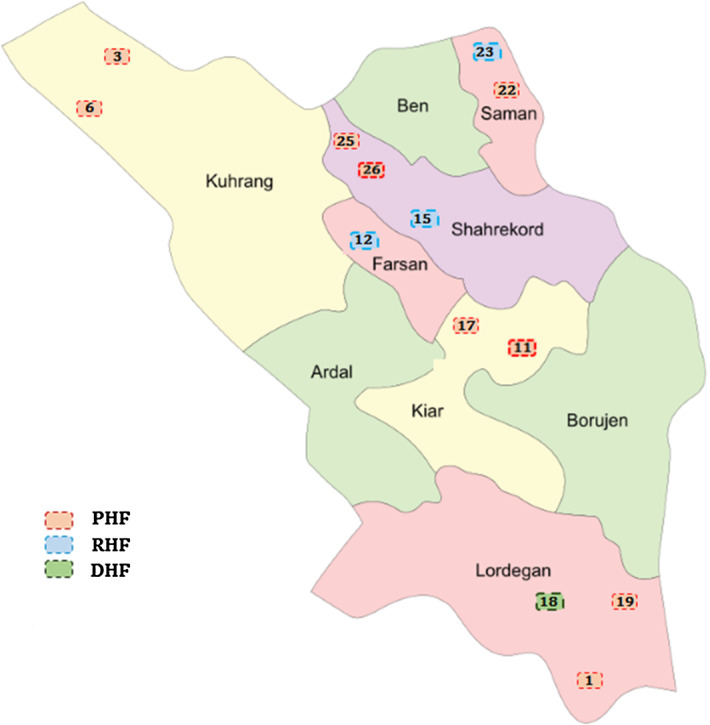
Best fit candidate locations for PHFs, RHFs, and DHFs based on status (4)
Table 8.
Opened capacity levels of PHFs, RHFs, and DHFs based on status (4)
| PHFs | Town | Capacity | RHFs | Town | Capacity | DHFs | Town | Capacity |
|---|---|---|---|---|---|---|---|---|
| 1 | Aloni | 2906 | 12 | Farsan | 83,581 | 18 | Lordegan | 72,642 |
| 3 | Bazoft | 1262 | 15 | Hafshejan | 63,890 | |||
| 6 | Biregan | 8450.2 | 23 | Saman | 94,213 | |||
| 11 | Farrokhshahr | 36,584 | ||||||
| 17 | Kian | 13,816 | ||||||
| 19 | Malkhalife | 7494 | ||||||
| 22 | Nafch | 4825 | ||||||
| 25 | Soudejan | 6850 | ||||||
| 26 | Soureshjan | 28,144 |
The performance of Z1, Z2 and Z3 under different statuses
In this part, the achieved values of Z1, Z2 and Z3 are examined in four statuses which are indicated in Table 9. As shown in Table 9, when just two measures of cost and social responsibility are considered, and inefficiency measure is ignored (status 2), the obtained values for Z3 (23.49) is the worst amid other statuses. In status 3, when just two measures of social responsibility and inefficiency are considered, and the measure of cost is ignored, Z2 obtains the best value (0.418) while Z1 achieves the worst one (6.0969E+7) in comparison with the other statuses. Also, considering two measures of cost and inefficiency together (status 1) lets Z2 obtains worse value (1.494) compared with other statuses while Z1 obtains the best value (3.9749E+6). Accordingly, as it is obvious, simultaneous considering of Z1, Z2 and Z3 (status 4) leads to more desirable results compared to the other statues.
Table 9.
The values of Z1, Z2 and Z3 under different statuses
| Status | Measures | The values of OFs | ||||
|---|---|---|---|---|---|---|
| Cost | Social responsibility | inefficiency | ||||
| 1 | ✓ | ✓ | 3.9749E+6 | 1.494 | 0.325 | |
| 2 | ✓ | ✓ | 2.3112E+7 | 0.482 | 23.49 | |
| 3 | ✓ | ✓ | 6.0969E+7 | 0.418 | 0.922 | |
| 4 | ✓ | ✓ | ✓ | 1.7279E+7 | 0.717 | 0.151 |
It is evident that the three OFs of the proposed model (i.e., cost, social responsibility, and efficiency) are in conflict with each other as an increase in the value of one may result in a decrease in the value of the other one. To be more specific, the cost OF has a tendency towards minimizing the total costs via opening fewer health facilities in the designed humanitarian HSN, while social responsibility has a tendency towards opening more health facilities to not only create more job opportunities for specialists and other health workers in response to the increased numbers of patients and disaster victims to healthcare facilities during the humanitarian crisis but also increase the development rate in less developed areas.
The first and third OFs also show a tendency of contradictions as an increase of efficiency leads to an increase in the total cost and vice versa. In fact, the efficiency has a tendency towards opening more health facilities to guarantee to deliver accessible, equitable, and high-quality care among all people, especially in deprived areas that suffer from rather unresponsive and inefficient healthcare systems, while the cost OF has a tendency towards network centralization through minimizing the total costs.
Analyzing the impacts of γ and θ
TH approach includes two main parameters of (objective importance) and (the coefficient of compensation). Altering the values of these two parameters according to the preference of DMs will result in getting a new efficient solution. In this section, the sensitivity of the model is analyzed by altering the values of these two parameters.
Figure 6 and Table 10 indicate the impact of altering the value of on the 1st term and 2nd term of TH model (). In Sect. 6.2, it was mentioned that Z1, Z2 and Z3 have equal weights in the design of the considered HSN while in real-life situations, they may not possess identical significance, and from the expert's viewpoint, one of them has more value. For example, as can be seen in Table 10, since Z1 in the fourth row has more value for the DM, it has been assigned more weight () in comparison with Z2 and Z3 or in the fifteenth row, since efficiency in the design of the considered HSN has more importance for the DM compared to the cost and social responsibility, it obtains more weight (). In addition, Table 10 indicates that an increase in the value of corresponds to an increase in the membership function value, which indicates the higher importance of OF. Therefore, altering this value allows the DMs to make a trade-off analysis between the values of with respect to their opinions.
Fig. 6.
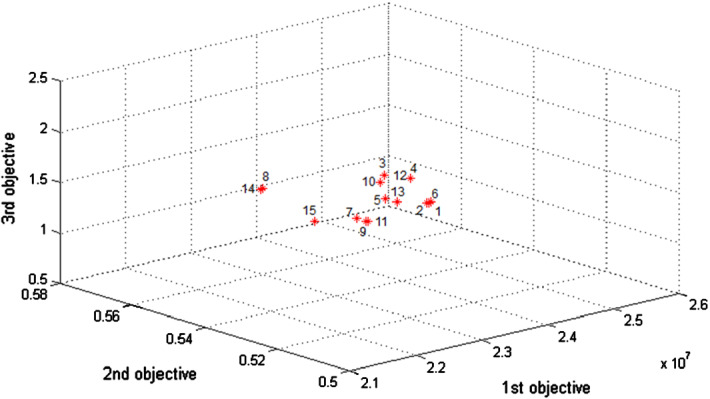
The values of Z1, Z2 and Z3according to different
Table 10.
The impacts of the OFs importance (θ) on the sensitivity of the model
| Number | PHFs | RHFs | DHFs | Time | Gap (%) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.33 | 0.33 | 0.33 | 0.732 | 2.2739E+7 | 0.510 | 1.791 | 0.732 | 0.740 | 0.856 | 16 | 7 | 4 | 0:02:41 | 0.0 |
| 2 | 0.5 | 0.2 | 0.3 | 0.732 | 2.2710E+7 | 0.510 | 1.791 | 0.732 | 0.740 | 0.856 | 16 | 8 | 4 | 0:03:33 | 0.0 |
| 3 | 0.6 | 0.2 | 0.2 | 0.741 | 2.1958E+7 | 0.508 | 2.201 | 0.742 | 0.741 | 0.816 | 16 | 8 | 4 | 0:02:26 | 0.0 |
| 4 | 0.7 | 0.2 | 0.1 | 0.740 | 2.2126E+7 | 0.504 | 2.189 | 0.740 | 0.744 | 0.817 | 18 | 7 | 3 | 0:02:41 | 0.0 |
| 5 | 0.4 | 0.3 | 0.3 | 0.735 | 2.2483E+7 | 0.517 | 1.791 | 0.735 | 0.735 | 0.856 | 16 | 8 | 4 | 0:02:49 | 0.0 |
| 6 | 0.3 | 0.4 | 0.3 | 0.732 | 2.2770E+7 | 0.510 | 1.791 | 0.732 | 0.740 | 0.856 | 16 | 7 | 4 | 0:02:40 | 0.0 |
| 7 | 0.3 | 0.3 | 0.4 | 0.724 | 2.2924E+7 | 0.533 | 1.357 | 0.730 | 0.724 | 0.898 | 15 | 8 | 4 | 0:02:25 | 0.0 |
| 8 | 0.2 | 0.5 | 0.3 | 0.727 | 2.1224E+7 | 0.528 | 1.964 | 0.752 | 0.727 | 0.839 | 17 | 7 | 3 | 0:02:32 | 0.0 |
| 9 | 0.2 | 0.3 | 0.5 | 0.722 | 2.3231E+7 | 0.536 | 1.250 | 0.726 | 0.722 | 0.909 | 15 | 8 | 4 | 0:02:27 | 0.0 |
| 10 | 0.3 | 0.5 | 0.2 | 0.738 | 2.2128E+7 | 0.512 | 2.059 | 0.740 | 0.738 | 0.830 | 17 | 7 | 4 | 0:02:30 | 0.0 |
| 11 | 0.3 | 0.2 | 0.5 | 0.722 | 2.3260E+7 | 0.536 | 1.250 | 0.725 | 0.722 | 0.909 | 15 | 8 | 4 | 0:02:40 | 0.0 |
| 12 | 0.2 | 0.6 | 0.2 | 0.740 | 2.2125E+7 | 0.504 | 2.189 | 0.740 | 0.744 | 0.817 | 18 | 7 | 3 | 0:02:41 | 0.0 |
| 13 | 0.2 | 0.2 | 0.6 | 0.695 | 2.5525E+7 | 0.569 | 0.735 | 0.695 | 0.699 | 0.959 | 14 | 9 | 4 | 0:02:43 | 0.0 |
| 14 | 0.1 | 0.7 | 0.2 | 0.727 | 2.1192E+7 | 0.528 | 1.964 | 0.753 | 0.727 | 0.839 | 17 | 7 | 3 | 0:02:58 | 0.0 |
| 15 | 0.1 | 0.2 | 0.7 | 0.695 | 2.4611E+7 | 0.575 | 0.613 | 0.707 | 0.695 | 0.971 | 13 | 8 | 5 | 0:02:43 | 0.0 |
Figure 7 and Table 11 indicate the impacts of altering the value of on the 1st term and 2nd term of TH model, considering . The 1st term aims to balance the membership function values of Z1, Z2 and Z3 and increase them while the 2nd term considers the weights of cost, social responsibility, and efficiency measures and gives priority to them. With this assumption, if DMs would like to have balanced, efficient solutions amid Z1, Z2 and Z3 and the achieved membership function values, the 1st term should get more weight (γ is increased) while if DMs would like to consider the weights of Z1, Z2 and Z3, the value of γ should be minimized so that the 2nd term will be more significant. As it can be seen from Table 11, by increasing the value of more weight are given to the trade-off between Z1, Z2 and Z3 and hence, the membership function values get closer to each other. On the other hand, by decreasing the importance is given to the objective with higher weight.
Fig. 7.
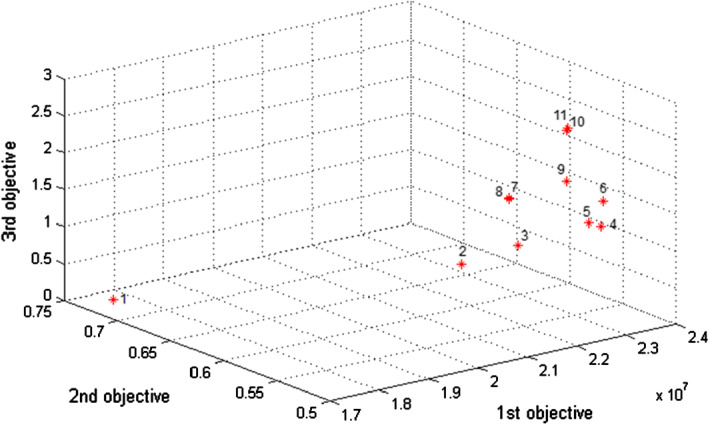
The values of Z1, Z2 and Z3 according to different γ
Table 11.
The impacts of compensation coefficients () on the sensitivity of the model
| Number | PHFs | RHFs | DHFs | Time | Gap (%) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0.33 | 0.33 | 0.33 | 0.598 | 1.7279E+7 | 0.717 | 0.151 | 0.804 | 0.598 | 1.000 | 11 | 7 | 3 | 0:02:42 | 0.0 |
| 2 | 0.1 | 0.679 | 2.1745E+7 | 0.598 | 0.613 | 0.745 | 0.679 | 0.971 | 13 | 8 | 4 | 0:02:36 | 0.0 | |||
| 3 | 0.2 | 0.701 | 2.2216E+7 | 0.566 | 0.982 | 0.739 | 0.701 | 0.935 | 14 | 8 | 4 | 0:02:41 | 0.0 | |||
| 4 | 0.3 | 0.722 | 2.3255E+7 | 0.536 | 1.238 | 0.725 | 0.722 | 0.910 | 15 | 8 | 4 | 0:02:44 | 0.0 | |||
| 5 | 0.4 | 0.724 | 2.2939E+7 | 0.533 | 1.357 | 0.729 | 0.724 | 0.898 | 15 | 8 | 4 | 0:02:32 | 0.0 | |||
| 6 | 0.5 | 0.732 | 2.2739E+7 | 0.510 | 1.791 | 0.732 | 0.740 | 0.856 | 16 | 7 | 4 | 0:02:41 | 0.0 | |||
| 7 | 0.6 | 0.727 | 2.1214E+7 | 0.528 | 1.964 | 0.752 | 0.727 | 0.839 | 17 | 7 | 3 | 0:02:31 | 0.0 | |||
| 8 | 0.7 | 0.727 | 2.1227E+7 | 0.528 | 1.952 | 0.752 | 0.727 | 0.840 | 17 | 7 | 3 | 0:02:28 | 0.0 | |||
| 9 | 0.8 | 0.741 | 2.1958E+7 | 0.508 | 2.189 | 0.742 | 0.741 | 0.817 | 18 | 7 | 3 | 0:02:37 | 0.0 | |||
| 10 | 0.9 | 0.742 | 2.1907E+7 | 0.506 | 2.911 | 0.743 | 0.742 | 0.746 | 20 | 7 | 4 | 0:02:32 | 0.0 | |||
| 11 | 1.0 | 0.743 | 2.1922E+7 | 0.505 | 2.945 | 0.743 | 0.743 | 0.743 | 20 | 7 | 3 | 0:02:23 | 0.0 |
Analyzing the effect of changes in capacity levels of opened health service centers
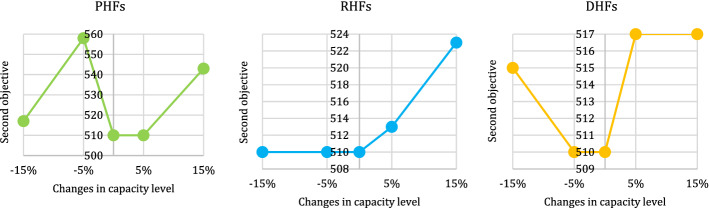
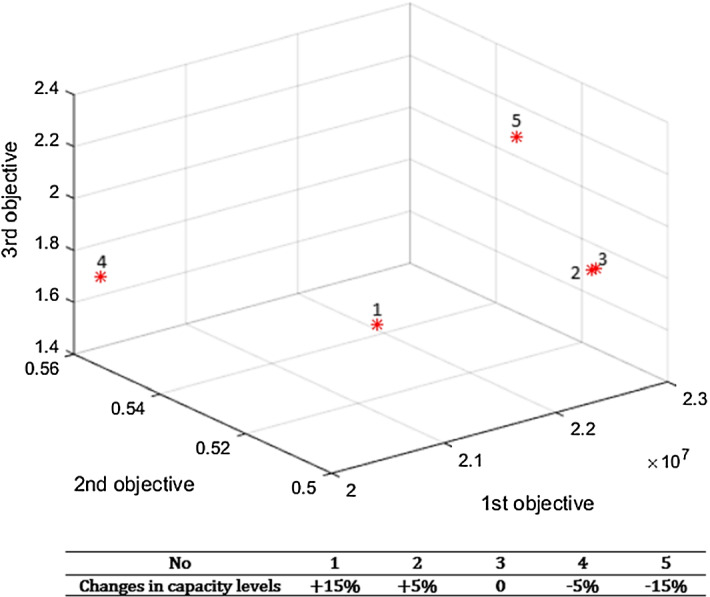
In this part, the effect of changes in capacity levels of opened PHFs, RHFs, and DHFs is analyzed (see Figs. 8, 9 and 10). As can be seen in Figs. 8, 9 and 10, increasing the capacity levels of opened health service centers from 5 to 15% will make a decrease in total cost (First OF) which could be due to a fewer number of centers needed to be established in the considered network. On the other hand, minimizing the capacity levels will lead to a higher number of health service centers needed, which can make an increase in total network cost. The overall effect of changes in capacity levels of opened health service centers on second and third OFs is such that both of them are not facing a major change, and this can indicate that the DM can make a decrease in total network cost by taking into account the higher level of capacity for health service centers and without a major change in the other two OFs.
Fig. 8.
The effect of changes in capacity levels of opened PHFs on the objective’s value
Fig. 9.
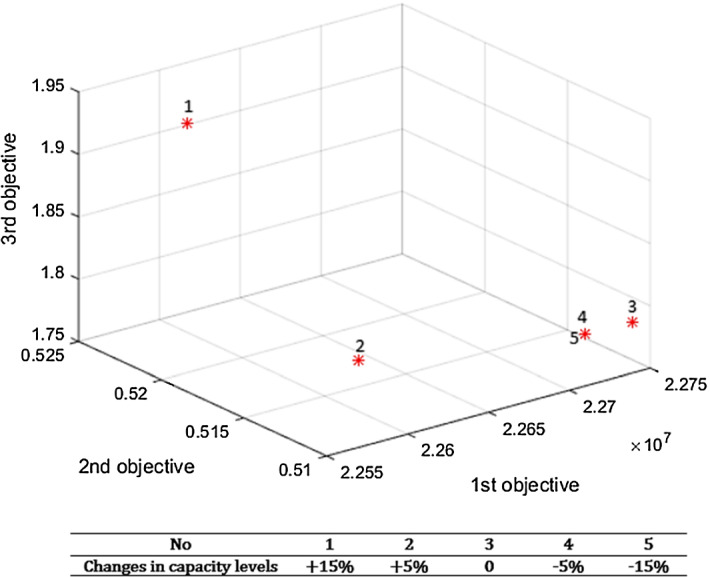
The impact of changes in capacity levels of opened RHFs on the objective’s value
Fig. 10.
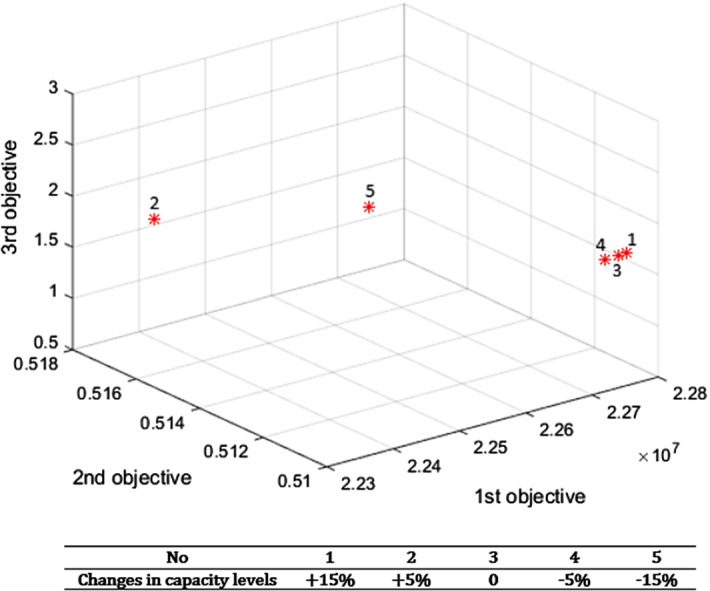
The impact of changes in capacity levels of opened DHFs on the objective’s value
To maximize the supply chain, social responsibility in response to the increased numbers of patients and disaster victims to healthcare facilities during the humanitarian crisis and decrease in the regional development rate, especially in less developed areas, the second OF has a tendency towards the more decentralized network as opposed to the cost OF that has a tendency towards network centralization. However, as it can be seen from Fig. 11, increasing the capacity to reduce the number of health service centers in the designed humanitarian HSN leads to a decrease in the overall public accessibility (a key dimension of social responsibility) to the health network.
Fig. 11.
The impact of increasing the capacity on accessibility (a key dimension of social responsibility) to health facilities
Discussion
As discussed in earlier sections, the need for a design of a HSN for humanitarian crisis management framework is felt in communities that lack of appropriate healthcare infrastructure. In this regard, this paper extends a novel multi-objective model for designing a three-tier HSN under uncertainty for Chaharmahal–Bakhtiari province which simultaneously considers efficiency, social responsibility, and network cost. The work by Haeri et al. (2020a) is the closest paper to the concerned problem of this study in terms of efficiency, in which an augmented form of DEA model is proposed and inserted into an integrated efficient–resilient model in order to minimize the inefficiency of each center. Nevertheless, the main difference is that they developed a common weights DEA for calculating efficiency, while in this study, a simultaneous DEA model is extended. In this study, in order to simultaneously consider both patterns of locations for PHFs, RHFs, and DHFs and the associated relative efficiencies of them at each location, the basic DEA model is modified by defining a new variable to allow for the efficiencies of all the facilities to be calculated in one linear program.
In terms of social responsibility, the closest paper to the concerned problem of this study is the work by Pishvaee et al. (2014), in which social responsibility measures are inserted into a multi-objective possibilistic programming model. However, the main difference is that they just considered medical service instead of the entire health service, including PHFs, RHFs, and DHFs. In this study, two measures of balanced development and job creation are incorporated into the design of the considered HSN to not only cope with the increased numbers of patients and disaster victims to healthcare facilities during the crisis but also increase the development rate of this province through improving population health.
Research implications
In this subsection, the roles of considering social responsibility, efficiency and uncertainty on the proposed humanitarian HSND are investigated.
Social responsibility analysis indicates that considering this measure increases the total cost of the humanitarian HSND, while it successfully contributes to job employment and development rate. This could be justified due to the fact that increasing the development rate and creating more job opportunities for specialists and other health workers in response to the increased numbers of patients and disaster victims during a humanitarian crisis such as the outbreak of the COVID-19 pandemic need more healthcare facilities to be opened in the candidate locations, which in turn increases the total cost of the proposed humanitarian HSND significantly.
Efficiency analysis suggests that taking this measure into account improves the efficiency of the proposed humanitarian HSND as well as the total cost of humanitarian HSND. In particular, delivering accessible, equitable and high-quality care among all people, especially in low- to middle-income communities, in support of humanitarian responses (e.g., COVID-19 response) need a decentralized network to be designed which contradicts the cost OF that has a tendency towards network centralization. Moreover, considering efficiency measure determines and ranks healthcare facilities belonging to the different tiers of the health system based on their performance and then the facilities with better performances can be used as benchmarks to improve inefficient facilities.
Uncertainty analysis reveals that contrary to MPFP models, the MPFRP models can efficiently specify the optimal value of confidence levels relevant to imprecise input parameters and flexible constraints and adjust the deviation of OF value from its expected performance. Thus, MPFRP models usually give higher performance than MPFP models do. In addition, among the MPSFP models, MPFRP II outperforms others in terms of the average and standard deviation of the OF value, as can be seen in Table 4.
Practice implications
In order to assist the health care and humanitarian crisis managers in possessing a good comprehension of the functionality of the extended model and its solution, the following insights are presented.
Inserting DEA measure into HSND for the promotion of health facilities, incorporating the concept of social responsibility into designing to create more value for the whole network, and considering the network costs are the significant matters that should get enough consideration while designing for HSN. First of all, the most important reason for inserting DEA measure into the proposed humanitarian HSND is to guarantee to deliver accessible, equitable, and high-quality care in support of humanitarian responses (e.g., COVID-19 response), especially in deprived areas that suffer from rather unresponsive and inefficient healthcare systems. In case of social responsibility, it should be noted that the most important reason for considering this measure is to mitigate not only the negative impacts of a health crisis such as the COVID-19 pandemic on the general public by providing more employment opportunities for health workers, but also the economic impact of the coronavirus pandemic through improving population health. In fact, healthier workers could reasonably be expected to produce more output per hour worked. Therefore, decision-makers should make a tradeoff between efficiency, social responsibility and the cost of opening new health facilities of any kind (either PHFs, RHFs, or DHFs).
In addition, conducting various sensitivity analyses on a number of critical parameters and analyzing the performance of MPFP in comparison with the MPFRP models indicated that compared with fuzzy programming models, MPFP for instance, robust models (i.e., MPFRP) can usually provide better performance. Amid the MPFRP models, MPSFRP II performs better than others in terms of cost, as can be observed in Table 4.
Social implications and policy implications
As mentioned before, unlike the extension of HSNs compared to 30 years ago, large group of people are partially covered or are not covered yet. A serious health crisis such as the outbreak of the COVID-19 pandemic can put an extra burden on health service providers on these communities and interrupted their access to support and assistance. The proposed humanitarian HSND model in this study is a step forward to not only mitigate health crises (e.g., the COVID-19 pandemic) or other potential humanitarian crisis, but also it will help the health-care policymakers to take responsible initiatives to increase the efficiency of healthcare facilities in providing accessible, equitable, and high-quality care among all people, especially in deprived areas that suffer from rather unresponsive and inefficient healthcare systems, and maximize sustainability in terms of maximizing social impacts.
Conclusion
With an increased number of humanitarian crisis situations, many communities are facing urgent challenges such as the unavailability of proper medical care. It is apparent that HSNs are much more extensive compared to a few decades ago; however, a large number of communities are not properly covered yet. Even though the healthcare service is available in other communities, the provided service is not that service that is necessarily needed, and there are still some supply gaps. In order to strengthen the health system response to the humanitarian crisis, especially in low- to middle-income communities, this paper extends a novel multi-objective model for designing a HSN under uncertainty which simultaneously considers efficiency, social responsibility, and network cost. To the best of the authors' knowledge, no previous paper has focused on simultaneous consideration of efficiency and social responsibility in humanitarian HSND, while this paper is the first to tackle such a problem. For efficiency, a modified form of DEA model is introduced and inserted into the extended model. Incorporating efficiency into humanitarian HSND can decrease the inefficiency of health service facilities and guarantee to deliver accessible, equitable, and high-quality care among all people, especially in deprived areas that suffer from rather unresponsive and inefficient healthcare systems. For social responsibility, two measures of job creation and balanced development are incorporated into the extended model. Considering the concept of social responsibility in humanitarian operations not only makes it possible to cope with the increased numbers of patients and disaster victims to healthcare facilities through creating more job opportunities for specialists and other health workers, but it also increases the development rate, especially in less developed areas as it increases production through improving population health. To protect the considered network from uncertainty, a novel MPFRP II approach is proposed, and then two other versions of this model (i.e., MPFRP I and MPFRP III) are developed and compared against the performance of MPFP models. Experiments indicate that contrary to MPFP models, the MPFRP models perform better in terms of social responsibility (72%), cost (8%), and efficiency (28%), and among MPFRP models, MPFRP II performs better in terms of cost OF.
Limitations
In this study, the resilience level of the designed network is not addressed while disregarding any short-term stoppage owing to internal or external sources of disruption in designing may bring about a considerable loss. Furthermore, social responsibility includes a wide variety of aspects that could be considered in humanitarian HSND, while this study has focused only on community involvement and development (Figs. 12, 13 and 14 and Table 12).
Avenues for future research
As the model of this paper is one of the first attempts in the context of humanitarian HSND, a number of directions can be proposed to enrich this issue. For example, addressing other health service facilities, applying exact algorithms to decrease the solving time, and taking other FP and PP methods into account for developing new robust fuzzy programming models are interesting future suggestions.
Appendix A
A range of DEA models has been extended that calculate efficiency in various ways. These largely are divided into two categories: (1) output-oriented models, (2) input-oriented models (Rezaee et al., 2018). Output oriented model maximizes the output while input is kept at a constant level, and the input-oriented model minimizes the input for a desired level of output to be obtained (Ozcan, 2014). Both output and input-oriented models seek to minimize the inputs, maximize the outputs and hence increase the efficiency. In general, output-oriented model is more related to strategy and planning, whereas input-oriented model closely focuses on managerial and operational issues (Cullinane et al., 2005).
Facility location is a branch of operations research, which is associated with locating/positioning at least a new facility among a number of existing facilities so as to optimize (maximize or minimize) at least one OF, for instance, waiting time, service, market shares, coverage, profit, cost, travel distance, and revenue (Farahani et al., 2010). In this study, we employ the concept of efficiency as defined by the conventional input-oriented DEA model as another objective for location modeling.
The below linear program is the conventional input-oriented DEA formulation for efficiency analysis:
| A.1 |
| A.2 |
| A.3 |
| A.4 |
where v and u represent vectors for the input and output weights, respectively. The typical DEA solution process includes sequentially solving the above model for each DMU. To simultaneously take into account both patterns of locations for facilities and their related efficiency scores at each location, the solution process for DEA needs to be improved to allow for the efficiency scores of all the DMUs to be measured in one linear program. To modify the conventional input-oriented DEA model for combining into the location/allocation models, a new variable () is defined as the level of inefficiency of (). Then, separating out in constraint (A.3) and combining , the following is achieved:
| A.5 |
Furthermore, since constraint (A.2) applies to , by substituting 1 for the weighted sum of outputs in (A.5), the below equation is achieved:
| A.6 |
With this adjustment to the constraint (A.3) and expanding this modification to the OF, the improved DEA formulation is now:
| A.7 |
Subject to
| A.8 |
| A.9 |
| A.10 |
| A.11 |
The above model is extended to solve for all DMUs simultaneously, as shown below in which uoa indicates the weight of the output a for DMUo and voe indicates the weight of the input e for DMUo.
| A.12 |
Subject to
| A.13 |
| A.14 |
| A.15 |
| A.16 |
OF (A.12) is the total inefficiency of all DMUs that the proposed simultaneous DEA minimizes it. Constraint (A.13) indicates the balanced collection of each part is equal to one. Constraint (A.14) shows is the weighted sum of the outputs of each DMU. Constraints (A.15) and (A.16) describe that each DMU's efficiency must be smaller than one. With respect to the abovementioned explanations, the formulation of the third OF is as below:
| A.17 |
The third OF, consisting of three terms, maximize the efficiencies of PHFs, RHFs, and DHFs, respectively.
Appendix B
Step 1 Take into account the below basic FP model in which soft (flexible) constraints are employed to the first and third constraints. Flexibility means that these constraints are free to be satisfied at a minimum degree individually, and the DMs could be involved in controlling the satisfaction degree of the constraints according to their subjective importance.
| B.1 |
In the above model (B.1), constraints 'coefficients are indicated through matrices A, B, S, T and C where C is a measure of health service facilities’ capacity; vectors y and x are considered as binary and positive variables, respectively; vector d reflects patient groups’ demand; vectors P, G and F indicate coefficients of first (cost), second (social responsibility) and third (DEA) OFs.
Step 2 To indicate the violation of soft constraints, two fuzzy numbers ( and ) can be used (Cadenas & Verdegay, 1997; Peidro et al., 2009). Therefore, model (B.1) can be rewritten as below:
| B.2 |
where parameters and adjust the minimum satisfaction level of flexible constraints.
Step 3 Three prominent points as and are defined to indicate the fuzzy triangular numbers of and which can be then de-fuzzified with respect to the fuzzy ranking method as below (Yager, 1979, 1981):
| B.3 |
| B.4 |
In which parameters and are regarded as lateral margins of and are calculated as presented in equations (B.5) and (B.6):
| B.5 |
| B.6 |
Step 4 With respect to equations (B.3) and (B.4), model (B.2) can be converted to its equivalent crisp model as below:
| B.7 |
In which the possible violation of each flexible constraint determined by the terms and .
Step 5 Since the elucidated method does not ensure to achieve optimal satisfaction degrees and as the flexible constraints enhance, more time-consuming experiments must be done to specify the value of the satisfaction degrees, the below robust FP method is presented in this step to eliminate these imperfections.
| B.8 |
Each objective of the model (B.8) has three terms in which the first terms indicate fixed opening cost, social responsibility, and DEA, respectively, while the total penalty cost of possible violation on first and third constraints are computed by the second and third terms. In other words, they adjust the feasibility robustness related to the soft constraints. In fact, the difference between the two extreme values of the right-hand side of flexible constraints is shown by the last two terms, which are stated as below:
| B.9 |
| B.10 |
Parameters and present penalty costs for each unit of violation on soft constraints. It is noteworthy that the value of satisfaction levels (i.e., and ) as two variables is optimized by the robust FP model. Consequently, repetitive subjective experiments by setting various values of and are not necessary. Additionally, owing to the augmentation of flexible constraints and their pertinent satisfaction level, the need to carry out time-consuming experiments is eliminated despite the basic FP model. Since the proposed model attempts to make a reasonable balance between the last two terms of each OF (the cost of robustness) and the first terms of each OF (the overall performance of the considered problem), it could be regarded as a realistic robust FP model.
Step 6 Multiplication of variables in the third constraint and the third term of (model B.8) results in non-linearity of the extended model. To convert model (B.8) into its equivalent linear model, Lemma 1 is described.
Lemma 1
By proposing as a non-negative auxiliary variable and adding constraints (B.11)–(B.14) into the MINLP model (B.8), it could be converted into its equivalent MILP one.
| B.11 |
| B.12 |
| B.13 |
| B.14 |
Proof
Constraints (B.11) and (B.14) compel to be equal to zero if Constraints (B.12) and (B.13) enforce to be equal to if . It should be noted that is a large number. According to the explained lemma, the robust FP model (B.8) can be rewritten as below:
| B.15 |
By adding some new terms in the OF, the provided robust FP has a good ability in controlling the feasibility robustness in contrast to the basic FP model, which results in more reliable and robust outcomes. Another positive feature of the robust FP model in comparison with traditional models is that it suitably optimizes the minimum satisfaction level of flexible constraints, which removes the necessity of time-consuming interactive experiments.
Step 7 An improved version of the robust FP model (B.16) is presented in this step to simultaneously deal with the flexible constraints and target value of goals.
| B.16 |
Similar to the robust FP model, the degree of feasibility robustness is controlled by the first and second terms of OF. An aspiration level (i.e., Φ) is also introduced to deal with flexibility on the target value of the goal. To adjust possible deviation of OF value from Φ, a new constraint along with the term is added in OF. The minimum satisfaction level connected to the flexibility of goal (i.e., η) is optimized by the third term of OF. In other words, optimality robustness is controlled by the third term. specifies the importance weight of the third term in contrast to the other terms of OF. The term is only related to deviation over the specified Φ. As a triangular fuzzy number, is related to the maximum violation of the added flexible constraint, which is defuzzified according to the fuzzy ranking method (Yager, 1979, 1981).
Step 8 Take into account the below basic MPFP model (Jimenez et al., 2007). It is assumed that vector d and coefficient matrix C in the first and third constraints, as well as vectors P, G and F in the OFs, are tainted with epistemic uncertainty. To model the imprecise parameters, triangular possibility distribution is utilized.
| B.17 |
As shown in the model (B.17), in order to model each OF, the expected value of the fuzzy number is utilized. The parameters and refer to the confidence level of constraints including uncertain parameters (. The satisfaction level of flexible constraints is indicated by the parameters and . DM should determine the above-mentioned parameters' value. However, as already mentioned, one of the shortcomings of the basic FP model is that time-consuming repetitive experiments are required to specify the suitable value of such parameters, and also, the optimality of the determined values cannot be assured by this method. In addition, the current OF, which is created with respect to the expected value, ignores the possible violation of OF due to parameters' uncertainty. The explained issues make unreliable consequences which may result in imposing high unexpected costs to DM.
Step 9 To eliminate the noted disadvantages in the previous step, a novel MPFRP model is extended according to the PP approach proposed by Pishvaee and Torabi (2010) and Jimenez et al. (2007).
Appendix C
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Abdorrrahman Haeri, Email: ahaeri@iust.ac.ir.
Seyyed-Mahdi Hosseini-Motlagh, Email: motlagh@iust.ac.ir.
Mohammad Reza Ghatreh Samani, Email: mr_samani@ind.iust.ac.ir.
Marziehsadat Rezaei, Email: m.rezaee90@yahoo.com.
References
- Acar M, Kaya O. A healthcare network design model with mobile hospitals for disaster preparedness: A case study for Istanbul earthquake. Transportation Research Part E: Logistics and Transportation Review. 2019;130:273–292. doi: 10.1016/j.tre.2019.09.007. [DOI] [Google Scholar]
- Behl A, Dutta P. Humanitarian supply chain management: A thematic literature review and future directions of research. Annals of Operations Research. 2019;283(1):1001–1044. doi: 10.1007/s10479-018-2806-2. [DOI] [Google Scholar]
- Cadenas JM, Verdegay JL. Using fuzzy numbers in linear programming. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics) 1997;27(6):1016–1022. doi: 10.1109/3477.650062. [DOI] [PubMed] [Google Scholar]
- Cheraghi S, Hosseini-Motlagh SM. Responsive and reliable injured-oriented blood supply chain for disaster relief: A real case study. Annals of Operations Research. 2018;291:1–39. [Google Scholar]
- Cullinane K, Ji P, Wang TF. The relationship between privatization and DEA estimates of efficiency in the container port industry. Journal of Economics and Business. 2005;57(5):433–462. doi: 10.1016/j.jeconbus.2005.02.007. [DOI] [Google Scholar]
- Dubey R, Altay N. Drivers of coordination in humanitarian relief supply chains. In: Kovács G, Spens K, Moshtari M, editors. The Palgrave handbook of humanitarian logistics and supply chain management. Palgrave Macmillan; 2018. pp. 297–325. [Google Scholar]
- Dubey R, Gunasekaran A, Papadopoulos T. Disaster relief operations: Past, present and future. Annals of Operations Research. 2019;283(1):1–8. doi: 10.1007/s10479-019-03440-7. [DOI] [Google Scholar]
- Eskandari-Khanghahi M, Tavakkoli-Moghaddam R, Taleizadeh AA, Amin SH. Designing and optimizing a sustainable supply chain network for a blood platelet bank under uncertainty. Engineering Applications of Artificial Intelligence. 2018;71:236–250. doi: 10.1016/j.engappai.2018.03.004. [DOI] [Google Scholar]
- Farahani RZ, SteadieSeifi M, Asgari N. Multiple criteria facility location problems: A survey. Applied Mathematical Modelling. 2010;34(7):1689–1709. doi: 10.1016/j.apm.2009.10.005. [DOI] [Google Scholar]
- Fazli-Khalaf M, Khalilpourazari S, Mohammadi M. Mixed robust possibilistic flexible chance constraint optimization model for emergency blood supply chain network design. Annals of Operations Research. 2019;283(1):1079–1109. doi: 10.1007/s10479-017-2729-3. [DOI] [Google Scholar]
- Gu J, Zhou Y, Das A, Moon I, Lee GM. Medical relief shelter location problem with patient severity under a limited relief budget. Computers and Industrial Engineering. 2018;125:720–728. doi: 10.1016/j.cie.2018.03.027. [DOI] [Google Scholar]
- Haeri A, Hosseini-Motlagh SM, Ghatreh Samani MR, Rezaei M. A mixed resilient–efficient approach toward blood supply chain network design. International Transactions in Operational Research. 2020;27(4):1962–2001. doi: 10.1111/itor.12714. [DOI] [Google Scholar]
- Haeri A, Motlagh SMH, Samani MRG, Rezaei MS. A bi-level programming approach for improving relief logistics operations: A real case in Kermanshah earthquake. Computers and Industrial Engineering. 2020;145:106532. doi: 10.1016/j.cie.2020.106532. [DOI] [Google Scholar]
- Hosseini-Motlagh SM, Samani MRG, Cheraghi S. Robust and stable flexible blood supply chain network design under motivational initiatives. Socio-Economic Planning Sciences. 2020;70:100725. doi: 10.1016/j.seps.2019.07.001. [DOI] [Google Scholar]
- Jimenez M, Arenas M, Bilbao A, Rodrı MV. Linear programming with fuzzy parameters: An interactive method resolution. European Journal of Operational Research. 2007;177(3):1599–1609. doi: 10.1016/j.ejor.2005.10.002. [DOI] [Google Scholar]
- Kamyabniya A, Lotfi MM, Cai H, Hosseininasab H, Yaghoubi S, Yih Y. A two-phase coordinated logistics planning approach to platelets provision in humanitarian relief operations. IISE Transactions. 2019;51(1):1–21. doi: 10.1080/24725854.2018.1479901. [DOI] [Google Scholar]
- Khalilpourazari S, Khamseh AA. Bi-objective emergency blood supply chain network design in earthquake considering earthquake magnitude: A comprehensive study with real world application. Annals of Operations Research. 2019;283(1):355–393. doi: 10.1007/s10479-017-2588-y. [DOI] [Google Scholar]
- Khalilpourazari S, Soltanzadeh S, Weber GW, Roy SK. Designing an efficient blood supply chain network in crisis: Neural learning, optimization and case study. Annals of Operations Research. 2020;289(1):123–152. doi: 10.1007/s10479-019-03437-2. [DOI] [Google Scholar]
- Kumar S, Panda TK, Behl A, Kumar A. A mindful path to the COVID-19 pandemic: An approach to promote physical distancing behavior. International Journal of Organizational Analysis. 2020 doi: 10.1108/IJOA-08-2020-2358. [DOI] [Google Scholar]
- Liu Y, Cui N, Zhang J. Integrated temporary facility location and casualty allocation planning for post-disaster humanitarian medical service. Transportation Research Part E: Logistics and Transportation Review. 2019;128:1–16. doi: 10.1016/j.tre.2019.05.008. [DOI] [Google Scholar]
- Mohamadi A, Yaghoubi S. A bi-objective stochastic model for emergency medical services network design with backup services for disasters under disruptions: An earthquake case study. International Journal of Disaster Risk Reduction. 2017;23:204–217. doi: 10.1016/j.ijdrr.2017.05.003. [DOI] [Google Scholar]
- Mousazadeh M, Torabi SA, Pishvaee MS. Health service network design under epistemic uncertainty. In: Kahraman C, Kaymak U, Yazici A, editors. Fuzzy logic in its 50th year. Springer; 2016. pp. 257–281. [Google Scholar]
- Mousazadeh M, Torabi SA, Pishvaee MS, Abolhassani F. Health service network design: A robust possibilistic approach. International Transactions in Operational Research. 2018;25(1):337–373. doi: 10.1111/itor.12417. [DOI] [Google Scholar]
- Mousazadeh M, Torabi SA, Pishvaee MS, Abolhassani F. Accessible, stable, and equitable health service network redesign: A robust mixed possibilistic-flexible approach. Transportation Research Part E: Logistics and Transportation Review. 2018;111:113–129. doi: 10.1016/j.tre.2018.01.006. [DOI] [Google Scholar]
- Ozcan YA. Performance measurement using data envelopment analysis (DEA) In: Ozcan YA, editor. Health care benchmarking and performance evaluation. Springer; 2014. pp. 15–47. [Google Scholar]
- Peidro D, Mula J, Poler R, Verdegay JL. Fuzzy optimization for supply chain planning under supply, demand and process uncertainties. Fuzzy Sets and Systems. 2009;160(18):2640–2657. doi: 10.1016/j.fss.2009.02.021. [DOI] [Google Scholar]
- Pishvaee MS, Razmi J, Torabi SA. An accelerated Benders decomposition algorithm for sustainable supply chain network design under uncertainty: A case study of medical needle and syringe supply chain. Transportation Research Part E: Logistics and Transportation Review. 2014;67:14–38. doi: 10.1016/j.tre.2014.04.001. [DOI] [Google Scholar]
- Pishvaee MS, Torabi SA. A possibilistic programming approach for closed-loop supply chain network design under uncertainty. Fuzzy Sets and Systems. 2010;161(20):2668–2683. doi: 10.1016/j.fss.2010.04.010. [DOI] [Google Scholar]
- Rezaee MS, Haeri A, Noori S. Using data envelopment analysis to evaluate the performances of food production companies based on EFQM's criteria and to present an improvement plan. International Journal of Business Excellence. 2018;14(2):256–274. doi: 10.1504/IJBEX.2018.089152. [DOI] [Google Scholar]
- Rezaei M, Haeri A. A heuristic method for choosing ‘virtual best’ DMUs to enhance discrimination power of augmented DEA model. Scientia Iranica. 2019 doi: 10.24200/sci.2019.52890.3009. [DOI] [Google Scholar]
- Salehi F, Mahootchi M, Husseini SMM. Developing a robust stochastic model for designing a blood supply chain network in a crisis: A possible earthquake in Tehran. Annals of Operations Research. 2019;283(1–2):679–703. doi: 10.1007/s10479-017-2533-0. [DOI] [Google Scholar]
- Samani MRG, Torabi SA, Hosseini-Motlagh SM. Integrated blood supply chain planning for disaster relief. International Journal of Disaster Risk Reduction. 2018;27:168–188. doi: 10.1016/j.ijdrr.2017.10.005. [DOI] [Google Scholar]
- Sharma B, Ramkumar M, Subramanian N, Malhotra B. Dynamic temporary blood facility location–allocation during and post-disaster periods. Annals of Operations Research. 2019;283(1):705–736. doi: 10.1007/s10479-017-2680-3. [DOI] [Google Scholar]
- Shibin KT, Dubey R, Gunasekaran A, Hazen B, Roubaud D, Gupta S, Foropon C. Examining sustainable supply chain management of SMEs using resource based view and institutional theory. Annals of Operations Research. 2020;290(1):301–326. doi: 10.1007/s10479-017-2706-x. [DOI] [Google Scholar]
- Tofighi S, Torabi SA, Mansouri SA. Humanitarian logistics network design under mixed uncertainty. European Journal of Operational Research. 2016;250(1):239–250. doi: 10.1016/j.ejor.2015.08.059. [DOI] [Google Scholar]
- Torabi SA, Hassini E. An interactive possibilistic programming approach for multiple objective supply chain master planning. Fuzzy Sets and Systems. 2008;159(2):193–214. doi: 10.1016/j.fss.2007.08.010. [DOI] [Google Scholar]
- Wamba, S. F. (2020). Humanitarian supply chain: A bibliometric analysis and future research directions. Annals of Operations Research, pp. 1–27.
- WHO . Macroeconomics and health: Investing in health for economic development: Report of the Commission on Macroeconomics and Health. WHO; 2001. pp. 202–202. [Google Scholar]
- WHO. (2020). Strengthening the health system response to COVID-19: technical guidance# 1: Maintaining the delivery of essential health care services while mobilizing the health workforce for the COVID-19 response. 18 April 2020 (No. WHO/EURO: 2020–669–40404–54161). World Health Organization. Regional Office for Europe.
- Xiang YT, Zhao YJ, Liu ZH, Li XH, Zhao N, Cheung T, Ng CH. The COVID-19 outbreak and psychiatric hospitals in China: Managing challenges through mental health service reform. International journal of biological sciences. 2020;16(10):1741. doi: 10.7150/ijbs.45072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yager, R. R. (1979). Ranking fuzzy subsets over the unit interval. In 1978 IEEE conference on decision and control including the 17th symposium on adaptive processes (pp. 1435–1437). IEEE.
- Yager RR. A procedure for ordering fuzzy subsets of the unit interval. Information sciences. 1981;24(2):143–161. doi: 10.1016/0020-0255(81)90017-7. [DOI] [Google Scholar]
- Zahiri B, Zhuang J, Mohammadi M. Toward an integrated sustainable-resilient supply chain: A pharmaceutical case study. Transportation Research Part E: Logistics and Transportation Review. 2017;103:109–142. doi: 10.1016/j.tre.2017.04.009. [DOI] [Google Scholar]
- Zarrinpoor N, Fallahnezhad MS, Pishvaee MS. Design of a reliable hierarchical location–allocation model under disruptions for health service networks: A two-stage robust approach. Computers and Industrial Engineering. 2017;109:130–150. doi: 10.1016/j.cie.2017.04.036. [DOI] [Google Scholar]
- Zhalechian M, Tavakkoli-Moghaddam R, Zahiri B, Mohammadi M. Sustainable design of a closed-loop location-routing-inventory supply chain network under mixed uncertainty. Transportation Research Part E: Logistics and Transportation Review. 2016;89:182–214. doi: 10.1016/j.tre.2016.02.011. [DOI] [Google Scholar]