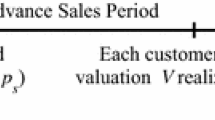Abstract
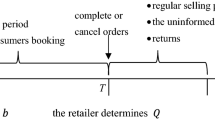
Advance selling with pre-orders has become a common practice in many industries. To encourage more consumers to purchasing in advance, retailers now try new forms of advance selling to allow consumers to complete their pre-orders after solving valuation uncertainty. Motivated by this emerging industry practice, this paper focuses on delay in payments from a retailer to consumers during the advance selling period and considers several pre-order strategies for the retailer, namely, free pre-order (FP), deposit pre-order (DP), and deposit expansion pre-order. Under the price commitment mechanism, we first derive not only the thresholds for pre-order strategies with stochastic demand and uncertain product valuation but also the retailer’s optimal price, quantity, and advance selling strategy, which are contingent on the relative size of the marginal cost and the lower bound of consumer valuation. Then, we find that the retailer should sell in advance even when the expected valuation is sufficiently low, or the marginal cost is relatively high. Besides, we reveal that the retailer is more likely to order a smaller quantity under the FP and DP strategies. Finally, we extend the model to a fixed pricing mechanism to further elucidate the retailer’s optimal decisions. By comparing these two pricing mechanisms, we find that, under certain conditions, the optimal pre-announced pricing strategy converges to the fixed pricing strategy.

Similar content being viewed by others
References
Aviv, Y., Levin, Y., & Nediak, M. (2009). Counteracting strategic consumer behavior in dynamic pricing systems. In S. Netessine & C. S. Tang (Eds.), Consumer-driven demand and operations management models (pp. 323–352). Springer.
Bickel, P. J., & Doksum, K. A. (1977). Mathematical statistics. Holden-Day.
Cachon, G. P. (2004). The allocation of inventory risk in a supply chain: Push, pull, and advance-purchase discount contracts. Management Science, 50(2), 222–238.
Cachon, G. P., & Feldman, P. (2017). Is advance selling desirable with competition? Marketing Science, 36(2), 214–231.
Chang, H. J., & Dye, C. Y. (2001). An inventory model for deteriorating items with partial backlogging and permissible delay in payments. International Journal of Systems Science, 32(3), 345–352.
Cheng, Y., Li, H., & Thorstenson, A. (2018). Advance selling with double marketing efforts in a newsvendor framework. Computers & Industrial Engineering. https://doi.org/10.1016/j.cie.2018.03.006.
Cho, S. H., & Tang, C. S. (2013). Advance selling in a supply chain under uncertain supply and demand. Manufacturing & Service Operations Management, 15(2), 305–319.
Das, D., Roy, A., & Kar, S. (2015). A multi-warehouse partial backlogging inventory model for deteriorating items under inflation when a delay in payment is permissible. Annals of Operations Research, 226(1), 133–162.
Davis, S., Gerstner, E., & Hagerty, M. (1995). Money back guarantees in retailing: Matching products to consumer tastes. Journal of Retailing, 71(1), 7–22.
Diabat, A., Taleizadeh, A. A., & Lashgari, M. (2017). A lot sizing model with partial downstream delayed payment, partial upstream advance payment, and partial backordering for deteriorating items. Journal of Manufacturing Systems, 45, 322–342.
Ghoreishi, M., Weber, G. W., & Mirzazadeh, A. (2015). An inventory model for non-instantaneous deteriorating items with partial backlogging, permissible delay in payments, inflation-and selling price-dependent demand and customer returns. Annals of Operations Research, 226(1), 221–238.
Goyal, S. K. (1985). Economic order quantity under conditions of permissible delay in payments. Journal of the Operational Research Society, 36(4), 335–338.
Guo, L. (2009). Service cancellation and competitive refund policy. Marketing Science, 28(5), 901–917.
He, B., Pan, W., & Yang, Y. (2019). Joint pricing and overbooking policy in a full payment presale mechanism of new products. International Transactions in Operational Research, 26(5), 1810–1827.
Huang, K. L., Kuo, C. W., & Shih, H. J. (2017). Advance selling with freebies and limited production capacity. Omega, 73, 18–28.
Jamal, A. M. M., Sarker, B. R., & Wang, S. (2000). Optimal payment time for a retailer under permitted delay of payment by the wholesaler. International Journal of Production Economics, 66(1), 59–66.
Lashgari, M., Taleizadeh, A. A., & Ahmadi, A. (2016). Partial up-stream advanced payment and partial down-stream delayed payment in a three-level supply chain. Annals of Operations Research, 238(1–2), 329–354.
Lashgari, M., Taleizadeh, A. A., & Sadjadi, S. J. (2017). Ordering policies for non-instantaneous deteriorating items under hybrid partial prepayment, partial delay payment and partial backordering. Journal of the Operational Research Society, 69(8), 1167–1196.
Li, Y., Xu, L., Choi, T. M., & Govindan, K. (2014). Optimal advance-selling strategy for fashionable products with opportunistic consumers returns. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 44(7), 938–952.
Lim, W. S., & Tang, C. S. (2013). Advance selling in the presence of speculators and forward-looking consumers. Production and Operations Management, 22(3), 571–587.
Liu, Q., & Van Ryzin, G. J. (2008). Strategic capacity rationing to induce early purchases. Management Science, 54(6), 1115–1131.
Ma, S., Li, G., Sethi, S. P., & Zhao, X. (2019). Advance selling in the presence of market power and risk-averse consumers. Decision Sciences, 50(1), 142–169.
Oh, J., & Su, X. (2018). Reservation policies in queues: Advance deposits, spot prices, and capacity allocation. Production and Operations Management, 27(4), 680–695.
Prasad, A., Stecke, K. E., & Zhao, X. (2011). Advance selling by a newsvendor retailer. Production and Operations Management, 20(1), 129–142.
Sana, S. S., & Chaudhuri, K. S. (2008). A deterministic EOQ model with delays in payments and price-discount offers. European Journal of Operational Research, 184(2), 509–533.
Shi, X., Dong, C., & Cheng, T. C. E. (2018). Does the buy-online-and-pick-up-in-store strategy with pre-orders benefit a retailer with the consideration of returns? International Journal of Production Economics, 206, 134–145.
Shugan, S. M., & Xie, J. (2000). Advance pricing of services and other implications of separating purchase and consumption. Journa of Service Research, 2(3), 227–239.
Shugan, S. M., & Xie, J. (2004). Advance selling for services. California Management Review, 46(3), 37–54.
Silver, E. A., Pyke, D. F., & Peterson, R. (1998). Inventory management and production planning and scheduling (Vol. 3, p. 30). Wiley.
Su, X., & Zhang, F. (2008). Strategic customer behavior, commitment, and supply chain performance. Management Science, 54(10), 1759–1773.
Su, X., & Zhang, F. (2009). On the value of commitment and availability guarantees when selling to strategic consumers. Management Science, 55(5), 713–726.
Taleizadeh, A. A. (2017). Lot-sizing model with advance payment pricing and disruption in supply under planned partial backordering. International Transactions in Operational Research, 24(4), 783–800.
Taleizadeh, A. A., Tavakoli, S., & San-José, L. A. (2018). A lot sizing model with advance payment and planned backordering. Annals of Operations Research,. https://doi.org/10.1007/s10479-018-2753-y.
Tang, C. S., Rajaram, K., Alptekinoğlu, A., & Ou, J. (2004). The benefits of advance booking discount programs: Model and analysis. Management Science, 50(4), 465–478.
Tian, Z., & Wang, Y. (2016). Advance selling with preorder-dependent customer valuation. Operations Research Letters, 44(4), 557–562.
Wei, M. M., & Zhang, F. (2018a). Recent research developments of strategic consumer behavior in operations management. Computers & Operations Research, 93, 166–176.
Wei, M. M., & Zhang, F. (2018b). Advance selling to strategic consumers: Preorder contingent production strategy with advance selling target. Production and Operations Management, 27(7), 1221–1235.
Xiao, L., Xu, M., Chen, Z., & Guan, X. (2019). Optimal pricing for advance selling with uncertain product quality and consumer fitness. Journal of the Operational Research Society,. https://doi.org/10.1080/01605682.2018.1489342.
Xie, J., & Gerstner, E. (2007). Service escape: Profiting from customer cancellations. Marketing Science, 26(1), 18–30.
Xie, J., & Shugan, S. M. (2001). Electronic tickets, smart cards, and online prepayments: When and how to advance sell. Marketing Science, 20(3), 219–243.
Zeng, C. (2013). Optimal advance selling strategy under price commitment. Pacific Economic Review, 18(2), 233–258.
Zhao, X., & Pang, Z. (2011). Profiting from demand uncertainty: pricing strategies in advance selling. Working Paper. SSRN. https://ssrn.com/abstract=1866765.
Zhao, X., Pang, Z., & Stecke, K. E. (2016). When does a retailer’ advance selling capability benefit manufacturer, retailer, or both? Production and Operations Management, 25(6), 1073–1087.
Zhao, X., & Stecke, K. E. (2010). Pre-orders for new to-be-released products considering consumer loss aversion. Production and Operations Management, 19(2), 198–215.
Zia, N. P., & Taleizadeh, A. A. (2015). A lot-sizing model with backordering under hybrid linked-to-order multiple advance payments and delayed payment. Transportation Research Part E: Logistics and Transportation Review, 82, 19–37.
Funding
Funding was provided by National Natural Science Foundation of China (Grant No. 72071188).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
1.1 Proof of Theorem 1
Note that strategic informed consumers are willing to pre-order new products if and only if they can get more expected utilities. From the expression (11), we can obtain \(X+\int _{X-em}^{p} F(v)\, dv\le p+\eta (h-p)+(e-1)m-\eta \int _{p}^{h} F(v)\, dv\). Because the left of inequality is increasing of X, we can get a maximum pre-order price \(X^{*}\) if all other factors are given. Therefore, the retailer would adopt this optimal pre-order price that induces all informed consumers to purchase with pre-orders.
1.2 Proof of Proposition 1
Let \(\vec {x}=(m^{*}, X^{*}, e^{*})\) be a local maximum solution for the problem of pure optimization which is expressed as follows:
For this model, its constraint is \((1-\eta )\int _p^h (v-p)f(v)\, dv+m-\int _{X-em}^{h} (V-X+em)f(v)\,dv\le 0\). Then it exists a vector \(\vec {r}=(r_1^{*}, r_2^{*}, r_3^{*}, r_4^{*})\), and its component \(r_i^{*}\ge 0, i=1, 2, 3, 4\). It makes \(\nabla f(\vec {x})-\sum _{i=1}^4 r_i^{*}\nabla g_i(\vec {x})=0\), \(r_i^{*}g_i(\vec {x})=0\). So we can obtain:
By mathematical calculation, it’s easy to get the results:
or
Substituting Eqs. (A.3), (A.4) into the total profit function, we have:
or
Intuitively, we can obtain \(\pi _1^{*}=\pi _2^{*}\) if \(c\le l\); otherwise, \(\pi _1^{*}>\pi _2^{*}\).
1.3 Proof of Proposition 3
Similar to Proof of Proposition 1, let \(\vec {x}=(m^{'*}, e^{'*})\) be a local maximum solution for the problem of pure optimization, its constraint is \((1-\eta )\int _p^h (v-p)f(v)\, dv+m^{'}-\int _{X^{*}-e^{'}m^{'}}^{h} (V-X^{*}+e^{'}m^{'})f(v)\,dv\le 0\). So we can obtain:
By mathematical calculation, we can obtain the results:
or
If \(e^{'*}m^{'*}=m^{*}\), and bring it to the constraint, we can obtain \(m^{'*}=p-c+\eta (h-p)-\eta \int _p^h F(v)\, dv-\int _c^p F(v)\, dv=m^{*}\), leading to \(e^{'*}=1\). So we neglect this case. If \(f(X^{*}-e^{'*}m^{'*})=0\), \(e^{'*}m^{'*}=m^{*}+c-l\) and bring it to the constraint, we can get \(m^{'*}=p-l+\eta (h-p)+(1-\eta )\int _p^h F(v)\, dv-\int _l^h F(v)\, dv\), and \(e^{'*}=\frac{p-l+\eta (h-p)+(1-\eta )\int _p^h F(v)\, dv-\int _c^h F(v)\, dv}{p-l+\eta (h-p)+(1-\eta )\int _p^h F(v)\, dv-\int _l^h F(v)\, dv}>1\) if and only if \(l<c\).
In summary, we can obtain optimal deposit and deposit expansion index under this setting with the condition \(l<c\), i.e., \(m^{'*}=p-l+\eta (h-p)+(1-\eta )\int _p^h F(v)\, dv-\int _l^h F(v)\, dv\), \(e^{'*}=\frac{p-l+\eta (h-p)+(1-\eta )\int _p^h F(v)\, dv-\int _c^h F(v)\, dv}{p-l+\eta (h-p)+(1-\eta )\int _p^h F(v)\, dv-\int _l^h F(v)\, dv}\). Substituting them into the profit function, corresponding optimal total profit under this scenario
It should be noted that optimal deposit expansion index \(e^{'*}\le 1\) if retailer sets the DEP price equal to the optimal pre-order price under DP strategy, i.e., \(X^{*}=m^{*}+l\). So we neglect this case.
1.4 Proof of Proposition 7
Let \(\vec {x}=(m_F^{*}, X_F^{*}, e_F^{*})\) be a local maximum solution for the problem of pure optimization, its constraint is \(\int _{X_F-e_Fm_F}^h F(v)\, dv-(e_F-1)m_F-\eta (h-X_F)-(1-\eta )\int _{X_F}^h F(v)\, dv\le 0\) for this model. Similarly, it exists a vector \(\vec {r}=(r_1^{*}, r_2^{*}, r_3^{*}, r_4^{*})\), and its component \(r_i^{*}\ge 0, i=1, 2, 3, 4\). It makes \(\nabla f(\vec {x})-\sum _{i=1}^4 r_i^{*}\nabla g_i(\vec {x})=0\), \(r_i^{*}g_i(\vec {x})=0\). Thus we have:
After calcution, we can obtain:
where
So we can get
or
At last, corresponding optimal profits are as follows:
or
Rights and permissions
About this article
Cite this article
Zhang, W., Yang, W. Optimal pre-order strategy with delay in payments. Ann Oper Res 305, 347–374 (2021). https://doi.org/10.1007/s10479-021-04207-9
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10479-021-04207-9