Skip to main content

Advertisement

Springer Nature Link
Log in

Reliability assessment of a multi-state distribution network under cost and spoilage considerations

  • Original Research
  • Published:
Annals of Operations Research Aims and scope Submit manuscript

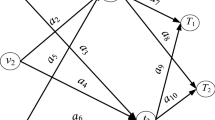
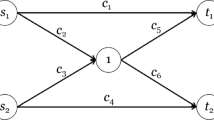
Abstract

The fundamental mission of a distribution network is to satisfy the customer demand by providing sufficient delivery capacity. However, the capacity of a distribution network is practically stochastic because of unexpected events, and moreover, the commodities may rot or be spoilt during delivery owing to inclement weather, traffic accidents, collisions, and so on, such that the intact commodity flow may not meet market demand. This paper focuses on the reliability of a multi-state distribution network (MSDN) with cost and spoilage characteristics, defined as the probability that the MSDN is able to distribute a sufficient quantity of goods to meet the market demand under delivery spoilage and budget limit considerations. A specific spoilage rate associated with each route is adopted to characterize the perishability of commodity flows, and the critical routes whose spoilage rate change has the biggest impact on network reliability are identified with the use of sensitivity analysis method. Apart from delivery cost, the cost involved with the disposal of spoilt goods is also incorporated into the reliability indicator. A minimal paths based algorithm is presented to calculate network reliability, together with an example to illustrate the procedure. A real fruit distribution network is accordingly discussed to demonstrate the utility of the algorithm and the managerial implication of network reliability.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

Abbreviations

MP:

Minimal path

MCV:

Minimal capacity vector

MSDN:

Multi-state distribution network

V :

Set of nodes

E :

Set of routes

(V, E):

An MSDN

m :

The number of routes in (V, E)

a i :

The ith route in (V, E)

s:

The single supplier which represents the single source node

λ :

The number of markets in (V, E)

tk :

The kth market in (V, E) which represent the sink node

π i :

The number of states owned by route ai

h ij :

The jth capacity of ai

H :

The maximal capacity vector of (V, E)

c i :

The cost per unit of used capacity through ai, i = 1, 2, …, m

C :

The cost per unit of spoilt commodity

w :

The capacity required for each unit of commodity

z k :

The number of MPs connecting the single source node s and sink node tk

MP k , j :

The MP connecting source s and sink tk

d k :

The demand of market tk

D :

Demand vector D = (d1, d2,…,dλ)

f k , j :

The normal flow through MPk,j

NF :

The normal-flow vector: \( (f_{{1,1}} , \ldots ,f_{{1,z_{1} }} ,f_{{2,1}} \ldots,f_{{2,z_{2} }} , \ldots,f_{{k,1}} , \ldots,f_{{k,z_{k} }} , \ldots,f_{{\lambda ,1}} , \ldots,f_{{\lambda ,z_{\lambda } }} ) \)

r i :

The spoilage rate of route ai

R :

Spoilage rate vector R = (r1, r2,…,rm)

r k , j :

The spoilage rate of MP MPk,j

o k , j :

The special flow through MPk,j

SF :

The special-flow vector: \( (o_{{1,1}} , \ldots ,o_{{1,z_{1} }} ,o_{{2,1}} , \ldots ,o_{{2,z_{2} }} , \ldots ,o_{{k,1}} , \ldots ,o_{{k,z_{k} }} , \ldots ,o_{{\lambda ,1}} , \ldots ,o_{{\lambda ,z_{\lambda } }} ) \)

x i :

The current capacity of ai for i = 1, 2,…, m

X :

X = (x1, x2,…,xm)

B :

Budget limit

R D , B , R :

Network reliability

(D, B, R)-MCV:

MCV that can meet the market demand vector D with the consideration of budget limit B and route spoilage pattern R

ΔH :

Sets of the feasible special-flow vectors under H

ΔX :

Sets of the feasible special-flow vectors under X

Ψ:

Set of feasible MCVs under (D, B, R)

[\( x \)]:

The smallest integer that is larger than or equal to x

References

  • Bai, G. H., Zuo, M. J., & Tian, Z. G. (2015). Ordering heuristics for reliability evaluation of multistate networks. IEEE Transactions on Reliability, 64(3), 1015–1023.

    Article  Google Scholar 

  • Chang, P. C. (2019). Reliability evaluation and big data analytics architecture for a stochastic flow network with time attribute. Annals of Operations Research. https://doi.org/10.1007/s10479-019-03427-4

    Article  Google Scholar 

  • Chopra, S. (2003). Designing the distribution network in a supply chain. Transportation Research Part E, 39(2), 123–140.

    Article  Google Scholar 

  • Forghani-elahabad, M., & Kagan, N. (2019). Reliability evaluation of a stochastic-flow network in terms of minimal paths with budget constraint. IIE Transactions, 51(5), 547–558.

    Google Scholar 

  • Forghani-elahabad, M., Kagan, N., & Mahdavi-Amiri, N. (2019). An MP-based approximation algorithm on reliability evaluation of multistate flow networks. Reliability Engineering and System Safety, 191, 106566.

    Article  Google Scholar 

  • Hao, Z. F., Yeh, W. C., Wang, J. G., Wang, G., & Sun, B. (2019). A quick inclusion-exclusion technique. Information Sciences, 486, 20–30.

    Article  Google Scholar 

  • Huang, C. F. (2019). Evaluation of system reliability for a stochastic delivery-flow distribution network with inventory. Annals of Operations Research, 277(1), 33–45.

    Article  Google Scholar 

  • Huang, C. F. (2020). System reliability for a multi-state distribution network with multiple terminals under stocks. Annals of Operations Research. https://doi.org/10.1007/s10479-020-03546-3

    Article  Google Scholar 

  • Jane, C. C., & Laih, Y. W. (2012). Evaluating cost and reliability integrated performance of stochastic logistics systems. Naval Research Logistics, 59(7), 577–586.

    Article  Google Scholar 

  • Lin, Y. K. (2002). Using minimal cuts to evaluate the system reliability of a stochastic-flow network with failures at nodes and arcs. Reliability Engineering & System Safety, 75(1), 41–46.

    Article  Google Scholar 

  • Lin, Y. K. (2004). Reliability of a stochastic-flow network with unreliable branches & nodes under budget constraints. IEEE Transactions on Reliability, 53(3), 381–387.

    Article  Google Scholar 

  • Lin, Y. K., & Chen, S. G. (2019). An efficient searching method for minimal path vectors in multi-state networks. Annals of Operations Research. https://doi.org/10.1007/s10479-019-03158-6

    Article  Google Scholar 

  • Lin, Y. K., Huang, C. F., & Liao, Y. C. (2019). Reliability of a stochastic intermodal logistics network under spoilage and time considerations. Annals of Operations Research, 277(1), 95–118.

    Article  Google Scholar 

  • Lin, Y. K., Huang, C. F., & Yeh, C. T. (2014). Network reliability with deteriorating product and production capacity through a multi-state delivery network. International Journal of Production Research, 52(22), 6681–6694.

    Article  Google Scholar 

  • Lin, Y. K., Nguyen, T. P., & Lu Yeng, L. C. (2018). Reliability evaluation of a multi-state air transportation network meeting multiple travel demands. Annals of Operations Research, 277, 63–82.

    Article  Google Scholar 

  • Lin, Y. K., & Yeh, C. T. (2010). Optimal carrier selection based on network reliability criterion for stochastic logistics networks. International Journal of Production Economics, 128, 510–517.

    Article  Google Scholar 

  • Lin, Y. K., Yeh, C. T., & Huang, C. F. (2013). Reliability evaluation of a stochastic-flow distribution network with delivery spoilage. Computers & Industrial Engineering, 66(2), 352–359.

    Article  Google Scholar 

  • Lin, Y. K., Yeh, C. T., & Huang, C. F. (2016). A simple algorithm to evaluate supply-chain reliability for brittle commodity logistics under production and delivery constraints. Annals of Operations Research, 244(1), 67–83.

    Article  Google Scholar 

  • Niu, Y. F., Gao, Z. Y., & Lam, W. H. K. (2017a). Evaluating the reliability of a stochastic distribution network in terms of minimal cuts. Transportation Research Part E, 100, 75–97.

    Article  Google Scholar 

  • Niu, Y. F., Gao, Z. Y., & Lam, W. H. K. (2017b). A new efficient algorithm for finding d-minimal cuts in multi-state networks. Reliability Engineering and System Safety, 166, 151–163.

    Article  Google Scholar 

  • Niu, Y. F., Lam, W. H. K., & Gao, Z. Y. (2014). An efficient algorithm for evaluating logistics network reliability subject to distribution cost. Transportation Research Part E, 67, 175–189.

    Article  Google Scholar 

  • Niu, Y. F., Wan, X. Y., Xu, X. Z., & Ding, D. (2020). Finding all multi-state minimal paths of a multi-state flow network via feasible circulations. Reliability Engineering and System Safety, 204, 107188.

    Article  Google Scholar 

  • Peng, P., Snyder, L. V., Lim, A., & Liu, Z. L. (2011). Reliable logistics networks design with facility disruptions. Transportation Research Part B, 45(8), 1190–1211.

    Article  Google Scholar 

  • Xu, X. Z., Niu, Y. F., & Song, Y. F. (2021). Computing the reliability of a stochastic distribution network subject to budget constraint”. Reliability Engineering and System Safety, 216, 107947.

    Article  Google Scholar 

  • Yeh, W. C. (2020). A new method for verifying d-MC candidates. Reliability Engineering and System Safety, 204, 107202.

    Article  Google Scholar 

  • Yeh, W. C., & Chu, T. C. (2018). A novel multi-distribution multi-state flow network and its reliability optimization problem. Reliability Engineering and System Safety, 176, 209–217.

    Article  Google Scholar 

  • Zuo, M. J., Tian, Z. G., & Huang, H. Z. (2007). An efficient method for reliability evaluation of multistate networks given all minimal path vectors. IIE Transactions, 39(8), 811–817.

    Article  Google Scholar 

Download references

Funding

This work is jointly supported by the National Natural Science Foundation of China (Grant Nos. 71601072, 61872126), the Scientific and Technological Research Program of Chongqing Municipal Education Commission (Grant Nos. KJQN201900634, KJQN201900649), the Doctoral Project of Chongqing Federation of Social Science Circles (Grant No. 2019BS064), and the Planning Project of Human Social Science of Chongqing Municipal Education Commission (Grant Nos. 20SKGH069, 20SKGH061, 20SKGH063).

Author information

Authors and Affiliations

  1. School of Economics and Management, Chongqing University of Posts and Telecommunications, Chongqing, 400065, China

    Yi-Feng Niu, Can He & De-Qiang Fu

Authors
  1. Yi-Feng Niu
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Can He
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. De-Qiang Fu
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Yi-Feng Niu.

Ethics declarations

Conflict of interest

The authors declare that they have no conflicts of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Niu, YF., He, C. & Fu, DQ. Reliability assessment of a multi-state distribution network under cost and spoilage considerations. Ann Oper Res 309, 189–208 (2022). https://doi.org/10.1007/s10479-021-04322-7

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10479-021-04322-7

Keywords