Abstract
Reverse factoring, a financial scheme in which established retailers facilitate financing for suppliers, is becoming an increasingly important tool in the industry. Normally, an SME supplier, a core retailer and a bank participate in the reverse factoring scheme. A three-level Stackelberg game is proposed in this study to investigate the interaction of the participants. The closed-form equilibria of the retailer’s replenishment decision, the supplier’s payment term decision and the bank’s financing decision are derived from the theoretical model. To our knowledge, this study is the first attempt which takes banks into account and endogenises their interest rates in the modelling of reverse factoring. The reverse factoring scheme is compared with commercial loans and traditional factoring. Compared to commercial loans, the introduction of factoring can lower credit risk, but fraud risk still exists. Reverse factoring solves this fraud problem and further decreases the financing cost for the supplier. Consequently, reverse factoring benefits the retailer through a significantly increased payment extension granted by the supplier. The numerical results also indicate that the utility of the bank significantly improves by 8–50% under varying levels of default risk compared with traditional factoring. Our study provides incentives and guidelines for supply chain participants to adopt such schemes when faced with capital constraints and the credit risk of the supplier.









Similar content being viewed by others
Notes
http://www.stats.gov.cn/english/PressRelease/202002/t20200204_1725014.html (accessed 30 August 2020).
https://fci.nl/en/annual-review (accessed 30 August 2020).
https://www.worldbank.org/en/topic/smefinance (accessed 15 May 2021).
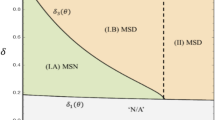
Subscript BU/BL/BLL here represents the three circumstances of the financial constraints: without financial constraints, with financial constraints but can meet the minimum ordering request and with financial constraints and fails to meet the minimum ordering request
http://bank.pingan.com/gongsi/rongzi/guonei/fanxiangbaoli.shtml (accessed 30 August 2020).
http://english.www.gov.cn/policies/policywatch/202002/21/content_WS5e4f4bcbc6d0595e03c21296.html (accessed 30 August 2020).
The equilibrium in the benchmark model here is under the condition of no capital constraint. The interest rate α in the benchmark model is an assumption instead of the equilibrium result. To provide a clear comparison, it is presented here together with the equilibrium results of the other two models.
With the current parameter settings, the capital of the supplier to support the optimal order quantity is equal to (\(c{q}_{BU}+w{q}_{BU}{T}_{BU}\) α) = 426.5625. When the supplier’s controlling capital L is lower than 426.5625, the supplier cannot support the optimal decisions and a capital constraint exists. The minimum order quantity of the retailer would be = b-w(b-a) = 750. To support the production, the funds of the supplier need to be above 375. If L is lower than 375, the supplier fails to afford the minimum order quantity from retailers.
References
Babich, V., & Kouvelis, P. (2018). Introduction to the Special Issue on Research at the Interface of Finance, Operations, and Risk Management (iFORM): Recent Contributions and Future Directions. Manufacturing & Service Operations Management, 20(1), 1–18. https://doi.org/10.1287/msom.2018.0706
Brealey, R. A., Myers, S. C., & Allen, F. (2010). Principles of Corporate Finance, Concise. McGraw-Hill Education.
Buzacott, J. A., & Zhang, R. Q. (2004). Inventory Management with Asset-Based Financing. Management Science, 50(9), 1274–1292. https://doi.org/10.1287/mnsc.1040.0278
Cachon, G. P., & Netessine, S. (2006). Game Theory in Supply Chain Analysis. Models, Methods, and Applications for Innovative Decision Making (pp. 200–233, INFORMS TutORials in Operations Research): INFORMS, https://doi.org/10.1287/educ.1063.0023
Chen, J., Zhou, Y.-W., & Zhong, Y. (2017). A pricing/ordering model for a dyadic supply chain with buyback guarantee financing and fairness concerns. International Journal of Production Research, 55(18), 5287–5304. https://doi.org/10.1080/00207543.2017.1308571
Chen, X., Cai, G., & Song, J.-S. (2019). The Cash Flow Advantages of 3PLs as Supply Chain Orchestrators. Manufacturing & Service Operations Management, 21(2), 435–451. https://doi.org/10.1287/msom.2017.0667
Chen, X., & Wang, A. (2012). Trade credit contract with limited liability in the supply chain with budget constraints. Annals of Operations Research, 196(1), 153–165. https://doi.org/10.1007/s10479-012-1119-0
Chen, Y., Chung, S.-H., & Guo, S. (2020). Franchising contracts in fashion supply chain operations: Models, practices, and real case study. Annals of Operations Research, 291(1), 83–128. https://doi.org/10.1007/s10479-018-2998-5
Dada, M., & Hu, Q. (2008). Financing newsvendor inventory. Operations Research Letters, 36(5), 569–573. https://doi.org/10.1016/j.orl.2008.06.004
Dello Iacono, U., Reindorp, M., & Dellaert, N. (2015). Market adoption of reverse factoring. International Journal of Physical Distribution & Logistics Management, 45(3), 286–308. https://doi.org/10.1108/ijpdlm-10-2013-0258
Duan, C., Deng, C., Gharaei, A., Wu, J., & Wang, B. (2018). Selective maintenance scheduling under stochastic maintenance quality with multiple maintenance actions. International Journal of Production Research, 56(23), 7160–7178. https://doi.org/10.1080/00207543.2018.1436789
Du, R., Banerjee, A., & Kim, S.-L. (2013). Coordination of two-echelon supply chains using wholesale price discount and credit option. International Journal of Production Economics, 143(2), 327–334. https://doi.org/10.1016/j.ijpe.2011.12.017
Fabbri, D., & Klapper, L. (2008). Market Power and the Matching of Trade Credit Terms. The World Bank, http://hdl.handle.net/10986/6913.
Fabbri, D., & Klapper, L. F. (2016). Bargaining power and trade credit. Journal of Corporate Finance, 41, 66–80. https://doi.org/10.1016/j.jcorpfin.2016.07.001
Gharaei, A., Hoseini Shekarabi, S. A., & Karimi, M. (2020a). Modelling and optimal lot-sizing of the replenishments in constrained, multi-product and bi-objective EPQ models with defective products: Generalised Cross Decomposition. International Journal of Systems Science: Operations & Logistics, 7(3), 262–274. https://doi.org/10.1080/23302674.2019.1574364
Gharaei, A., Hoseini Shekarabi, S. A., Karimi, M., Pourjavad, E., & Amjadian, A. (2019a). An integrated stochastic EPQ model under quality and green policies: Generalised cross decomposition under the separability approach. International Journal of Systems Science: Operations & Logistics. https://doi.org/10.1080/23302674.2019.1656296
Gharaei, A., Karimi, M., & Hoseini Shekarabi, S. A. (2020b). Joint Economic Lot-sizing in Multi-product Multi-level Integrated Supply Chains: Generalized Benders Decomposition. International Journal of Systems Science: Operations & Logistics, 7(4), 309–325. https://doi.org/10.1080/23302674.2019.1585595
Gharaei, A., Karimi, M., & Hoseini Shekarabi, S. A. (2019b). An integrated multi-product, multi-buyer supply chain under penalty, green, and quality control polices and a vendor managed inventory with consignment stock agreement: The outer approximation with equality relaxation and augmented penalty algorithm. Applied Mathematical Modelling, 69, 223–254. https://doi.org/10.1016/j.apm.2018.11.035
Grüter, R., & Wuttke, D. A. (2017). Option matters: Valuing reverse factoring. International Journal of Production Research, 55(22), 6608–6623. https://doi.org/10.1080/00207543.2017.1330564
Hoseini Shekarabi, S. A., Gharaei, A., & Karimi, M. (2019). Modelling and optimal lot-sizing of integrated multi-level multi-wholesaler supply chains under the shortage and limited warehouse space: Generalised outer approximation. International Journal of Systems Science: Operations & Logistics, 6(3), 237–257. https://doi.org/10.1080/23302674.2018.1435835
Huang, J., & Chen, Z. (2020). Optimal risk asset allocation of a loss-averse bank with partial information under inflation risk. Finance Research Letters. https://doi.org/10.1016/j.frl.2020.101513
Huang, J., Yang, W., & Tu, Y. (2020). Financing mode decision in a supply chain with financial constraint. International Journal of Production Economics, 220, 107441. https://doi.org/10.1016/j.ijpe.2019.07.014
Jaggi, P. C., Aggarwal, K., & Goel, S. (2007). Retailer’s optimal ordering policy under two stage credit financing. AMO - Advanced Modeling and Optimization, 9, 67–80.
Jing, B., Chen, X., & Cai, G. G. (2012). Equilibrium Financing in a Distribution Channel with Capital Constraint. Production and Operations Management, 21(6), 1090–1101. https://doi.org/10.1111/j.1937-5956.2012.01328.x
Kahneman, D., & Tversky, A. (1979). Prospect Theory: An Analysis of Decision under Risk. Econometrica, 47(2), 263–291. https://doi.org/10.2307/1914185
Klapper, L. (2006). The role of factoring for financing small and medium enterprises. Journal of Banking & Finance, 30(11), 3111–3130. https://doi.org/10.1016/j.jbankfin.2006.05.001
Lekkakos, S. D., & Serrano, A. (2016). Supply chain finance for small and medium sized enterprises—the case of reverse factoring. International Journal of Physical Distribution & Logistics Management. https://doi.org/10.1108/IJPDLM-07-2014-0165
Liebl, J., Hartmann, E., & Feisel, E. (2016). Reverse factoring in the supply chain: Objectives, antecedents and implementation barriers. International Journal of Physical Distribution & Logistics Management, 46(4), 393–413. https://doi.org/10.1108/ijpdlm-08-2014-0171
Owens, J. V., & Wilhelm, L. (2017). Alternative Data Transforming SME Finance. Working Paper, http://documents.worldbank.org/curated/en/701331497329509915/Alternative-data-transforming-SME-finance
Schwartz, R. A. (1974). An Economic Model of Trade Credit. Journal of Financial and Quantitative Analysis, 9(4), 643–657. https://doi.org/10.2307/2329765
Seifert, D., Seifert, R. W., & Protopappa-Sieke, M. (2013). A review of trade credit literature: Opportunities for research in operations. European Journal of Operational Research, 231(2), 245–256. https://doi.org/10.1016/j.ejor.2013.03.016
Seifert, R. W., & Seifert, D. (2011). Financing the Chain. International Commerce Review, 10(1), 32–44. https://doi.org/10.1007/s12146-011-0065-0
Tanaka, T., Camerer, C. F., & Nguyen, Q. (2010). Risk and Time Preferences: Linking Experimental and Household Survey Data from Vietnam. American Economic Review, 100(1), 557–571. https://doi.org/10.1257/aer.100.1.557
Tanrisever, F., Cetinay, H., Reindorp, M., & Fransoo, J. (2012). Value of Reverse Factoring in Multi-stage Supply Chains. SSRN Electronic Journal. https://doi.org/10.2139/ssrn.2183991
Tunca, T. I., & Zhu, W. (2018). Buyer Intermediation in Supplier Finance. Management Science, 64(12), 5631–5650. https://doi.org/10.1287/mnsc.2017.2863
van der Vliet, K., Reindorp, M. J., & Fransoo, J. C. (2015). The price of reverse factoring: Financing rates versus payment delays. European Journal of Operational Research, 242(3), 842–853. https://doi.org/10.1016/j.ejor.2014.10.052
Vörös, J. (1999). On the risk-based aggregate planning for seasonal products. International Journal of Production Economics, 59(1), 195–201. https://doi.org/10.1016/S0925-5273(98)00100-5
Wanke, P. F. (2008). The uniform distribution as a first practical approach to new product inventory management. International Journal of Production Economics, 114(2), 811–819. https://doi.org/10.1016/j.ijpe.2008.04.004
Wu, Y., Wang, Y., Xu, X., & Chen, X. (2019). Collect payment early, late, or through a third party’s reverse factoring in a supply chain. International Journal of Production Economics, 218, 245–259. https://doi.org/10.1016/j.ijpe.2019.04.040
Xu, X., Chen, X., Jia, F., Brown, S., Gong, Y., & Xu, Y. (2018). Supply chain finance: A systematic literature review and bibliometric analysis. International Journal of Production Economics, 204, 160–173. https://doi.org/10.1016/j.ijpe.2018.08.003
Yan, N., He, X., & Liu, Y. (2019). Financing the capital-constrained supply chain with loss aversion: Supplier finance vs. supplier investment. Omega, 88, 162–178. https://doi.org/10.1016/j.omega.2018.08.003
Yin, S., Nishi, T., & Zhang, G. (2016). A game theoretic model for coordination of single manufacturer and multiple suppliers with quality variations under uncertain demands. International Journal of Systems Science: Operations & Logistics, 3(2), 79–91. https://doi.org/10.1080/23302674.2015.1050079
Zhang, T., Choi, T.-M., & Zhu, X. (2018). Optimal green product’s pricing and level of sustainability in supply chains: Effects of information and coordination. Annals of Operations Research. https://doi.org/10.1007/s10479-018-3084-8
Zhao, Y., Choi, T.-M., Cheng, T. C. E., & Wang, S. (2017). Mean-risk analysis of wholesale price contracts with stochastic price-dependent demand. Annals of Operations Research, 257(1), 491–518. https://doi.org/10.1007/s10479-014-1689-0
Zhu, Y., Zhou, L., Xie, C., Wang, G.-J., & Nguyen, T. V. (2019). Forecasting SMEs’ credit risk in supply chain finance with an enhanced hybrid ensemble machine learning approach. International Journal of Production Economics, 211, 22–33. https://doi.org/10.1016/j.ijpe.2019.01.032
Acknowledgements
The authors would like to express their gratitude to the guest editor and two anonymous referees for their valuable comments and suggestions which contributed to a significant improvement of the original version of this paper. The authors would also like to thank Xiaoyi Mu for his helpful comments and suggestions regarding this work. Financial support from the National Natural Science Foundation of China (Grant No. 71804188) and the Science Foundation of China University of Petroleum, Beijing (Grant No. 2462020YXZZ038) are gratefully acknowledged.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendices
Appendix A1: Proof of Proposition 1.
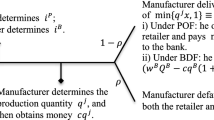
We use the method of backward induction to obtain the optimal solution. First, the retailer decides its own order quantity \({q}_{B}\) based on the existing payment term \({T}_{B}\). As f(x) follows a uniform distribution U[a, b], \(f(x)=\frac{1}{b-a}\). At the same time, the retail price per unit p is normalised to 1, that is, p = 1.
Equation (1) can be rewritten as
Taking the first derivative of \({q}_{B}\) in Eq. (1), we have:
Taking the second derivative of \({q}_{B}\) in Eq. (1), we have:
As \(\frac{{d}^{2}{\pi }_{B}^{r}}{d{q}_{B}^{2}}=-\frac{1}{b-a}\) <0, the objective function \({\pi }_{B}^{r}\) is concave in \({q}_{B}\).
-
A.
When a supplier has no financial constraint, we can obtain the optimal solution of \({q}_{B}\)
by solving \(\frac{{d\pi }_{B}^{r}}{{dq}_{B}}=0\):
To make the problem nontrivial, we suppose T≧ 0. Under this condition, the minimum order quantity of the retailer is qbmin=b–w(b–a)≦ b–w(1–TBθ)(b–a). The retailer will choose the minimum order quantity when the supplier does not grant it any payment term, that is, \({T}_{B}\)=0.
-
B.
When the supplier has a financial constraint but \({cq}_{B}^{min}\)<L, i.e., c(b–w(b–a)) < L, the supplier is able to meet the minimum order quantity of the retailer. The supplier can still set up a \({T}_{B}\)>0 to stimulate the demand from the retailer. The optimal solution is \({q}_{B}^{*}\)=\({q}_{BL}=\) b–w(1–\({T}_{B}\) θ)(b–a), obtained by solving \(\frac{{d\pi }_{B}^{r}}{{dq}_{B}}=0\).
-
C.
When a supplier has a financial constraint and \({cq}_{B}^{min}\)>L, that is, c(b–w(b–a)) > L, the supplier is unable to meet the minimum order quantity \({q}_{B}^{min}\) of the retailer. The order quantity that the supplier can meet is no more than L/c. It is obvious that the retailer’s profit is increasing in [0, L/c]. Hence, the order quantity of the retailer in this circumstance is \({q}_{B}^{*}\)=\({q}_{BLL}\)=L/c, and \({q}_{BLL}\)<\({q}_{B}^{min}\)<\({q}_{BL}\).
Second, the supplier decides its payment term for the retailer while considering the impact of its decision on the retailer.
Taking the first derivative of \({T}_{B}\) in Eq. (2), we have:
Taking the second derivative of \({T}_{B}\) in Eq. (2), we have:
As \(\frac{{d}^{2}{\pi }_{B}^{s}}{d{T}_{B}^{2}}=\frac{{dq}_{B}}{{dT}_{B}}*(-2w\alpha )<0\), the objective function \({\pi }_{B}^{s}\) is concave in \({T}_{B}\).
-
A.
When there is no financial constraint, solving \(\frac{{d\pi }_{B}^{s}}{{dT}_{B}}=0\) gives us:
At the same time, the order quantity of the retailer is \(q_{B}^{*} = q_{BU} = b - w\left( {1 - T_{BU} \theta } \right)\left( {b - a} \right)\).
For \({T}_{B}^{*}\geqq 0\), the condition \(\alpha \leqq \frac{(b-a)\theta (w-c)}{b-(b-a)w}\) should be met. This implies that the interest rate on commercial loans cannot be too high; otherwise, it will be too costly for the supplier to set up any credit term.
-
B.
When there is a financial constraint but c \({q}_{B}^{min}\)<L, i.e., c(b–w(b–a)) < L, the optimal solution remains as \({q}_{B}^{*}\)=\({q}_{BL}\)=b–w(1–\({T}_{B}\) θ)(b–a); however, the supplier does not have enough funds to afford the original optimal payment term \({T}_{BU}=\frac{w-c}{2w\alpha }+\frac{1}{2\theta }-\frac{b}{(b-a)*2w\theta }\). We denote the maximum payment term that the supplier can afford in this circumstance as TBL. In this case, \({T}_{BL}<{T}_{BU}\). It is obvious that the supplier’s profit is increasing in [0, TBL]. Hence, the optimal payment term \({T}_{B}^{*}\) in this circumstance would be TBL.
The production cost of the supplier is equal to cqBL + wqBLTBLα. By solving cqBL + wqBLTBLα = L, we have:
At the same time, the order quantity of the retailer is \({q}_{B}^{*}\)=qBL=b–w(1–\({T}_{BL}\) θ)(b–a).
In addition, \({q}_{B}^{*}\)=qBL=b–w(1–\({T}_{BL}\) θ)(b–a) < b–w(1–\({T}_{BU}\) θ)(b–a) = qBU.
-
C.
When there is a financial constraint and \({cq}_{B}^{min}\)>L, i.e., c(b–w(b–a)) > L, the supplier is unable to meet the minimum order quantity of the retailer and \({q}_{B}^{*}\)=qBLL < \({q}_{B}^{min}\)<qBL<qBU. There is no reason for the supplier to set up any payment term to stimulate the order quantity. Hence, we have \(T_{B}^{*} = T_{BLL} = 0,\) and \({T}_{BLL}\)<\({T}_{BL}\)<\({T}_{BU}\).
Appendix A2: Proof of Proposition 2
We use the method of backward induction to obtain the optimal solution. First, the retailer decides on its order quantity based on the payment term \({T}_{TF}\). In this circumstance, there is no financial constraint. Similar to the proof of proposition 1, by solving \(\frac{{d\pi }_{TF}^{r}}{{dq}_{TF}}\)=0, we obtain the optimal solution q*TF(TTF)=b–w(1–TTFθ)(b–a).
Next, by solving \(\frac{{d\pi }_{TF}^{s}}{{dT}_{TF}}=0\), we have: \(T_{TF}^{*} = \frac{w - c}{{2wr_{TF}^{*} }} + \frac{1}{2\theta } - \frac{b}{{\left( {b - a} \right)*2w\theta }}\).
Since we assume \(T_{TF}^{*}\)≧0, the condition \(r_{TF} { \leqq }\frac{{\left( {b - a} \right)\theta \left( {w - c} \right)}}{{b - \left( {b - a} \right)w}}\) should be met.
Finally, the bank decides on \({r}_{TF}\). Taking the first derivative of Eq. (3), we have:
It can be proved that there exists one point x. \(\frac{d{ lnU( \pi }_{TF}^{b})}{dr}\)>0 when \({r}_{TF}\) is inside [0, x], \(\frac{d{ lnU( \pi }_{TF}^{b})}{dr}\)<0 when \({r}_{TF}\) is inside [x,\(\frac{(b-a)\theta (w-c)}{b-(b-a)w}\)], under the condition of \(\frac{(b-a)(w-c){/[\eta /(\eta +\lambda -\lambda \eta )]}^\frac{1}{2}}{b-(b-a)w}>1\).
By solving \(\frac{d{ lnU( \pi }_{TF}^{b})}{dr}=\) 0, we have
where.
It can be proved that \({0\leqq r}_{TF}^{*}\leqq \frac{(b-a)\theta (w-c)}{b-(b-a)w}\) at the current condition. Therefore, \({r}_{TF}^{*}\) is the equilibrium result.
Similar to the proof of proposition 1, we can obtain:
“Appendix A3”: Proof of Proposition 4
As \(\eta \)<1 and \(\lambda \)<1, it is obvious that \(\eta /(\eta +\lambda -\lambda \eta )\) <1.
As \(\eta /(\eta +\lambda -\lambda \eta )\)<1, it is obvious that \({r}_{TF}^{*}\)>\({r}_{RF}^{*}\).

Appendix A4: Proof of Proposition 5
qBLL < qBL < qBU and TBLL < TBL < TBU is already proved in proposition 1.
B. As TBU < TRF*, qBU = b–w(1–TBUθ)(b–a) < b–w(1–TRF*θ)(b–a) = qRF*.
As α>\({r}_{RF}^{*},\) TBU < \({T}_{RF}^{*}\), and qBU\({<q}_{RF}^{*}\), we have.
It is obvious that \({\pi }_{B}^{s}\) is increasing in [0, \({T}_{BU}\)]. Hence, \({\pi }_{BU}^{s*}\)>\({\pi }_{BL}^{s*}\)>\({\pi }_{BLL}^{s*}\).

It is obvious that \({\pi }_{B}^{r}\) is increasing in [0, \({q}_{BU}\)]. Hence, \({\pi }_{BU}^{r*}\)>\({\pi }_{BL}^{r*}\)>\({\pi }_{BLL}^{r*}\).
Rights and permissions
About this article
Cite this article
Zhu, L., Ou, Y. Enhance financing for small- and medium-sized suppliers with reverse factoring: a game theoretical analysis. Ann Oper Res 331, 159–187 (2023). https://doi.org/10.1007/s10479-021-04361-0
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10479-021-04361-0