Skip to main content
Springer Nature Link
Log in

Average lexicographic efficiency decomposition in two-stage data envelopment analysis: an application to China’s regional high-tech innovation systems

  • Original Research
  • Published:
Annals of Operations Research Aims and scope Submit manuscript

Abstract

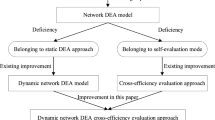
This paper proposes a lexicographic decomposition strategy for the two-stage network DEA model. Instead of assigning a priority over the two component stages, our proposed approach employs a lexicographic algorithm in such a way that the system efficiencies of the DMUs are lexicographically computed for each of their possible sequences while maintaining the efficiencies of those units already investigated unchanged. In particular, the system efficiency and the two component efficiencies can be uniquely determined under our proposed decomposition approach. Besides, prior to implement the proposed lexicographic evaluation procedure, we also highlight a potential infeasibility problem arising from the normalization constraint, and develop a modified iterative approach that facilitates us to guarantee a feasible search procedure. Finally, we use a numerical example to illustrate the effectiveness of the proposed approach, and conduct an empirical study to analyze China’s regional high-tech innovation systems for the period of 12th Five-Year Plan (2011–2015).

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

Notes

  1. In order to guarantee the uniqueness of the multipliers used for calculating the component efficiencies, Kao and Liu (2019) maximized the aggregate efficiency of all DMUs for the arbitrary most important division while maintaining the aggregate system efficiency of the other DMUs unchanged. However, such a practice cannot guarantee unique efficiency decomposition.

  2. Herein, it is worth noting that there are generally two strategies to decompose the system efficiency under the two-stage production structure, namely the multiplicative decomposition strategy (MDS) proposed by Kao and Hwang (2008) and the additive decomposition strategy (ADS) proposed by Chen et al. (2009). For the MDS, it interprets the system efficiency as the product of two sub-stage efficiencies, i.e., \(\theta_{o} = \theta_{o}^{1} \times \theta_{o}^{2}\). However, this approach suffer from several shortcomings, for example, it fails to handle the situations in which a VRS assumption is required, and it becomes nonlinear when additional constraints are included. To resolve these problems, Chen et al. (2009) aggregate the components of a two-stage process by interpreting the system efficiency as the weighted average of component efficiencies. In doing so, as we will introduce below, the corresponding model can be easily transformed into a linear one.

  3. In doing so, we can always guarantee a bounded solution to model (12). Otherwise, model (12) may be unbounded as the objective of this model is to maximize the value of \(\sum\nolimits_{i = 1}^{m} {\varpi_{i} x_{{i\sigma \left( {\ell + 1} \right)}} } + \sum\nolimits_{d = 1}^{D} {\zeta_{d} z_{{d\sigma \left( {\ell + 1} \right)}} }\), which may be infinity as one only restricts that the overall efficiency of concerned DMUs should be maintained.

  4. We do not include Qinghai, Tibet, Hong Kong, Macao, and Taiwan due to data limits.

  5. Although not all inventions can be regarded as a patent, and the patents are actually differing greatly in quality (Chen, et al., 2018), the PA is indeed a reasonable and reliable indicator of unobserved innovation output.

  6. Specifically, to guarantee the feasibility of our concerned models, according to Proposition 1, we set \(\varepsilon = 10^{ - 8}\). In addition, following Lee et al. (2019), our study focuses primarily on the VRS condition.

References

  • Acs, Z. J., Anselin, L., & Varga, A. (2002). Patents and innovation counts as measures of regional production of new knowledge. Research Policy, 31, 1069–1085.

    Article  Google Scholar 

  • Al-Siyabi, M., Amin, G. R., Bose, S., & Al-Masroori, H. (2019). Peer-judgment risk minimization using DEA cross-evaluation with an application in fishery. Annals of Operations Research, 274(1–2), 39–55.

    Article  Google Scholar 

  • Amin, G. R., & Toloo, M. (2004). A polynomial-time algorithm for finding epsilon in DEA models. Computers & Operations Research, 31(5), 803–805.

    Article  Google Scholar 

  • An, Q., Meng, F., Xiong, B., Wang, Z., & Chen, X. (2020). Assessing the relative efficiency of Chinese high-tech industries: A dynamic network data envelopment analysis approach. Annals of Operations Research, 290, 707–729.

    Article  Google Scholar 

  • Banker, R. D., Charnes, A., & Cooper, W. W. (1984). Some models for estimating technical and scale inefficiencies in data envelopment analysis. Management Science, 30, 1078–1092.

    Article  Google Scholar 

  • Carayannis, E. G., Grigoroudis, E., & Goletsis, Y. (2016). A multilevel and multistage efficiency evaluation of innovation systems: A multiobjective DEA approach. Expert Systems with Applications, 62, 63–80.

    Article  Google Scholar 

  • Charnes, A., & Cooper, W. W. (1962). Programming with linear fractional functionals. Naval Research Logistics (NRL), 9, 181–186.

    Article  Google Scholar 

  • Charnes, A., Cooper, W. W., & Rhodes, E. (1978). Measuring the efficiency of decision making units. European Journal of Operational Research, 2, 429–444.

    Article  Google Scholar 

  • Chen, C.-M., & van Dalen, J. (2010). Measuring dynamic efficiency: Theories and an integrated methodology. European Journal of Operational Research, 203, 749–760.

    Article  Google Scholar 

  • Chen, H. (2018). Average lexicographic efficiency for data envelopment analysis. Omega, 74, 82–91.

    Article  Google Scholar 

  • Chen, K., & Guan, J. (2012). Measuring the efficiency of China’s regional innovation systems: Application of Network Data Envelopment Analysis (DEA). Regional Studies, 46, 355–377.

    Article  Google Scholar 

  • Chen, K., & Kou, M. (2014). Staged efficiency and its determinants of regional innovation systems: A two-step analytical procedure. The Annals of Regional Science, 52(2), 627–657.

    Article  Google Scholar 

  • Chen, X., Liu, Z., & Zhu, Q. (2018). Performance evaluation of China’s high-tech innovation process: Analysis based on the innovation value chain. Technovation, 74, 42–53.

    Article  Google Scholar 

  • Chen, Y., Cook, W. D., Li, N., & Zhu, J. (2009). Additive efficiency decomposition in two-stage DEA. European Journal of Operational Research, 196, 1170–1176.

    Article  Google Scholar 

  • Chu, J., Wu, J., Chu, C., & Zhang, T. (2020). DEA-based fixed cost allocation in two-stage systems: Leader-follower and satisfaction degree bargaining game approaches. Omega, 94, 102054.

    Article  Google Scholar 

  • Cook, W. D., & Seiford, L. M. (2009). Data envelopment analysis (DEA)–Thirty years on. European Journal of Operational Research, 192, 1–17.

    Article  Google Scholar 

  • Despotis, D. K., Koronakos, G., & Sotiros, D. (2016a). Composition versus decomposition in two-stage network DEA: A reverse approach. Journal of Productivity Analysis, 45, 71–87.

    Article  Google Scholar 

  • Despotis, D. K., Koronakos, G., & Sotiros, D. (2016b). The “weak-link” approach to network DEA for two-stage processes. European Journal of Operational Research, 254(2), 481–492.

    Article  Google Scholar 

  • Emrouznejad, A., & Yang, G.-L. (2018). A survey and analysis of the first 40 years of scholarly literature in DEA: 1978–2016. Socio-Economic Planning Sciences, 61, 4–8.

    Article  Google Scholar 

  • Färe, R., & Grosskopf, S. (2000). Network DEA Network DEA. Socio-Economic Planning Sciences, 34, 35–49.

    Article  Google Scholar 

  • Galagedera, D. U., Roshdi, I., Fukuyama, H., & Zhu, J. (2018). A new network DEA model for mutual fund performance appraisal: An application to US equity mutual funds. Omega, 77, 168–179.

    Article  Google Scholar 

  • Gerami, J., Mavi, R. K., Saen, R. F., & Mavi, N. K. (2020). A novel network DEA-R model for evaluating hospital services supply chain performance. Annals of Operations Research. https://doi.org/10.1007/s10479-020-03755-w.

  • Golany, B., & Roll, Y. (1989). An application procedure for DEA. Omega, 17, 237–250.

    Article  Google Scholar 

  • Guan, J., & Chen, K. (2010a). Measuring the innovation production process: A cross-region empirical study of China’s high-tech innovations. Technovation, 30, 348–358.

    Article  Google Scholar 

  • Guan, J., & Chen, K. (2010b). Modeling macro-R&D production frontier performance: An application to Chinese province-level R&D. Scientometrics, 82, 165–173.

    Article  Google Scholar 

  • Guan, J., & Chen, K. (2012). Modeling the relative efficiency of national innovation systems. Research Policy, 41, 102–115.

    Article  Google Scholar 

  • Guo, C., Shureshjani, R. A., Foroughi, A. A., & Zhu, J. (2017). Decomposition weights and system efficiency in two-stage additive network DEA. European Journal of Operational Research, 257, 896–906.

    Article  Google Scholar 

  • Kao, C. (2014). Network data envelopment analysis: A review. European Journal of Operational Research, 239, 1–16.

    Article  Google Scholar 

  • Kao, C. (2017). Efficiency measurement and frontier projection identification for general two-stage systems in data envelopment analysis. European Journal of Operational Research, 261, 679–689.

    Article  Google Scholar 

  • Kao, C., & Hwang, S.-N. (2008). Efficiency decomposition in two-stage data envelopment analysis: An application to non-life insurance companies in Taiwan. European Journal of Operational Research, 185, 418–429.

    Article  Google Scholar 

  • Kao, C., & Liu, S.-T. (2019). Cross efficiency measurement and decomposition in two basic network systems. Omega, 83, 70–79.

    Article  Google Scholar 

  • Kogan, L., Papanikolaou, D., Seru, A., & Stoffman, N. (2017). Technological innovation, resource allocation, and growth. The Quarterly Journal of Economics, 132, 665–712.

    Article  Google Scholar 

  • Lee, J., Kim, C., & Choi, G. (2019). Exploring data envelopment analysis for measuring collaborated innovation efficiency of small and medium-sized enterprises in Korea. European Journal of Operational Research, 278(2), 533–545.

    Article  Google Scholar 

  • Liang, L., Cook, W. D., & Zhu, J. (2008). DEA models for two-stage processes: Game approach and efficiency decomposition. Naval Research Logistics (NRL), 55, 643–653.

    Article  Google Scholar 

  • Liu, J. S., & Lu, W.-M. (2010). DEA and ranking with the network-based approach: A case of R&D performance. Omega, 38, 453–464.

    Article  Google Scholar 

  • Liu, J. S., Lu, W. M., & Ho, M. H. C. (2015). National characteristics: Innovation systems from the process efficiency perspective. R&D Management, 45(4), 317–338.

    Article  Google Scholar 

  • Lu, W.-M., Kweh, Q. L., Nourani, M., & Huang, F.-W. (2016). Evaluating the efficiency of dual-use technology development programs from the R&D and socio-economic perspectives. Omega, 62, 82–92.

    Article  Google Scholar 

  • Mehrabian, S., Jahanshahloo, G. R., Alirezaee, M., & Amin, G. R. (2000). An assurance interval for the non-Archimedean epsilon in DEA models. Operations Research, 48(2), 344–347.

    Article  Google Scholar 

  • Oxman, J. A. (1992). The global service quality measurement program at American Express Bank. National Productivity Review, 11, 381–392.

    Article  Google Scholar 

  • Post, T., Cherchye, L., & Kuosmanen, T. (2002). Nonparametric efficiency estimation in stochastic environments. Operations Research, 50, 645–655.

    Article  Google Scholar 

  • Wang, K., Huang, W., Wu, J., & Liu, Y.-N. (2014). Efficiency measures of the Chinese commercial banking system using an additive two-stage DEA. Omega, 44, 5–20.

    Article  Google Scholar 

  • Wang, Q., Hang, Y., Sun, L., & Zhao, Z. (2016). Two-stage innovation efficiency of new energy enterprises in China: A non-radial DEA approach. Technological Forecasting and Social Change, 112, 254–261.

    Article  Google Scholar 

  • Xiong, X., Yang, G., & Guan, Z. (2018). Assessing R&D efficiency using a two-stage dynamic DEA model: A case study of research institutes in the Chinese Academy of Sciences. Journal of Informetrics, 12(3), 784–805.

    Article  Google Scholar 

  • Xu, S., Fang, L., & Govindan, K. (2022). Energy performance contracting in a supply chain with financially asymmetric manufacturers under carbon tax regulation for climate change mitigation. Omega, 106, 102535.

  • Zhang, B., Luo, Y., & Chiu, Y.-H. (2019). Efficiency evaluation of China’s high-tech industry with a multi-activity network data envelopment analysis approach. Socio-Economic Planning Sciences, 66, 2–9.

    Article  Google Scholar 

  • Zhu, Q., Wu, J., & Song, M. (2018). Efficiency evaluation based on data envelopment analysis in the big data context. Computers & Operations Research, 98, 291–300.

    Article  Google Scholar 

  • Zuo, K., & Guan, J. (2017). Measuring the R&D efficiency of regions by a parallel DEA game model. Scientometrics, 112, 175–194.

    Article  Google Scholar 

Download references

Acknowledgements

The authors would especially like to thank the editors, and three anonymous reviewers whose comments led to significant improvements in the paper. This work is supported by the National Natural Science Foundation of China under grant (No. 71671095), the Tianjin Philosophy and Social Science Planning Key Project (TJGL21-009), and the Fundamental Research Funds for the Central Universities (No. 2232021E-10).

Author information

Authors and Affiliations

  1. Glorious Sun School of Business and Management, Donghua University, No. 1882 West Yan’an Road, Shanghai, 200051, China

    Jiawei Yang

  2. Department of Management Science and Engineering, Business school, Nankai University, Nankai District, No. 121 Baidi Road, Tianjin, 300071, China

    Lei Fang

Authors
  1. Jiawei Yang
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Lei Fang
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Lei Fang.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

See Tables 13, 14, 15, 16, 17.

Table 13 The system efficiency of 29 provincial-level regions using the traditional ADA
Full size table
Table 14 The R&D efficiency of 29 provincial-level regions using the traditional ADA (under strategy I)
Full size table
Table 15 The commercialization efficiency of 29 provincial-level regions using the traditional ADA (under strategy I)
Full size table
Table 16 The R&D efficiency of 29 provincial-level regions using the traditional ADA (under strategy II)
Full size table
Table 17 The commercialization efficiency of 29 provincial-level regions using the traditional ADA (under strategy II)
Full size table

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yang, J., Fang, L. Average lexicographic efficiency decomposition in two-stage data envelopment analysis: an application to China’s regional high-tech innovation systems. Ann Oper Res 312, 1051–1093 (2022). https://doi.org/10.1007/s10479-021-04427-z

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10479-021-04427-z

Keywords