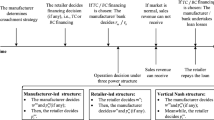
Abstract
This study analyzed how retailer overconfidence affects supply chain transparency for manufacturers who can encroach on the retail channel by paying a fixed entry cost. Both the reselling model and agent selling model were examined. The results show that an overconfident retailer has more incentive to increase the supply chain transparency in the reselling model than in the agency selling model. In detail, retailer overconfidence may lead to supply chain transparency even at a moderate channel substitution rate, and this effect can be enhanced with an increasing level of retailer overconfidence. This finding differs from conventional wisdom, which indicates that a retailer should not share any information if the channel substitution rate is not sufficiently high. The findings of this study are helpful to explain why some retailers voluntarily share information with manufacturers that have less-competitive direct selling channels. Additionally, from the perspective of entry cost, the results also indicate that an overconfident retailer can have more incentive than a normal retailer to increase the supply chain transparency in the reselling model. For the agent selling model, the results show that the above findings are reversed. Finally, whether using a wholesale or agency model, the retailer may benefit from its overconfidence bias in certain situations when it can voluntarily share information.







Similar content being viewed by others
References
Abhishek, V., Jerath, K., & Zhang, Z. J. (2015). Agency selling or reselling? Channel structures in electronic retailing. Management Science, 62(8), 2259–2280.
Amrouche, N., & Yan, R. (2016). A manufacturer distribution issue: How to manage an online and a traditional retailer. Annals of Operations Research, 244(2), 257–294.
Bolton, G. E., & Katok, E. (2008). Learning by doing in the newsvendor problem: A laboratory investigation of the role of experience and feedback. Manufacturing and Service Operations Management, 10(3), 519–538.
Bostian, A. A., Holt, C. A., & Smith, A. M. (2008). Newsvendor pull-to-center effect: Adaptive learning in a laboratory experiment. Manufacturing and Service Operations Management, 10(4), 590–608.
Camerer, C., & Lovallo, D. (1999). Overconfidence and excess entry: An experimental approach. American Economic Review, 89(1), 306–318.
Fawcett, S. E., Wallin, C., Allred, C., Fawcett, A. M., & Magnan, G. M. (2011). Information technology as an enabler of supply chain collaboration: A dynamic-capabilities perspective. Journal of Supply Chain Management, 47(1), 38–59.
Grubb, M. D. (2009). Selling to overconfident consumers. American Economic Review, 99(5), 1770–1807.
Guan, X., Liu, B., Chen, Y. J., & Wang, H. (2019). Inducing supply chain transparency through supplier encroachment. Production and Operations Management.
Guan, X., & Chen, Y. J. (2015). Hierarchical quality disclosure in a supply chain with cost heterogeneity. Decision Support Systems, 76, 63–75.
Guan, X., & Chen, Y. J. (2017). The interplay between information acquisition and quality disclosure. Production and Operations Management, 26(3), 389–408.
Guo, L. (2009). The benefits of downstream information acquisition. Marketing Science, 28(3), 457–471.
Guo, L. (2009). Quality disclosure formats in a distribution channel. Management Science, 55(9), 1513–1526.
Han, S., Fu, Y., Cao, B., & Luo, Z. (2018). Pricing and bargaining strategy of e-retail under hybrid operational patterns. Annals of Operations Research, 270(1–2), 179–200.
Ho, T. H., Lim, N., & Cui, T. H. (2010). Reference dependence in multilocation newsvendor models: A structural analysis. Management Science, 56(11), 1891–1910.
Huang, S., Guan, X., & Chen, Y. J. (2018). Retailer information sharing with supplier encroachment. Production and Operations Management, 27(6), 1133–1147.
Hu, W., & Li, Y. (2012). Retail service for mixed retail and E-tail channels. Annals of Operations Research, 192(1), 151–171.
Jiang, B., & Liu, C. (2019). Managerial optimism in a competitive market. Production and Operations Management, 28(4), 833–846.
Kirshner, S. N., & Shao, L. (2019). The overconfident and optimistic price-setting newsvendor. European Journal of Operational Research, 277(1), 166–173.
Li, M. (2019). Overconfident distribution channels. Production and Operations Management.
Li, G., Liu, M., Bian, Y., & Sethi, S. P. (2020). Guarding against disruption risk by contracting under information asymmetry. Decision Sciences.
Li, G., Zheng, H., Sethi, S. P., & Guan, X. (2018). Inducing downstream information sharing via manufacturer information acquisition and retailer subsidy. Decision Sciences.
Li, L. (2002). Information sharing in a supply chain with horizontal competition. Management Science, 48(9), 1196–1212.
Li, G., Li, L., & Sun, J. (2019). Pricing and service effort strategy in a dual-channel supply chain with showrooming effect. Transportation Research Part E: Logistics and Transportation Review, 126, 32–48.
Li, M., Petruzzi, N. C., & Zhang, J. (2016). Overconfident competing newsvendors. Management Science, 63(8), 2637–2646.
Li, T., Tong, S., & Zhang, H. (2014). Transparency of information acquisition in a supply chain. Manufacturing and Service Operations Management, 16(3), 412–424.
Li, G., Wu, H., & Xiao, S. (2020). Financing strategies for a capital-constrained manufacturer in a dual-channel supply chain. International Transactions in Operational Research, 27(5), 2317–2339.
Li, L., & Zhang, H. (2008). Confidentiality and information sharing in supply chain coordination. Management Science, 54(8), 1467–1481.
Pi, Z., Fang, W., & Zhang, B. (2019). Dual-channel operations: Implication of free-riding and decision bias. SSRN 3442777.
Plous, S. (1993). The psychology of judgment and decision making. New York: Mcgraw-Hill.
Ren, Y., & Croson, R. (2013). Overconfidence in newsvendor orders: An experimental study. Management Science, 59(11), 2502–2517.
Ren, Y., Croson, D. C., & Croson, R. T. A. (2017). The overconfident newsvendor. Journal of the Operational Research Society, 68(5), 496–506.
Russo, J. E., & Schoemaker, P. J. H. (1992). Managing overconfidence. Sloan Management Review.
Schweitzer, M. E., & Cachon, G. P. (2000). Decision bias in the newsvendor problem with a known demand distribution: Experimental evidence. Management Science, 46(3), 404–420.
Shen, Y., Willems, S. P., & Dai, Y. (2019). Channel selection and contracting in the presence of a retail platform. Production and Operations Management, 28(5), 1173–1185.
Sun, X., Tang, W., Chen, J., Li, S., & Zhang, J. (2019). Manufacturer encroachment with production cost reduction under asymmetric information. Transportation Research Part E: Logistics and Transportation Review, 128, 191–211.
Tan, Y., & Carrillo, J. E. (2017). Strategic analysis of the agency model for digital goods. Production and Operations Management, 26(4), 724–741.
Van den Steen, E. (2004). Rational overoptimism (and other biases). American Economic Review, 94(4), 1141–1151.
Wei, L., Zhang, J., & Zhu, G. (2020). Incentive of retailer information sharing on manufacturer volume flexibility choice. Omega, 102210.
Weinstein, N. D. (1980). Unrealistic optimism about future life events. Journal of Personality and Social Psychology, 39(5), 806.
Wirl, F. (2018). Agency model and wholesale pricing: Apple versus Amazon in the E-book market. International Journal of the Economics of Business, 25(2), 243–264.
Zhang, J., Li, S., Zhang, S., & Dai, R. (2019). Manufacturer encroachment with quality decision under asymmetric demand information. European Journal of Operational Research, 273(1), 217–236.
Zhang, S., & Zhang, J. (2020). Agency selling or reselling: E-Tailer information sharing with supplier offline entry. European Journal of Operational Research, 280(1), 134–151.
Zhu, C., & Yao, Z. (2018). Comparison between the agency and wholesale model under the e-book duopoly market. Electronic Commerce Research, 18(2), 313–337.
Acknowledgements
The work is financially supported by National Natural Science Funds of China (Nos. 72171219, 71971203, 71801206, 71921001), the Four Batch Talent Programs of China, the Fundamental Research Funds for the Central Universities (WK2040000027), USTC Research Funds of the Double First-Class Initiative (YD2040002004), and the Special Research Assistant Support Program of Chinese Academy of Sciences.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
1.1 Derivation of the equilibrium results of the reselling agreement
We note that the retailer observes the true demand after her information-sharing decision; thus, her overconfidence bias only affects that sharing decision. In other words, the retailer and manufacturer’s quantity decision and encroachment decision are independent of the retailer’s cognitive bias because when they make these decisions, the retailer already knows the exact demand and she is no longer overconfident. Thus, the proof structure closely follows that of Huang et al. (2018) and Zhang and Zhang (2020).
Case NN We first derive the equilibrium results when the retailer does not share information and the manufacturer does not encroach. This case is a traditional retail supply chain with asymmetric information. The retailer’s profit function is given by \(\pi _r(q_1)=(a +\theta - q_1 - w) q_1\), and it is straightforward to derive the retailer’s optimal quantity \(q_1(w)= \frac{a+\theta -w}{2} \). Observing only the prior distribution for the demand, the manufacturer sets the wholesale price to maximize his expected profit. We can solve the manufacturer’s problem for this Stackelberg game as \(\pi _m(w)=E_\theta \{w q_1(w)\}\), thus the manufacturer’s optimal wholesale price \(w^{NN}=\frac{a+d}{2}\). Substituting \(w^{NN}\) into the retailer’s best response \(q_1(w)\) and both firms’ profit functions, we obtain \(q_1^{NN}=\frac{a-d+2 \theta }{4}\), \(\pi _r^{NN}=\frac{(a-d+2 \theta )^2}{16}\) and \(\pi _m^{NN}=\frac{(a+d)^2}{8}\).
Case NE Since the manufacturer encroaches, there is quantity competition between the retail channel and direct channel. This case is a traditional dual channel supply chain with asymmetric information in which the downstream privately observes the demand information. The retailer’s and manufacturer’s profit functions can be expressed as \(\pi _r(q_1)=(a-b q_2+\theta -q_1-w) q_1\) and \(\pi _m(q_2,w)=E_\theta \{w q_1+(a-b q_1+\theta -q_2) q_2\}-I\), respectively. It is obvious that the retailer’s best response \(q_1(\ddot{q_2};w)=\frac{a-b \ddot{q_2}+\theta -w}{2}\). Similarly, the manufacturer’s best response is \(q_2(\ddot{q_1};w)=\frac{a+d-b E_\theta (\ddot{q_1})}{4-b^2}\). Here, we use “\(\ddot{}\)” to represent the conjectured variable. When the conjecture is consistent with the actual optimal decision, the Nash equilibrium is established, so we have \(q_1=\ddot{q_1}\) and \(q_2=\ddot{q_2}\). Solving these two equations jointly, the optimal quantity depends on the given wholesale price w, which can be expressed as \(q_1(w)=\frac{2 a (2-b)+b^2 (d-\theta )-2 b d-4 (w-\theta )}{2 \left( 4-b^2\right) }\) and \(q_2(w)=\frac{a (2-b)+(2-b) d+b w}{4-b^2}\). Because the manufacturer only observes the prior distribution for the demand, he uses only that to determine the wholesale price to maximize his expected profit. Thus the manufacturer’s optimal wholesale price \(w^{NE}=\frac{\left( b^3-4 b^2+8\right) (a+d)}{16-6 b^2}\). Substituting \(w^{NE}\) into the retailer’s best response \(q_1(w)\), the manufacturer’s best response \(q_2(w)\), and both firms’ profit functions, we obtain \(q_1^{NE}=\frac{4 a (1-b)-(2-b) (2+3 b)d+(8-3 b^2) \theta }{16-6 b^2}\), \(q_2^{NE}=\frac{(2-b) (4+b) (a+\theta )}{16-6 b^2}\), \(\pi _r^{NE}=\frac{(4 a (1-b)-(4+4 b-3 b^2) d+(8-3 b^2) \theta )^2}{4 (8-3 b^2)^2}\), and \(\pi _m^{NE}=\frac{(6-b) (2-b) (a+d)^2}{4 (8-3 b^2)}-I\).
Case SN In this case, the retailer shares information and the manufacturer does not encroach. This case is a traditional retail supply chain with symmetric information. The retailer’s profit function is given by \(\pi _r(q_1)=(a +\theta - q_1 - w) q_1\), and it is straightforward to derive the retailer’s optimal quantity \(q_1(w)= \frac{a+\theta -w}{2} \). The manufacturer also observes the true demand, so he determines the wholesale price using the true profit function. We can solve the manufacturer’s problem for this Stackelberg game as \(\pi _m(w)=w q_1(w)\), thus the manufacturer’s optimal wholesale price is \(w^{SN}=\frac{a+\theta }{2}\). Substituting \(w^{SN}\) into the retailer’s best response \(q_1(w)\) and both firms’ profit functions, we can obtain \(q_1^{SN}=\frac{a+\theta }{4}\), \(\pi _r^{SN}=\frac{1}{16} (a+\theta )^2\), and \(\pi _m^{SN}=\frac{1}{8} (a+\theta )^2\).
Case SE Here, the retailer shares information and the manufacturer encroaches. This case is a traditional dual channel supply chain with symmetric information, in which the upstream also observes the demand information. The retailer’s and manufacturer’s profit functions can be expressed as \(\pi _r(q_1)=(a-b q_2+\theta -q_1-w) q_1\) and \(\pi _m(q_2,w)=w q_1+(a-b q_1+\theta -q_2) q_2-I\), respectively. Similar to Case NE, using the first-order optimality condition and jointly finding solutions, we obtain the optimal quantity depends on the given wholesale price w, which can be expressed as \(q_1(w)=\frac{(2-b) (a+\theta )-2 w}{4-b^2}\) and \(q_2(w)=\frac{(2-b) (a+\theta )+b w}{4-b^2}\). The manufacturer can observe the true demand, so he determines the wholesale price to maximize his real profit function. Thus the manufacturer’s optimal wholesale price is \(w^{SE}=\frac{\left( b^3-4 b^2+8\right) (a+\theta )}{16-6 b^2}\). Substituting \(w^{SE}\) into the retailer’s best response \(q_1(w)\), the manufacturer’s best response \(q_2(w)\), and both firms’ profit functions, we can obtain \(q_1^{SE}=\frac{2 (1-b) (a+\theta )}{8-3 b^2}\), \(q_2^{SE}=\frac{(2-b) (4+b) (a+\theta )}{16-6 b^2}\), \(\pi _r^{SE}=\frac{4 (1-b)^2 (a+\theta )^2}{(8-3 b^2)^2}\), and \(\pi _m^{SE}=\frac{(6-b) (2-b) (a+\theta )^2}{4 (8-3 b^2)}-I\).
1.2 Derivation of the equilibrium results for the agency selling agreement
Case NN Similar to the previous proofs, we derive the equilibrium results under agency selling when the retailer does not share information and the manufacturer does not encroach. In this case, the manufacturer directly decides the retail price. The retailer’s and manufacturer’s profit functions can be expressed as \(\pi _r=r (a+\theta -q_1) q_1\) and \(\pi _m=E_\theta \{(1-r)(a+\theta -q_1) q_1\}\). Solving the first-order condition \(\frac{\partial \pi _r}{\partial q_1}=0\), the optimal order quantities to maximize the manufacturer’s expected profit can be given by \(q_1^{NN}=\frac{a+d}{2}\). Then, by substituting \(q_1^{NN}\) into both firms’ profit functions, we can obtain \(\pi _r^{NN} =\frac{r(a+d)(a-d+2 \theta )}{4}\) and \(\pi _m^{NN} =\frac{(1-r)(a+d)^2}{4}\).
Case NE Since the manufacturer encroaches, then there is quantity competition between the agency selling channel and the direct channel. This case, the downstream privately observes the demand information and does not share it. The retailer’s and manufacturer’s profit functions can be expressed as \(\pi _r=r(a+\theta -q_1-b q_2) q_1\) and \(\pi _m=E_\theta \{(1-r) (a+\theta -q_1-b q_2) q_1+(a+\theta -q_2-b q_1) q_2\}-I\), respectively. Similar to reselling agreement case, we solve the first-order condition \(\frac{\partial \pi _r}{\partial q_1}=0\) and \(\frac{\partial \{E_\theta \pi _m\}}{\partial q_2}=0\), simultaneously. The optimal order quantities to maximize the manufacturer’s expected profit are given by \(q_1^{NE}=\frac{(a+d) (2(1-r)-b (2-r))}{4 (1-r)-b^2 (2-r)^2}\) and \(q_2^{NE}=\frac{(a+d) (2-b (2-r)) (1-r)}{4 (1-r)-b^2 (2-r)^2}\). We note that \(q_1^{NE}\) must be positive, so we have \(b<\frac{2(1-r)}{2-r}\). Substituting \(q_1^{NE}\) and \(q_2^{NE}\) into both firms’ profit functions, we can obtain \(\pi _r^{NE}=\frac{((a+d) r (2 (1-r)-b (2-r)) (a (1-b) (2 (1-r)+b (2-r))-d (2 (1-r)-b r-b^2 (2-3 r+r^2))+(4 (1-r)-b^2 (2-r)^2) \theta ))}{(4 (1-r)-b^2 (2-r)^2)^2}\) and \(\pi _m^{NE}=\frac{(1-b) (a+d)^2 (2-3 r+r^2)}{4 (1-r)-b^2 (2-r)^2}-I\).
Case SN The retailer shares information and the manufacturer does not encroach. This case is an agency selling supply chain with symmetric information. The retailer’s and manufacturer’s profit functions can be expressed as \(\pi _r=r(a+\theta -q_1) q_1\) and \(\pi _m=(1-r) (a+\theta -q_1) q_1\), respectively. Solving the first-order condition, the optimal order quantity to maximize the manufacturer’s true profit is \(q_1^{SN}=\frac{a+\theta }{2}\). Then, by substituting \(q_1^{SN}\) into both firms’ profit functions, we can obtain \(\pi _r^{SN}=\frac{r (a+\theta )^2}{4}\) and \(\pi _m^{SN}=\frac{(1-r) (a+\theta )^2}{4}\).
Case SE The retailer shares information and the manufacturer encroaches. This case is an agency selling dual channel supply chain with symmetric information, in which the upstream also observes the demand information. The retailer’s and manufacturer’s profit functions can be expressed as \(\pi _r=r (a+\theta -q_1-b q_2) q_1\) and \(\pi _m=(1-r) (a+\theta -q_1-b q_2) q_1+(a+\theta -q_2-b q_1) q_2-I\), respectively. The optimal order quantities to maximize the manufacturer’s true profit are \(q_1^{SE}=\frac{(a+\theta ) (2 (1-r)-b (2-r)) }{4 (1-r)-b^2 (2-r)^2}\) and \(q_2^{SE}=\frac{(a+\theta ) (2-b (2-r)) (1-r) }{4 (1-r)-b^2 (2-r)^2}\). Substituting \(q_1^{SE}\) and \(q_2^{SE}\) into both firms’ profit functions, we can obtain \(\pi _r^{SE}=\frac{r (1-b) (4 (1-r)^2-b^2 (2-r)^2) (a+\theta )^2}{(4 (1-r)-b^2 (2-r)^2)^2}\) and \(\pi _m^{SE}=\frac{(1-b) (2-r) (1-r) (a+\theta )^2}{4 (1-r)-b^2 (2-r)^2}-I\).
Proof of Lemma 1
If the retailer does not share the demand information with the manufacturer, the manufacturer decides whether to encroach by comparing the expected profit for cases NE and NN. That means that the manufacturer encroaches when \(\frac{(12-8 b+b^2) (a+d)^2}{4 (8-3 b^2)}-I-\frac{1}{8} (a+d)^2 \ge 0\), which reduces to \(I \le \frac{(16-16 b+5 b^2) (a+d)^2}{8 (8-3 b^2)}\). When the retailer shares demand information with the manufacturer, the manufacturer decides whether to encroach by comparing the profit for Cases SE and SN. Then, the manufacturer encroaches if and only if \(\frac{(6-b) (2-b) (a+\theta )^2}{4 (8-3 b^2)}-I-\frac{1}{8} (a+\theta )^2\ge 0\), which is \(I\le \frac{(16-16 b+5 b^2) (a+\theta )^2}{8 (8-3 b^2)}\), due to \(0\le \theta \le 2d\) Therefore, \(\frac{(16-16 b+5 b^2)a^2}{8 (8-3 b^2)} \le \frac{(16-16 b+5 b^2) (a+\theta )^2}{8 (8-3 b^2)}\le \frac{(16-16 b+5 b^2) (a+2d)^2}{8 (8-3 b^2)}\). Then, we conclude that if \(I\le \frac{(16-16 b+5 b^2)a^2}{8 (8-3 b^2)}\), then the manufacturer always encroaches no matter what market potential is, while if the entry cost \(I>\frac{(16-16 b+5 b^2) (a+2d)^2}{8 (8-3 b^2)}\), the manufacturer never encroaches. In addition, when the entry cost is moderate, the manufacturer encroaches when \(I\le \frac{(16-16 b+5 b^2) (a+\theta )^2}{8 (8-3 b^2)}\), which equivalent to \(\theta \ge \sqrt{\frac{8 (8-3 b^2)I}{16-16 b+5 b^2}}-a\). Moreover, because the retailer is overconfident, she makes a decision as though the demand potential were \(\Theta :=\alpha d+(1-\alpha )\theta \), rather than the given true demand potential \(\theta \). We define \(I_0=\frac{(16-16 b+5 b^2) (a+d)^2}{8 (8-3 b^2)}\), \(I_1=\frac{(16-16 b+5 b^2) (a+\alpha d )^2}{8 (8-3 b^2)}\), and \(I_2=\frac{(16-16 b+5 b^2) (a+2d-\alpha d )^2}{8 (8-3 b^2)}\), and we note that \(I_1<I_0<I_2\). Therefore, we can get the overconfident retailer’s expected profit before demand disclosed as the following:
where \(\hat{\Theta }=\alpha d+(1-\alpha )(\sqrt{\frac{8 (8-3 b^2)I}{16-16 b+5 b^2}}-a)\). \(\square \)
Proof of Proposition 1
We examine the monotonicity of \(\pi _r^{N}(I)\) and \(\pi _r^{S}(I)\) with entry cost I where \(I_1<I\le I_2\). We know \(\frac{\partial \pi _r^{S}}{\partial \hat{\Theta }}=\frac{b (4+b) (8-3 b) (4-3 b) (a+\hat{\Theta })^2}{32 (8-3 b^2)^2 d (1-\alpha )}>0\) for \(0<b<1\) and \(\hat{\Theta }\) is increasing in I. Thus, \(\pi _r^{S}(I)\) is increasing in I. Also, letting \(\pi _r^{N}|_{I\le I_0}-\pi _r^{N}|_{I>I_0}=-(\frac{b (4+b) (8-3 b) (4-3 b)}{16(8-3 b^2)^2}) (a+d)^2<0\), we know \(\pi _r^{N}(I)\) is also increasing in I. The retailer’s expected profit has a sudden upward jump at \(I_0\) in the no-sharing condition. Based on the monotonicity of \(\pi _r^{N}(I)\) and \(\pi _r^{S}(I)\), it is essential to compare \(\pi _r^{N}(I_0)\) and \(\pi _r^{S}(I_0)\) to determine the retailer’s information decision when \(I_1<I\le I_0\). Next, we define \(g(b, \alpha )=\pi _r^{S}(I_0)-\pi _r^{N}(I_0)\) and derive \(\frac{\partial g(b, \alpha )}{\partial b}=\frac{4 (1-b) (8-6 b+3 b^2) (3 a^2+3 a d (1+\alpha )-d^2 (1-5 \alpha +\alpha ^2))}{3 (8-3 b^2)^3}>0\) for \(0<b<1\), \(a>2d\), and \(0<\alpha <1\), which represent that \(g(b, \alpha )\) is increasing in b. Simultaneously, we can derive \(g(0, \alpha )=-\frac{d^2 (1-\alpha )^2}{16}<0\) and \(g(1, \alpha )=\frac{3 a^2+3 a d (1+\alpha )-d^2 (7-17 \alpha +7 \alpha ^2)}{96}>0\) for \(0<b<1\), \(a>2d\), and \(0<\alpha <1\). Hence there exists a unique solution \(b^{*}\) satisfying \(g(b^{*}, \alpha )=0\), such that \(g(b, \alpha )<0\) if \(b<b^*\), and \(g(b, \alpha )>0\) otherwise. If \(b>b^*\), there exists a unique threshold \(I^*\) satisfying \(\pi _r^{N}(I^*)=\pi _r^{S}(I^*)\), such that \(\pi _r^{N}(I^*)<\pi _r^{S}(I^*)\) for \(I^*<I<I_0\). Furthermore, \(\frac{\partial g(b, \alpha )}{\partial \alpha }=\frac{3 a b (128-112 b+9 b^3) d+d^2 (768+640 b-1136 b^2+153 b^4-(768+256 b-800 b^2+126 b^4) \alpha )}{96 (8-3 b^2)^2}\), so \(\frac{\partial ^2 g(b, \alpha )}{\partial \alpha ^2}=-\frac{(384+128 b-400 b^2+63 b^4) d^2}{48 (8-3 b^2)^2}<0\) for \(0<b<1\) and \(d>0\). This implies that \(\frac{\partial g(b, \alpha )}{\partial \alpha }\) is decreasing in \(\alpha \), thus \(\frac{\partial g(b, \alpha )}{\partial \alpha }>\frac{\partial g(b, \alpha )}{\partial \alpha }|_{\alpha =1}=\frac{b (128-112 b+9 b^3) d (a+d)}{32 (8-3 b^2)^2}>0\). Therefore, \(g(b, \alpha )\) is strictly increasing in \(\alpha \). Combined with our knowledge that \(g(b, \alpha )\) is increasing in b, we see that \(b^*\) is the unique solution to \(g(b, \alpha )=0\), hence \(b^*\) is decreasing in \(\alpha \). \(\square \)
Proof of Proposition 2
We define \(G(\hat{\Theta }^*,b,d,\alpha )=\frac{(a+\hat{\Theta }^* )^3-(a+\alpha d)^3}{48(2d-2\alpha d)}+\frac{4 (1-b)^2 ((a+2d-\alpha d)^3-(a+\hat{\Theta }^* )^3)}{3(8-3 b^2)^2(2d-2\alpha d)}-\frac{4 (1-b)^2(a+d)^2}{(8-3 b^2)^2}- \frac{d^2(1-\alpha )^2}{12}\), where \(\hat{\Theta }^*=\alpha d+(1-\alpha )(\sqrt{\frac{8 (8-3 b^2)I^*}{16-16 b+5 b^2}}-a)\). It is obvious that \(\frac{dI^*}{d\hat{\Theta }^*}>0\). Based on the Implicit Function Theorem, we have \(\frac{\partial I^*}{\partial \alpha }=\frac{\partial I^*}{\partial \hat{\Theta }^*}\times \frac{\partial \hat{\Theta }^*}{\partial \alpha }=\frac{\partial I^*}{\partial \hat{\Theta }^*}\cdot (-\frac{\partial G}{\partial \alpha }/\frac{\partial G}{\partial \hat{\Theta }^*})\). Similarly, \(\frac{\partial I^*}{\partial b}=\frac{\partial I^*}{\partial \hat{\Theta }^*}\times \frac{\partial \hat{\Theta }^*}{\partial b}=\frac{\partial I^*}{\partial \hat{\Theta }^*}\cdot (-\frac{\partial G}{\partial b}/\frac{\partial G}{\partial \hat{\Theta }^*})\). We consider the first-order derivatives of \(G(\hat{\Theta }^*,b,d,\alpha )\) with respect to \(\hat{\Theta }^*\) and b as follows:
Both of these are increasing in \(\hat{\Theta }^*\), and \(\alpha d<\hat{\Theta }^*<d\), so we have \(\frac{\partial G}{\partial b}\ge \frac{4 (1-b) (8-6 b+3 b^2) (3 a^2+3 a d (1+\alpha )-d^2 (1-5 \alpha +\alpha ^2))}{3 (8-3 b^2)^3}>0\) for \(0<b<1\) and \(a>2d>0\), thus \(\frac{\partial I^*}{\partial b}<0\). The first-order derivative of \(G(\hat{\Theta }^*,b,d,\alpha )\) with \(\alpha \) is
Letting \(G'(\alpha )=\frac{\partial G}{\partial \alpha }\), we can derive \(G''(\alpha )=-\frac{1}{48 (8-3 b^2)^2 d (1-\alpha )^3}(d^3 (384 (1-\alpha )^3+128 b (2-3 \alpha +3 \alpha ^2-\alpha ^3)+9 b^4 (8-21 \alpha +21 \alpha ^2-7 \alpha ^3)-16 b^2 (32-75 \alpha +75 \alpha ^2-25 \alpha ^3))+3 a^2 b (128-112 b+9 b^3) (d-\hat{\Theta }^* )-b (128-112 b+9 b^3) \hat{\Theta }^{*3}+3 a b (128-112 b+9 b^3) (d^2-\hat{\Theta }^{*2}))\), and \(G'''(\alpha )=-\frac{b (4+b) (8-3 b) (4-3 b)(d-\hat{\Theta }^* ) (3 a^2+d^2+d \hat{\Theta }^* +\hat{\Theta }^{*2}+3 a (d+\hat{\Theta }^* ))}{16 (8-3 b^2)^2 d (1-\alpha )^4}>0\) for \(0<b<1\) and \(\hat{\Theta }^*<d\). Then, \(G''(\alpha )\le G''(0)=-\frac{(384+128 b-400 b^2+63 b^4) d^2}{48 (8-3 b^2)^2}<0\) for \(\hat{\Theta }^*=d\). Therefore, \(G'(\alpha )\) is strictly decreasing in \(\alpha \), and \(G'(\alpha )<G'(0)<0\) for \(a>2d\) and \(0<b<1\). Therefore, \(\frac{\partial I^*}{\partial \alpha }<0\); that is, \(I^*\) is decreasing in \(\alpha \). \(\square \)
Proof of Lemma 2
If the agency selling retailer does not share the information with the manufacturer, the manufacturer decides whether to encroach by comparing the expected profit for cases NE and NN, as was done for the reselling case. The manufacturer encroaches when \(\frac{(1-b)\ (2-r) (1-r)(a+d)^2}{4 (1-r)-b^2 (2-r)^2}-I-\frac{(a+d)^2 (1-r)}{4}\ge 0\), which reduces to \(I \le \tilde{I_0} =\frac{(1-r)(2-b (2-r))^2 (a+d)^2 }{4 (4 (1-r)-b^2 (2-r)^2)}\). If the agency selling retailer shares demand information with the manufacturer, the manufacturer decides whether to encroach by comparing the profit for Cases SE and SN. The manufacturer encroaches if and only if \(\frac{(1-b) (2-r) (1-r) (a+\theta )^2}{4 (1-r)-b^2 (2-r)^2}-I-\frac{(1-r) (a+\theta )^2}{4} \ge 0\), which is equivalent to \(I\le \frac{(1-r) (2-b (2-r))^2 (a+\theta )^2}{4 (4 (1-r)-b^2 (2-r)^2)}\), due to \(0\le \theta \le 2d\). Thus, we have \(\frac{(1-r) (2-b (2-r))^2 a^2}{4 (4 (1-r)-b^2 (2-r)^2)} \le \frac{(1-r) (2-b (2-r))^2 (a+\theta )^2}{4 (4 (1-r)-b^2 (2-r)^2)} \le \frac{(1-r) (2-b (2-r))^2 (a+2d )^2}{4 (4 (1-r)-b^2 (2-r)^2)}\). Then we can get that if \(I\le \frac{(1-r) (2-b (2-r))^2 a^2}{4 (4 (1-r)-b^2 (2-r)^2)}\), the manufacturer always encroaches no matter what market potential is, while if the entry cost \(I>\frac{(1-r) (2-b (2-r))^2 (a+2d )^2}{4 (4 (1-r)-b^2 (2-r)^2)}\), the manufacturer never encroaches. When the entry cost is moderate, the manufacturer encroaches when \(I\le \frac{(1-r) (2-b (2-r))^2 (a+\theta )^2}{4 (4 (1-r)-b^2 (2-r)^2)}\), which is equivalent to \(\theta \ge \sqrt{\frac{4 (4 (1-r)-b^2 (2-r)^2)I}{(1-r) (2-b (2-r))^2 }}-a\). Moreover, when the retailer is overconfident, she makes her decision as though the demand potential were \(\Theta :=\alpha d+(1-\alpha )\theta \), rather than the given true demand potential \(\theta \). We define \(\tilde{I_1} =\frac{(1-r) (2-b (2-r))^2 a^2}{4 (4 (1-r)-b^2 (2-r)^2)}\) and \(\tilde{I_2}=\frac{(1-r) (2-b (2-r))^2 (a+2d )^2}{4 (4 (1-r)-b^2 (2-r)^2)}\). Therefore, we can get the overconfident retailer’s expected profit before demand disclosed as the following:
where \(\tilde{\Theta }= \alpha d+(1-\alpha )(\sqrt{\frac{4 (4 (1-r)-b^2 (2-r)^2)I}{(1-r) (2-b (2-r))^2 }}-a)\). \(\square \)
Proof of Proposition 3
Similar to the proof of Proposition 1, we examine the monotonicity of \(\tilde{\pi }_r^{N}(I)\) and \(\tilde{\pi }_r^{S}(I)\) with entry cost I where \(\tilde{I_1}<I\le \tilde{I_2}\). We know \(\frac{\partial \pi _r^{S}}{\partial \hat{\Theta }}=\frac{b r (16 (1-r)^2-4 b^2 (2-r)^2+b^3 (2-r)^4-4 b (2-r)^2 (1-2 r)) (a+\theta )^2}{8 d (b^2 (2-r)^2-4 (1-r))^2 (1-\alpha )}>0\) for \(0<b<\frac{2(1-r)}{2-r}\), and \(\tilde{\Theta }\) is increasing in I obviously, thus \(\tilde{\pi }_r^{S}(I)\) is increasing in I. Also, \(\tilde{\pi }_r^{N}|_{I\le I_0}-\tilde{\pi }_r^{N}|_{I>I_0}<0\), so \(\tilde{\pi }_r^{N}(I)\) is also increasing in I. The retailer’s expected profit has a sudden upward jump at \(\tilde{I_0}\) in the no-sharing condition. Based on the monotonicity of \(\tilde{\pi }_r^{N}(I)\) and \(\tilde{\pi }_r^{S}(I)\), it is essential to compare \(\tilde{\pi }_r^{N}(\tilde{I_0})\) and \(\tilde{\pi }_r^{S}(\tilde{I_0})\) to determine the retailer’s information decision. Next, we define \(f(b, \alpha )=\tilde{\pi }_r^{S}(\tilde{I_0})-\tilde{\pi }_r^{N}(\tilde{I_0})\) and derive that \(f(0, \alpha )=-\frac{r(3 a^2 \alpha +3 a d (4-3 \alpha ) \alpha +d^2 (-2+18 \alpha -24 \alpha ^2+9 \alpha ^3))}{24 (1-\alpha )}>0\) for \(0<b<\frac{2(1-r)}{2-r}\) and \(\alpha <\tilde{\alpha }^*\). In this, \(\tilde{\alpha }^*\) is the unique solution of \(\frac{a(a+4d)^2}{4d^3}-2+18 \alpha -24 \alpha ^2+9 \alpha ^3=0\) for \(0<\alpha <1\) and \(f(\frac{2(1-r)}{2-r}, \alpha )=-\frac{r (3 a^2-3 a d (-3+\alpha )-d^2 (-5+\alpha +\alpha ^2))}{24}<0\). Simultaneously, \(\frac{\partial g(b, \alpha )}{\partial b}<0\), which represents that \(f(b, \alpha )\), is decreasing in b. Hence there exists a unique solution \(\tilde{b}^{*}\) satisfying \(f(\tilde{b}^{*}, \alpha )=0\), such that \(f(b, \alpha )>0\) if \(b<\tilde{b}^*\) and \(f(b, \alpha )<0\) otherwise for \(\alpha <\tilde{\alpha }^*\). Since \(b<\tilde{b}^*\), there exists a unique threshold \(\tilde{I}^*\) satisfying \(\tilde{\pi }_r^{N}(I^*)=\tilde{\pi }_r^{S}(I^*)\), such that \(\tilde{\pi }_r^{N}(\tilde{I}^*)<\tilde{\pi }_r^{S}(\tilde{I}^*)\) for \(\tilde{I}_0<I<\tilde{I}^*\). Denoting \(h(\alpha )=\frac{\partial f(b, \alpha )}{\partial \alpha }\), we can derive \(h''(\alpha )=\frac{(1-b) (3 a^2+3 a d+d^2) (b^2 (2-r)^2-4 (1-r)^2) r}{(b^2 (2-r)^2-4 (1-r))^2 (1-\alpha )^4}<0\). This means that \(h'(\alpha )\) decreasing in \(\alpha \) and \(h'(\alpha )<h'(0)<0\). Therefore, \(f(b, \alpha )\) is decreasing in \(\alpha \) for \(0<\alpha <\tilde{\alpha }^*\). Moreover, \(f(b,\alpha )\) is decreasing in b, and \(\tilde{b}^*\) is the unique solution to \(f(b,\alpha )=0\), thus, \(\tilde{b}^*\) is decreasing in \(\alpha \). \(\square \)
Proof of Proposition 4
The proof of the monotonicity of \(\tilde{I}^*\) with \(\alpha \) can be analogously analyzed when the reselling agreement is used. We define \(F(\tilde{\Theta }^*,b,d,\alpha )=\frac{r((a+\tilde{\Theta }^*)^3 -(a+\alpha d)^3)}{12(2d-2 \alpha d)}+\frac{r(1-b) (4 (1-r)^2-b^2 (2-r)^2) ((a+2d-2 \alpha d)^3-(a+\tilde{\Theta }^*)^3)}{3(b^2 (2-r)^2-4 (1-r))^2(2d-2 \alpha d)}-\frac{r(a+d)^2}{4}\), where \(\tilde{\Theta }^*= \alpha d+(1-\alpha )(\sqrt{\frac{4 (4 (1-r)-b^2 (2-r)^2)\tilde{I}^*}{(1-r) (2-b (2-r))^2 }}-a)\). By the Implicit Function Theorem, we have \(\frac{\partial \tilde{I}^*}{\partial \alpha }=\frac{\partial \tilde{I}^*}{\partial }\times \frac{\partial \tilde{\Theta }^*}{\partial \alpha }=\frac{\partial \tilde{I}^*}{\partial \tilde{\Theta }^*}\cdot (-\frac{\partial F}{\partial \alpha }/\frac{\partial F}{\partial \tilde{\Theta }^*})\). It is obvious that \(\frac{d\tilde{I}^*}{d\tilde{\Theta }^*}>0\), \(\frac{\partial F}{\partial \tilde{\Theta }^*}>0\) and \(\frac{\partial F}{\partial \alpha }<0\) which can be examined in a similar way for \(0<\alpha <\tilde{\alpha }^*\) and \(0<b<\tilde{b}^*\). This gives us \(\frac{\partial \tilde{I}^*}{\partial \alpha }>0\) in this circumstance. \(\square \)
Rights and permissions
About this article
Cite this article
Lu, W., Jiang, Y., Xia, P. et al. How retailer overconfidence affects supply chain transparency with manufacturer encroachment. Ann Oper Res 329, 1149–1174 (2023). https://doi.org/10.1007/s10479-021-04494-2
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10479-021-04494-2