Optimal pricing and greening decisions in a supply chain when considering market segmentation

Abstract

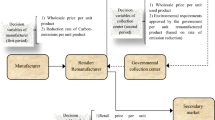
This study investigates the optimal pricing and the remanufactured product’s greening decisions in a supply chain consisting of one manufacturer and one retailer. Under manufacturer-led Stackelberg games, three remanufacturing systems, namely, centralized, decentralized manufacturer, and decentralized retailer-remanufacturing, are considered. Consumers in the market are divided into normal and green consumers according to whether they consider environmental issues. We first demonstrate the conditions under which the manufacturer or retailer should engage in remanufacturing. Second, despite cannibalization, a centralized remanufacturing system exhibits higher efficiency linked with higher market coverage and leads to a higher profit compared to manufacturer/retailer decentralized alternatives. Finally, numerical studies and sensitivity analyses are used to examine the sensitivity of optimal pricing and greening decisions.

Appendix

1.1 Proof of Proposition 1

When $0\le p_R\le \delta p_N$, then:

$$\begin{aligned} \pi _{L}^C= & {} \left\{ (1-\gamma )\left( 1-\frac{p_N-p_R}{1-\delta }\right) +\gamma \left( 1-\frac{p_N-p_R+ke}{1-\delta }\right) \right\} (p_N-c_N)\\&+\left\{ (1-\gamma )\left( \frac{p_N-p_R}{1-\delta }-\frac{p_R}{\delta }\right) +\,\gamma \left( \frac{p_N-p_R+ke}{1-\delta }-\frac{p_R-ke}{\delta }\right) \right\} (p_R-c_R)-\beta e^2. \end{aligned}$$

The first order condition are $\frac{\partial \pi _{L}^C}{\partial e}= \frac{-2(1-\delta )\beta \delta e-\gamma k[\delta (p_N-c_N)-(p_R-c_R)]}{(1-\delta )\delta }$and $\frac{\partial \pi _{L}^C}{\partial p_R}= \frac{-2p_R+\delta (2p_N-c_N) +c_R+\gamma k e}{(1-\delta )\delta }$. the second order derivatives can be written as:

$$\begin{aligned} \frac{\partial ^2 \pi _{L}^C}{\partial e^2}= & {} -2\beta<0,\\ \frac{\partial ^2 \pi _{L}^C}{\partial p_R^2}= & {} \frac{-2}{(1-\delta )\delta }<0,\\ \frac{\partial ^2 \pi _{L}^C}{\partial e\partial p_R}= & {} \frac{\gamma k}{(1-\delta )\delta }. \end{aligned}$$

The determinant of the Hessian can be written as: $|H|=\frac{4(1-\delta )\beta \delta -\gamma ^2 k^2}{(1-\delta )^2\delta ^2}>0$. Thus, we have get the green rate e the price of remanufactured product which can maximize the manufacturer’s and the retailer’s profit by solving $\frac{\partial \pi _{L}^C}{\partial e}=0$ and $\frac{\partial \pi _{L}^C}{\partial p_R}=0$, that are, $e=\frac{\gamma k(\delta c_N-\delta p_N+p_R-c_R)}{2(1-\delta )\beta \delta }$ and $p_R=\delta p_N+\frac{c_R-c_N\delta +\gamma k e}{2}$.

Assuming $\delta c_N>c_R$, $\frac{2(1-\delta )\beta \delta }{k^2}<\gamma \le \min \left\{ \frac{\sqrt{2(1-\delta )\beta \delta }}{k},\frac{4(1-\delta )\beta \delta }{k^2}\right\}$ and substituting e into $p_R$, we have $p_R=\delta p_N-\frac{(\delta c_N-c_R)[2(1-\delta )\beta \delta )-\gamma ^2 k^2]}{4(1-\delta )\beta \delta -\gamma ^2 k^2}$. .

Solving the two equations together, we have

$$\begin{aligned} e=\frac{(\delta c_N-c_R)\gamma k}{4(1-\delta )\beta \delta -\gamma ^2k^2} \end{aligned}$$

and

$$\begin{aligned} p_R=\delta p_N-\frac{(\delta c_N-c_R)[2(1-\delta )\beta \delta )-\gamma ^2 k^2]}{4(1-\delta )\beta \delta -\gamma ^2 k^2}. \end{aligned}$$

Substituting e and $p_R$ in to $\pi _{M}$, then differentiating $\pi _{L}^C$ with respect to $p_N$, we have

$$\begin{aligned} \frac{\partial \pi _{L}^C}{\partial p_N}=1-2p_N+c_N \end{aligned}$$

and

$$\begin{aligned} \frac{\partial ^2 \pi _{L}^C}{\partial p^2_N}=-2 \end{aligned}$$

As $\frac{\partial ^2 \pi _{L}^C}{\partial p_N^2}<0$, we have $p_N$ which can maximize the profit by solving $\frac{\partial \pi _{L}^C}{\partial p_N}=0$, that is,

$$\begin{aligned} p_{NL}^{C*}=\frac{1+c_N}{2}. \end{aligned}$$

Then when $0\le p_R< \delta p_N$ and $\frac{ 2(1-\delta )\beta \delta }{k^2}\le \gamma \le \frac{\sqrt{2(1-\delta )\beta \delta }}{k}$, substituting $p_{NL}^{C*}$ in to e and $p_R$, we have

$$\begin{aligned} e_{L}^{C*}= & {} \frac{(\delta c_N-c_R)\gamma k}{4(1-\delta )\beta \delta -\gamma ^2k^2},\\ p_{RL}^{C*}= & {} \frac{(1+c_N)\delta }{2}-\frac{[2(1-\delta )\beta \delta -\gamma ^2 k^2](\delta c_N-c_R)}{4(1-\delta )\beta \delta -\gamma ^2k^2} \end{aligned}$$

and

$$\begin{aligned} \pi _{L}^{C*}= \frac{(1-c_N)^2}{4}+\frac{(\delta c_N-c_R)^2\beta }{4(1-\delta )\beta \delta -\gamma ^2 k^2}. \end{aligned}$$

1.2 Proof of Proposition 2

Assume $\delta p_N< p_R\le \delta p_N+ke$, then:

$$\begin{aligned} \pi _{M}^C= & {} \left\{ (1-\gamma )(1-p_N)+\gamma \left( 1-\frac{p_N-p_R+ke}{1-\delta }\right) \right\} (p_N-c_N)\\&+\left\{ \gamma \left( \frac{p_N-p_R+ke}{1-\delta }-\frac{p_R-ke}{\delta }\right) \right\} (p_R-c_R)-\beta e^2. \end{aligned}$$

With the same method in the case $0\le p_R\le \delta p_N$, the determinant of the Hessian can be written as: $|H|=\frac{\gamma [4(1-\delta )\beta \delta -\gamma k^2]}{(1-\delta )^2\delta ^2}>0$. Thus, we have get the greenness level e and the price of the remanufactured product by solving $\frac{\partial \pi _{M}^C}{\partial e}=0$ and $\frac{\partial \pi _{M}^C}{\partial p_{R}}=0$, that are, $e=\frac{\gamma k(\delta c_N-\delta p_N+p_R-c_R)}{2(1-\delta )\beta \delta }$ and $p_R=\delta p_N+\frac{c_R-c_N\delta + k e}{2}$.

As $\delta c_N>c_R$, solving the two equations together, we have

$$\begin{aligned} e=\frac{(\delta c_N-c_R)\gamma k}{4(1-\delta )\beta \delta -\gamma k^2} \end{aligned}$$

and

$$\begin{aligned} p_R=\delta p_N+\frac{[\gamma k^2-2(1-\delta )\beta \delta ](\delta c_N-c_R)}{4(1-\delta )\beta \delta -\gamma k^2}. \end{aligned}$$

Substituting e and $p_R$ in to $\pi _{M}^C$, then differentiating $\pi _{M}^C$ with respect to $p_N$, we have

$$\begin{aligned} \frac{\partial \pi _{M}^C}{\partial p_N}=1-2p_N+c_N \end{aligned}$$

and

$$\begin{aligned} \frac{\partial ^2 \pi _{M}^C}{\partial p^2_N}=-2 \end{aligned}$$

As $\frac{\partial ^2 \pi _{M}^C}{\partial p_N^2}<0$, we have $p_N$ which can maximize the profit by solving $\frac{\partial \pi _{M}^C}{\partial p_N}=0$, that is,

$$\begin{aligned} p_{NM}^{C*}=\frac{1+c_N}{2}. \end{aligned}$$

Then substituting $p_{NM}^C$ in to e and $p_R$, we have

$$\begin{aligned} e_{M}^{C*}= & {} \frac{(\delta c_N-c_R)\gamma k}{4(1-\delta )\beta \delta -\gamma k^2},\\ p_{RM}^{C*}&==&\frac{(1+c_N)\delta }{2}+\frac{[\gamma k^2-2(1-\delta )\beta \delta ](\delta c_N-c_R)}{4(1-\delta )\beta \delta -\gamma k^2} \end{aligned}$$

and

$$\begin{aligned} \pi _{M}^{C*}=\frac{(1-c_N)^2}{4}+\frac{\beta \gamma (\delta c_N-c_R)^2}{4(1-\delta )\beta \delta -\gamma k^2} \end{aligned}$$

1.3 Proof of Proposition 3

Assume $\delta p_N+ke<p_R\le p_N$, $\pi _{H}^C=(1-p_N)(p_N-c_N)$, we can get $p_N$ which can maximize the profit by solving $\frac{\partial \pi _{H}^C}{\partial p_N}=0$, that is,

$$\begin{aligned} p_{NH}^{C*}=\frac{1+c_N}{2} \end{aligned}$$

and

$$\begin{aligned} \pi _{H}^{C*}=\frac{(1-c_N)^2}{4} \end{aligned}$$

1.4 Proof of Proposition 4

By comparing the profits in the three price strategies, then we have

• (I) It is obvious that $\pi _{H}^{C*}<\pi _{H}^{L*}$ and $\pi _{H}^{C*}<\pi _{H}^{M*}$

• (II) Then we compare $\pi _{H}^{L*}$ and $\pi _{H}^{L*}$

$\pi _{L}^{C*}-\pi _{M}^{C*}=\frac{\beta (1-\gamma )(\delta c_N-c_R)^2[4\beta \delta (1-\delta )-\gamma k^2-\gamma ^2 k^2]}{[4\beta \delta (1-\delta )-\gamma k^2][4\beta \delta (1-\delta )-\gamma ^2 k^2]}$. As $\pi _{L}^{C*}-\pi _{M}^{C*}$ has same symbol with $4\beta \delta (1-\delta )-\gamma k^2-\gamma ^2 k^2$ and $4\beta \delta (1-\delta )-\gamma k^2-\gamma ^2 k^2$ is a concave function of $\gamma$. By solving it equals to 0, we have $\gamma =\frac{-\sqrt{16(1-\delta )\beta \delta +k^2}-k}{2k}$ or $\gamma =\frac{\sqrt{16(1-\delta )\beta \delta +k^2}-k}{2k}$. As $\gamma >0$ and denoting $\gamma _1=\frac{\sqrt{16(1-\delta )\beta \delta +k^2}-k}{2k}$, it is easy to get $\frac{2(1-\delta )\beta \delta }{k^2}<\gamma _1<\min \left\{ \frac{4(1-\delta )\beta \delta }{k^2}, ~\frac{\sqrt{2(1-\delta )\beta \delta }}{k}\right\}$. Thus we can conclude $\pi _{L}^{C*}\ge \pi _{M}^{C*}$ when $\frac{2(1-\delta )\beta \delta }{k^2}<\gamma \le \gamma _1$; $\pi _{L}^{C*}<\pi _{M}^{C*}$ when $\gamma _1<\gamma <\min \left\{ \frac{4(1-\delta )\beta \delta }{k^2}, ~\frac{\sqrt{2(1-\delta )\beta \delta }}{k}\right\}$.

1.5 Proof of Proposition 5

Assume that $0\le p_R\le \delta p_N$ and $\frac{2(1-\delta )\beta \delta }{k^2}<\gamma \le \min \left\{ \frac{\sqrt{2(1-\delta )\beta \delta }}{k},\frac{4(1-\delta )\beta \delta }{k^2}\right\}$, then:

$$\begin{aligned} \pi _{RL}^M= & {} \left\{ (1-\gamma )\left( 1-\frac{p_N-p_R}{1-\delta }\right) +\gamma \left( 1-\frac{p_N-p_R+ke}{1-\delta }\right) \right\} (p_N-w_N)\\&+\,\left\{ (1-\gamma )\left( \frac{p_N-p_R}{1-\delta }-\frac{p_R}{\delta }\right) +\gamma \left( \frac{p_N-p_R+ke}{1-\delta }-\frac{p_R-ke}{\delta }\right) \right\} (p_R-w_R). \end{aligned}$$

The first order condition are $\frac{\partial \pi _{RL}^M}{\partial p_N}= \frac{-2(p_N-p_R)+1+w_N-w_R-\delta -\gamma k e}{1-\delta }$and $\frac{\partial \pi _{RL}^M}{\partial p_R}= \frac{-2p_R+\delta (2p_N-w_N) +w_R+\gamma k e}{(1-\delta )\delta }$. the second order derivatives can be written as:

$$\begin{aligned} \frac{\partial ^2 \pi _{RL}^M}{\partial p_N^2}= & {} \frac{-2}{1-\delta }<0,\\ \frac{\partial ^2 \pi _{RL}^M}{\partial p_R^2}= & {} \frac{-2}{(1-\delta )\delta }<0,\\ \frac{\partial ^2 \pi _{RL}^M}{\partial p_N\partial p_R}= & {} \frac{2}{1-\delta }. \end{aligned}$$

The determinant of the Hessian can be written as: $|H|=\frac{4}{(1-\delta )\delta }>0$. Thus, we have get the price of new product and the remanufactured one which can maximize the manufacturer’s and the retailer’s profit by solving $\frac{\partial \pi _{RL}^M}{\partial p_N}=0$ and $\frac{\partial \pi _{RL}^M}{\partial p_R}=0$, that are, $p_N=p_R+\frac{1+w_N-w_R-\delta -\gamma ke}{2}$ and $p_R=\delta p_N+\frac{w_R-\delta w_N+\gamma k e}{2}$. Solving the two equations together, we have

$$\begin{aligned} p_R=\frac{\delta +w_R+\gamma ke}{2} \end{aligned}$$

and

$$\begin{aligned} p_N=\frac{1+w_N}{2}. \end{aligned}$$

Substituting $p_R$ and $p_N$ into $\pi _{ML}^M$, and then differentiating $\pi _{ML}^M$ with respect to $w_R$ and e, we have

$$\begin{aligned}&\frac{\partial \pi _{ML}^M}{\partial w_R}=\frac{-2(w_R-\delta w_N)+c_R-\delta c_N+\gamma k e}{2(1-\delta )\delta }\\&\frac{\partial ^2 \pi _{ML}^M}{\partial w_R^2}=\frac{-1}{(1-\delta )\delta }\\&\frac{\partial ^2 \pi _{ML}^M}{\partial w_R\partial e}=\frac{\gamma k}{2(1-\delta )\delta }\\&\frac{\partial \pi _{ML}^M}{\partial e}=\frac{-4(1-\delta )\beta \delta e+(\delta c_N-\delta w_N+w_R-c_R)\gamma k}{2(1-\delta )\delta }\\&\frac{\partial ^2 \pi _{ML}^M}{\partial e^2}=-2\beta \end{aligned}$$

The determinant of the Hessian can be written as: $|H|=\frac{8(1-\delta )\beta \delta -\gamma ^2 k^2}{4(1-\delta )^2\delta ^2}>0$. Thus, we can get the wholesale price and greenness rate of remanufactured product which can maximize the manufacturer’s and the retailer’s profit by solving $\frac{\partial \pi _{ML}^M}{\partial w_R}=0$ and $\frac{\partial \pi _{ML}^M}{\partial e}=0$, that are,

$$\begin{aligned} w_R=\delta w_N-\frac{(\delta c_N-c_R)[4(1-\delta )\beta \delta -\gamma ^2 k^2]}{8(1-\delta )\beta \delta -\gamma ^2 k^2} \end{aligned}$$

and

$$\begin{aligned} e=\frac{(\delta c_N-c_R)\gamma k}{8(1-\delta )\beta \delta -\gamma ^2 k^2}. \end{aligned}$$

Substituting $w_R$ and e into $\pi _{ML}^M$, and then differentiating $\pi _{ML}^M$ with respect to $w_N$, we have

$$\begin{aligned} \frac{\partial \pi _{ML}^M}{\partial w_N}=-w_N+\frac{1+c_N}{2} \end{aligned}$$

and

$$\begin{aligned} \frac{\partial ^2 \pi _{ML}^M}{\partial w_N^2}=-1. \end{aligned}$$

As $\frac{\partial ^2 \pi _{ML}^M}{\partial w_N^2}<0$, by solving $\frac{\partial \pi _{ML}^M}{\partial w_N}=0$, we get $w_{NL}^{M*}=\frac{1+c_N}{2}$ which can maximize the manufacturer’s profit.

Substituting $w_{NL}^{M*}$ into $w_R$, e, $p_N$,$p_R$, $\pi _R$ and $\pi _M$, then

$$\begin{aligned} w_{RL}^{M*}= & {} \frac{\delta (1+c_N) }{2}-\frac{(\delta c_N-c_R)[4(1-\delta )\beta \delta -\gamma ^2 k^2]}{8(1-\delta )\beta \delta -\gamma ^2 k^2}\\ e_L^{M*}= & {} \frac{(\delta c_N-c_R)\gamma k}{8(1-\delta )\beta \delta -\gamma ^2 k^2} \\ p_{NL}^{M*}= & {} \frac{3+c_N}{4} \\ p_{RL}^{M*}&==&\frac{\delta (3+c_N)}{4}-\frac{[2(1-\delta )\beta \delta -\gamma ^2 k^2](\delta c_N-c_R)}{8(1-\delta )\beta \delta -\gamma ^2k^2} \\ \pi _{RL}^{M*}= & {} \frac{(1-c_N)^2}{16}+\frac{4(\delta c_N-c_R)^2(1-\delta )\beta ^2\delta }{[8(1-\delta )\beta \delta -\gamma ^2 k^2]^2}\\ \pi _{ML}^{M*}= & {} \frac{(1-c_N)^2}{8}+\frac{(\delta c_N-c_R)^2\beta }{8(1-\delta )\beta \delta -\gamma ^2 k^2} \end{aligned}$$

1.6 Proof of Proposition 6

Assume $\delta p_N< p_R\le \delta p_N+ke$. Then:

$$\begin{aligned} \pi _{RM}^M= & {} \left\{ (1-\gamma )(1-p_N)+\gamma \left( 1-\frac{p_N-p_R+ke}{1-\delta }\right) \right\} (p_N-w_N)\\&+\,\left\{ \gamma \left( \frac{p_N-p_R+ke}{1-\delta }-\frac{p_R-ke}{\delta }\right) \right\} (p_R-w_R). \end{aligned}$$

With the same method in the case $0\le p_R\le \delta p_N$, the determinant of the Hessian can be written as: $|H|=\frac{4\gamma }{(1-\delta )\delta }>0$. With $\frac{2(1-\delta )\beta \delta }{k^2}<\gamma <\frac{4(1-\delta )\beta \delta }{k^2}\le 1$, we have get the price of new and remanufactured product are, $p_N=\frac{w_N}{2}+\frac{1-\delta -\gamma k e+\gamma (2p_R-w_R)}{2(1-\delta +\gamma \delta )}$ and $p_R=\delta p_N+\frac{w_R-\delta w_N+ke}{2}$.

Solving the two equations together, we have

$$\begin{aligned} p_N=\frac{1+w_N}{2} \end{aligned}$$

and

$$\begin{aligned} p_R=\frac{\delta + w_R+ke}{2}. \end{aligned}$$

Substituting $p_N$ and $p_R$ in to $\pi _{MM}^M$, then differentiating $\pi _{MM}^M$ with respect to e and $w_R$, we have

$$\begin{aligned} \frac{\partial \pi _{MM}^M}{\partial w_R}= & {} \frac{(-2 w_R+2\delta w_N-\delta c_N+c_R+ke)\gamma }{2(1-\delta )\delta }\\ \frac{\partial ^2 \pi _{MM}^M}{\partial w_R^2}= & {} \frac{-\gamma }{(1-\delta )\delta }\\ \frac{\partial ^2 \pi _{MM}^M}{\partial e \partial w_R}= & {} \frac{\gamma k}{2(1-\delta )\delta }\\ \frac{\partial \pi _{MM}^M}{\partial e}= & {} \frac{-4(1-\delta )\beta \delta e+(\delta c_N-\delta w_N+w_R-c_R)\gamma k}{2(1-\delta )\delta }\\ \frac{\partial ^2 \pi _{MM}^M}{\partial e^2}= & {} -2\beta \end{aligned}$$

The determinant of the Hessian can be written as: $|H|=\frac{\gamma [8(1-\delta )\beta \delta -\gamma k^2]}{4(1-\delta )^2\delta ^2}>0$. Thus, we can get the wholesale price and greenness rate of remanufactured product which can maximize the manufacturer’s and the retailer’s profit by solving $\frac{\partial \pi _{MM}^M}{\partial w_R}=0$ and $\frac{\partial \pi _{MM}^M}{\partial e}=0$, that are,

$$\begin{aligned} w_R=\delta w_N+\frac{c_R-\delta c_N+ke}{2} \end{aligned}$$

and

$$\begin{aligned} e=\frac{(\delta c_N-\delta w_N+w_R-c_R)\gamma k}{4(1-\delta )\beta \delta }. \end{aligned}$$

solving the two equations together, we have

$$\begin{aligned} w_R=\delta w_N-\frac{(\delta c_N-c_R)[4(1-\delta )\beta \delta -\gamma k^2]}{8(1-\delta )\beta \delta -\gamma k^2} \end{aligned}$$

Solving $\frac{\partial \pi _{MM}^M}{\partial w_R}=0$ and $\frac{\partial \pi _{MM}^M}{\partial e}=0$ together, we have

$$\begin{aligned} w_R=\delta w_N-\frac{(\delta c_N-c_R)[4(1-\delta )\beta \delta -\gamma k^2]}{8(1-\delta )\beta \delta -\gamma k^2} \end{aligned}$$

and

$$\begin{aligned} e=\frac{(\delta c_N-c_R)\gamma k}{8(1-\delta )\beta \delta -\gamma k^2}. \end{aligned}$$

Substituting $w_R$ and e into $\pi _{MM}^M$, and then differentiating it with respect to $w_N$, we have

$$\begin{aligned} \frac{\partial \pi _{MM}^M}{\partial w_N}=-w_N+\frac{1+c_N}{2} \end{aligned}$$

and

$$\begin{aligned} \frac{\partial ^2 \pi _{MM}^M}{\partial w_N^2}=-1. \end{aligned}$$

As $\frac{\partial ^2 \pi _{MM}^M}{\partial w_N^2}<0$, by solving $\frac{\partial \pi _{MM}^M}{\partial w_N}=0$, we get $w_{NM}^{M*}=\frac{1+c_N}{2}$ which can maximize the manufacturer’s profit.

Substituting $w_{NM}^{M*}$ into $w_R$, e, $p_N$,$p_R$, $\pi _R$ and $\pi _M$, then

$$\begin{aligned} w_{RM}^{M*}= & {} \frac{\delta (1+c_N)}{2}-\frac{(\delta c_N-c_R)[4(1-\delta )\beta \delta -\gamma k^2]}{8(1-\delta )\beta \delta -\gamma k^2}\\ e_M^{M*}= & {} \frac{(\delta c_N-c_R)\gamma k}{8(1-\delta )\beta \delta -\gamma k^2}\\ p_{NM}^{M*}= & {} \frac{3+c_N}{4}\\ p_{RM}^{M*}= & {} \frac{\delta (3+c_N)}{4}+\frac{[\gamma k^2-2(1-\delta )\beta \delta ](\delta c_N-c_R)}{8(1-\delta )\beta \delta -\gamma k^2}\\ \pi _{RM}^{M*}= & {} \frac{(1-c_N)^2}{16}+\frac{4(1-\delta )(\delta c_N-c_R)^2\beta ^2\gamma \delta }{[8(1-\delta )\beta \delta -\gamma k^2]^2}\\ \pi _{MM}^{M*}= & {} \frac{(1-c_N)^2}{8}+\frac{(\delta c_N-c_R)^2\gamma \beta }{8(1-\delta )\beta \delta -\gamma k^2} \end{aligned}$$

1.7 Proof of Proposition 7

Assume $\delta p_N+ke<p_R\le p_N$, $\pi _{RH}^M=(1-p_N)(p_N-w_N)$, we can get $p_N$ which can maximize the profit by solving $\frac{\partial \pi _{RH}^M}{\partial p_N}=0$, that is,

$$\begin{aligned} p_{N}=\frac{1+w_N}{2} \end{aligned}$$

and

$$\begin{aligned} \pi _{RH}^{M}=\frac{(1-w_N)^2}{4} \end{aligned}$$

Substituting $p_N$ into $\pi _M$, we have

$$\begin{aligned} \pi _{MH}^M=\frac{(1-w_N)(w_N-c_N)}{2} \end{aligned}$$

By differentiating $\pi _{MH}^M$ with respect to $w_N$, we have

$$\begin{aligned} \frac{\partial \pi _{MH}^M}{\partial w_N}=-w_N+\frac{1+c_N}{2} \end{aligned}$$

and

$$\begin{aligned} \frac{\partial ^2 \pi _{MH}^M}{\partial w_N^2}=-1 \end{aligned}$$

As $\frac{\partial ^2\pi _{MH}^M}{\partial w_N^2}<0$, by solving $\frac{\partial \pi _{MH}^M}{\partial w_N}=0$, we have

$$\begin{aligned} w_{NH}^{M*}=\frac{1+c_N}{2} \end{aligned}$$

Substituting $w_N$ into $p_N$,$\pi _{MH}^M$,$\pi _{RH}^M$, we have

$$\begin{aligned} w_{NH}^{M*}= & {} \frac{3+c_N}{4}\\ \pi _{MH}^{M*}= & {} \frac{(1-c_N)^2}{8} \end{aligned}$$

and

$$\begin{aligned} \pi _{RH}^{M*}=\frac{(1-c_N)^2}{16}. \end{aligned}$$

1.8 Proof of Proposition 8

• (I) Comparing the manufacturer’s profits in three price strategies, we can see the case of the high pricing strategy leads to the smallest profit. Thus we compare other two strategies.

  $$\begin{aligned} \pi _{ML}^{M*}-\pi _{MM}^{M*}=\frac{(\delta c_N-c_R)^2(1-\gamma )\beta [-\gamma ^2k^2-\gamma k^2+8(1-\delta )\beta \delta ] }{[8(1-\delta )\beta \delta -\gamma k^2][8(1-\delta )\beta \delta -\gamma k^2]} \end{aligned}$$

  The symbol of $\pi _{ML}^{M*}-\pi _{MM}^{M*}$ depends on $-\gamma ^2k^2-\gamma k^2+8(1-\delta )\beta \delta$. Since $-\gamma ^2k^2-\gamma k^2+8(1-\delta )\beta \delta$ is a concave and continue function of $\gamma$ and $\Delta =k^4+32(1-\delta )\beta \delta k^2>0$, by solving $-\gamma ^2k^2-\gamma k^2+8(1-\delta )\beta \delta =0$, we have two roots $\frac{-k-\sqrt{32(1-\delta )\beta \delta +k^2}}{2k}<0$ and $\frac{-k+\sqrt{32(1-\delta )\beta \delta +k^2}}{2k}$. Denoting ${{\bar{\gamma }}}=\frac{-k+\sqrt{32(1-\delta )\beta \delta +k^2}}{2k}$, with $0\le \delta \le 1$ and $k^2\ge 4(1-\delta )\beta \delta$, it is easy to get ${{\bar{\gamma }}}>\frac{2(1-\delta )\beta \delta }{k^2}$. By comparing ${{\bar{\gamma }}}$ with $\min \left\{ \frac{\sqrt{2(1-\delta )\beta \delta }}{k},\frac{4(1-\delta )\beta \delta }{k^2}\right\}$, we have (i) $\frac{\sqrt{2(1-\delta )\beta \delta }}{k}\le \frac{4(1-\delta )\beta \delta }{k^2}$ when $2\sqrt{(1-\delta )\beta \delta }<k\le 2\sqrt{2(1-\delta )\beta \delta }$, then we get ${{\bar{\gamma }}}> \frac{\sqrt{2(1-\delta )\beta \delta }}{k}$; (ii) $\frac{\sqrt{2(1-\delta )\beta \delta }}{k}\ge \frac{4(1-\delta )\beta \delta }{k^2}$ when $2\sqrt{2(1-\delta )\beta \delta }<k<1$, then we get ${{\bar{\gamma }}}>\frac{4(1-\delta )\beta \delta }{k^2}$. We can summarize $\pi _{ML}^{M*}>\pi _{MM}^{M*}$.

• (II) Comparing the retailer’s and the manufacturer’s total profits in three price strategies, we can see the case of the high pricing strategy leads to the smallest profit. Thus we compare other two strategies.

$$\begin{aligned} \pi _{RL}^{M*}+\pi _{ML}^{M*}-(\pi _{RM}^{M*}+\pi _{MM}^{M*})=\frac{(\delta c_N-c_R)^2(1-\gamma )\beta F}{[8(1-\delta )\beta \delta -\gamma k^2]^2[8(1-\delta )\beta \delta -\gamma k^2]^2} \end{aligned}$$

where $F=-\gamma ^5 k^6+k^4[12(1-\delta )\beta \delta -k^2]\gamma ^4+28(1-\delta )\beta \delta k^4\gamma ^3-12(1-\delta )\beta \delta k^2[16\beta \delta (1-\delta )-k^2]\gamma ^2-192(1-\delta )^2\beta ^2\delta ^2k^2\gamma +768(1-\delta )^3\beta ^3\delta ^3$.

Since $\frac{2\beta \delta (1-\delta )}{k^2}<\gamma < \min \left\{ \frac{4\beta \delta (1-\delta )}{k^2},~~\frac{\sqrt{2\beta \delta (1-\delta )}}{k}\right\} \le 1$, we have $\frac{(\delta c_N-c_R)^2(1-\gamma )\beta }{[8(1-\delta )\beta \delta -\gamma k^2]^2[8(1-\delta )\beta \delta -\gamma k^2]^2}>0$. Thus the symbol of $\pi _{RL}^{M*}+\pi _{ML}^{M*}-(\pi _{RM}^{M*}+\pi _{MM}^{M*})$ is depend on F. In order to determine the symbol of F, by differentiating F with respect to $\gamma$, we have

$$\begin{aligned} \frac{\partial F}{\partial \gamma }= & {} -5\gamma ^4 k^6+4k^4[12(1-\delta )\beta \delta -k^2]\gamma ^3+84(1-\delta )\beta \delta k^4\gamma ^2\\&-24(1-\delta )\beta \delta k^2[16\beta \delta (1-\delta )-k^2]\gamma -192(1-\delta )^2\beta ^2\delta ^2k^2\\ \frac{\partial ^2 F}{\partial \gamma ^2}= & {} 4\{-(5\gamma +3)k^4\gamma ^2+6(1-\delta )\beta \delta k^2(1+7\gamma +6\gamma ^2)-96(1-\delta )^2\beta ^2\delta ^2\}k^2\\ \frac{\partial ^3 F}{\partial \gamma ^3}= & {} 12\{14(1-\delta )\beta \delta +24(1-\delta )\beta \delta \gamma -(5\gamma +2)\gamma k^2\}k^4 \\ \frac{\partial ^4 F}{\partial \gamma ^4}= & {} 24\{12(1-\delta )\beta \delta -(5\gamma +1)k^2\}k^4 \\ \frac{\partial ^5 F}{\partial \gamma ^5}= & {} -120k^6 \end{aligned}$$

Since F is continuous when $\frac{2\beta \delta (1-\delta )}{k^2}< \gamma < \min \left\{ \frac{4\beta \delta (1-\delta )}{k^2},~~\frac{\sqrt{2\beta \delta (1-\delta )}}{k}\right\} \le 1$, $\frac{\partial ^5 F}{\partial \gamma ^5}<0$ and $k\ge 0$, we can get $\frac{\partial ^4 F}{\partial \gamma ^4}$ is decreasing in $\gamma$. In addition, when $\gamma \le \frac{12(1-\delta )\beta \delta -k^2}{5k^2}$, i.e., $\frac{\partial ^4 F}{\partial \gamma ^4}\ge 0$, $\frac{\partial ^3 F}{\partial \gamma ^3}$ is increasing in $\gamma$; when $\frac{12(1-\delta )\beta \delta -k^2}{5k^2}<\gamma$, $\frac{\partial ^3 F}{\partial \gamma ^3}$ is decreasing in $\gamma$. As $\frac{12(1-\delta )\beta \delta -k^2}{5k^2}<\frac{2\beta \delta (1-\delta )}{k^2}$, $\frac{\partial ^4 F}{\partial \gamma ^4}<0$ then $\frac{\partial ^3 F}{\partial \gamma ^3}$ is decreasing in $\gamma$.

Furthermore, $\frac{\partial ^3 F}{\partial \gamma ^3}|_{{\gamma =\frac{2\beta \delta (1-\delta )}{k^2}}^+}=24\beta \delta (1-\delta )k^2[14\beta \delta (1-\delta )+5k^2]>0$ and $\frac{\partial ^3 F}{\partial \gamma ^3}|_{{\gamma =\frac{4\beta \delta (1-\delta )}{k^2}}^-}=24\beta \delta (1-\delta )k^2[8\beta \delta (1-\delta )+3k^2]>0$. We can conclude that $\frac{\partial ^2 F}{\partial \gamma ^2}$ is increasing in $\gamma$. And we have $\frac{\partial ^2 F}{\partial \gamma ^2}|_{{\gamma =\frac{2\beta \delta (1-\delta )}{k^2}}^+}=8(1-\delta )\beta \delta \{52(1-\delta )^2\beta ^2\delta ^2-12(1-\delta )\beta \delta k^2+3k^4\}>0$, $\frac{\partial ^2 F}{\partial \gamma ^2}|_{{\gamma =\frac{4\beta \delta (1-\delta )}{k^2}}^-}=8(1-\delta )\beta \delta \{128\beta ^2\delta ^2(1-\delta )^2+12\beta \delta (1-\delta )k^2+3k^4\}>0$. Thus $\frac{\partial F}{\partial \gamma }$ is increasing in $\gamma$.

With $\frac{2\beta \delta (1-\delta )}{k^2}< \gamma < \min \left\{ \frac{4\beta \delta (1-\delta )}{k^2},~~\frac{\sqrt{2\beta \delta (1-\delta )}}{k}\right\} \le 1$, we have

$$\begin{aligned} \frac{\partial F}{\partial \gamma }|_{{\gamma =\frac{2\beta \delta (1-\delta )}{k^2}}^+}=\frac{16\beta ^2\delta ^2(1-\delta )^2\{-9k^4+\beta \delta (1-\delta )[56\beta \delta (1-\delta )-29k^2]\}}{k^2}<0, \end{aligned}$$

(A.1)

and

$$\begin{aligned} \frac{\partial F}{\partial \gamma }|_{{\gamma =\frac{4\beta \delta (1-\delta )}{k^2}}^-}=\frac{32\beta ^2\delta ^2(1-\delta )^2\{-3k^4+\beta \delta (1-\delta )[56\beta \delta (1-\delta )-14k^2]\}}{k^2}<0, \end{aligned}$$

(A.2)

we can conclude that F is decreasing in $\gamma \in \left( \frac{2\beta \delta (1-\delta )}{k^2},\min \left\{ \frac{4\beta \delta (1-\delta )}{k^2},~~\frac{\sqrt{2\beta \delta (1-\delta )}}{k}\right\} \right)$.

• (i) when $k\ge 2\sqrt{2\beta \delta (1-\delta )}$, we have $\frac{4\beta \delta (1-\delta )}{k^2}\le \frac{\sqrt{2\beta \delta (1-\delta )}}{k}$;

  Moreover, we have $F|_{{\gamma =\frac{2\beta \delta (1-\delta )}{k^2}}^+}=\frac{16(1-\delta )^3\beta ^2\delta ^3\{27k^4-35(1-\delta )\beta \delta k^2+10(1-\delta )^2\beta ^2\delta ^2\}}{k^4}>0$ and $F|_{{\gamma =\frac{4\beta \delta (1-\delta )}{k^2}}^-}=\frac{64\beta ^3\delta ^3(1-\delta )^3\{3k^4-24\beta \delta (1-\delta )k^2+32(1-\delta )^2\beta ^2\delta ^2\}}{k^4}$. Since $k^2>8\beta \delta (1-\delta )$, $F|_{{\gamma =\frac{4\beta \delta (1-\delta )}{k^2}}^-}>0$ which implying F is always positive. The symbol of $\pi _{RL}^{M*}+\pi _{ML}^{M*}-(\pi _{RM}^{M*}+\pi _{MM}^{M*})$ is the same as F, then the proposition is approved.

• (ii) when $4\beta \delta (1-\delta )\le k<2\sqrt{2\beta \delta (1-\delta )}$, we have $\frac{4\beta \delta (1-\delta )}{k^2}>\frac{\sqrt{2\beta \delta (1-\delta )}}{k}$;

Similarly, we have $F|_{{\gamma =\frac{2\beta \delta (1-\delta )}{k^2}}^+}>0$ and $F|_{{\gamma =\frac{\sqrt{2\beta \delta (1-\delta )}}{k}}^-}>0$ which implying F is always positive. The symbol of $\pi _{RL}^{M*}+\pi _{ML}^{M*}-(\pi _{RM}^{M*}+\pi _{MM}^{M*})$ is the same as F, then the proposition is approved.

1.9 Proof of Proposition 9

Assume that $0\le p_R\le \delta p_N$ and $\frac{ 2(1-\delta )\beta \delta }{k^2}<\gamma <\frac{ 4(1-\delta )\beta \delta }{k^2}\le 1$. Then:

$$\begin{aligned} \pi _{RL}^R= & {} \left\{ (1-\gamma )\left( 1-\frac{p_N-p_R}{1-\delta }\right) +\gamma \left( 1-\frac{p_N-p_R+ke}{1-\delta }\right) \right\} (p_N-w_N)\\&+\left\{ (1-\gamma )\left( \frac{p_N-p_R}{1-\delta }-\frac{p_R}{\delta }\right) +\gamma \left( \frac{p_N-p_R+ke}{1-\delta }-\frac{p_R-ke}{\delta }\right) \right\} (p_R-c_R)-\beta e^2. \end{aligned}$$

The first order condition are $\frac{\partial \pi _{RL}^R}{\partial e}= \frac{-2(1-\delta )\beta \delta e-\gamma k[\delta (p_N-w_N)-(p_R-c_R)]}{(1-\delta )\delta }$and $\frac{\partial \pi _{RL}^R}{\partial p_R}= \frac{-2p_R+\delta (2p_N-w_N) +c_R+\gamma k e}{(1-\delta )\delta }$. the second order derivatives can be written as:

$$\begin{aligned} \frac{\partial ^2 \pi _{RL}^R}{\partial e^2}= & {} -2\beta<0,\\ \frac{\partial ^2 \pi _{RL}^R}{\partial p_R^2}= & {} \frac{-2}{(1-\delta )\delta }<0,\\ \frac{\partial ^2 \pi _{RL}^R}{\partial e\partial p_R}= & {} \frac{\gamma k}{(1-\delta )\delta }. \end{aligned}$$

The determinant of the Hessian can be written as: $|H|=\frac{4(1-\delta )\beta \delta -\gamma ^2 k^2}{(1-\delta )^2\delta ^2}>0$. Thus, we have get the green rate e the price of remanufactured product which can maximize the manufacturer’s and the retailer’s profit by solving $\frac{\partial \pi _{RL}^R}{\partial e}=0$ and $\frac{\partial \pi _{RL}^R}{\partial p_R}=0$, that are, $e=\frac{\gamma k(\delta w_N-\delta p_N+p_R-c_R)}{2(1-\delta )\beta \delta }$ and $p_{R}=\delta p_N+\frac{c_R-w_N\delta +\gamma k e}{2}$.

As $\delta w_N>c_R$ and $\frac{2(1-\delta )\beta \delta }{k^2}<\gamma \le \min \left\{ \frac{\sqrt{2(1-\delta )\beta \delta }}{k},\frac{4(1-\delta )\beta \delta }{k^2}\right\}$ by solving two equations together, we have

$$\begin{aligned} e=\frac{(\delta w_N-c_R)\gamma k}{4(1-\delta )\beta \delta -\gamma ^2k^2} \end{aligned}$$

and

$$\begin{aligned} p_R=\delta p_N-\frac{[2(1-\delta )\beta \delta -\gamma ^2 k^2](\delta w_N-c_R)}{4(1-\delta )\beta \delta -\gamma ^2k^2}. \end{aligned}$$

By substituting e and $p_R$ in to $\pi _{RL}^R$, then differentiating $\pi _{RL}^R$ with respect to $p_N$, we have

$$\begin{aligned} \frac{\partial \pi _{RL}^R}{\partial p_N}=1-2p_N+w_N \end{aligned}$$

and

$$\begin{aligned} \frac{\partial ^2 \pi _{RL}^R}{\partial p^2_N}=-2 \end{aligned}$$

As $\frac{\partial ^2 \pi _{RL}^R}{\partial p_N^2}<0$, we have $p_N$ which can maximize the profit by solving $\frac{\partial \pi _{RL}^R}{\partial p_N}=0$, that is,

$$\begin{aligned} p_N=\frac{1+w_N}{2}. \end{aligned}$$

Substituting $p_N$, e and $p_R$ into $\pi _{ML}^R$, and differentiating $\pi _{ML}^R$, we have $\frac{\partial \pi _{ML}^R}{\partial w_N}= \frac{1}{2}-\frac{(4\beta \delta -\gamma ^2 k^2)(2w_N-c_N)+4\beta \delta c_R}{2[4(1-\delta )\beta \delta -\gamma ^2 k^2]}$ and $\frac{\partial ^2\pi _{ML}^R}{\partial w_N^2}= -\frac{4\beta \delta -\gamma ^2 k^2}{4(1-\delta )\beta \delta -\gamma ^2 k^2}<0$. By solving $\pi _{ML}^R=0$, we have $w_{NL}^{R*}= \frac{1+c_N}{2}-\frac{2\beta \delta (\delta -c_R)}{4\beta \delta -\gamma ^2 k^2}$.

Then we have

$$\begin{aligned} e_{L}^{R*}= & {} \frac{\gamma k(\delta -c_R)}{2(4\beta \delta -\gamma ^2k^2)}\\&+\frac{\gamma k(\delta c_N-c_R)}{2[4\beta \delta (1-\delta )-\gamma ^2k^2]}\\ p_{RL}^{R*}= & {} \frac{\delta (3+c_N)}{4}-\frac{(2\beta \delta -\gamma ^2k^2)(\delta -c_R)}{2(4\beta \delta -\gamma ^2k^2)}\\&-\frac{[2\beta \delta (1-\delta )-\gamma ^2k^2](\delta c_N-c_R)}{2[4\beta \delta (1-\delta )-\gamma ^2k^2]}\\ p_{RL}^{R*}= & {} \frac{\delta (1-c_N)+4c_R}{4}+\frac{(\delta -c_R)\beta \delta }{4\beta \delta -\gamma ^2k^2}\\&+\frac{(1-\delta )(\delta c_N-c_R)\beta \delta }{4\beta \delta (1-\delta )-\gamma ^2k^2}\\ p_{NL}^{R*}= & {} \frac{3+c_N}{4}-\frac{\beta \delta (\delta -c_R)}{4\beta \delta -\gamma ^2k^2}\\ \pi _{ML}^{R*}= & {} \frac{\{4(1-\delta +c_R-c_N)\beta \delta -\gamma ^2 k^2(1-c_N)\}^2}{8(4\beta \delta -\gamma ^2 k^2)[4(1-\delta )\beta \delta -\gamma ^2 k^2]} \end{aligned}$$

and

$$\begin{aligned} \pi _{RL}^{R*}= & {} \frac{(4\beta \delta {-}\gamma ^2k^2)^2(1{-}c_N)^2+8\beta (\delta {-}c_R)\{(4\beta \delta {-}\gamma ^2 k^2)[(1+c_N)\delta {-}2c_R]-6\beta \delta ^2(\delta {-}c_R)\}}{16[4(1{-}\delta )\beta \delta {-}\gamma ^2 k^2](4\beta \delta {-}\gamma ^2 k^2)}. \end{aligned}$$

1.10 Proof of Proposition 10

Assume $\delta p_N< p_R\le \delta p_N+ke$. Then:

$$\begin{aligned} \pi _{RM}^R= & {} \left\{ (1-\gamma )(1-p_N)+\gamma \left( 1-\frac{p_N-p_R+ke}{1-\delta }\right) \right\} (p_N-w_N)\\&+\left\{ \gamma \left( \frac{p_N-p_R+ke}{1-\delta }-\frac{p_R-ke}{\delta }\right) \right\} (p_R-c_R)-\beta e^2. \end{aligned}$$

With the same method in the case $0\le p_R\le \delta p_N$, the determinant of the Hessian can be written as: $|H|=\frac{\gamma \{4(1-\delta )\beta \delta -\gamma k^2\}}{(1-\delta )^2\delta ^2}>0$. Thus, we have get the green rate e the price of remanufactured product which can maximize the manufacturer’s and the retailer’s profit by solving $\frac{\partial \pi _{RM}^R}{\partial e}=0$ and $\frac{\partial \pi _{RM}^R}{\partial p_R}=0$, that are, $e=\frac{\gamma k(\delta w_N-\delta p_N+p_R-c_R)}{2(1-\delta )\beta \delta }$ and $p_R=\delta p_N+\frac{c_R-\delta w_N+ k e}{2}$. Solving the two equations together, we have

$$\begin{aligned} e=\frac{\gamma k(\delta w_N-c_R)}{4(1-\delta )\beta \delta -\gamma k^2} \end{aligned}$$

and

$$\begin{aligned} p_R=\delta p_N+\frac{(\delta w_N-c_R)[\gamma k^2-2(1-\delta )\beta \delta ]}{4(1-\delta )\beta \delta -\gamma k^2}. \end{aligned}$$

Substituting e and $p_R$ in to $\pi _{RM}^R$, then differentiating $\pi _{RM}^R$ with respect to $p_{N}$, we have

$$\begin{aligned} \frac{\partial \pi _{RM}^R}{\partial p_N}=1-2p_N+w_N \end{aligned}$$

and

$$\begin{aligned} \frac{\partial ^2 \pi _{RM}^R}{\partial p^2_N}=-2 \end{aligned}$$

As $\frac{\partial ^2 \pi _{RM}^R}{\partial p_N^2}<0$, we have $p_N$ which can maximize the profit by solving $\frac{\partial \pi _{MR}^R}{\partial p_N}=0$, that is,

$$\begin{aligned} p_N=\frac{1+w_N}{2}. \end{aligned}$$

Substituting $p_N$, e and $p_R$ into $\pi _{MM}^R$, and Differentiating $\pi _{MM}^R$ with respect to $w_{N}$, we have $\frac{\partial \pi _{MM}^R}{\partial w_N}=\frac{1}{2}-\frac{(2w_N-c_N)[4(1-\delta +\delta \gamma )\beta \delta -\gamma k^2]-4\beta \delta \gamma c_R}{2[4(1-\delta )\beta \delta -\gamma ^2 k^2]}$, $\frac{\partial ^2 \pi _{MM}^R}{\partial w^2_N}=-1-\frac{4\beta \delta ^2\gamma }{4(1-\delta )\beta \delta -\gamma k^2}<0$. By solving $\frac{\partial \pi _{MM}^R}{\partial w_N}=0$, then we have

$$\begin{aligned} w_{NM}^{R*}=\frac{1+c_N}{2}-\frac{2(\delta -c_R)\beta \delta \gamma }{4(1-\delta +\delta \gamma )\beta \delta -\gamma k^2}. \end{aligned}$$

In summary, we have the optimal decisions of the retailer and the manufacturer when $\delta p_N<p_R\le \delta p_N+ke$ are

$$\begin{aligned} e_M^{R*}= & {} \frac{\gamma k(\delta {-}c_R)}{2[4(1{-}\delta {+}\delta \gamma )\beta \delta {-}\gamma k^2]}\\&{+}\,\frac{\gamma k(\delta c_N{-}c_R)}{2[4\beta \delta (1{-}\delta ){-}\gamma k^2]}\\ p_{RM}^{R*}&{=}&\frac{\delta (3{+}c_N)}{4}{+}\frac{(\delta c_N{-}c_R)[\gamma k^2{-}2(1{-}\delta )\beta \delta ]}{2[4(1{-}\delta )\beta \delta {-}\gamma k^2]}\\&{-}\,\frac{(\delta {-}c_R)[2(1{-}\delta {+}\delta \gamma )\beta \delta {-}\gamma k^2]}{2[4(1{-}\delta {+}\delta \gamma )\beta \delta -\gamma k^2]}\\ p_{RM}^{R*}&{=}&\frac{\delta (1{-}c_N){+}4c_R}{4}{+}\frac{(\delta c_N{-}c_R)[(1{-}\delta )\beta \delta }{4(1{-}\delta )\beta \delta {-}\gamma k^2}\\&{+}\,\frac{(\delta {-}c_R)(1-\delta {+}\delta \gamma )\beta \delta }{4(1{-}\delta {+}\delta \gamma )\beta \delta {-}\gamma k^2}\\ p_{NM}^{R*}= & {} \frac{3{+}c_N}{4}{-}\frac{(\delta {-}c_R)\beta \delta \gamma }{4(1{-}\delta {+}\delta \gamma )\beta \delta {-}\gamma k^2}\\ \pi _{MM}^{R*}= & {} \frac{\{(1-c_N)[4(1{-}\delta )\beta \delta {-}\gamma k^2] {-}4(\delta c_N{-}c_R)\delta \gamma \beta \}^2}{8[4(1{-}\delta {+}\delta \gamma )\beta \delta {-}\gamma k^2][4(1{-}\delta )\beta \delta {-}\gamma k^2]}\\ \pi _{RM}^{R*}= & {} \frac{[4(1{-}\delta )\beta \delta {-}\gamma k^2]^2(1{-}c_N)^2{+}8\beta \gamma \{[4(1{-}\delta )\beta \delta {-}\gamma k^2][(2{-}c_N{+}c_N^2)\delta ^2{-}(3{+}c_N)\delta c_R{+}2c_R^2]{+}2(\delta c_N{-}c_R)^2\beta \delta ^2\gamma \}}{16[4(1{-}\delta {+}\delta \gamma )\beta \delta {-}\gamma k^2][4(1{-}\delta )\beta \delta {-}\gamma k^2]} \end{aligned}$$

1.11 Proof of Proposition 11

Assume $\delta p_N+ke<p_R\le p_N$, $\pi _{RH}^R=(1-p_N)(p_N-w_N)$, we can get $p_N$ which can maximize the profit by solving $\frac{\partial \pi _{RH}^R}{\partial p_N}=0$, that is,

$$\begin{aligned} p_N=\frac{1+w_N}{2}. \end{aligned}$$

Substituting $p_N$ into $\pi _{MH}^R$, we have

$$\begin{aligned} \pi _{MH}^R=\frac{(1-w_N)(w_N-c_N)}{2} \end{aligned}$$

By differentiating $\pi _{MH}^R$ with respect to $w_N$, we have

$$\begin{aligned} \frac{\partial \pi _{MH}^R}{\partial w_N}=-w_N+\frac{1+c_N}{2} \end{aligned}$$

and

$$\begin{aligned} \frac{\partial ^2 \pi _{MH}^R}{\partial w_N^2}=-1 \end{aligned}$$

As $\frac{\partial ^2\pi _{MH}^R}{\partial w_N^2}<0$, by solving $\frac{\partial \pi _{MH}^R}{\partial w_N}=0$, we have

$$\begin{aligned} w_{NH}^{R*}=\frac{1+c_N}{2} \end{aligned}$$

Substituting $w_{NH}^R$ into $\pi _{MH}^R$, the price of the new product is

$$\begin{aligned} p_{NH}^{R*}=\frac{3+c_N}{4} \end{aligned}$$

and the optimal profit of the manufacturer and the retailer are

$$\begin{aligned} \pi _{MH}^{R*}=\frac{(1-c_N)^2}{8} \end{aligned}$$

and

$$\begin{aligned} \pi _{RH}^{R*}=\frac{(1-c_N)^2}{16}. \end{aligned}$$

1.12 Proof of Proposition 12

$$\begin{aligned} \pi _{RL}^{R*}-\pi _{RH}^{R*}= & {} \frac{\beta \{(4\beta \delta -\gamma ^2 k^2)(\delta c_N-c_R)^2+3[4\beta \delta (1-\delta )-\gamma ^2 k^2](\delta -c_R)^2\}}{4(4\beta \delta -\gamma ^2 k^2)[4\beta \delta (1-\delta )-\gamma ^2 k^2]}>0\\ \pi _{RM}^{R*}-\pi _{RH}^{R*}= & {} \frac{\beta \gamma \{(4\beta \delta (1-\delta +\delta \gamma )-\gamma k^2)(\delta c_N-c_R)^2+3[4\beta \delta (1-\delta )-\gamma k^2](\delta -c_R)^2\}}{4[4\beta \delta (1-\delta )-\gamma k^2][4\beta \delta (1-\delta +\delta \gamma )-\gamma k^2]}>0 \end{aligned}$$

$\pi _{RL}^{R*}-\pi _{RM}^{R*}=\frac{\beta (1-\gamma )[4\beta \delta (1-\delta )-\gamma k^2-\gamma ^2 k^2]}{4}\left\{ \frac{(\delta c_N-c_R)^2}{[4\beta \delta (1-\delta )-\gamma k^2][4\beta \delta (1-\delta )-\gamma ^2 k^2]}\right. \left. +\frac{3(\delta -c_R)^2}{(4\beta \delta -\gamma ^2 k^2)[4\beta \delta (1-\delta +\delta \gamma )-\gamma k^2]}\right\}$. As $\gamma _1=\frac{\sqrt{16(1-\delta )\beta \delta +k^2}-k}{2k}$, it is easy to get $\frac{2(1-\delta )\beta \delta }{k^2}<\gamma _1<\min \left\{ \frac{4(1-\delta )\beta \delta }{k^2},\frac{\sqrt{2(1-\delta )\beta \delta }}{k}\right\}$. Then the Proposition is proved.

To avoid trivial calculations, we assume $0<\delta \le \frac{1-c_N^2}{1+c_N^2}$ under the comparisons of the manufacturer’s profits in different pricing strategies.

As $\pi _{ML}^{R*}-\pi _{MH}^{R*}=\frac{\beta \delta \{4\beta \delta (\delta -c_R)^2-(4\beta \delta -\gamma ^2 k^2)(1-c_N)(\delta c_N+\delta -2c_R)\}}{2(4\beta \delta -\gamma ^2 k^2)[4\beta \delta (1-\delta )-\gamma ^2 k^2]}$, denoting $I=4\beta \delta (\delta -c_R)^2-(4\beta \delta -\gamma ^2 k^2)(1-c_N)(\delta c_N+\delta -2c_R)$, we can find I has the same symbol with $\pi _{ML}^{R*}-\pi _{MH}^{R*}$. Furthermore I is a convex function of $\gamma$, by solving $I=0$ with $\gamma >0$, we have the threshold ${{\hat{\gamma }}}=2\sqrt{\frac{\beta \delta \{(1-c_N)(\delta c_N+\delta -2c_R)-(\delta -c_R)^2\}}{(1-c_N)(\delta c_N+\delta -2c_R)k}}$. Then we compare ${{\hat{\gamma }}}$ with $\min \left\{ \frac{4(1-\delta )\beta \delta }{k^2},\frac{\sqrt{2(1-\delta )\beta \delta }}{k}\right\}$.

• (i) When $2\sqrt{(1-\delta )\beta \delta }<k<2\sqrt{2(1-\delta )\beta \delta }$, by comparing ${{\hat{\gamma }}}$ with $\frac{\sqrt{2(1-\delta )\beta \delta }}{k}$, we have ${\hat{\gamma }}^2-\left( \frac{\sqrt{2(1-\delta )\beta \delta }}{k}\right) ^2=\frac{2\beta \delta \{-2c_R^2+2(\delta c_N+\delta +c_N-1)c_R+\delta (1-\delta -\delta c_N^2-c_N^2)\}}{(1-c_N)(\delta c_N+\delta -2c_R)k^2}$. Denoting $T=-2c_R^2+2(\delta c_N+\delta +c_N-1)c_R+\delta (1-\delta -\delta c_N^2-c_N^2)$, ${\hat{\gamma }}^2-\left( \frac{\sqrt{2(1-\delta )\beta \delta }}{k}\right) ^2$ has same symbol with T. As T is a continuous and concave function of $c_R$, with the assumption $0<\delta \le \frac{1-c_N^2}{1+c_N^2}$ and $c_R<\delta c_N$ we have $T|_{c_R=0}=\delta (1-\delta -\delta c_N^2-c_N^2)\ge 0$ and $T|_{c_R=\delta c_N}=\delta (1-\delta )(1-c_N)^2>0$. Thus we can conclude ${\hat{\gamma }}\ge \frac{\sqrt{2(1-\delta )\beta \delta }}{k}$.

• (ii) When $k\ge 2\sqrt{2(1-\delta )\beta \delta }$, by comparing ${{\hat{\gamma }}}$ with $\frac{4(1-\delta )\beta \delta }{k^2}$, we have

  ${\hat{\gamma }}^2-\left( \frac{4(1-\delta )\beta \delta }{k^2}\right) ^2=\frac{4\beta \delta \{[(1-c_N)(\delta c_N+\delta -2c_R)-(\delta -c_R)^2]k^2-4\beta \delta (1-\delta )^2(1-c_N)(\delta c_N+c_N-2c_R)\}}{(1-c_N)(\delta c_N+\delta -2c_R)k^4}$. With $0<\delta \le \frac{1-c_N^2}{1+c_N^2}$ and $c_R<\delta c_N$, we can prove $(1-c_N)(\delta c_N+\delta -2c_R)-(\delta -c_R)^2$ is positive and ${\hat{\gamma }}^2-\left( \frac{4(1-\delta )\beta \delta }{k^2}\right) ^2$ is increasing in k. With same approach, we have ${{\hat{\gamma }}^2-\left( \frac{4(1-\delta )\beta \delta }{k^2}\right) ^2}|_{k=2\sqrt{2(1-\delta )\beta \delta }}>0$. Thus we can conclude ${{\hat{\gamma }}}-\frac{4(1-\delta )\beta \delta }{k^2}>0$. Then we have I is negative in $\frac{2(1-\delta )\beta \delta }{k^2}<\gamma <\min \left\{ \frac{4(1-\delta )\beta \delta }{k^2},\frac{\sqrt{2(1-\delta )\beta \delta }}{k}\right\}$ with the assumption $0<\delta \le \frac{1-c_N^2}{1+c_N^2}$. Thus, we can conclude $\pi _{ML}^{R*}-\pi _{MH}^{R*}\le 0$.

As $\pi _{MM}^{R*}-\pi _{MH}^{R*}=\frac{\beta \delta \gamma \{4\beta \delta \gamma (\delta c_N-c_R)^2-(4\beta \delta (1-\delta )-\gamma k^2)(1-c_N)(\delta c_N+\delta -2c_R)\}}{2[4\beta \delta (1-\delta )-\gamma k^2][4\beta \delta (1-\delta +\delta \gamma )-\gamma k^2]}$, with same method with $\pi _{ML}^{R*}-\pi _{MH}^{R*}$ and denoting $X=4\beta \delta \gamma (\delta c_N-c_R)^2-(4\beta \delta (1-\delta )-\gamma k^2)(1-c_N)(\delta c_N+\delta -2c_R)$, by solving $X=0$, we have $\gamma _2=\frac{4\beta \delta (1-\delta )(1-c_N)(\delta c_N+\delta -2c_R)}{(1-c_N)(\delta c_N+\delta -2c_R)k^2+4\beta \delta (\delta c_N-c_R)^2}$. We can easily prove $\frac{2(1-\delta )\beta \delta }{k^2}<\gamma _2\le \frac{4(1-\delta )\beta \delta }{k^2}$. Thus, we have $\pi _{MM}^{R*}<\pi _{MH}^{R*}$ when $\frac{2(1-\delta )\beta \delta }{k^2}<\gamma <\gamma _2$; $\pi _{MM}^{R*}\ge \pi _{MH}^{R*}$ when$\gamma _2\le \gamma <\frac{4(1-\delta )\beta \delta }{k^2}$.

In summary, we can conclude that $\pi _{MM}^{R*}<\pi _{MH}^{R*}$ when $\frac{2(1-\delta )\beta \delta }{k^2}<\gamma <\gamma _2$; $\pi _{MM}^{R*}\ge \pi _{MH}^{R*}$ when$\gamma _2\le \gamma <\frac{4(1-\delta )\beta \delta }{k^2}$, the manufacture will not use low price strategy.

1.13 Proof of Proposition 13

• (i) As $c_R<\delta c_N<\delta$, we have $p_N^{C**}-p_{NM}^{R**}=\frac{[4(1-\delta +\delta \gamma )\beta \delta -\gamma k^2]c_N-[4(1-\delta +\gamma c_R)\beta \delta -\gamma k^2]}{4[4(1-\delta +\delta \gamma )\beta \delta -\gamma k^2]}<-\frac{1-c_N}{4}<0$. In addition, it is easy to prove $p_N^{C**}<p_{NH}^{R**}$, $p_N^{C**}<p_N^{M**}$ and $p_N^{R**}\le p_N^{M**}$. Thus we can conclude that $p_N^{C**}<p_N^{R**}\le p_N^{M**}$.

• (ii) $w_N^{M**}-w_{NM}^{R**}=\frac{(\delta c_N-c_R)\gamma k}{4(1-\delta +\delta \gamma )\beta \delta -\gamma k^2}>0$ and $w_N^{M**}=w_{NH}^{R**}$, then we get $w_N^{M**}\ge w_{N}^{R**}$.

1.14 Proof of Proposition 14

(ii) $e^{M**}-e_L^{C**}=-\frac{4(1-\delta )(\delta c_N-c_R)\gamma k\beta \delta }{[4(1-\delta )\beta \delta -\gamma ^2 k^2][8(1-\delta )\beta \delta -\gamma ^2 k^2]}<0$ and $e^{M**}-e_M^{C**}=-\frac{(\delta c_N-c_R)[4(1-\delta )\beta \delta +\gamma k^2-\gamma ^2 k^2]\gamma k}{[4(1-\delta )\beta \delta -\gamma k^2][8(1-\delta )\beta \delta -\gamma ^2 k^2]}<0$, then we an conclude that $e^{M**}<e^{C**}$.