Skip to main content

Advertisement

Springer Nature Link
Log in

Enhancing the predictive performance of ensemble models through novel multi-objective strategies: evidence from credit risk and business model innovation survey data

  • Original Research
  • Published:
Annals of Operations Research Aims and scope Submit manuscript

Abstract

This paper proposes novel multi-objective optimization strategies to develop a weighted ensemble model. The comparison of the performance of the proposed strategies against simulated data suggests that the multi-objective strategy based on joint entropy is superior to other proposed strategies. For the application, generalization, and practical implications of the proposed approaches, we implemented the model on two real datasets related to the prediction of credit risk default and the adoption of the innovative business model by firms. The scope of this paper can be extended in ordering the solutions of the proposed multi-objective strategies and can be generalized for other similar predictive tasks.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

Notes

  1. Business model innovation refers to changes in the existing structure of assets and operations (i.e., business model) that a company uses to deal with the market. Whether a firm at strategic level realizes this or not, business model is always there, which could be either in evident or latent form. In principle, the underlying logic or architecture of any business always refers to the business model in place. A firm changes many decisions at strategic level across various functions which may lead to the overall innovation of the existing business model. Specifically, it is the combination of several changes in different functions of business which matters the most in innovating the business model. The design of the survey is done in such a way to capture information of the changes done across different functions within the firm. Such integrated changes of different functions in the business most likely lead to innovation of the business model. In abstract sense, the binary dependent variable “business model innovation” is nothing but a function of individual indicators that refers changes in the business model. More precisely, business model innovation is a function BMI = f (f3, p7, f2, n5, ...), which is a linear combination of individual indicators of business model change. We thank an anonymous referee for helping to make this point clearer.

  2. For credit risk dataset, the class size, their distribution after SMOTE are (9342, 10,899) and (46%, 54%) respectively. For business model dataset, the class size, their distribution after SMOTE are (1881, 2037) and (48%, 52%) respectively.

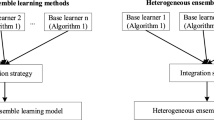
  3. EMM1 refers the proposed strategy 3, EMM2 to strategy 4, EMM3 to strategy 2, and EMM4 to strategy 1. EMS1, EMS2, EMS3 and EMS4 refers to the single-objective optimization function of the proposed four strategies and follows the same sequence of EMM1, EMM2, EMM3, and EMM4.

  4. EMM2 refers to the proposed multiobjective strategy 3 and EMS2 is a single-objective version of EMM2. EMM2 and EMM1 are interchangeably the same as they have been developed using strategy 3, it is just two different convention for evaluating the performance on two different datasets.So, is the case with EMS1 and EMS2. The other models in Table 4 stands for GLM(generalized linear model), RF(random forest), and BMA(Bayesian moving average).

References

  • Bäck, T. (1996). Evolutionary algorithms in theory and practice: Evolution strategies, evolutionary programming, genetic algorithms. Oxford University Press.

  • Banner, K. M., & Higgs, M. D. (2017). Considerations for assessing model averaging of regression coefficients. Ecological Applications, 27, 78–93.

    Article  Google Scholar 

  • Belton, V., & Stewart, T. (2002). Multiple criteria decision analysis: An integrated approach. Springer.

  • Breskvar, M., Kocev, D., & Džeroski, S. (2018). Ensembles for multi-target regression with random output selections. Machine Learning, 107, 1673–1709.

    Article  Google Scholar 

  • Burnham, K., & Anderson, D. R. (2002). Model selection and multi-model inference: A practical information-theoretic approach. Springer, 26(2), 1–488.

    Google Scholar 

  • Chawla, Nitesh V., Bowyer, Kevin W., Hall, Lawrence O., & Philip Kegelmeyer, W. (2002). SMOTE: Synthetic Minority Over-sampling Technique. Journal of Artificial Intelligence Research, 16, 321–57.

    Article  Google Scholar 

  • Coello, C. A. C., Lamont, G. B., & Van Veldhuizen, D. A. (2007). Evolutionary algorithms for solving multiobjective problems. Springer.

  • Deb, K. (2001). Multiobjective optimization using evolutionary algorithms (pp. 1–518). Wiley.

  • Deb, K. (2001). Multiobjective optimization using evolutionary algorithms. Wiley.

  • Dellnitz, M., Schutze, O., & Hestermeyer, T. (2005). Covering pareto sets by multilevel subdivison techniques. Journal of Optimization Theory and Applications, 124(1), 113–136.

    Article  Google Scholar 

  • DeLong, E. R., DeLong, D. M., & Clarke-Pearson, D. L. (1988). Comparing the areas under two or more correlated receiver operating characteristic curves: a nonparametric approach. Biometrics, 837–845.

  • Ehrgott, M. (2005). Multicriteria optimization. Springer.

  • Ehrgott, M. (2012). Vilfredo Pareto and multiobjective optimization. Optimization stories. Journal der Deutschen Mathematiker-Vereininggung, Extra, 21, 447–453.

    Google Scholar 

  • Fletcher, S., Verma, B., & Zhang, M. (2020). A non-specialized ensemble classifier using multi-objective optimization. Neurocomputing, 409, 93–102.

    Article  Google Scholar 

  • Ignizio, J. P. (1976). Goal programming and extensions. Lexington Books.

  • Izui, K., Yamada, T., Nishiwaki, S., & Tanaka, K. (2015). Multiobjective optimization using an aggregative gradient-based method. Structural and Multidisciplinary Optimization, 51, 173–182.

    Article  Google Scholar 

  • Jin, Y. (2006). Multi-objective machine learning (Vol. 14, pp. 1–660). Springer.

  • Jürgen, B., Kalyanmoy, D., Kaisa, M., & Roman, S. (2008). Multiobjective optimization: Interactive and evolutionary approaches. Springer.

  • Kordík, P., Černý, J., & Frýda, T. (2018). Discovering predictive ensembles for transfer learning and meta-learning. Machine Learning, 107, 177–207.

    Article  Google Scholar 

  • Kou, G., Peng, Y., & Wang, G. (2014). Evaluation of clustering algorithms for financial risk analysis using MCDM methods. Information Sciences, 275, 1–12.

    Article  Google Scholar 

  • Kou, G., Xu, Y., Peng, Y., Shen, F., Chen, Y., Chang, K., & Kou, S. (2021). Bankruptcy prediction for SMEs using transactional data and two-stage multiobjective feature selection. Decision Support Systems, 140, 113429.

    Article  Google Scholar 

  • Kou, G., Xiao, H., Cao, M., & Lee, L. H. (2021). Optimal computing budget allocation for the vector evaluated genetic algorithm in multi-objective simulation optimization. Automatica, 129, 109599.

    Article  Google Scholar 

  • Kozodoi, N., Lessmann, S., Papakonstantinou, K., Gatsoulis, Y., & Baesens, B. (2019). A multi-objective approach for profit-driven feature selection in credit scoring. Decision Support Systems, 120, 106–117.

    Article  Google Scholar 

  • Krawczyk, B. (2016). Learning from imbalanced data: Open challenges and future directions. Progress in Artificial Intelligence, 5(4), 221–232.

    Article  Google Scholar 

  • Kuncheva, L., & Whitaker, C. (2003). Measures of diversity in classifier ensembles and their relationship with the ensemble accuracy’’. Machine Learning, 51(2), 181–207.

    Article  Google Scholar 

  • Li, T., Kou, G., Peng, Y., & Yu, P. S. (2021). An integrated cluster detection, optimization, and interpretation approach for financial data. IEEE Transactions on Cybernetics, 1–14.

  • Mackay, D. J. C. (2003). Information theory, inferences, and learning algorithms. Cambridge University Press.

  • Murphy, K. (2012). Machine learning: A probabilistic perspective. MIT Press.

  • Peimankar, A., Weddell, S. J., Jalal, T., & Lapthorn, A. C. (2018). Multi-objective en- semble forecasting with an application to power transformers. Applied Soft Computing, 68, 233–248.

    Article  Google Scholar 

  • Ribeiro, V. H. A., & Meza, G. R. (2020). Ensemble learning by means of a multi-objective optimization design approach for dealing with imbalanced data sets. Expert Systems with Applications, 147, 113–232.

    Google Scholar 

  • Rosales-Perez, A., Garcia, S., Gonzalez, J. A., Coello, C. A. C., & Herrera, F. (2017). An evolutionary multi-objective model and instance selection for support vector machines with Pareto–based ensembles. IEEE Transactions on Evolutionary Com- putation, 1.

  • Sahâ, S., Sarkar, D., & Kramer, S. (2019). Exploring multi-objective optimization for multi-label classifier ensembles. IEEE Congress on Evolutionary Computation (CEC), 2019, 2753–2760.

    Google Scholar 

  • Shi, C., Kong, X., Fu, D., Yu, P. S., & Wu, B. (2014). Multi-label classification based on multi-objective optimization. Association for Computing Machinery, 5(2), 1–22.

    Google Scholar 

  • Smith, C., & Jin, Y. (2014). Evolutionary multi-objective generation of recurrent neu- ral network ensembles for time series prediction. Neurocomputing, 143, 302–311.

    Article  Google Scholar 

  • Tan, C. J., Lim, C. P., & Cheah, Y. N. (2014). A multi-objective evolutionary algorithm- based ensemble optimizer for feature selection and classification with neural network models. Neurocomputing, 125, 217–228.

    Article  Google Scholar 

  • Tumer, K., & Ghosh, J. (1996). Analysis of decision boundaries in linearly combined neural classifiers. Pattern Recognition, 29(2), 341–348.

    Article  Google Scholar 

  • Wang, W., et al. (2019). An effective ensemble framework for multiobjective optimization. IEEE Transactions on Evolutionary Computation, 23(4), 645–659.

    Article  Google Scholar 

  • Wang, F., Li, Y., Liao, F., & Yan, H. (2020). An ensemble learning based prediction strategy for dynamic multi-objective optimization. Applied Soft Computing, 96, 106592.

    Article  Google Scholar 

  • Wozniak, M., Graña, M., & Corchado, E. (2014). A survey of multiple classifier systems as hybrid systems. Information Fusion, 16, 3–17.

    Article  Google Scholar 

  • Zhang, C., & Yunqian, M. (2012). Ensemble machine learning: Methods and applications. Springer.

  • Zhao, J., Jiao, L., Xia, S., Basto Fernandes, V., Yevseyeva, I., Zhou, Y., Emmerich, T. M., & M. (2018). Multiobjective sparse ensemble learning by means of evolutionary algorithms. Decision Support Systems,111, 86–100. https://doi.org/10.1016/j.dss.2018.05.003

  • Zhao, H. (2007). A multi-objective genetic programming approach to developing Pareto optimal decision trees. Decision Support Systems, 43(3), 809–826.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Economics and Management, University of Bergamo, Bergamo, Italy

    Paritosh Jha

  2. Department of Economics and Social Sciences, Marche Polytechnic University, Ancona, Italy

    Marco Cucculelli

Authors
  1. Paritosh Jha
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Marco Cucculelli
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Paritosh Jha.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

1.1 Details on credit risk dataset

See Tables 5, 6, 7 and 8.

Table 5 Socio-economic variable description
Full size table
Table 6 Client equipment variable description
Full size table
Table 7 Client history variable description
Full size table
Table 8 Client behavior variable description
Full size table

1.2 Details on business model innovation dataset

See Table 9

Table 9 Variable description of business model innovation dataset
Full size table

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Jha, P., Cucculelli, M. Enhancing the predictive performance of ensemble models through novel multi-objective strategies: evidence from credit risk and business model innovation survey data. Ann Oper Res 325, 1029–1047 (2023). https://doi.org/10.1007/s10479-022-05028-0

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10479-022-05028-0

Keywords