Contracts for online retailers considering consumer intra-product showrooming

Abstract

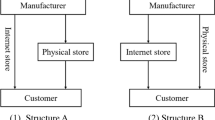
Given the proliferation of platform retailing in recent years, there is a need to understand the conditions under which online retailers would adopt a revenue-sharing or fixed-fee contract. We consider a setting in which a manufacturer distributes a single product to consumers through two channels: an online intermediary marketplace operated by an online retailer and a manufacturer-owned brick-and-mortar store. This article focuses on studying the online retailer’s contract choice in the presence of intra-product showrooming. Our analysis shows that there is no dominating contract that the online retailer always prefers. We characterize the parameter ranges for each equilibrium scenario. Moreover, we investigate the effect of service cost on the online retailer’s and manufacturer’s profits and find that the online retailer’s profit is negatively affected by the costly service, whereas the manufacturer could benefit from service cost under certain conditions. Our analysis further reveals that the price is higher under a fixed-fee contract than under a revenue-sharing contract. We conclude that the online retailer can adjust the contract parameters appropriately to induce the desired service level and price, and the manufacturer can devise his strategies more effectively to enhance the overall profits. We also extend our framework to encompass richer functional form of the cost of service, differentiated channels, as well as offline shopping costs and online returns.

Appendix

1.1 Proof of Theorem 1

Given commission rate $\lambda$, the first-order condition of the manufacturer’s objective function (Equation (1)) with respect to p is $s(1-\frac{\lambda }{2}-2p+\lambda p)=0$, and the first-order condition with respect to s is $p(1-\frac{\lambda }{2}-p+\frac{\lambda p}{2})-2ks=0$. To make a profit, the manufacturer has to set $s>0$ in his BM store. Thus, for any positive s, the first-order conditions yield $p=\frac{1}{2}$, which in turn yields optimal $s=\frac{2- \lambda }{16k}$. Note that the value of s is bounded by 1. When $\frac{2- \lambda }{16k}<1$, the Hessian matrix

$$\begin{aligned} \left[ \begin{array}{cc} \frac{\partial ^2 \pi _{m}(p,s)}{\partial p^2} &{} \frac{\partial ^2 \pi _{m}(p,s)}{\partial p\partial s}\\ \frac{\partial ^2 \pi _{m}(p,s)}{\partial s \partial p} &{} \frac{\partial ^2 \pi _{m}(p,s)}{\partial s^2} \end{array} \right] = \left[ \begin{array}{cc} -s(2-\lambda ), &{} 1-\frac{\lambda }{2}-2p+\lambda p\\ 1-\frac{\lambda }{2}-2p+\lambda p, &{} -2k \end{array} \right] = \left[ \begin{array}{cc} -s(2-\lambda ), &{} 0\\ 0, &{} -2k \end{array} \right] \end{aligned}$$

is negative definite at $p=\frac{1}{2}$ and $s=\frac{2- \lambda }{16k}$, implying that the maximum expected profit is achieved at this point. However, when $\frac{2- \lambda }{16k}\ge 1$, the condition $s\le 1$ is binding. By comparing the first-order derivative of the profit function with respect to s, $p(1-\frac{\lambda }{2}-p+\frac{\lambda p}{2})-2ks=\frac{1}{2}(\frac{1}{2}-\frac{\lambda }{4})-2ks$, to zero, we derive that it is optimal to set the corner solution as $s=1$. Thus, the optimal decision for the manufacturer is to set the price at $p=\frac{1}{2}$, and the service level at $s=\min \{1,\frac{2- \lambda }{16k}\}$. Specifically, $s=1$ if $\lambda \le 2-16k$ and $s=\frac{2- \lambda }{16k}$ if $\lambda >2-16k$. In both cases, the online retailer’s profit function is given by $\pi _r(\lambda )=\frac{s(1-p)p\lambda }{2}$. Using the values of p and s solved above, the online retailer’s and manufacturer’s profits can be written as

$$\begin{aligned} \pi _r=\left\{ \begin{array}{ll} \frac{\lambda }{8}, &{}\hbox {if}\, \lambda \le 2-16k\\ \frac{(2-\lambda )\lambda }{128k}, &{}\hbox {if}\, \lambda >2-16k, \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} \pi _m=\left\{ \begin{array}{ll} \frac{2-8k-\lambda }{8}, &{}\hbox {if}\, \lambda \le 2-16k\\ \frac{(-2+\lambda )^2}{256k}, &{}\hbox {if}\, \lambda >2-16k. \end{array} \right. \end{aligned}$$

There are two cases to consider. Case 1: Under the condition of $\lambda \le 2-16k$, if $2-16k\ge \overline{\lambda }$, that is, $k\le \frac{1}{8}-\frac{\overline{\lambda }}{16}$, the optimal commission rate is $\lambda =\overline{\lambda }$, and hence $\pi _r=\frac{\overline{\lambda }}{8}$ and $\pi _m=\frac{2-8k-\overline{\lambda }}{8}$. If $0\le 2-16k<\overline{\lambda }$, that is, $\frac{1}{8}-\frac{\overline{\lambda }}{16}<k\le \frac{1}{8}$, the optimal commission rate is $\lambda =2-16k$, and hence $\pi _r=\frac{2-16k}{8}$ and $\pi _m=k$. Case 2: Under the condition of $\lambda >2-16k$, if $2-16k<\overline{\lambda }$, that is, $\frac{1}{8}-\frac{\overline{\lambda }}{16}<k$, the optimal commission rate is $\lambda =\overline{\lambda }$, and hence $\pi _r=\frac{(2-\overline{\lambda })\overline{\lambda }}{128k}$ and $\pi _m=\frac{(-2+\overline{\lambda })^2}{256k}$. According to the analysis above, we note that when $\frac{1}{8}-\frac{\overline{\lambda }}{16}<k\le \frac{1}{8}$, the online retailer has two choices: one is to choose $\lambda =2-16k$, and then her profit is $\pi _r=\frac{2-16k}{8}$; and the other one is to choose $\lambda =\overline{\lambda }$ and then her profit is $\pi _r=\frac{(2-\overline{\lambda })\overline{\lambda }}{128k}$. Between these two choices, the online retailer chooses the one under which she is better off. The difference between the two profits is $\frac{2-16k}{8}-\frac{(2-\overline{\lambda })\overline{\lambda }}{128k}=\frac{1}{128k}(32k-256k^2-\overline{\lambda }(2-\overline{\lambda }))<0.$ Thus, under the condition of $\frac{1}{8}-\frac{\overline{\lambda }}{16}<k\le \frac{1}{8}$, the online retailer would choose $\lambda =\overline{\lambda }$ and then her profit is $\pi _r=\frac{(2-\overline{\lambda })\overline{\lambda }}{128k}$. This completes the proof of Theorem 1.

1.2 Proof of Theorem 2

In the second stage, the manufacturer sets the price and service level. The first-order condition of the manufacturer’s objective function (Equation (2)) with respect to p is $s(1-2p+\frac{r}{2})=0$, and the first-order condition with respect to s is $(p-\frac{r}{2})(1-p)-2ks=0$. To make a profit, the manufacturer has to set $s>0$ in his BM store. Thus, for any positive s, the first-order conditions yield $p=\frac{1}{2}+\frac{r}{4}$, which in turn yields optimal $s=\frac{(\frac{1}{2}-\frac{r}{4})^2}{2k}$. Note that the equilibrium service level s is bounded by the feasibility condition $0\le s\le 1$. When $\frac{(\frac{1}{2}-\frac{r}{4})^2}{2k}<1$, the Hessian matrix

$$\begin{aligned} \left[ \begin{array}{cc} \frac{\partial ^2 \pi _{m}(p,s)}{\partial p^2} &{} \frac{\partial ^2 \pi _{m}(p,s)}{\partial p\partial s}\\ \frac{\partial ^2 \pi _{m}(p,s)}{\partial s \partial p} &{} \frac{\partial ^2 \pi _{m}(p,s)}{\partial s^2} \end{array} \right] = \left[ \begin{array}{cc} -2s, &{} 1-2p+\frac{r}{2}\\ 1-2p+\frac{r}{2}, &{} -2k \end{array} \right] = \left[ \begin{array}{cc} -2s, &{} 0\\ 0, &{} -2k \end{array} \right] \end{aligned}$$

is negative definite at $p=\frac{1}{2}+\frac{r}{4}$ and $s=\frac{(\frac{1}{2}-\frac{r}{4})^2}{2k}$, implying that the maximum expected profit is achieved at this point. When $\frac{(\frac{1}{2}-\frac{r}{4})^2}{2k}\ge 1$, however, the condition $s\le 1$ is binding. By comparing the first-order derivative of the profit function with respect to s, $(p-\frac{r}{2})(1-p)-2ks=(\frac{1}{2}-\frac{r}{4})^2-2ks$, to zero, we know that it is optimal to set the corner solution as $s=1$. Thus, the manufacture’s optimal decision is to set the price at $p=\frac{1}{2}+\frac{r}{4}$, and the service level at $s=\min \{1,\frac{(\frac{1}{2}-\frac{r}{4})^2}{2k}\}$. Specifically, $s=1$ if $r\le 2-4\sqrt{2k}$ and $s=\frac{(\frac{1}{2}-\frac{r}{4})^2}{2k}$ if $2-4\sqrt{2k}<r\le \overline{r}$. In both cases, the online retailer’s profit function is given by $\pi _r(r)=\frac{s(1-p)r}{2}$. Using the values of p and s solved above, the online retailer’s and manufacturer’s profits can be written as

$$\begin{aligned} \pi _r=\left\{ \begin{array}{ll} \frac{2r-r^2}{8}, &{}\hbox {if}\, r\le 2-4\sqrt{2k}\\ \frac{(\frac{1}{2}-\frac{r}{4})^3r}{4k}, &{}\hbox {if}\, 2-4\sqrt{2k}<r\le \overline{r}, \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} \pi _m=\left\{ \begin{array}{ll} \frac{4-16k-4r+r^2}{16}, &{}\hbox {if}\, r\le 2-4\sqrt{2k}\\ \frac{(-2+r)^4}{1024k}, &{}\hbox {if}\, 2-4\sqrt{2k}<r\le \overline{r}. \end{array} \right. \end{aligned}$$

There are two cases to consider. Case 1: Under the condition of $r\le 2-4\sqrt{2k}$, if $2-4\sqrt{2k}\ge \overline{r}$, that is, $k\le \frac{(2-\overline{r})^2}{32}$, the optimal fixed rent is $r=\overline{r}$, and hence $\pi _r=\frac{2\overline{r}-\overline{r}^2}{8}$ and $\pi _m=\frac{4-16k-4\overline{r}+\overline{r}^2}{16}$. If $0\le 2-4\sqrt{2k}<\overline{r}$, that is, $\frac{(2-\overline{r})^2}{32}<k\le \frac{1}{8}$, the optimal fixed rent is $r=2-4\sqrt{2k}$, and hence $\pi _r=\sqrt{2k}-4k$ and $\pi _m=k$. Case 2: Under the condition of $2-4\sqrt{2k}<r\le \overline{r}$, which implies that $\frac{(2-\overline{r})^2}{32}<k$, we have that (i) if $\frac{(2-\overline{r})^2}{32}<k$ and $\overline{r}< \frac{1}{2}$, the optimal fixed rent is $r=\overline{r}$, and hence $\pi _r=\frac{(2-\overline{r})^3\overline{r}}{256k}$ and $\pi _m=\frac{(2-\overline{r})^4}{1024k}$; (ii) if $2-4\sqrt{2k}<\frac{1}{2}$ (i.e., $\frac{9}{128}<k$) and $\frac{1}{2}\le \overline{r}$, the optimal fixed rent is $r=\frac{1}{2}$, and hence $\pi _r=\frac{27}{4096k}$ and $\pi _m=\frac{81}{16384k}$; and (iii) if $\frac{(2-\overline{r})^2}{32}<k\le \frac{9}{128}$ and $\frac{1}{2}\le \overline{r}$, the optimal fixed rent is $r=2-4\sqrt{2k}$, and hence $\pi _r=\sqrt{2k}-4k$ and $\pi _m=k$.

According to the analysis above, we note that when $\frac{(2-\overline{r})^2}{32}<k\le \frac{1}{8}$ and $\overline{r}< \frac{1}{2}$, the online retailer has two choices: one is to choose $r=2-4\sqrt{2k}$ and then her profit is $\pi _r=\sqrt{2k}-4k$; and the other is to choose $r=\overline{r}$ and then her profit is $\pi _r=\frac{(2-\overline{r})^3\overline{r}}{256k}$. Between these two choices, the online retailer chooses that under which she is better off. Because $\frac{(2-\overline{r})^3\overline{r}}{256k}-\sqrt{2k}+4k\ge 0$, the online retailer would choose $r=\overline{r}$ and then her profit is $\pi _r=\frac{(2-\overline{r})^3\overline{r}}{256k}$. When $\frac{(2-\overline{r})^2}{32}<k\le \frac{9}{128}$ and $\frac{1}{2}\le \overline{r}$, the optimal fixed rent is $r=2-4\sqrt{2k}$, and hence $\pi _r=\sqrt{2k}-4k$ and $\pi _m=k$. When $\frac{9}{128}<k$ and $\frac{1}{2}\le \overline{r}$, the optimal fixed rent is $r=\frac{1}{2}$, and hence $\pi _r=\frac{27}{4096k}$ and $\pi _m=\frac{81}{16384k}$. This completes the proof of Theorem 2.

1.3 Proof of Proposition 1

From the results in Table 1, when $k \le \frac{1}{8}-\frac{\overline{\lambda }}{16}$, we have that the online retailer’s profit is $\frac{\overline{\lambda }}{8}$, and when $k > \frac{1}{8}-\frac{\overline{\lambda }}{16}$, we have that the online retailer’s profit is $\frac{(2-\overline{\lambda })\overline{\lambda }}{128k}$. From the results in Table 2, when $k\le \frac{(2-\overline{r})^2}{32}$, we have that the online retailer’s profit is $\frac{2\overline{r}-\overline{r}^2}{8}$, when $\frac{(2-\overline{r})^2}{32}<k$ and $\overline{r}< \frac{1}{2}$, we have that the online retailer’s profit is $\frac{(2-\overline{r})^3\overline{r}}{256k}$, when $\frac{(2-\overline{r})^2}{32}<k\le \frac{9}{128}$ and $\frac{1}{2}\le \overline{r}$, we have that the online retailer’s profit is $\sqrt{2k}-4k$, and when $\frac{9}{128}<k$ and $\frac{1}{2}\le \overline{r}$, we have that the online retailer’s profit is $\frac{27}{4096k}$.

Next we compare the above-defined results to present the online retailer’s equilibrium profits under the revenue-sharing and fixed-fee contracts and determine the online retailer’s equilibrium choice of contract. We first consider the case with $2\overline{r} - \frac{\overline{r}^2}{2} \le \overline{\lambda }$. In this case, since $\overline{\lambda }\le 1$, we have $\overline{r}\le 2 - \sqrt{2}$. In this case, when $k\le \frac{1}{8}-\frac{\overline{\lambda }}{16}$, we have $\pi _r(\lambda ) - \pi _r(r) = \frac{\overline{\lambda }}{8} - \frac{2\overline{r}-\overline{r}^2}{8} \ge \frac{2\overline{r} - \frac{\overline{r}^2}{2}}{8} - \frac{2\overline{r}-\overline{r}^2}{8} = \frac{\overline{r}^2}{16} \ge 0$. Thus, when $k\le \frac{1}{8}-\frac{\overline{\lambda }}{16}$, the online retailer prefers the revenue-sharing contract to the fixed-fee contract and her profit is $\frac{\overline{\lambda }}{8}$. When $\frac{1}{8}-\frac{\overline{\lambda }}{16} < k \le \frac{(2-\overline{r})^2}{32}$, we have $\pi _r(\lambda ) - \pi _r(r) = \frac{(2-\overline{\lambda })\overline{\lambda }}{128k} - \frac{2\overline{r}-\overline{r}^2}{8} \ge \frac{(2-\overline{\lambda })\overline{\lambda }}{128\cdot \frac{(2-\overline{r})^2}{32}} - \frac{2\overline{r}-\overline{r}^2}{8} \ge \frac{(2-(2\overline{r} - \frac{\overline{r}^2}{2}))(2\overline{r} - \frac{\overline{r}^2}{2})}{4 (2-\overline{r})^2} - \frac{2\overline{r}-\overline{r}^2}{8} = \frac{\overline{r}^2}{16} \ge 0$. Thus, when $\frac{1}{8}-\frac{\overline{\lambda }}{16} < k \le \frac{(2-\overline{r})^2}{32}$, the online retailer prefers the revenue-sharing contract to the fixed-fee contract and her profit is $\frac{(2-\overline{\lambda })\overline{\lambda }}{128k}$. When $\frac{(2-\overline{r})^2}{32} < k$ and $\overline{r} < \frac{1}{2}$, we have $\pi _r(\lambda ) - \pi _r(r) = \frac{(2-\overline{\lambda })\overline{\lambda }}{128k} - \frac{(2-\overline{r})^3\overline{r}}{256k} \ge \frac{(2-(2\overline{r} - \frac{\overline{r}^2}{2}))(2\overline{r} - \frac{\overline{r}^2}{2})}{128k} - \frac{(2-\overline{r})^3\overline{r}}{256k} = \frac{(2-\overline{r})^2\overline{r}^2}{512k} \ge 0$. Thus, when $\frac{(2-\overline{r})^2}{32} < k$ and $\overline{r} < \frac{1}{2}$, the online retailer prefers the revenue-sharing contract to the fixed-fee contract and her profit is $\frac{(2-\overline{\lambda })\overline{\lambda }}{128k}$. When $\frac{(2-\overline{r})^2}{32} < k \le \frac{9}{128}$ and $\frac{1}{2} \le \overline{r}$, we have $\pi _r(\lambda ) - \pi _r(r) = \frac{(2-\overline{\lambda })\overline{\lambda }}{128k} - (\sqrt{2k}-4k) \ge \frac{(2-(2\overline{r} - \frac{\overline{r}^2}{2}))(2\overline{r} - \frac{\overline{r}^2}{2})}{128k} - (\sqrt{2k}-4k) \ge 0$. Thus, when $\frac{(2-\overline{r})^2}{32} < k \le \frac{9}{128}$ and $\frac{1}{2} \le \overline{r}$, the online retailer prefers the revenue-sharing contract to the fixed-fee contract and her profit is $\frac{(2-\overline{\lambda })\overline{\lambda }}{128k}$. When $\frac{9}{128} < k$ and $\frac{1}{2} \le \overline{r}$, we have $\pi _r(\lambda ) - \pi _r(r) = \frac{(2-\overline{\lambda })\overline{\lambda }}{128k} - \frac{27}{4096k} \ge 0$ because $\overline{\lambda } \ge 2\overline{r} - \frac{\overline{r}^2}{2} \ge \frac{7}{8}$. Thus, when $\frac{9}{128} < k$ and $\frac{1}{2} \le \overline{r}$, the online retailer prefers the revenue-sharing contract to the fixed-fee contract and her profit is $\frac{(2-\overline{\lambda })\overline{\lambda }}{128k}$.

Next we consider the case with $\overline{\lambda } < 2\overline{r} - \frac{\overline{r}^2}{2}$. When $k \le \frac{(2-\overline{r})^2}{32}$ and $2\overline{r} - \overline{r}^2\le \overline{\lambda }$, we have $\pi _r(\lambda ) - \pi _r(r) = \frac{\overline{\lambda }}{8} - \frac{2\overline{r}-\overline{r}^2}{8} \ge \frac{2\overline{r} - \overline{r}^2}{8} - \frac{2\overline{r}-\overline{r}^2}{8} =0$. Thus, when $k \le \frac{(2-\overline{r})^2}{32}$ and $2\overline{r} - \overline{r}^2\le \overline{\lambda }$, the online retailer prefers the revenue-sharing contract to the fixed-fee contract and her profit is $\frac{\overline{\lambda }}{8}$. When $k \le \frac{(2-\overline{r})^2}{32}$ and $\overline{\lambda } < 2\overline{r} - \overline{r}^2$, we have $\pi _r(\lambda ) - \pi _r(r) = \frac{\overline{\lambda }}{8} - \frac{2\overline{r}-\overline{r}^2}{8} < \frac{2\overline{r} - \overline{r}^2}{8} - \frac{2\overline{r}-\overline{r}^2}{8} = 0$. Thus, when $k \le \frac{(2-\overline{r})^2}{32}$ and $\overline{\lambda } < 2\overline{r} - \overline{r}^2$, the online retailer prefers the fixed-fee contract to the revenue-sharing contract and her profit is $\frac{2\overline{r}-\overline{r}^2}{8}$. When $\frac{(2-\overline{r})^2}{32} < k \le \frac{1}{8}-\frac{\overline{\lambda }}{16}$, $\overline{r} <\frac{1}{2}$, and $\frac{(2-\overline{r})^3\overline{r}}{32k} \le \overline{\lambda }$, we have $\pi _r(\lambda ) - \pi _r(r) = \frac{\overline{\lambda }}{8} - \frac{(2-\overline{r})^3\overline{r}}{256k} \ge \frac{1}{8}\frac{(2-\overline{r})^3\overline{r}}{32k} - \frac{(2-\overline{r})^3\overline{r}}{256k} = 0$. Thus, when $\frac{(2-\overline{r})^2}{32} < k \le \frac{1}{8}-\frac{\overline{\lambda }}{16}$, $\overline{r} <\frac{1}{2}$, and $\frac{(2-\overline{r})^3\overline{r}}{32k} \le \overline{\lambda }$, the online retailer prefers the revenue-sharing contract to the fixed-fee contract and her profit is $\frac{\overline{\lambda }}{8}$. When $\frac{(2-\overline{r})^2}{32} < k \le \frac{1}{8}-\frac{\overline{\lambda }}{16}$, $\overline{r} <\frac{1}{2}$, and $\overline{\lambda } < \frac{(2-\overline{r})^3\overline{r}}{32k}$, we have $\pi _r(\lambda ) - \pi _r(r) = \frac{\overline{\lambda }}{8} - \frac{(2-\overline{r})^3\overline{r}}{256k} < \frac{1}{8}\frac{(2-\overline{r})^3\overline{r}}{32k} - \frac{(2-\overline{r})^3\overline{r}}{256k} = 0$. Thus, when $\frac{(2-\overline{r})^2}{32} < k \le \frac{1}{8}-\frac{\overline{\lambda }}{16}$, $\overline{r} <\frac{1}{2}$, and $\overline{\lambda } < \frac{(2-\overline{r})^3\overline{r}}{32k}$, the online retailer prefers the fixed-fee contract to the revenue-sharing contract and her profit is $\frac{(2-\overline{r})^3\overline{r}}{256k}$. When $\frac{9+4\sqrt{2}}{256} \le k \le \frac{9}{128}$, $\frac{1}{2} \le \overline{r}$, and $8\sqrt{2k}-32k\le \overline{\lambda } \le \frac{7}{8}$, we have $\pi _r(\lambda ) - \pi _r(r) = \frac{\overline{\lambda }}{8} - (\sqrt{2k}-4k) \ge \frac{8\sqrt{2k}-32k}{8} - (\sqrt{2k}-4k) = 0$. Thus, when $\frac{9+4\sqrt{2}}{256} \le k \le \frac{9}{128}$, $\frac{1}{2} \le \overline{r}$, and $8\sqrt{2k}-32k\le \overline{\lambda } \le \frac{7}{8}$, the online retailer prefers the revenue-sharing contract to the fixed-fee contract and her profit is $\frac{\overline{\lambda }}{8}$. When $\frac{(2-\overline{r})^2}{32}< k <\frac{9+4\sqrt{2}}{256}$, $\frac{1}{2} \le \overline{r}$, and $\overline{\lambda } \le \frac{7}{8}$, we have $\pi _r(\lambda ) - \pi _r(r) = \frac{\overline{\lambda }}{8} - (\sqrt{2k}-4k) < 0$. Thus, when $\frac{(2-\overline{r})^2}{32}< k <\frac{9+4\sqrt{2}}{256}$, $\frac{1}{2} \le \overline{r}$, and $\overline{\lambda } \le \frac{7}{8}$, the online retailer prefers the fixed-fee contract to the revenue-sharing contract and her profit is $\sqrt{2k}-4k$. When $\frac{9+4\sqrt{2}}{256} \le k \le \frac{9}{128}$, $\frac{1}{2} \le \overline{r}$, and $\overline{\lambda } < 8\sqrt{2k}-32k$, we have $\pi _r(\lambda ) - \pi _r(r) = \frac{\overline{\lambda }}{8} - (\sqrt{2k}-4k) < \frac{8\sqrt{2k}-32k}{8} - (\sqrt{2k}-4k) = 0$. Thus, when $\frac{9+4\sqrt{2}}{256} \le k \le \frac{9}{128}$, $\frac{1}{2} \le \overline{r}$, and $\overline{\lambda } < 8\sqrt{2k}-32k$, the online retailer prefers the fixed-fee contract to the revenue-sharing contract and her profit is $\sqrt{2k}-4k$. When $\frac{9}{128} < k \le \frac{1}{8}-\frac{\overline{\lambda }}{16}$, $\frac{1}{2} \le \overline{r}$, and $\frac{27}{512k}\le \overline{\lambda } \le \frac{7}{8}$, we have $\pi _r(\lambda ) - \pi _r(r) = \frac{\overline{\lambda }}{8} - \frac{27}{4096k} \ge \frac{1}{8}\frac{27}{512k} - \frac{27}{4096k} = 0$. Thus, when $\frac{9}{128} < k \le \frac{1}{8}-\frac{\overline{\lambda }}{16}$, $\frac{1}{2} \le \overline{r}$, and $\frac{27}{512k}\le \overline{\lambda } \le \frac{7}{8}$, the online retailer prefers the revenue-sharing contract to the fixed-fee contract and her profit is $\frac{\overline{\lambda }}{8}$. When $\frac{9}{128} < k \le \frac{1}{8}-\frac{\overline{\lambda }}{16}$, $\frac{1}{2} \le \overline{r}$, and $\overline{\lambda } <\frac{27}{512k}$, we have $\pi _r(\lambda ) - \pi _r(r) = \frac{\overline{\lambda }}{8} - \frac{27}{4096k} < \frac{1}{8}\frac{27}{512k} - \frac{27}{4096k} = 0$. Thus, when $\frac{9}{128} < k \le \frac{1}{8}-\frac{\overline{\lambda }}{16}$, $\frac{1}{2} \le \overline{r}$, and $\overline{\lambda } <\frac{27}{512k}$, the online retailer prefers the fixed-fee contract to the revenue-sharing contract and her profit is $\frac{27}{4096k}$. When $\frac{9+4\sqrt{2}}{256} \le k \le \frac{1}{8}-\frac{\overline{\lambda }}{16}$, $\frac{1}{2} \le \overline{r}$, and $\frac{7}{8} < \overline{\lambda }$, we have $\pi _r(\lambda ) - \pi _r(r) = \frac{\overline{\lambda }}{8} - (\sqrt{2k}-4k) \ge 0$. Thus, when $\frac{9+4\sqrt{2}}{256} \le k \le \frac{1}{8}-\frac{\overline{\lambda }}{16}$, $\frac{1}{2} \le \overline{r}$, and $\frac{7}{8} < \overline{\lambda }$, the online retailer prefers the revenue-sharing contract to the fixed-fee contract and her profit is $\frac{\overline{\lambda }}{8}$. When $\frac{(2-\overline{r})^2}{32}< k < \frac{9+4\sqrt{2}}{256}$, $\frac{1}{2} \le \overline{r}$, and $8\sqrt{2k}-32k \le \overline{\lambda }$, we have $\pi _r(\lambda ) - \pi _r(r) = \frac{\overline{\lambda }}{8} - (\sqrt{2k}-4k) > \frac{8\sqrt{2k}-32k}{8} - (\sqrt{2k}-4k) = 0$. Thus, when $\frac{(2-\overline{r})^2}{32}< k < \frac{9+4\sqrt{2}}{256}$, $\frac{1}{2} \le \overline{r}$, and $8\sqrt{2k}-32k \le \overline{\lambda }$, the online retailer prefers the revenue-sharing contract to the fixed-fee contract and her profit is $\frac{\overline{\lambda }}{8}$. When $\frac{(2-\overline{r})^2}{32}< k < \frac{9+4\sqrt{2}}{256}$, $\frac{1}{2} \le \overline{r}$, and $\frac{7}{8}< \overline{\lambda } <8\sqrt{2k}-32k$, we have $\pi _r(\lambda ) - \pi _r(r) = \frac{\overline{\lambda }}{8} - (\sqrt{2k}-4k) < \frac{8\sqrt{2k}-32k}{8} - (\sqrt{2k}-4k) = 0$. Thus, when $\frac{(2-\overline{r})^2}{32}< k < \frac{9+4\sqrt{2}}{256}$, $\frac{1}{2} \le \overline{r}$, and $\frac{7}{8}< \overline{\lambda } <8\sqrt{2k}-32k$, the online retailer prefers the fixed-fee contract to the revenue-sharing contract and her profit is $\sqrt{2k}-4k$. When $\frac{1}{8}-\frac{\overline{\lambda }}{16} < k$, $\overline{r} <\frac{1}{2}$, and $\overline{\lambda } \le 1-\frac{\sqrt{2}\sqrt{2-8\overline{r}+12\overline{r}^2-6\overline{r}^3+\overline{r}^4}}{2}$, we have $\pi _r(\lambda ) - \pi _r(r) = \frac{(2-\overline{\lambda })\overline{\lambda }}{128k} - \frac{(2-\overline{r})^3\overline{r}}{256k} \le \frac{1}{128k}(1+\frac{\sqrt{2}\sqrt{2-8\overline{r}+12\overline{r}^2-6\overline{r}^3 +\overline{r}^4}}{2})(1-\frac{\sqrt{2}\sqrt{2-8\overline{r}+12\overline{r}^2-6\overline{r}^3+\overline{r}^4}}{2}) - \frac{(2-\overline{r})^3\overline{r}}{256k} = 0$. Thus, when $\frac{1}{8}-\frac{\overline{\lambda }}{16} < k$, $\overline{r} <\frac{1}{2}$, and $\overline{\lambda } \le 1-\frac{\sqrt{2}\sqrt{2-8\overline{r}+12\overline{r}^2-6\overline{r}^3+\overline{r}^4}}{2}$, the online retailer prefers the fixed-fee contract to the revenue-sharing contract and her profit is $\frac{(2-\overline{r})^3\overline{r}}{256k}$. When $\frac{1}{8}-\frac{\overline{\lambda }}{16} < k$, $\overline{r} <\frac{1}{2}$, and $1-\frac{\sqrt{2}\sqrt{2-8\overline{r}+12\overline{r}^2-6\overline{r}^3+\overline{r}^4}}{2} < \overline{\lambda }$, we have $\pi _r(\lambda ) - \pi _r(r) = \frac{(2-\overline{\lambda })\overline{\lambda }}{128k} - \frac{(2-\overline{r})^3\overline{r}}{256k} > \frac{1}{128k}(1+\frac{\sqrt{2}\sqrt{2-8\overline{r}+12\overline{r}^2-6\overline{r}^3 +\overline{r}^4}}{2})(1-\frac{\sqrt{2}\sqrt{2-8\overline{r}+12\overline{r}^2-6\overline{r}^3+\overline{r}^4}}{2}) - \frac{(2-\overline{r})^3\overline{r}}{256k} = 0$. Thus, when $\frac{1}{8}-\frac{\overline{\lambda }}{16} < k$, $\overline{r} <\frac{1}{2}$, and $1-\frac{\sqrt{2}\sqrt{2-8\overline{r}+12\overline{r}^2-6\overline{r}^3+\overline{r}^4}}{2} < \overline{\lambda }$, the online retailer prefers the revenue-sharing contract to the fixed-fee contract and her profit is $\frac{(2-\overline{\lambda })\overline{\lambda }}{128k}$. When $\frac{1}{8}-\frac{\overline{\lambda }}{16} < k$, $\frac{1}{2}\le \overline{r}$, and $\overline{\lambda } \le 1- \frac{\sqrt{10}}{8}$, we have $\pi _r(\lambda ) - \pi _r(r) = \frac{(2-\overline{\lambda })\overline{\lambda }}{128k} - \frac{27}{4096k} \le 0$. Thus, when $\frac{1}{8}-\frac{\overline{\lambda }}{16} < k$, $\frac{1}{2}\le \overline{r}$, and $\overline{\lambda } \le 1- \frac{\sqrt{10}}{8}$, the online retailer prefers the fixed-fee contract to the revenue-sharing contract and her profit is $\frac{27}{4096k}$. When $\frac{1}{8}-\frac{\overline{\lambda }}{16} < k$, $\frac{1}{2}\le \overline{r}$, and $1- \frac{\sqrt{10}}{8} < \overline{\lambda } \le \frac{7}{8}$, we have $\pi _r(\lambda ) - \pi _r(r) = \frac{(2-\overline{\lambda })\overline{\lambda }}{128k} - \frac{27}{4096k} > 0$. Thus, when $\frac{1}{8}-\frac{\overline{\lambda }}{16} < k$, $\frac{1}{2}\le \overline{r}$, and $1- \frac{\sqrt{10}}{8} < \overline{\lambda } \le \frac{7}{8}$, the online retailer prefers the revenue-sharing contract to the fixed-fee contract and her profit is $\frac{(2-\overline{\lambda })\overline{\lambda }}{128k}$. When $\frac{1}{8}-\frac{\overline{\lambda }}{16} < k \le \frac{9}{128}$, $\frac{1}{2}\le \overline{r}$, and $\frac{7}{8} < \overline{\lambda }$, we have $\pi _r(\lambda ) - \pi _r(r) = \frac{(2-\overline{\lambda })\overline{\lambda }}{128k} - (\sqrt{2k}-4k) \ge 0$ because $\frac{1}{16} < k \le \frac{9}{128}$. Thus, when $\frac{1}{8}-\frac{\overline{\lambda }}{16} < k \le \frac{9}{128}$, $\frac{1}{2}\le \overline{r}$, and $\frac{7}{8} < \overline{\lambda }$, the online retailer prefers the revenue-sharing contract to the fixed-fee contract and her profit is $\frac{(2-\overline{\lambda })\overline{\lambda }}{128k}$. When $\frac{9}{128}< k$, $\frac{1}{2}\le \overline{r}$, and $\frac{7}{8} < \overline{\lambda }$, we have $\pi _r(\lambda ) - \pi _r(r) = \frac{(2-\overline{\lambda })\overline{\lambda }}{128k} - \frac{27}{4096k} \ge 0$ because $\frac{(2-\overline{\lambda })\overline{\lambda }}{128k}$ is non-decreasing in $\overline{\lambda }$. Thus, when $\frac{9}{128}< k$, $\frac{1}{2}\le \overline{r}$, and $\frac{7}{8} < \overline{\lambda }$, the online retailer prefers the revenue-sharing contract to the fixed-fee contract and her profit is $\frac{(2-\overline{\lambda })\overline{\lambda }}{128k}$.

From the above cases, we have the results in Table 9, which explicitly reports the regions (each of which includes the profits of the online retailer under the two contracts and the difference between the two profits) and sheds more light on the interpretation of Table 4. Note that in the fourth column, “$+$” represents that $\pi _r(\lambda ) - \pi _r(r)\ge 0$, and “−” represents that $\pi _r(\lambda ) - \pi _r(r)<0$. This completes the proof of Proposition 1.

To investigate how the retailer’s contact choice affects the manufacturer’s profit, we compare the manufacturer’s profits when the online retailer chooses a revenue-sharing contract and when she chooses a fixed-fee contract as follows. From the results in Table 1, when $k \le \frac{1}{8}-\frac{\overline{\lambda }}{16}$, we have that the manufacturer’s profit is $\frac{2-8k-\overline{\lambda }}{8}$, and when $k > \frac{1}{8}-\frac{\overline{\lambda }}{16}$, we have that the manufacturer’s profit is $\frac{(2-\overline{\lambda })^2}{256k}$. From the results in Table 2, when $k\le \frac{(2-\overline{r})^2}{32}$, we have that the manufacturer’s profit is $\frac{4-16k-4\overline{r}+\overline{r}^2}{16}$, when $\frac{(2-\overline{r})^2}{32}<k$ and $\overline{r}< \frac{1}{2}$, we have that the manufacturer’s profit is $\frac{(2-\overline{r})^4}{1024k}$, when $\frac{(2-\overline{r})^2}{32}<k\le \frac{9}{128}$ and $\frac{1}{2}\le \overline{r}$, we have that the manufacturer’s profit is k, and when $\frac{9}{128}<k$ and $\frac{1}{2}\le \overline{r}$, we have that the manufacturer’s profit is $\frac{81}{16384k}$.

Next we compare the above-defined results to present the manufacturer’s profits under the revenue-sharing and fixed-fee contracts and show the manufacturer’s choice of contract. Let $\pi _m(\lambda )$ and $\pi _m(r)$ be the profits of the manufacturer under the revenue-sharing and fixed-fee contracts, respectively. We first consider the case with $2\overline{r} - \frac{\overline{r}^2}{2} \le \overline{\lambda }$. In this case, since $\overline{\lambda }\le 1$, we have $\overline{r}\le 2 - \sqrt{2}$. In this case, when $k\le \frac{1}{8}-\frac{\overline{\lambda }}{16}$, we have $\pi _m(\lambda ) - \pi _m(r) = \frac{2-8k-\overline{\lambda }}{8} - \frac{4-16k-4\overline{r}+\overline{r}^2}{16} = \frac{4\overline{r}-\overline{r}^2-2\overline{\lambda }}{16} \le \frac{1}{16}(4\overline{r}-\overline{r}^2-2(2\overline{r}-\frac{\overline{r}^2}{2})) = 0$. Thus, when $k\le \frac{1}{8}-\frac{\overline{\lambda }}{16}$, the manufacturer prefers the fixed-fee contract to the revenue-sharing contract and his profit is $\frac{4-16k-4\overline{r}+\overline{r}^2}{16}$. When $\frac{1}{8}-\frac{\overline{\lambda }}{16} < k \le \frac{(2-\overline{r})^2}{32}$, we have $2-\overline{\lambda }<16k$, which implies $\pi _m(\lambda ) - \pi _m(r) = \frac{(2-\overline{\lambda })^2}{256k} - \frac{4-16k-4\overline{r}+\overline{r}^2}{16} \le \frac{(16k)^2}{256k} - \frac{4-16k-4\overline{r}+\overline{r}^2}{16} =2k- \frac{(2-\overline{r})^2}{16} \le 2\frac{(2-\overline{r})^2}{32}- \frac{(2-\overline{r})^2}{16} = 0$. Thus, when $\frac{1}{8}-\frac{\overline{\lambda }}{16} < k \le \frac{(2-\overline{r})^2}{32}$, the manufacturer prefers the fixed-fee contract to the revenue-sharing contract and his profit is $\frac{4-16k-4\overline{r}+\overline{r}^2}{16}$. When $\frac{(2-\overline{r})^2}{32} < k$ and $\overline{r} < \frac{1}{2}$, we have $\pi _m(\lambda ) - \pi _m(r) = \frac{(2-\overline{\lambda })^2}{256k} - \frac{(2-\overline{r})^4}{1024k} \le \frac{(2-(2\overline{r} - \frac{\overline{r}^2}{2}))^2}{256k} - \frac{(2-\overline{r})^4}{1024k} = 0$. Thus, when $\frac{(2-\overline{r})^2}{32} < k$ and $\overline{r} < \frac{1}{2}$, the manufacturer prefers the fixed-fee contract to the revenue-sharing contract and his profit is $\frac{(2-\overline{r})^4}{1024k}$. When $\frac{(2-\overline{r})^2}{32} < k \le \frac{9}{128}$ and $\frac{1}{2} \le \overline{r}$, we have $\pi _m(\lambda ) - \pi _m(r) = \frac{(2-\overline{\lambda })^2}{256k} -k \le \frac{(2-(2-16k))^2}{256k} -k = 0$ since $2-16k\le 2-16\frac{(2-\overline{r})^2}{32}=2\overline{r} - \frac{\overline{r}^2}{2}\le \overline{\lambda }$. Thus, when $\frac{(2-\overline{r})^2}{32} < k \le \frac{9}{128}$ and $\frac{1}{2} \le \overline{r}$, the manufacturer prefers the fixed-fee contract to the revenue-sharing contract and his profit is k. When $\frac{9}{128} < k$ and $\frac{1}{2} \le \overline{r}$, we have $\pi _m(\lambda ) - \pi _m(r) = \frac{(2-\overline{\lambda })^2}{256k} - \frac{81}{16384k} \le \frac{(2-\frac{7}{8})^2}{256k} - \frac{81}{16384k} =0$ since $\overline{\lambda } \ge 2\overline{r} - \frac{\overline{r}^2}{2} \ge \frac{7}{8}$. Thus, when $\frac{9}{128} < k$ and $\frac{1}{2} \le \overline{r}$, the manufacturer prefers the fixed-fee contract to the revenue-sharing contract and his profit is $\frac{81}{16384k}$.

Next we consider the case with $\overline{\lambda } < 2\overline{r} - \frac{\overline{r}^2}{2}$. When $k \le \frac{(2-\overline{r})^2}{32}$ and $2\overline{r} - \overline{r}^2\le \overline{\lambda }$, we have $\pi _m(\lambda ) - \pi _m(r) = \frac{2-8k-\overline{\lambda }}{8} - \frac{4-16k-4\overline{r}+\overline{r}^2}{16} = \frac{4\overline{r}-\overline{r}^2-2\overline{\lambda }}{16} \ge \frac{1}{16}(4\overline{r}-\overline{r}^2-2(2\overline{r}-\frac{\overline{r}^2}{2})) = 0$. Thus, when $k \le \frac{(2-\overline{r})^2}{32}$ and $2\overline{r} - \overline{r}^2\le \overline{\lambda }$, the manufacturer prefers the revenue-sharing contract to the fixed-fee contract and his profit is $\frac{2-8k-\overline{\lambda }}{8}$. When $k \le \frac{(2-\overline{r})^2}{32}$ and $\overline{\lambda } < 2\overline{r} - \overline{r}^2$, we have $\pi _m(\lambda ) - \pi _m(r) = \frac{2-8k-\overline{\lambda }}{8} - \frac{4-16k-4\overline{r}+\overline{r}^2}{16} = \frac{4\overline{r}-\overline{r}^2-2\overline{\lambda }}{16} \ge \frac{1}{16}(4\overline{r}-\overline{r}^2-2(2\overline{r}-\overline{r}^2)) = \frac{\overline{r}^2}{16}\ge 0$. Thus, when $k \le \frac{(2-\overline{r})^2}{32}$ and $\overline{\lambda } < 2\overline{r} - \overline{r}^2$, the manufacturer prefers the revenue-sharing contract to the fixed-fee contract and his profit is $\frac{2-8k-\overline{\lambda }}{8}$. When $\frac{(2-\overline{r})^2}{32} < k \le \frac{1}{8}-\frac{\overline{\lambda }}{16}$, $\overline{r} <\frac{1}{2}$, and $\frac{(2-\overline{r})^3\overline{r}}{32k} \le \overline{\lambda } \le 2-8k-\frac{(2-\overline{r})^4}{128k}$, we have $\pi _m(\lambda ) - \pi _m(r) = \frac{2-8k-\overline{\lambda }}{8} - \frac{(2-\overline{r})^4}{1024k} \ge \frac{1}{8}(2-8k-(2-8k-\frac{(2-\overline{r})^4}{128k})) - \frac{(2-\overline{r})^4}{1024k} = 0$. Thus, when $\frac{(2-\overline{r})^2}{32} < k \le \frac{1}{8}-\frac{\overline{\lambda }}{16}$, $\overline{r} <\frac{1}{2}$, and $\frac{(2-\overline{r})^3\overline{r}}{32k} \le \overline{\lambda }\le 2-8k-\frac{(2-\overline{r})^4}{128k}$, the manufacturer prefers the revenue-sharing contract to the fixed-fee contract and his profit is $\frac{2-8k-\overline{\lambda }}{8}$. When $\frac{(2-\overline{r})^2}{32} < k \le \frac{1}{8}-\frac{\overline{\lambda }}{16}$, $\overline{r} <\frac{1}{2}$, and $2-8k-\frac{(2-\overline{r})^4}{128k} \le \overline{\lambda }$, we have $\pi _m(\lambda ) - \pi _m(r) = \frac{2-8k-\overline{\lambda }}{8} - \frac{(2-\overline{r})^4}{1024k} \le \frac{1}{8}(2-8k-(2-8k-\frac{(2-\overline{r})^4}{128k})) - \frac{(2-\overline{r})^4}{1024k} = 0$. Thus, when $\frac{(2-\overline{r})^2}{32} < k \le \frac{1}{8}-\frac{\overline{\lambda }}{16}$, $\overline{r} <\frac{1}{2}$, and $2-8k-\frac{(2-\overline{r})^4}{128k} \le \overline{\lambda }$, the manufacturer prefers the revenue-sharing contract to the fixed-fee contract and his profit is $\frac{(2-\overline{r})^4}{1024k}$. When $\frac{(2-\overline{r})^2}{32} < k \le \frac{1}{8}-\frac{\overline{\lambda }}{16}$, $\overline{r} <\frac{1}{2}$, and $\overline{\lambda } < \frac{(2-\overline{r})^3\overline{r}}{32k}$, we have $\overline{\lambda }\le 2-16k$. There are two cases to consider. In one case with $\frac{(2-\overline{r})^3\overline{r}}{32k} \le 2-16k$, implying that $k\le \frac{1}{16}+\sqrt{\frac{1}{256}-\frac{(2-\overline{r})^3\overline{r}}{512}}$, we have $\pi _m(\lambda ) - \pi _m(r) = \frac{2-8k-\overline{\lambda }}{8} - \frac{(2-\overline{r})^4}{1024k} \ge \frac{2-8k}{8}-\frac{1}{8}\frac{(2-\overline{r})^3\overline{r}}{32k} - \frac{(2-\overline{r})^4}{1024k} \ge \frac{1}{4}-\frac{(2-\overline{r})^2}{32}-\frac{1}{8}\frac{(2-\overline{r})^3\overline{r}}{32}\frac{1}{\frac{(2-\overline{r})^2}{32}} - \frac{(2-\overline{r})^4}{1024}\frac{1}{\frac{(2-\overline{r})^2}{32}} = \frac{\overline{r}^2}{16} \ge 0$. In the other case with $2-16k<\frac{(2-\overline{r})^3\overline{r}}{32k}$, implying $\overline{\lambda }\le 2-16k$ and $\frac{1}{16}+\sqrt{\frac{1}{256}-\frac{(2-\overline{r})^3\overline{r}}{512}}<k$, we have $\pi _m(\lambda ) - \pi _m(r) = \frac{2-8k-\overline{\lambda }}{8} - \frac{(2-\overline{r})^4}{1024k} \ge \frac{2-8k-(2-16k)}{8} - \frac{(2-\overline{r})^4}{1024k} \ge \frac{(2-\overline{r})^2}{32} - \frac{(2-\overline{r})^4}{1024}\frac{1}{\frac{(2-\overline{r})^2}{32}} =k \ge 0$. Thus, when $\frac{(2-\overline{r})^2}{32} < k \le \frac{1}{8}-\frac{\overline{\lambda }}{16}$, $\overline{r} <\frac{1}{2}$, and $\overline{\lambda } < \frac{(2-\overline{r})^3\overline{r}}{32k}$, the manufacturer prefers the revenue-sharing contract to the fixed-fee contract and his profit is $\frac{2-8k-\overline{\lambda }}{8}$. When $\frac{9+4\sqrt{2}}{256} \le k \le \frac{9}{128}$, $\frac{1}{2} \le \overline{r}$, and $8\sqrt{2k}-32k\le \overline{\lambda } \le \frac{7}{8}$, we have $\pi _m(\lambda ) - \pi _m(r) = \frac{2-8k-\overline{\lambda }}{8} -k =\frac{2-\overline{\lambda }}{8} -2k \ge \frac{2-\frac{7}{8}}{8} -2\frac{9}{128} = 0$. Thus, when $\frac{9+4\sqrt{2}}{256} \le k \le \frac{9}{128}$, $\frac{1}{2} \le \overline{r}$, and $8\sqrt{2k}-32k\le \overline{\lambda } \le \frac{7}{8}$, the manufacturer prefers the revenue-sharing contract to the fixed-fee contract and his profit is $\frac{2-8k-\overline{\lambda }}{8}$. When $\frac{(2-\overline{r})^2}{32}< k <\frac{9+4\sqrt{2}}{256}$, $\frac{1}{2} \le \overline{r}$, and $\overline{\lambda } \le \frac{7}{8}$, we have $\pi _m(\lambda ) - \pi _m(r) = \frac{2-8k-\overline{\lambda }}{8} -k =\frac{2-\overline{\lambda }}{8} -2k \ge \frac{2-\frac{7}{8}}{8} -2\frac{9+4\sqrt{2}}{256} > 0$. Thus, when $\frac{(2-\overline{r})^2}{32}< k <\frac{9+4\sqrt{2}}{256}$, $\frac{1}{2} \le \overline{r}$, and $\overline{\lambda } \le \frac{7}{8}$, the manufacturer prefers the revenue-sharing contract to the fixed-fee contract and his profit is $\frac{2-8k-\overline{\lambda }}{8}$. When $\frac{9+4\sqrt{2}}{256} \le k \le \frac{9}{128}$, $\frac{1}{2} \le \overline{r}$, and $\overline{\lambda } < 8\sqrt{2k}-32k$, we have $\pi _m(\lambda ) - \pi _m(r) = \frac{2-8k-\overline{\lambda }}{8} -k =\frac{2-\overline{\lambda }}{8} -2k \ge \frac{2-(2-16k)}{8} -2k = 0$ because $\overline{\lambda } < 8\sqrt{2k}-32k \le 2-16k$. Thus, when $\frac{9+4\sqrt{2}}{256} \le k \le \frac{9}{128}$, $\frac{1}{2} \le \overline{r}$, and $\overline{\lambda } < 8\sqrt{2k}-32k$, the manufacturer prefers the revenue-sharing contract to the fixed-fee contract and his profit is $\frac{2-8k-\overline{\lambda }}{8}$. When $\frac{9}{128} < k \le \frac{1}{8}-\frac{\overline{\lambda }}{16}$, $\frac{1}{2} \le \overline{r}$, and $\frac{27}{512k}\le \overline{\lambda } \le \frac{7}{8}$, we have $\pi _m(\lambda ) - \pi _m(r) = \frac{2-8k-\overline{\lambda }}{8} - \frac{81}{16384k} \ge \frac{16k-8k}{8} - \frac{81}{16384k} \ge \frac{9}{128} - \frac{81}{16384}\frac{1}{\frac{9}{128}} \ge 0$ because $k \le \frac{1}{8}-\frac{\overline{\lambda }}{16}$, implying $16k\le 2-\overline{\lambda }$. Thus, when $\frac{9}{128} < k \le \frac{1}{8}-\frac{\overline{\lambda }}{16}$, $\frac{1}{2} \le \overline{r}$, and $\frac{27}{512k}\le \overline{\lambda } \le \frac{7}{8}$, the manufacturer prefers the revenue-sharing contract to the fixed-fee contract and his profit is $\frac{2-8k-\overline{\lambda }}{8}$. When $\frac{9}{128} < k \le \frac{1}{8}-\frac{\overline{\lambda }}{16}$, $\frac{1}{2} \le \overline{r}$, and $\overline{\lambda } <\frac{27}{512k}$, we have $\pi _m(\lambda ) - \pi _m(r) = \frac{2-8k-\overline{\lambda }}{8} - \frac{81}{16384k} \ge \frac{16k-8k}{8} - \frac{81}{16384k} \ge \frac{9}{128} - \frac{81}{16384}\frac{1}{\frac{9}{128}} \ge 0$ because $k \le \frac{1}{8}-\frac{\overline{\lambda }}{16}$, implying $16k\le 2-\overline{\lambda }$. Thus, when $\frac{9}{128} < k \le \frac{1}{8}-\frac{\overline{\lambda }}{16}$, $\frac{1}{2} \le \overline{r}$, and $\overline{\lambda } <\frac{27}{512k}$, the manufacturer prefers the revenue-sharing contract to the fixed-fee contract and his profit is $\frac{2-8k-\overline{\lambda }}{8}$. When $\frac{9+4\sqrt{2}}{256} \le k \le \frac{1}{8}-\frac{\overline{\lambda }}{16}$, $\frac{1}{2} \le \overline{r}$, and $\frac{7}{8} < \overline{\lambda }$, we have $\pi _m(\lambda ) - \pi _m(r) = \frac{2-8k-\overline{\lambda }}{8} -k =\frac{2-\overline{\lambda }}{8} -2k \ge \frac{2-(2-16k)}{8} -2k =0$ because $k \le \frac{1}{8}-\frac{\overline{\lambda }}{16}$ implying $\overline{\lambda }\le 2-16k$. Thus, when $\frac{9+4\sqrt{2}}{256} \le k \le \frac{1}{8}-\frac{\overline{\lambda }}{16}$, $\frac{1}{2} \le \overline{r}$, and $\frac{7}{8} < \overline{\lambda }$, the manufacturer prefers the revenue-sharing contract to the fixed-fee contract and his profit is $\frac{2-8k-\overline{\lambda }}{8}$. When $\frac{(2-\overline{r})^2}{32}< k < \frac{9+4\sqrt{2}}{256}$, $\frac{1}{2} \le \overline{r}$, and $8\sqrt{2k}-32k \le \overline{\lambda }$, we have $\pi _m(\lambda ) - \pi _m(r) = \frac{2-8k-\overline{\lambda }}{8} -k =\frac{2-\overline{\lambda }}{8} -2k \ge \frac{2-(2-16k)}{8} -2k =0$ because $2-16k\ge 2-16\frac{(2-\overline{r})^2}{32} = 2\overline{r} - \frac{\overline{r}^2}{2} > \overline{\lambda }$. Thus, when $\frac{(2-\overline{r})^2}{32}< k < \frac{9+4\sqrt{2}}{256}$, $\frac{1}{2} \le \overline{r}$, and $8\sqrt{2k}-32k \le \overline{\lambda }$, the manufacturer prefers the revenue-sharing contract to the fixed-fee contract and his profit is $\frac{2-8k-\overline{\lambda }}{8}$. When $\frac{(2-\overline{r})^2}{32}< k < \frac{9+4\sqrt{2}}{256}$, $\frac{1}{2} \le \overline{r}$, and $\frac{7}{8}< \overline{\lambda } <8\sqrt{2k}-32k$, we have $\pi _m(\lambda ) - \pi _m(r) = \frac{2-8k-\overline{\lambda }}{8} -k =\frac{2-\overline{\lambda }}{8} -2k \ge \frac{2-(2-16k)}{8} -2k =0$ because $2-16k\ge 2-16\frac{(2-\overline{r})^2}{32} = 2\overline{r} - \frac{\overline{r}^2}{2} \ge 8\sqrt{2k}-32k > \overline{\lambda }$. Thus, when $\frac{(2-\overline{r})^2}{32}< k < \frac{9+4\sqrt{2}}{256}$, $\frac{1}{2} \le \overline{r}$, and $8\sqrt{2k}-32k \le \overline{\lambda }$, the manufacturer prefers the revenue-sharing contract to the fixed-fee contract and his profit is $\frac{2-8k-\overline{\lambda }}{8}$. When $\frac{1}{8}-\frac{\overline{\lambda }}{16} < k$, $\overline{r} <\frac{1}{2}$, and $\overline{\lambda } \le 1-\frac{\sqrt{2}\sqrt{2-8\overline{r}+12\overline{r}^2-6\overline{r}^3+\overline{r}^4}}{2}$, we have $\pi _m(\lambda ) - \pi _m(r) = \frac{(2-\overline{\lambda })^2}{256k} - \frac{(2-\overline{r})^4}{1024k} \ge \frac{1}{256k} (2-(1-\frac{\sqrt{2}\sqrt{2-8\overline{r}+12\overline{r}^2-6\overline{r}^3+\overline{r}^4}}{2}))^2 - \frac{(2-\overline{r})^4}{1024k} \ge 0$ since $0\le \overline{r} <\frac{1}{2}$. Thus, when $\frac{1}{8}-\frac{\overline{\lambda }}{16} < k$, $\overline{r} <\frac{1}{2}$, and $\overline{\lambda } \le 1-\frac{\sqrt{2}\sqrt{2-8\overline{r}+12\overline{r}^2-6\overline{r}^3+\overline{r}^4}}{2}$, the manufacturer prefers the revenue-sharing contract to the fixed-fee contract and his profit is $\frac{(2-\overline{\lambda })^2}{256k}$. When $\frac{1}{8}-\frac{\overline{\lambda }}{16} < k$, $\overline{r} <\frac{1}{2}$, and $1-\frac{\sqrt{2}\sqrt{2-8\overline{r}+12\overline{r}^2-6\overline{r}^3+\overline{r}^4}}{2} < \overline{\lambda }$, we have $\pi _m(\lambda ) - \pi _m(r) = \frac{(2-\overline{\lambda })^2}{256k} - \frac{(2-\overline{r})^4}{1024k} \ge \frac{1}{256k} (2-(2\overline{r} - \frac{\overline{r}^2}{2}))^2 - \frac{(2-\overline{r})^4}{1024k} = 0$. Thus, when $\frac{1}{8}-\frac{\overline{\lambda }}{16} < k$, $\overline{r} <\frac{1}{2}$, and $1-\frac{\sqrt{2}\sqrt{2-8\overline{r}+12\overline{r}^2-6\overline{r}^3+\overline{r}^4}}{2} < \overline{\lambda }$, the manufacturer prefers the revenue-sharing contract to the fixed-fee contract and his profit is $\frac{(2-\overline{\lambda })^2}{256k}$. When $\frac{1}{8}-\frac{\overline{\lambda }}{16} < k$, $\frac{1}{2}\le \overline{r}$, and $\overline{\lambda } \le \frac{7}{8}$, we have $\pi _m(\lambda ) - \pi _m(r) = \frac{(2-\overline{\lambda })^2}{256k} - \frac{81}{16384k} \ge \frac{(2-\frac{7}{8})^2}{256k} - \frac{81}{16384k} = 0$. Thus, when $\frac{1}{8}-\frac{\overline{\lambda }}{16} < k$, $\frac{1}{2}\le \overline{r}$, and $\overline{\lambda } \le \frac{7}{8}$, the manufacturer prefers the revenue-sharing contract to the fixed-fee contract and his profit is $\frac{(2-\overline{\lambda })^2}{256k}$. When $\frac{1}{8}-\frac{\overline{\lambda }}{16} < k \le \frac{9}{128}$, $\frac{1}{2}\le \overline{r}$, and $\frac{7}{8} < \overline{\lambda }$, we have $\pi _m(\lambda ) - \pi _m(r) = \frac{(2-\overline{\lambda })^2}{256k} - k \le \frac{(16k)^2}{256k} - k = 0$ since $\frac{1}{8}-\frac{\overline{\lambda }}{16} < k$, implying $2-\overline{\lambda }\le 16k$. Thus, when $\frac{1}{8}-\frac{\overline{\lambda }}{16} < k \le \frac{9}{128}$, $\frac{1}{2}\le \overline{r}$, and $\frac{7}{8} < \overline{\lambda }$, the manufacturer prefers the revenue-sharing contract to the fixed-fee contract and his profit is k. When $\frac{9}{128}< k$, $\frac{1}{2}\le \overline{r}$, and $\frac{7}{8} < \overline{\lambda }$, we have $\pi _m(\lambda ) - \pi _m(r) = \frac{(2-\overline{\lambda })^2}{256k} - \frac{81}{16384k} \le \frac{(2-\frac{7}{8})^2}{256k} - \frac{81}{16384k} = 0$. Thus, when $\frac{9}{128}< k$, $\frac{1}{2}\le \overline{r}$, and $\frac{7}{8} < \overline{\lambda }$, the manufacturer prefers the revenue-sharing contract to the fixed-fee contract and his profit is $\frac{81}{16384k}$.

Table 9 Profits under the two contracts and the difference between the two profits

1.4 Proof of Proposition 2

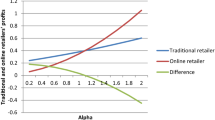
This proposition and Fig. 3 are obtained by conducting numerical simulation. Let $\overline{\lambda }=0.1$ and k vary from 0 to 0.2. Whereas the left graph of Fig. 3 has $\overline{r} =0.3$ and the right graph of Fig. 3 has $\overline{r} =0.6$. This completes the proof of Proposition 2.

1.5 Proof of Proposition 3

This proposition and Fig. 4 are obtained by conducting numerical simulation. Region I has $\overline{\lambda }=0.1$, $\overline{r}=0.04$, and $k\in [0,0.1]$. Region II has $\overline{\lambda }=0.1$, $\overline{r}=0.04$, and $k\in [0.2,0.3]$. Region III has $\overline{\lambda }=0.05$, $\overline{r}=0.04$, and $k\in [0,0.1]$. Region IV has $\overline{\lambda }=0.05$, $\overline{r}=0.04$, and $k\in [0.2,0.3]$. Region V has $\overline{\lambda }=0.1$, $\overline{r}=2/3$, and $k\in [5/8,2/3]$. Region VI has $\overline{\lambda }=0.1$, $\overline{r}=0.5$, and $k\in [0.2,0.3]$. This completes the proof of Proposition 3.

1.6 Analysis of Sect. 5.1: variation of the manufacturer’s cost of service function

1.7 Proof of Proposition 4

We derive the equilibrium results under the discrete service level case as follows. By using backward induction, we first consider the revenue-sharing contract. In the second stage, the manufacturer sets the price and service level. Given a revenue-sharing commission rate $\lambda$, when the manufacturer sets $s = s_h$, the manufacturer’s profit function is given by $\pi _{m}(p,s_h) = \frac{s_h(1-p)p(1-\lambda )}{2} + \frac{s_h(1-p)p}{2} - C$. From $\frac{\partial \pi _{m}(p,s_h)}{\partial p} = 0$, that is, $\frac{s_h(2p-1)p(\lambda - 2)}{2} = 0$, we have $p=\frac{1}{2}$. Thus, the optimal price is $p=\frac{1}{2}$, which then put back into the manufacturer’s profit function, gives $\pi _{m}(p,s_h) = \frac{s_h(2-\lambda )}{8} - C$. When the manufacturer sets $s = s_l$, the manufacturer’s profit function is given by $\pi _{m}(p,s_l) = \frac{s_l(1-p)p(1-\lambda )}{2} + \frac{s_l(1-p)p}{2}$. Similar to the above, one derives that the optimal retail price is $p=\frac{1}{2}$. As a result, the manufacturer’s profit is $\pi _{m}(p,s_l) = \frac{s_l(2-\lambda )}{8}$. Next, we consider the following cases.

• Case 1: If $\lambda \le 2- \frac{8C}{s_h - s_l}$, then the manufacturer will set $s = s_h$ and $p=\frac{1}{2}$, and hence his profit is $\pi _{m}(p,s_h) = \frac{s_h(2-\lambda )}{8} - C$.

• Case 2: If $\lambda > 2- \frac{8C}{s_h - s_l}$, then the manufacturer will set $s = s_l$ and $p=\frac{1}{2}$, and hence his profit is $\pi _{m}(p,s_l) = \frac{s_l(2-\lambda )}{8}$.

In the first stage, considering the manufacturer’s price and service level, the online retailer chooses a revenue-sharing commission rate $\lambda$ to maximize her profit. Because in the above two cases the manufacturer has the incentive to set $p=\frac{1}{2}$, we derive the online retailer’s profit function $\pi _r(\lambda ) = \frac{s\lambda }{8}$. When $\overline{\lambda }\le 2- \frac{8C}{s_h - s_l}$, which satisfies the condition of Case 1, the manufacturer will set $s = s_h$. Thus, we know that the online retailer’s profit function is maximized at $\lambda = \overline{\lambda }$, and therefore $\pi _r(\lambda ) = \frac{s_h\overline{\lambda }}{8}$. When $2- \frac{8C}{s_h - s_l}<0$, which satisfies the condition of Case 2, the manufacturer will set $s = s_l$. Thus, the online retailer’s profit function is still maximized at $\lambda = \overline{\lambda }$, and therefore $\pi _r(\lambda ) = \frac{s_l\overline{\lambda }}{8}$. When $0\le 2- \frac{8C}{s_h - s_l}< \overline{\lambda }$, which satisfies the conditions of Cases 1 and 2 simultaneously, based on the value of $\lambda$, the manufacturer is able to set $s = s_h$ or $s = s_l$. If $0\le 2- \frac{8C}{s_h - s_l}< \overline{\lambda }\le \frac{s_h}{s_l}(2- \frac{8C}{s_h - s_l})$, then the online retailer’s profit function is maximized at $\lambda = 2- \frac{8C}{s_h - s_l}$, and therefore $\pi _r(\lambda ) = \frac{s_h}{8}(2- \frac{8C}{s_h - s_l})$. If $\frac{s_h}{s_l}(2- \frac{8C}{s_h - s_l}) < \overline{\lambda }$, then the online retailer’s profit function is maximized at $\lambda = \overline{\lambda }$, and therefore $\pi _r(\lambda ) = \frac{s_l\overline{\lambda }}{8}$.

From the analysis above, we can obtain the following results as shown in Table 10.

Table 10 Equilibrium outcomes for the revenue-sharing contract under the discrete service level case

We next examine the equilibrium results under the fixed-fee contract. In the second stage, given a fixed rent r, the manufacturer sets the price and service level. When the manufacturer decides on $s = s_h$, the profit function is given by $\pi _{m}(p,s_h) = \frac{s_h(1-p)(p-r)}{2} + \frac{s_h(1-p)p}{2} - C$. Let $\frac{\partial \pi _{m}(p,s_h)}{\partial p} = 0$, that is, $\frac{s_h(2-4p+r)}{2} = 0$, which implies that $p=\frac{2+r}{4}$. Thus, it is optimal to set $p=\frac{2+r}{4}$, which in turn yields optimal $\pi _{m}(p,s_h) = \frac{s_h(2-r)^2}{16} - C$. When $s = s_l$, the manufacturer’s profit function is given by $\pi _{m}(p,s_l) = \frac{s_l(1-p)(p-r)}{2} + \frac{s_l(1-p)p}{2}$. Let $\frac{\partial \pi _{m}(p,s_l)}{\partial p} = 0$, that is, $\frac{s_l(2-4p+r)}{2} = 0$, which implies that $p=\frac{2+r}{4}$. Thus, it is optimal to set $p=\frac{2+r}{4}$, which in turn yields optimal $\pi _{m}(p,s_l) = \frac{s_l(2-r)^2}{16}$. Next, we consider the following cases.

• Case I: If $r \le 2- \sqrt{\frac{16C}{s_h - s_l}}$, then the manufacturer will set $s = s_h$ and $p=\frac{2+r}{4}$, and hence his profit is $\pi _{m}(p,s_h) = \frac{s_h(2-r)^2}{16} - C$.

• Case II: If $r > 2- \sqrt{\frac{16C}{s_h - s_l}}$, then the manufacturer will set $s = s_l$ and $p=\frac{2+r}{4}$, and hence his profit is $\pi _{m}(p,s_l) = \frac{s_l(2-r)^2}{16}$.

In the first stage, considering the manufacturer’s price and service level, the online retailer chooses a fixed rent r to maximize her profit. Because in the above two cases the manufacturer has the incentive to set $p=\frac{2+r}{4}$, we obtain the online retailer’s profit function $\pi _r(r) = \frac{s(2-r)r}{8}$. When $\overline{r}\le 2- \sqrt{\frac{16C}{s_h - s_l}}$, which satisfies the condition of Case I, the manufacturer will set $s = s_h$. Thus, the online retailer’s profit function is maximized at $r = \overline{r}$, and therefore $\pi _r(r) = \frac{s_h(2-\overline{r})\overline{r}}{8}$. When $2- \sqrt{\frac{16C}{s_h - s_l}} < 0$, which satisfies the condition of Case II, the manufacturer will set $s = s_l$. Thus, the online retailer’s profit function is maximized at $r = \overline{r}$, and therefore $\pi _r(r) = \frac{s_l(2-\overline{r})\overline{r}}{8}$. When $0\le 2- \sqrt{\frac{16C}{s_h - s_l}}< \overline{r}$, which satisfies the condition of Cases I and II simultaneously, the manufacturer will set $s = s_h$ or $s = s_l$. If $0\le 2- \sqrt{\frac{16C}{s_h - s_l}}< \overline{r} \le 1 - \sqrt{1-\frac{s_h}{s_l}\sqrt{\frac{16C}{s_h - s_l}}(2- \sqrt{\frac{16C}{s_h - s_l}})}$, then the online retailer’s profit function is maximized at $r = 2- \sqrt{\frac{16C}{s_h - s_l}}$, and therefore $\pi _r(r) = \frac{s_h}{8}\sqrt{\frac{16C}{s_h - s_l}}(2- \sqrt{\frac{16C}{s_h - s_l}})$. If $1 - \sqrt{1-\frac{s_h}{s_l}\sqrt{\frac{16C}{s_h - s_l}}(2- \sqrt{\frac{16C}{s_h - s_l}})} < \overline{r}$, then the online retailer’s profit function is maximized at $r = \overline{r}$, and therefore $\pi _r(r) = \frac{s_l(2-\overline{r})\overline{r}}{8}$.

From the above analysis, we obtain the results as shown in Table 11.

Table 11 Equilibrium outcomes for the fixed-fee contract under the discrete service level case

The parameter values used for drawing Fig. 5 basically follow (Kuksov and Liao, 2018) with the following values: $s_h = 1$ and $s_l = 0.4$. We also set $C = 0.1425$ and $\overline{r} = 0.05$ in Fig. 5a, and $C = 0.135375$ and $\overline{\lambda } = 0.1$ in Fig. 5b to make sure that we have a reasonable profit for the online retailer. This completes the proof of Proposition 4.

1.8 Analysis of Sect. 5.2.1: consumer channel preference

1.9 Proof of Corollary 1

When the manufacturer sets the same price in both channels, we derive the equilibrium results as follows. We first consider the revenue-sharing contract. Here, we need to consider two cases: $2p \ge 2 - t$ and $2p < 2 - t$.

Case I: $2p \ge 2 - t$. Using the first-order condition, $\frac{\partial \pi _{m}(p,s)}{\partial p} = 0$, we can derive $p=\frac{1}{3}$ or $p=1$. To make a profit, the manufacturer chooses to set $p=\frac{1}{3}$. From $\frac{\partial \pi _{m}(p,s)}{\partial s} = 0$, we have $s=\frac{(1 - p)^2p(2 -\lambda )}{4kt}$. Substituting the equilibrium price $p=\frac{1}{3}$ into $s=\frac{(1 - p)^2p(2 -\lambda )}{4kt}$, we can derive $s=\frac{2 -\lambda }{27kt}$. Next, we show that the manufacturer’s expected profit is maximized at $p=\frac{1}{3}$ and $s=\min \Big \{1, \frac{2 -\lambda }{27kt}\Big \}$ when $t\ge \frac{4}{3}$.

When $p=\frac{1}{3}$ and $s=\frac{2 -\lambda }{27kt} < 1$, the Hessian Matrix of the manufacturer’s profit function

$$\begin{aligned} \left[ \begin{array}{cc} \frac{\partial ^2 \pi _{m}(p,s)}{\partial p^2} &{} \frac{\partial ^2 \pi _{m}(p,s)}{\partial p \partial s}\\ \frac{\partial ^2 \pi _{m}(p,s)}{\partial s \partial p} &{} \frac{\partial ^2 \pi _{m}(p,s)}{\partial s^2} \end{array} \right] = \left[ \begin{array}{cc} \frac{s(\lambda -2)(4-6p)}{2t} &{} \frac{(3p-1)(1-p)(\lambda - 2)}{2t}\\ \frac{(3p-1)(1-p)(\lambda - 2)}{2t} &{} -2k \end{array} \right] = \left[ \begin{array}{cc} \frac{s(\lambda -2)}{t} &{} 0\\ 0 &{} -2k \end{array} \right] , \end{aligned}$$

is negative definite. This implies that the maximum expected profit is achieved at this point.

When $\frac{2 -\lambda }{27kt} \ge 1$, the first-order derivative of the manufacturer’s profit function with respect to s, $\frac{2(2 - \lambda )}{27t} - 2k s$, is positive for any $0\le s \le 1$, meaning that it is optimal to set $s = 1$.

Thus, when $t\ge \frac{4}{3}$, the equilibrium is $p=\frac{1}{3}$ and $s=\min \Big \{1, \frac{2 -\lambda }{27kt}\Big \}$.

Case II: $2p < 2 - t$. Using the first-order condition, $\frac{\partial \pi _{m}(p,s)}{\partial p} = 0$, we derive $p=\frac{4-t}{8}$. From $\frac{\partial \pi _{m}(p,s)}{\partial s} = 0$, we have $s=\frac{p(4-4p-t)(2 - \lambda )}{16k}$. Substituting the equilibrium price $p=\frac{4-t}{8}$ into $s=\frac{p(4-4p-t)(2 - \lambda )}{16k}$, we can derive $s=\frac{(4-t)^2(2 -\lambda )}{256k}$. Next, we show that the manufacturer’s expected profit is maximized at $p=\frac{4-t}{8}$ and $s=\min \Big \{1, \frac{(4-t)^2(2 -\lambda )}{256k}\Big \}$ when $t<\frac{4}{3}$.

When $p=\frac{4-t}{8}$ and $s= \frac{(4-t)^2(2 -\lambda )}{256k} < 1$, the Hessian Matrix of the manufacturer’s profit function

$$\begin{aligned} \left[ \begin{array}{cc} \frac{\partial ^2 \pi _{m}(p,s)}{\partial p^2} &{} \frac{\partial ^2 \pi _{m}(p,s)}{\partial p \partial s}\\ \frac{\partial ^2 \pi _{m}(p,s)}{\partial s \partial p} &{} \frac{\partial ^2 \pi _{m}(p,s)}{\partial s^2} \end{array} \right] = \left[ \begin{array}{cc} s(\lambda -2) &{} \frac{(-4+8p+t)(-2+\lambda )}{8}\\ \frac{(-4+8p+t)(-2+\lambda )}{8} &{} -2k \end{array} \right] = \left[ \begin{array}{cc} s(\lambda -2) &{} 0\\ 0 &{} -2k \end{array} \right] , \end{aligned}$$

is negative definite. This implies that the maximum expected profit is achieved at this point.

When $\frac{(4-t)^2(2 -\lambda )}{256k} \ge 1$, the first-order derivative of the manufacturer’s profit function with respect to s, $\frac{(4-t)^2(2 - \lambda )}{128} - 2k s$, is positive for any $0\le s \le 1$, meaning that it is optimal to set $s = 1$.

Thus, when $t < \frac{4}{3}$, the equilibrium is $p=\frac{4-t}{8}$ and $s=\min \Big \{1, \frac{(4-t)^2(2 -\lambda )}{256k}\Big \}$.

Considering the manufacturer’s price and service level, the online retailer chooses a revenue-sharing rate $\lambda$ to maximize her profit, $\pi _r(\lambda ) =p\lambda D_{\text {online}}$. We consider the following cases.

• Case 1: $t\ge \frac{4}{3}$ and $\frac{2 -\lambda }{27kt}\ge 1$. In this case, we have $\lambda \le 2-27kt$, the manufacturer sets $p=\frac{1}{3}$ and $s=1$, and the online retailer’s profit function becomes $\pi _r(\lambda ) = \frac{2\lambda }{27t}$. Thus, when $2-27kt\ge 0$, that is, $k\le \frac{2}{27t}$, the online retailer’s optimal decision is to set the revenue-sharing rate at $\lambda = \min \{\overline{\lambda },2-27kt\}$, and we derive the online retailer’s profit $\pi _r(\lambda ) = \frac{2\lambda }{27t}$.

• Case 2: $t\ge \frac{4}{3}$ and $\frac{2 -\lambda }{27kt} < 1$. In this case, we have $\lambda > 2-27kt$, the manufacturer sets $p=\frac{1}{3}$ and $s=\frac{2 -\lambda }{27kt}$, and the online retailer’s profit function becomes $\pi _r(\lambda ) = \frac{2\lambda (2-\lambda )}{27^2 k t^2}$. Thus, when $2-27kt < \overline{\lambda }$, that is, $k > \frac{2-\overline{\lambda }}{27t}$, the online retailer’s optimal decision is to set the revenue-sharing rate at $\lambda = \overline{\lambda }$, and we derive the online retailer’s profit $\pi _r(\lambda ) = \frac{2\overline{\lambda }(2-\overline{\lambda })}{729 k t^2}$.

• Case 3: $t < \frac{4}{3}$ and $\frac{(4-t)^2(2 -\lambda )}{256k} \ge 1$. In this case, we have $\lambda \le 2 - \frac{256k}{(4-t)^2}$, the manufacturer sets $p=\frac{4-t}{8}$ and $s = 1$, and the online retailer’s profit function becomes $\pi _r(\lambda ) = \frac{(4-t)^2\lambda }{128}$. Thus, when $0\le 2 - \frac{256k}{(4-t)^2}$, that is, $k \le \frac{(4-t)^2}{128}$, the online retailer’s optimal decision is to set the revenue-sharing rate at $\lambda = \min \Big \{\overline{\lambda }, 2 - \frac{256k}{(4-t)^2}\Big \}$, and we derive the online retailer’s profit $\pi _r(\lambda ) = \frac{(4-t)^2\lambda }{128}$.

• Case 4: $t < \frac{4}{3}$ and $\frac{(4-t)^2(2 -\lambda )}{256k} < 1$. In this case, we have $\lambda > 2 - \frac{256k}{(4-t)^2}$, the manufacturer sets $p=\frac{4-t}{8}$ and $s = \frac{(4-t)^2(2 -\lambda )}{256k}$, and the online retailer’s profit function becomes $\pi _r(\lambda ) = \frac{(4-t)^4(2 -\lambda )\lambda }{32768k}$. Thus, when $2 - \frac{256k}{(4-t)^2} < \overline{\lambda }$, that is, $k > \frac{(2-\overline{\lambda })(4-t)^2}{256}$, the online retailer’s optimal decision is to set the revenue-sharing rate at $\lambda = \overline{\lambda }$, and we derive the online retailer’s profit $\pi _r(\lambda ) = \frac{(4-t)^4(2-\overline{\lambda })\overline{\lambda }}{32768k}$.

Note that it is analytically difficult to compare the above four cases. Thus, to maintain the tractability of our analysis, let $\overline{\lambda }=0.1$. The results are presented in Table 12.

Table 12 Equilibrium outcomes for the revenue-sharing contract under the consumer channel preference case

Next, we derive the equilibrium results under the fixed-fee contract. We need to consider the following two cases: $2p \ge 2 - t$ and $2p < 2 - t$.

Case I: $2p \ge 2 - t$. Using the first-order condition, $\frac{\partial \pi _{m}(p,s)}{\partial p} = 0$, that is, $\frac{s(3p-1-r)(p-1)}{t} = 0$, we have $p=\frac{1+r}{3}$ or $p=1$. To make a profit, the manufacturer chooses to set $p=\frac{1+r}{3}$. From $\frac{\partial \pi _{m}(p,s)}{\partial s} = 0$, that is, $\frac{(1-p)^2 (p-r)}{2t} +\frac{(1-p)^2 p}{2t} - 2k s = 0$, we have $s=\frac{(1 - p)^2 (2p -r)}{4kt}$. Substituting the equilibrium price $p=\frac{1+r}{3}$ into $s=\frac{(1 - p)^2 (2p -r)}{4kt}$, we can derive $s= \frac{(2 -r)^3}{108kt}$. Next, we show that the manufacturer’s expected profit is maximized at $p=\frac{1+r}{3}$ and $s=\min \Big \{1, \frac{(2 -r)^3}{108kt}\Big \}$ when $t\ge \frac{4-2r}{3}$.

When $p=\frac{1+r}{3}$ and $s=\frac{(2 -r)^3}{108kt} < 1$, the Hessian Matrix of the manufacturer’s profit function

$$\begin{aligned} \left[ \begin{array}{cc} \frac{\partial ^2 \pi _{m}(p,s)}{\partial p^2} &{} \frac{\partial ^2 \pi _{m}(p,s)}{\partial p \partial s}\\ \frac{\partial ^2 \pi _{m}(p,s)}{\partial s \partial p} &{} \frac{\partial ^2 \pi _{m}(p,s)}{\partial s^2} \end{array} \right] = \left[ \begin{array}{cc} \frac{s(6p-4-r)}{t} &{} \frac{(3p-1-r)(p-1)}{t}\\ \frac{(3p-1-r)(p-1)}{t} &{} -2k \end{array} \right] = \left[ \begin{array}{cc} \frac{s(r-2)}{t} &{} 0\\ 0 &{} -2k \end{array} \right] , \end{aligned}$$

is negative definite. This implies that the maximum expected profit is achieved at this point.

When $\frac{(2 -r)^3}{108kt} \ge 1$, the first-order derivative of the manufacturer’s profit function with respect to s, $\frac{(1-p)^2 (p-r)}{2t} +\frac{(1-p)^2 p}{2t} - 2k s$, is positive for any $0\le s \le 1$, meaning that it is optimal to set $s = 1$.

Thus, when $t\ge \frac{4-2r}{3}$, the equilibrium is $p=\frac{1+r}{3}$ and $s=\min \Big \{1, \frac{(2 -r)^3}{108kt}\Big \}$.

Case II: $2p < 2 - t$. In this case, the first-order condition of the manufacturer’s objective function with respect to p is $\frac{\partial \pi _{m}(p,s)}{\partial p} = 0$, that is, $\frac{s(4-8p-t+2r)}{4} = 0$. Thus, we derive $p=\frac{4-t+2r}{8}$. The first-order condition with respect to s is $\frac{\partial \pi _{m}(p,s)}{\partial s} = 0$. Putting $p=\frac{4-t+2r}{8}$ into this equation we have $s= \frac{(2r+t-4)^2}{128k}$. Next, we show that the manufacturer’s expected profit is maximized at $p=\frac{4-t+2r}{8}$ and $s=\min \Big \{1, \frac{(2r+t-4)^2}{128k}\Big \}$ when $t< \frac{4-2r}{3}$.

When $p=\frac{4-t+2r}{8}$ and $s= \frac{(2r+t-4)^2}{128k} < 1$, the Hessian Matrix of the manufacturer’s profit function

$$\begin{aligned} \left[ \begin{array}{cc} \frac{\partial ^2 \pi _{m}(p,s)}{\partial p^2} &{} \frac{\partial ^2 \pi _{m}(p,s)}{\partial p\partial s}\\ \frac{\partial ^2 \pi _{m}(p,s)}{\partial s \partial p} &{} \frac{\partial ^2 \pi _{m}(p,s)}{\partial s^2} \end{array} \right] = \left[ \begin{array}{cc} -2s &{} \frac{(4-8p+2r-t)}{4}\\ \frac{(4-8p+2r-t)}{4} &{} -2k \end{array} \right] = \left[ \begin{array}{cc} -2s &{} 0\\ 0 &{} -2k \end{array} \right] , \end{aligned}$$

is negative definite. This implies that the maximum expected profit is achieved at this point.

When $\frac{(2r+t-4)^2}{128k} \ge 1$, the first-order derivative of the manufacturer’s profit function with respect to s, $\frac{(4-4p-t)(2p - r)}{8} - 2k s$, is positive for any $0\le s \le 1$, meaning that it is optimal to set $s = 1$.

Thus, when $t < \frac{4-2r}{3}$, the equilibrium is $p=\frac{4-t+2r}{8}$ and $s=\min \Big \{1, \frac{(2r+t-4)^2}{128k}\Big \}$.

Considering the manufacturer’s price and service level, the online retailer chooses a fixed rent r to maximize her profit, $\pi _r(r) =rD_{\text {online}}$. We need to consider the following cases.

Case 1: $t\ge \frac{4-2r}{3}$ and $\frac{(2 -r)^3}{108kt}\ge 1$. In this case, we have that $\frac{4-3t}{2} \le r \le 2-\root 3 \of {108kt}$, the manufacturer sets $p=\frac{1+r}{3}$ and $s=1$, and the online retailer’s profit function becomes $\pi _r(r) = \frac{(2-r)^2r}{18t}$. Thus, we have that (i) when $t\ge \frac{3.8}{3}$ and $k \le \frac{6.859}{108t}$, the online retailer’s optimal decision is to set the fixed rent at $r = \overline{r}$ and then the online retailer’s profit is $\pi _r(r) = \frac{0.361}{18t}$; (ii) when ($\frac{3.8}{3} \le t< \frac{4}{3}$ and $\frac{6.859}{108t} <k \le \frac{t^2}{32}$) or ($\frac{4}{3} \le t$ and $\frac{6.859}{108 t} <k \le \frac{2}{27t}$), the online retailer’s optimal decision is to set the fixed rent at $r = 2-\root 3 \of {108kt}$ and then the online retailer’s profit is $\pi _r(r) = 2k(\root 3 \of {\frac{2}{kt}}-3)$.

Case 2: $t\ge \frac{4-2r}{3}$ and $\frac{(2 -r)^3}{108kt}< 1$. In this case, we have that $r \ge 2-\frac{3t}{2}$ and $r > 2-\root 3 \of {108kt}$, the manufacturer sets $p=\frac{1+r}{3}$ and $s=\frac{(2 -r)^3}{108kt}$, and the online retailer’s profit function becomes $\pi _r(r) = \frac{(2-r)^5 r}{1944 k t^2}$. Thus, we have that when $t\ge \frac{3.8}{3}$ and $\frac{6.859}{108t} < k$, the online retailer’s optimal decision is to set the fixed rent at $r = \overline{r}$ and then the online retailer’s profit is $\pi _r(r) = \frac{2.4761}{1944kt^2}$.

Case 3: $t < \frac{4-2r}{3}$ and $\frac{(2r+t-4)^2}{128k} \ge 1$. In this case, because $2r+t-4 \le 0$, we have that $r\le \frac{4-t-\sqrt{128k}}{2}$ and $r < 2 - \frac{3t}{2}$. The manufacturer sets $p=\frac{4-t+2r}{8}$ and $s = 1$, and hence the online retailer’s profit function becomes $\pi _r(r) = \frac{(4-t-2r)r}{16}$. Because $0\le p=\frac{4-t+2r}{8} \le 1$, we have that $r \ge \frac{t-4}{2}$. Thus, we have that (i) when $\frac{3.8}{3}\le t < \frac{4}{3}$ and $k \le \frac{t^2}{32}$, the online retailer’s optimal decision is to set the fixed rent at $r = 2-\frac{3t}{2}$ and then the online retailer’s profit is $\pi _r(r) = \frac{t(4-3t)}{16}$; (ii) when ($t < \frac{3.8}{3}$ and $k \le \frac{t^2}{32}$) or ($t < \frac{4}{3}$ and $k < \frac{(3.8-t)^2}{128}$), the online retailer’s optimal decision is to set the fixed rent at $r = 0.1$ and then the online retailer’s profit is $\pi _r(r) = \frac{0.1(3.8-t)}{16}$; and (iii) when ($\frac{3.8}{3} \le t < \frac{4}{3}$ and $\frac{t^2}{32} < k \le \frac{(4-t)^2}{128}$) or ($0\le t <\frac{3.8}{3}$ and $\frac{(3.8-t)^2}{128}\le k \le \frac{(4-t)^2}{128}$), the online retailer’s optimal decision is to set the fixed rent at $r = \frac{4-t-\sqrt{128k}}{2}$ and then the online retailer’s profit is $\pi _r(r) = \frac{\sqrt{k}(4-8\sqrt{2k}-t)}{2\sqrt{2}}$.

Case 4: $t < \frac{4-2r}{3}$ and $\frac{(2r+t-4)^2}{128k} < 1$. In this case, we have that $\frac{4-t-\sqrt{128k}}{2}<r < 2 - \frac{3t}{2}$, the manufacturer sets $p=\frac{4-t+2r}{8}$ and $s = \frac{(2r+t-4)^2}{128k}$, and the online retailer’s profit function becomes $\pi _r(\lambda ) = \frac{(4-t-2r)^3r}{2048k}$. Thus, we have that (i) when $\frac{3.8}{3}\le t < \frac{4}{3}$ and $\frac{t^2}{32} < k$, the online retailer’s optimal decision is to set the fixed rent at $r = 2-\frac{3t}{2}$ and then the online retailer’s profit is $\pi _r(r) = \frac{t^3(4-3t)}{512k}$; and (ii) when $0\le t < \frac{3.8}{3}$ and $\frac{(3.8-t)^2}{128} < k$, the online retailer’s optimal decision is to set the fixed rent at $r = 0.1$ and then the online retailer’s profit is $\pi _r(r) = \frac{0.1(3.8-t)^3}{2048k}$.

Because it is analytically difficult to compare the four cases above, let $\overline{r}=0.1$. The results are presented in Table 13.

Table 13 Equilibrium results for the fixed-fee contract under the consumer channel preference case

Because solving analytically for the equilibrium outcomes in the case where the prices are equal is challenging and the analysis becomes quite complex when considering that the manufacturer sets different prices in both channels, we compute the equilibrium outcome for the online retailer numerically. We vary the unit misfit cost t from 0.5 to 1.5. Figure 6a, b depict the curves of $\pi _r$ and s under the two contracts, respectively.

We use the following example to illustrate how the main result is obtained in this model variation:

Let $\overline{\lambda } = 0.1$, $\overline{r} = 0.04$, and $k=\frac{1}{20}$. Then, when $t = 0.5$, under the revenue-sharing contract, $\pi _r(\lambda ) = 0.009288$ and $\pi _{m}(p,s) = 0.131976$; whereas under the fixed-fee contract, $\pi _r(r) = 0.007943$ and $\pi _{m}(p,s) = 0.133108$. Thus, the online retailer should adopt the revenue-sharing contract to maximize her profit. When $t = 1.3$, under the revenue-sharing contract, $\pi _r(\lambda ) = 0.005695$ and $\pi _{m}(p,s) = 0.058205$; whereas under the fixed-fee contract, $\pi _r(r) = 0.006301$ and $\pi _{m}(p,s) = 0.057382$. Thus, the online retailer should adopt the fixed-fee contract to maximize her profit. This completes the proof of Corollary 1.

1.10 Analysis of Sect. 5.2.2: lower consumer valuation of online purchasing

1.11 Proof of Corollary 2

Assuming that $p_1<1$ and $p_2<1$ and using the fact that V is uniformly distributed over [0,1], we can write the demands for the BM store and platform, $D_{\text {BM}}$ and $D_{\text {online}}$, as follows:

$$\begin{aligned} D_{\text {BM}}=\left\{ \begin{array}{ll} 0, &{}\hbox { if } \frac{p_1-p_2}{1-\theta }\ge 1,\\ s(1-\frac{p_1-p_2}{1-\theta }), &{}\hbox { if } \frac{p_2}{\theta }\le \frac{p_1-p_2}{1-\theta }<1,\\ s(1-p_1), &{}\hbox { if } \frac{p_1-p_2}{1-\theta }< \frac{p_2}{\theta }, \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} D_{\text {online}}=\left\{ \begin{array}{ll} s(1-\frac{p_2}{\theta }), &{}\hbox { if } \frac{p_1-p_2}{1-\theta }\ge 1,\\ s(\frac{p_1-p_2}{1-\theta }-\frac{p_2}{\theta }), &{}\hbox { if } \frac{p_2}{\theta }\le \frac{p_1-p_2}{1-\theta }<1,\\ 0, &{}\hbox { if } \frac{p_1-p_2}{1-\theta }< \frac{p_2}{\theta }. \end{array} \right. \end{aligned}$$

Observing the demand functions, we find that when $\frac{p_1-p_2}{1-\theta }\ge 1$, no consumer intends to buy offline, and when $\frac{p_1-p_2}{1-\theta }< \frac{p_2}{\theta }$, no consumer intends to buy online. Therefore, the manufacturer who implements a dual-channel distribution system, determines the retail prices $p_1$ and $p_2$ such that $\frac{p_2}{\theta }\le \frac{p_1-p_2}{1-\theta }<1$.

We further investigate parameter $\theta$’s effect on the online retailer’s profits and the two channels’ prices under the two contracts. Because the problem is analytically intractable, we study it numerically. We fix $k=\frac{1}{40}$, $\overline{\lambda } = 0.1$, and $\overline{r} = 0.04$ and vary the parameter $\theta$ from 0.1 to 0.9. Figure 7a, b depict the curves of $\pi _r$ and prices under the two contracts, respectively. This completes the proof of Corollary 2.

1.12 Analysis of Sect. 5.3: online returns and offline shopping costs

1.13 Proof of Corollary 3

When intra-SR is possible and the service level of the BM store is $s=1$, under the revenue-sharing contract, the manufacturer’s and online retailer’s profit functions are:

$$\begin{aligned} \pi _{m}(p_1,p_2)= & {} p_1D_{\text {BM}}+p_2(1-\lambda )(D_{\text {s-online}}+D_{\text {d-online}})-uD_{\text {d-online}} - C\\&\text { and } \pi _r(\lambda ) = p_2\lambda (D_{\text {s-online}}+D_{\text {d-online}}), \end{aligned}$$

where $D_{\text {s-online}}$ denotes the demands of consumers who have visited the BM store but eventually purchase online, $D_{\text {d-online}}$ denotes the demands of consumers who purchase online directly without visiting the BM store, and u is the unit cost of providing online return service. Table 14 summarizes the results of $D_{\text {BM}}$, $D_{\text {s-online}}$ and $D_{\text {d-online}}$ under different conditions and $\hat{p}$ is the expected offline price. In this case, we consider the demands that satisfy $D_{\text {BM}}>0$ and $D_{\text {s-online}}+D_{\text {d-online}}>0$.

Under the fixed-fee contract, the profit functions are as follows:

$$\begin{aligned} \pi _{m}(p_1,p_2)= & {} p_1D_{\text {BM}}+(p_2-r)D_{\text {s-online}}+ (p_2-r-u)D_{\text {d-online}} \\&- C \text { and } \pi _r(r) = r(D_{\text {s-online}}+D_{\text {d-online}}). \end{aligned}$$

Because the formal analysis of this model is complicated and we cannot find any analytical results regarding the contract choice of the online retailer, we have to perform numerical experiments to compute the equilibrium results. For our numerical experiments, $t=0.001$, $\overline{\lambda } = 0.1$, $\overline{r} = 0.04$, $\theta =0.75$, $\gamma =0.8$, $C=0.08$, $\hat{p} = 0.5$, and $u = 0.01$. If the online retailer adopts the revenue-sharing contract, then we obtain $\pi _r(\lambda ) = 0.000506667$, $\pi _{m}(p,s) = 0.16936$, $p_1=0.51$, and $p_2=0.38$. If the online retailer adopts the fixed-fee contract, then we obtain $\pi _r(\lambda ) = 0.000533333$, $\pi _{m}(p,s) = 0.169333$, $p_1=0.51$, and $p_2=0.38$. Thus, the online retailer’s profit under the revenue-sharing contract is less than that under the fixed-fee contract, which implies that the online retailer may adopt the fixed-fee contract to maximize her profit. This completes the proof of Corollary 3.

Table 14 Demands for the products through different channels