Electricity pricing, capacity, and predictive maintenance considering reliability

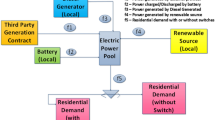
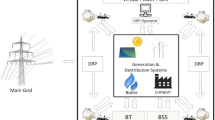
Abstract

Operations and maintenance management for renewable energy (RE) projects has become increasingly important in improving energy system models’ precision. Specifically, some elements are uncertain and difficult to predict, such as temperature conditions or system reliability, and these result in more complicated RE projects. Suitable maintenance and insurance policies are vital to reduce risks for RE system operators. This paper formulates a profit model that integrates system reliability, predictive maintenance, and green insurance into electricity pricing and capacity problems. A non-linear optimization solution procedure is proposed to determine the optimal electricity price, capacity, investment plan, predictive maintenance budget, and insurance level while maximizing company profit. The theoretical results indicate that RE systems’ increased reliability decreases the insurance level. However, an increase in the insurance level decreases RE project investments. Therefore, companies can attract more investments for RE projects if RE system reliability increases while insurance costs decrease. Additionally, this work not only presents a numerical analysis with examples and a sensitivity analysis to illustrate the model, but also discusses the opportunities this work offers for managers and analysts in practice.

Appendix

Proposition 1

We set out to establish the KKT conditions for the power company’s constrained maximization problem for renewable energy system. We begin with the Lagrangian of $E(\prod_{t} )$ for time t as

$$ \begin{aligned} \ell \left( {P_{t} ,K_{t} ,L_{t} ,M_{t} ,\tau_{t} ,\mu_{t}^{1} ,\mu_{t}^{2} } \right) = & E\left( {\prod_{t} } \right) + \mu_{t}^{1} \left( {0 - \overline{R} + \Pr \;(K_{t}^{\alpha } L_{t}^{\beta } > D_{t} ) + be^{{\gamma M_{t} }} } \right) \\ & + \mu_{t}^{2} \left( {1 - \Pr \;(K_{t}^{\alpha } L_{t}^{\beta } > D_{t} ) - be^{{\gamma M_{t} }} } \right) \\ \end{aligned} $$

(A1)

where $\mu_{t}^{1}$ and $\mu_{t}^{2}$ is the Lagrange multipliers. Note that we don’t consider electricity storage, thus the decision at time t are independent with the one at time t + 1. We have the first-order necessary conditions (KKT) nonlinear optimization:

$$ \frac{\partial \ell }{{\partial P_{t} }} = P_{t}^{ - 1 - h} \left( {AP_{t}^{1 + h} + g_{t} \left( {\left( {h - 1} \right)P_{t} + h\left( {R_{t}^{M} - 1} \right)\left( {p^{NRE} + \rho c_{ce} } \right)} \right)} \right) = 0. $$

(A2)

$$ \frac{\partial \ell }{{\partial K_{t} }} = c^{K} I_{e}^{{\tau_{t} }} \left( {R_{t}^{M} - 1} \right) - R_{t}^{M} \left( {c^{K} - \beta \rho c_{ce} K_{t}^{\alpha - 1} L_{t}^{\beta } } \right) - c^{K} \tau_{t} = 0 $$

(A3)

$$ \frac{\partial \ell }{{\partial L_{t} }} = c^{L} I_{e}^{{\tau_{t} }} \left( {R_{t}^{M} - 1} \right) - R_{t}^{M} \left( {c^{L} - \beta \rho c_{ce} K_{t}^{\alpha } L_{t}^{\beta - 1} } \right) - c^{L} \tau_{t} = 0 $$

(A4)

$$ \frac{\partial \ell }{{\partial M_{t} }} = \left[ {\begin{array}{*{20}l} {\gamma \mu_{t} be^{{\gamma M_{t} }} - 1 - \gamma be^{{\gamma M_{t} }} \left( {c^{K} K_{t} + c^{L} L_{t} - c_{ce} \rho K_{t}^{\alpha } L_{t}^{\beta } } \right)} \hfill \\ { + \;\gamma be^{{\gamma M_{t} }} \left( {c^{cm} + I_{e}^{{\tau_{t} }} \left( {c^{K} K_{t} + c^{L} L_{t} } \right) + \left( {A - g_{t} P_{t}^{ - h} } \right)p^{NRE} + \rho c^{cm} \left( {A - g_{t} P_{t}^{ - h} } \right)} \right)} \hfill \\ \end{array} } \right] = 0 $$

(A5)

$$ \frac{\partial \ell }{{\partial \tau_{t} }} = - I_{e}^{{\tau_{t} }} \left( {c^{K} K_{t} + c^{L} L_{t} } \right)\left( {R_{t}^{M} - 1 + e^{{\tau_{t} }} } \right) = 0 $$

(A6)

$$ \frac{\partial \ell }{{\partial \mu_{t}^{1} }} = \mu_{t}^{1} \left( {R_{t}^{M} - \overline{R}} \right) = 0 $$

(A7)

$$ \frac{\partial \ell }{{\partial \mu_{t}^{2} }} = \mu_{t}^{2} \left( {1 - R_{t}^{M} } \right) = 0 $$

(A8)

where $P_{t} \ge 0,K_{t} \ge 0,L_{t} \ge 0,M_{t} \ge 0,\tau_{t} \ge 0,\mu_{t}^{1} \ge 0,\mu_{t}^{2} \ge 0$ and with $R_{t}^{M} = \Pr \;(K_{t}^{\alpha } L_{t}^{\beta } > D_{t} ) + be^{{\gamma M_{t} }}$ and $\mu_{t}^{1}$ and $\mu_{t}^{2}$ are the Lagrange multipliers. The resulting systems are solved to find the optimal values, from which the proposition follows. The KKT necessary conditions are sufficient to guarantee a global maximum policy for the company.