Using neural networks and support vector regression to relate marchetti dilatometer test parameters and maximum shear modulus

Abstract

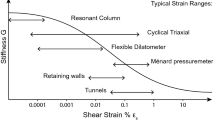
In the last two decades, small strain shear modulus became one of the most important geotechnical parameters to characterize soil stiffness. Finite element analysis have shown that in-situ stiffness of soils and rocks is much higher than what was previously thought and that stress-strain behaviour of these materials is non-linear in most cases with small strain levels, especially in the ground around retaining walls, foundations and tunnels, typically in the order of 10⁻² to 10⁻⁴ of strain. Although the best approach to estimate shear modulus seems to be based in measuring seismic wave velocities, deriving the parameter through correlations with in-situ tests is usually considered very useful for design practice.The use of Neural Networks for modeling systems has been widespread, in particular within areas where the great amount of available data and the complexity of the systems keeps the problem very unfriendly to treat following traditional data analysis methodologies. In this work, the use of Neural Networks and Support Vector Regression is proposed to estimate small strain shear modulus for sedimentary soils from the basic or intermediate parameters derived from Marchetti Dilatometer Test. The results are discussed and compared with some of the most common available methodologies for this evaluation.