Abstract
Schema theory is the most well-known model of evolutionary algorithms. Imitating from genetic algorithms (GA), nearly all schemata defined for genetic programming (GP) refer to a set of points in the search space that share some syntactic characteristics. In GP, syntactically similar individuals do not necessarily have similar semantics. The instances of a syntactic schema do not behave similarly, hence the corresponding schema theory becomes unreliable. Therefore, these theories have been rarely used to improve the performance of GP. The main objective of this study is to propose a schema theory which could be a more realistic model for GP and could be potentially employed for improving GP in practice. To achieve this aim, the concept of semantic schema is introduced. This schema partitions the search space according to semantics of trees, regardless of their syntactic variety. We interpret the semantics of a tree in terms of the mutual information between its output and the target. The semantic schema is characterized by a set of semantic building blocks and their joint probability distribution. After introducing the semantic building blocks, an algorithm for finding them in a given population is presented. An extraction method that looks for the most significant schema of the population is provided. Moreover, an exact microscopic schema theorem is suggested that predicts the expected number of schema samples in the next generation. Experimental results demonstrate the capability of the proposed schema definition in representing the semantics of the schema instances. It is also revealed that the semantic schema theorem estimation is more realistic than previously defined schemata.










Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Notes
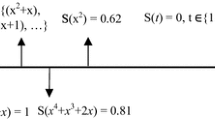
In the rest of the paper, we use “ =” for referring to “don’t care” symbol that is matched by a single terminal or function character and “#” for “don’t care” symbol that is matched by any valid subtree, consistently.
References
Koza JR (1992) Genetic programming: on the programming of computers by means of natural selection. MIT Press, p 680
Koza JR (2010) Human-competitive results produced by genetic programming. Genet Program Evolvable Mach 11(3–4):251– 284
Poli R, Langdon WB (1997) A New Schema Theory for Genetic Programming with One-point Crossover and Point Mutation. In: Genetic Programming 1997: Proceedings of the Second Annual Conference. Morgan Kaufmann
Poli R et al (2010) Theoretical results in genetic programming: the next ten years?. Genet Program Evolvable Mach 11(3):285–320
Holland JH (1992) Adaptation in natural and artificial systems. MIT Press, p 211
Altenberg L (1994) The evolution of evolvability in genetic programming. In: Advances in genetic programming. MIT Press, pp 47–74
Poli R, McPhee NF (2003) General schema theory for genetic programming with subtree-swapping crossover: Part II. Evol Comput 11(2):169–206
Poli R, McPhee NF (2003) General schema theory for genetic programming with subtree-swapping crossover: Part I. Evol Comput 11(1):53–66
Rosca JP (1997) Analysis of complexity drift in genetic programming. In: Genetic Programming 1997: Proceedings of the Second Annual Conference. Morgan Kaufmann, Stanford University, CA, USA
Poli R (2000) Exact schema theorem and effective fitness for GP with one-point crossover. In: Proceedings of the genetic and evolutionary computation conference. Morgan Kaufmann, Las Vegas
Poli R et al (2000) Hyperschema theory for GP with one-point crossover, building blocks, and some new results in GA theory. In: Genetic Programming. Springer, Heidelberg, pp 163– 180
Altenberg L (1994) Emergent phenomena in genetic programming. Evolutionary Programming–Proceedings of the Third Annual Conference:233–241
O’Reilly UM, Oppacher F (1994) The troubling aspects of a building block hypothesis for genetic programming. In: Foundations of genetic algorithms 3. Morgan Kaufmann, Estes Park
Whigham PA (1995) A schema theorem for context-free grammars. In: IEEE Conference on Evolutionary Computation. IEEE Press, Perth
Poli R (2001) Exact schema theory for genetic programming and variable-length genetic algorithms with one-point crossover. Genet Program Evolvable Mach 2(2):123–163
Poli R, McPhee N, Rowe J (2004) Exact schema theory and markov chain models for genetic programming and variable-length genetic algorithms with homologous crossover. Genet Program Evolvable Mach 5(1):31–70
Smart W, Andreae P, Zhang M (2007) Empirical analysis of GP tree-fragments. In: Proceedings of the 10th European conference on Genetic programming. Springer, Valencia, pp 55–67
Rosca JP, Ballard DH (1995) Causality in genetic programming. In: Proceedings of the 6th international conference on genetic algorithms. Morgan Kaufmann Publishers Inc
Haynes T (1997) Phenotypical building blocks for genetic programming. In: Genetic algorithms: proceedings of the seventh international conference. Michigan State University, Morgan Kaufmann, East Lansing
Majeed H (2005) A new approach to evaluate GP schema in context. In: Proceedings of the 2005 workshops on Genetic and evolutionary computation. ACM Press, Washington, pp 378– 381
Poli R, Langdon WB (1997) An experimental analysis of schema creation, propagation and disruption in genetic programming. In: Genetic algorithms: proceedings of the seventh international conference. Morgan Kaufmann
Poli R, Langdon WB (1998) Schema theory for genetic programming with one-point crossover and point mutation. Evol Comput 6(3):231–252
Poli R (2001) General schema theory for genetic programming with subtree-swapping crossover. In: Miller J et al (eds) Genetic programming. Springer, Berlin, pp 143–159
Altenberg L (1995) The schema theorem and price’s theorem. In: Foundations of genetic algorithms 3. Morgan Kaufmann
Smart W, Zhang M (2008) Empirical analysis of schemata in genetic programming using maximal schemata and MSG. In: Evolutionary Computation, 2008. IEEE Congress on CEC 2008.(IEEE World Congress on Computational Intelligence). IEEE
Whigham PA (1996) Search bias, language bias and genetic programming. In: Proceedings of the first annual conference on genetic programming. MIT Press
Rosca JP, Ballard DH (1999) Rooted-tree schemata in genetic programming. In: Advances in genetic programming. MIT Press, pp 243–271
Poli R, McPhee NF (2001) Exact schema theorems for GP with one-point and standard crossover operating on linear structures and their application to the study of the evolution of size. In: Genetic programming, proceedings of EuroGP’2001. Springer, Lake Como, pp 126–142
Poli R, McPhee NF (2001) Exact schema theory for GP and variable-length GAs with homologous crossover. COGNITIVE SCIENCE RESEARCH PAPERS-UNIVERSITY OF BIRMINGHAM CSRP
Poli R, McPhee NF (2001) Exact GP schema theory for headless chicken crossover and subtree mutation. in Proceedings of the 2001 Congress on Evolutionary Computation, 2001
Li G, Lee KH, Leung KS (2005) Evolve schema directly using instruction matrix based genetic programming. In: Proceedings of the 8th European conference on Genetic Programming. Springer, Lausanne, pp 271–280
Li G, Lee KH, Leung KS (2007) Using instruction matrix based genetic programming to evolve programs. In: Advances in computation and intelligence. Springer, pp 631–640
Larrañaga P, Lozano JA (2002) Estimation of distribution algorithms: a new tool for evolutionary computation, vol 2. Springer Science & Business Media
McPhee NF, Poli R (2002) Using schema theory to explore interactions of multiple operators. In: GECCO 2002: proceedings of the genetic and evolutionary computation conference. Morgan Kaufmann Publishers Inc., New York, pp 853– 860
Card S, Mohan C (2008) Towards an information theoretic framework for genetic programming. In: Riolo R, Soule T, Worzel B (eds) Genetic programming theory and practice V. Springer, USA, pp 87–106
Kraskov A, Stögbauer H, Grassberger P (2004) Estimating mutual information. Phys Rev E 69 (6):066138
Amir Haeri M, Ebadzadeh M (2014) Estimation of mutual information by the fuzzy histogram. Fuzzy Optim Decis Making 13(3):287–318
Aguirre AH, Coello Coello CA (2004). Mutual information-based fitness functions for evolutionary circuit synthesis. In: Evolutionary computation, 2004. Congress on CEC2004
Card SW (2011) Towards an information theoretic framework for evolutionary learning. In: Electrical engineering and computer science
Card SW, Mohan CK (2005) Information theoretic indicators of fitness, relevant diversity & pairing potential in genetic programming. In: The 2005 IEEE congress on evolutionary computation, 2005
Goldberg DE (1989) Genetic algorithms in search, optimization and machine learning. Addison-Wesley Longman Publishing Co., Inc, p 372
Rosca JP, Ballard DH (1996) Discovery of subroutines in genetic programming. In: Advances in genetic programming. MIT Press, pp 177–201
Sastry K et al Building block supply in genetic programming. In: Riolo RL, Worzel B (eds) Genetic programming theory and practice. Kluwer, pp 137–154
Kinzett D, Zhang M, Johnston M (2010) Analysis of building blocks with numerical simplification in genetic programming. In: Esparcia-Alcázar A et al (eds) Genetic programming. Springer, Berlin, pp 289–300
McKay RI et al (2009) Estimating the distribution and propagation of genetic programming building blocks through tree compression. In: Proceedings of the 11th annual conference on genetic and evolutionary computation. ACM
Tackett WA (1995) Mining the genetic program. IEEE expert: intelligent systems and their applications 10 (3):28–38
Langdon W, Banzhaf W (2005) Repeated sequences in linear genetic programming genomes. Complex Systems
Wilson GC, Heywood MI (2005) Context-Based repeated sequences in linear genetic programming. In: Proceedings of the 8th European conference on Genetic Programming. Springer, Lausanne, pp 240–249
Langdon WB, Banzhaf W (2008) Repeated patterns in genetic programming. Nat Comput 7(4):589–613
Shan Y et al (2006) A survey of probabilistic model building genetic programming. In: Scalable optimization via probabilistic modeling. Springer, Berlin, pp 121–160
Salton G, Wong A, Yang CS (1975) A vector space model for automatic indexing. Commun ACM 18 (11):613–620
Poli R, Stephens CR (2005) The building block basis for genetic programming and variable-length genetic algorithms. Int J Comput Intell Res 1(2):183–197
Uy NQ et al (2011) Semantically-based crossover in genetic programming: application to real-valued symbolic regression. Genet Program Evolvable Mach 12(2):91–119
Keijzer M (2003) Improving symbolic regression with interval arithmetic and linear scaling. In: Ryan C et al (eds) Genetic Programming. Springer, Berlin, pp 70–82
Vladislavleva EJ, Smits GF, den Hertog D (2009) Order of nonlinearity as a complexity measure for models generated by symbolic regression via Pareto genetic programming. IEEE Trans Evol Comput 13(2):333–349
McDermott J et al (2012) Genetic programming needs better benchmarks. In: Proceedings of the 14th annual conference on Genetic and evolutionary computation. ACM
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Zojaji, Z., Ebadzadeh, M.M. Semantic schema theory for genetic programming. Appl Intell 44, 67–87 (2016). https://doi.org/10.1007/s10489-015-0696-4
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10489-015-0696-4