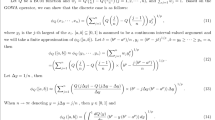Skip to main content

Advertisement

Springer Nature Link
Log in

Intuitionistic fuzzy hybrid arithmetic and geometric aggregation operators for the decision-making of mechanical design schemes

  • Published:
Applied Intelligence Aims and scope Submit manuscript

Abstract

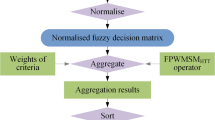
Arithmetic aggregation operators and geometric aggregation operators of intuitionistic fuzzy values (IFVs) are common aggregation operators in the fields of information fusion and decision making. However, their aggregated values imply some unreasonable results in some cases. To overcome the shortcomings, this paper proposes an intuitionistic fuzzy hybrid weighted arithmetic and geometric aggregation (IFHWAGA) operator and an intuitionistic fuzzy hybrid ordered weighted arithmetic and geometric aggregation (IFHOWAGA) operator and discusses their suitability by numerical examples. Then, we propose a multiple attribute decision-making method of mechanical design schemes based on the IFHWAGA or IFHOWAGA operator under an intuitionistic fuzzy environment. Finally, a decision-making problem regarding the mechanical design schemes of press machine is provided as a case to show the application of the proposed method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

References

  1. Atanassov KT (1986) Intuitionistic fuzzy set. Fuzzy Sets Syst 20:87–96

    Article  MATH  Google Scholar 

  2. Zadeh LA (1965) Fuzzy sets. Inf Control 8:338–356

    Article  MATH  Google Scholar 

  3. Li DF (2004) Some measures of dissimilarity in intuitionistic fuzzy structures. J Comput Syst Sci 68:115–122

    Article  MathSciNet  MATH  Google Scholar 

  4. Xu ZS, Yager RR (2006) Some geometric aggregation operators based on intuitionistic fuzzy sets. Int J Gen Syst 35:417– 433

    Article  MathSciNet  MATH  Google Scholar 

  5. Liu HW, Wang GJ (2007) Multi-attribute decision-making methods based on intuitionistic fuzzy sets. Eur J Oper Res 179:220–233

    Article  MATH  Google Scholar 

  6. Lin L, Yuan XH, Xia ZQ (2007) Multicriteria fuzzy decision-making methods based on intuitionistic fuzzy sets. J Comput Syst Sci 73:84–88

    Article  MathSciNet  MATH  Google Scholar 

  7. Xu ZS (2007) Intuitionistic fuzzy aggregation operators. IEEE Trans Fuzzy Syst 15:1179–1187

    Article  Google Scholar 

  8. Xu ZS (2007) Some similarity measures of intuitionistic fuzzy sets and their applications to multiple attribute decision making. Fuzzy Optim Decis Making 6:109–121

    Article  MathSciNet  MATH  Google Scholar 

  9. Xu ZS, Yager RR (2008) Dynamic intuitionistic fuzzy multi-attribute decision making. Int J Approx Reason 48:246–262

    Article  MATH  Google Scholar 

  10. Li DF (2008) Extension of the LINMAP for multi-attribute decision making under Atanassov’s intuitionistic fuzzy environment. Fuzzy Optim Decis Making 7:7–34

    Google Scholar 

  11. Wei GW (2008) Maximizing deviation method for multiple attribute decision making in intuitionistic fuzzy setting. Knowl-Based Syst 21:833–836

    Article  Google Scholar 

  12. Gong ZW, Li LS, Zhou FX, Yai TX (2009) Goal programming approaches to obtain the priority vectors from the intuitionistic fuzzy preference relations. Comput Ind Eng 57:1187–1193

    Article  Google Scholar 

  13. Wei GW (2010) GRA Method for multiple attribute decision making with incomplete weight information in intuitionistic fuzzy setting. Knowl-Based Syst 23:243–247

    Article  Google Scholar 

  14. Wei GW (2010) Some induced geometric aggregation operators with intuitionistic fuzzy information and their application to group decision making. Appl Soft Comput 10:423–431

    Article  Google Scholar 

  15. Xu ZS, Hu H (2010) Projection models for intuitionistic fuzzy multiple attribute decision making. Int J Inf Technol Decis Mak 9(2):267–280

    Article  MATH  Google Scholar 

  16. Ye J (2010) Fuzzy decision-making method based on the weighted correlation coefficient under intuitionistic fuzzy environment. Eur J Oper Res 205:202–204

    Article  MATH  Google Scholar 

  17. Ye J (2013) Multiple attribute group decision-making methods with completely unknown weights in intuitionistic fuzzy setting and interval-valued intuitionistic fuzzy setting. Group Decis Negot 22(2):173–188

    Article  MATH  Google Scholar 

  18. Ye J (2016) Similarity measures of intuitionistic fuzzy sets based on cosine function for the decision making of mechanical design schemes. J Intell Fuzzy Syst 30:151–158

    Article  MATH  Google Scholar 

  19. Xu YJ, Wang HM (2012) The induced generalized aggregation operators for intuitionistic fuzzy sets and their application in group decision making. Appl Soft Comput 12(3):1168–1179

    Article  Google Scholar 

  20. Yu XH, Xu ZS (2013) Prioritized intuitionistic fuzzy aggregation operators. Inform Fusion 14(1):108–116

    Article  Google Scholar 

  21. Zhao XF, Wei GW (2013) Some intuitionistic fuzzy Einstein hybrid aggregation operators and their application to multiple attribute decision making. Knowl-Based Syst 37:472–479

    Article  Google Scholar 

  22. Chen SM, Tan JM (1994) Handling multi-criteria fuzzy decision making problems based on vague set theory. Fuzzy Sets Syst 67:163–172

    Article  MATH  Google Scholar 

  23. Hong DH, Choi CH (2000) Multi-criteria fuzzy decision-making problems based on vague set theory. Fuzzy Sets Syst 114:103–113

    Article  MATH  Google Scholar 

  24. Ye J (2016) Similarity measures of intuitionistic fuzzy sets based on cosine function for the decision making of mechanical design schemes. J Intell Fuzzy Syst 30:151–158

    Article  MATH  Google Scholar 

Download references

Acknowledgments

The author very appreciates the editor’s suggestion and the anonymous reviewers’ comments that have helped improve my manuscript greatly.

Author information

Authors and Affiliations

  1. Department of Electrical and Information Engineering, Shaoxing University, 508 Huancheng West Road, Shaoxing, Zhejiang Province, 312000, People’s Republic of China

    Jun Ye

Authors
  1. Jun Ye
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Jun Ye.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ye, J. Intuitionistic fuzzy hybrid arithmetic and geometric aggregation operators for the decision-making of mechanical design schemes. Appl Intell 47, 743–751 (2017). https://doi.org/10.1007/s10489-017-0930-3

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10489-017-0930-3

Keywords