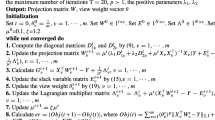Abstract
Multiview feature selection technique is specifically designed to reduce the dimensionality of multiview data and has received much attention. Most proposed multiview supervised feature selection methods suffer from the problem of efficiently handling the large-scale and high-dimensional data. To address this, this paper designs an efficient supervised multiview feature selection method for multiclass problems by combining the distributed optimization method in the Alternating Direction Method of Multipliers (ADMM). Specifically, the distributed strategy is reflected in two aspects. On the one hand, a sample-partition based distributed strategy is adopted, which calculates the loss term of each category individually. On the other hand, a view-partition based distributed strategy is used to explore the consistent and characteristic information of views. We adopt the individual regularization on each view and the common loss term which is obtained by fusing different views to jointly share the label matrix. Benefited from the distributed framework, the model can realize a distributed solution for the transformation matrix and reduce the complexity for multiview feature selection. Extensive experiments have demonstrated that the proposed method achieves a great improvement on training time, and the comparable or better performance compared to several state-of-the-art supervised feature selection algorithms.






Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Notes
Ads is an unbalanced dataset, classification accuracy obtained by SVM may not work. So we use F1 scores as the evaluation criterion on Ads dataset when adopting the SVM classifier.
References
Boyd S, Parikh N, Chu E, Peleato B, Eckstein J (2011) Distributed optimization and statistical learning via the alternating direction method of multipliers. Found Trends Mach Learn 3(1): 1–122
Cai X, Nie F, Huang H (2013) Exact top-k feature selection via l2,0-norm constraint. In: Proceedings of the Twenty-third International Joint Conference on Artificial Intelligence, pp 1240–1246
Cheng X, Zhu Y, Song J, Wen G, He W (2017) A novel low-rank hypergraph feature selection for multiview classification. Neurocomputing 253:115–121
Chua TS, Tang J, Hong R, Li H, Luo Z, Zheng Y (2009) NUS-WIDE: A Real-World Web Image Database from National University of Singapore. In: Proceedings of the ACM International Conference on Image and Video Retrieval, pp 368–375
Dalal N, Triggs B (2005) Histograms of oriented gradients for human detection. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp 886–893
Dua D, Graff C (2019) UCI Machine learning repository, University of California, School of Information and Computer Science. http://archive.ics.uci.edu/ml, Irvine
Feng Y, Xiao J, Zhuang Y, Liu X (2012) Adaptive unsupervised multi-view feature selection for visual concept recognition. In: Proceedings of the 11th Asian Conference on Computer Vision, pp. 343–357
Gui J, Sun Z, Ji S (2017) Feature selection based on structured sparsity: a comprehensive study. IEEE Trans Neural Netw Learn Syst 28(7):1490–1507
Hou C, Nie F, Tao H, Yi D (2017) Multi-view unsupervised feature selection with adaptive similarity and view weight. IEEE Trans Knowl Data Eng 29(9):1998–2011
Lan G, Hou C, Nie F, Luo T, Yi D (2018) Robust feature selection via simultaneous sapped norm and sparse regularizer minimization. Neurocomputing 283:228–240
Lee S, Park YT, d’Auriol BJ (2012) A novel feature selection method based on normalized mutual information. Appl Intell 37(1):100–120
Li Y, Shi X, Du C, Liu Y, Wen Y (2016) Manifold regularized multi-view feature selection for social image annotation. Neurocomputing 204:135–141
Lin Q, Xue Y, Wen J, Zhong P (2019) A sharing multi-view feature selection method via Alternating Direction Method of Multipliers. Neurocomputing 333:124–134
Lowe DG (2004) Distinctive image features from scale-invariant keypoints. Int J Comput Vis 60(2):91–110
Nene SA, Nayar SK, Murase H (1996) Columbia object image library (COIL-20)
Nie F, Huang H, Cai X, Ding C (2010) Efficient and robust feature selection via joint l2,1-norms minimization. In: Proceedings of the Advances in Neural Information Processing Systems, pp 1813–1821
Nie F, Li J, Li X (2017) Convex multiview semi-supervised classification. IEEE Trans Image Process 26(12):5718–5729
Ojala T, Pietikainen M, Maenpaa T (2002) Multiresolution gray-scale and rotation invariant texture classification with local binary patterns. IEEE Trans Pattern Anal Machine Intell 24(7):971–987
Oliva A, Torralba A (2001) Modeling the shape of the scene: a holistic representation of the spatial envelope. Int J Comput Vis 42(3):145–175
Shao W, He L, Lu C, Wei X, Yu P (2016) Online unsupervised multi-view feature selection. In: Proceedings of the IEEE 16th International Conference on Data Mining, pp 1203–1208
Shi C, Duan C, Gu Z, Tian Q, An G, Zhao R (2019) Semi-supervised feature selection analysis with structured multiview sparse regularization. Neurocomputing 330:412–424
Sindhwani V, Niyogi P, Belkin M (2005) A co-regularization approach to semi-supervised learning with multiple views. In: Proceedings of ICML workshop on Learning With Multiple Views, pp 74–79
Tang C, Chen J, Liu X, Li M, Wang P, Wang M, Lu P (2018) Consensus learning guided multiview unsupervised feature selection. Knowl-Based Syst 160:49–60
Tibshirani R (1996) Regression shrinkage and selection via the lasso. J R Stat Soc Series B Stat Methodol 58 (1):267–288
Tibshirani R, Saunders M, Rosset S, Zhu J, Knight K (2005) Sparsity and smoothness via the fused lasso. J R Stat Soc Ser B Stat Methodol 67(1):91–108
Tao H, Hou C, Nie F, Zhu J, Yi D (2017) Scalable multi-view semi-supervised classification via adaptive regression. IEEE Trans Image Process 26(9):4283–4296
Wang H, Nie F, Huang H (2011) Identifying quantitative trait loci via group-sparse multitask regression and feature selection: an imaging genetics study of the ADNI cohort. Bioinformatics 28(2):229–237
Wang H, Nie F, Huang H (2013) Multi-view clustering and feature learning via structured sparsity. In: Proceedings of the International Conference on Machine Learning, pp 352–360
Wang H, Nie F, Huang H, Ding C (2013) Heterogeneous visual features fusion via sparse multimodal machine. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp 3097–3102
Wang N, Xue Y, Lin Q, Zhong P (2019) Structured sparse multi-view feature selection based on weighted hinge loss. Multimed Tools Appl 78(11):15455–15481
Wang Z, Feng Y, Qi T, Yang X, Zhang J (2016) Adaptive multi-view feature selection for human motion retrieval. IET Signal Process 120:691–701
Xiao L, Sun Z, He R, Tan T (2013) Coupled feature selection for cross-sensor iris recognition. In: Proceedings of the IEEE Sixth International Conference on Biometrics: Theory, Applications and Systems (BTAS), pp 1–6
Xue X, Nie F, Wang S, Stantic B (2017) Multiview correlated feature learning by uncovering shared component. In: Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence
Yang M, Deng C, Nie F (2019) Adaptive-weighting discriminative regression for multiview classification. Pattern Recogn 88:236–245
Yang W, Gao Y, Cao L, Yang M, Shi Y (2014) mPadal: a joint local-and-global multi-view feature selection method for activity recognition. Appl Intell 41(3):776–790
Yang W, Gao Y, Shi Y, Cao L (2015) MRM-Lasso: A sparse multiview feature selection method via low-rank analysis. IEEE Trans Neural Netw Learn Syst 26(11):2801–2815
Yuan M, Lin Y (2006) Model selection and estimation in regression with grouped variables. J R Stat Soc Ser B Stat Methodol 68(1):49–67
You X, Xu J, Yuan W, Jing XY, Tao D, Zhang T (2019) Multi-view common component discriminant analysis for cross-view classification. Pattern Recogn 92:37–51
Zhang L, Lu X (2018) New fast feature selection methods based on multiple support vector data description. Appl Intell 48(7):1776–1790
Zhang Q, Tian Y, Yang Y, Pan C (2015) Automatic spatial spectral feature selection for hyperspectral image via discriminative sparse multimodal learning. IEEE Trans Geosci Remote Sens 53(1):261–279
Zhang R, Nie F, Li X (2017) Self-weighted supervised discriminative feature selection. IEEE Trans Neural Netw Learn Syst 29(8):3913–3918
Zhang Y, Li HG, Wang Q, Peng C (2019) A filter-based bare-bone particle swarm optimization algorithm for unsupervised feature selection. Appl Intell 49(8):2889–2898
Zhong J, Wang N, Lin Q, Zhong P (2019) Weighted feature selection via discriminative sparse multi-view learning. Knowl-Based Syst 178:132–148
Acknowledgments
The authors would like to thank the reviewers for their valuable comments and suggestions to improve the quality of this paper in advance.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
Theorem 2
Equations (16)-(19) is equivalent to (20)-(23).
Proof
-
1) For fixed i, the solution in (17) is obtained by updating V matrices \(\mathbf {Z}_{iv}\in \mathbb {R}^{n_{i}\times C}(v=1,2...V)\) with totally niCV variables. Now, we will carry it out by solving the (21) with only niC variables.
Let \(\overline {\mathbf {Z}_{i}}=\frac {1}{V}{\sum }_{v=1}^{V}\mathbf {Z}_{iv}\), the (17) can be rewritten as
$$ \begin{array}{@{}rcl@{}} \underset{\overline{\mathbf{Z}_{i}},\mathbf{Z}_{iv}}\min &&tr\left[\left( V\overline{\mathbf{Z}_{i}}-\mathbf{Y}_{i}\right)^{T}{\mathbf{F}_{i}}^{(k)} \left( V\overline{\mathbf{Z}_{i}}-\mathbf{Y}_{i}\right)\right]\\ &&\qquad+\frac{\rho}{2}\sum\limits_{v=1}^{V} \|\mathbf{Z}_{iv}-\mathbf{X}_{iv}{\mathbf{W}_{v}}^{(k+1)}+\frac{1}{\rho}{\mathbf{P}_{iv}}^{(k)}\|_{F}^{2}\\ s.t. && \overline{\mathbf{Z}_{i}}=\frac{1}{V}\sum\limits_{v=1}^{V}\mathbf{Z}_{iv} \end{array} $$(34)Minimizing over Ziv(v = 1, 2,...,V ) with \(\overline {\mathbf {Z}_{i}}\) fixed has the solution
$$ \mathbf{Z}_{iv}-\mathbf{X}_{iv}{\mathbf{W}_{v}}^{(k+1)}+\frac{1}{\rho}{\mathbf{P}_{iv}}^{(k)}=0 $$(35)Let \({\overline {\mathbf {X}_{i}\mathbf {W}}}=\frac {1}{V}{\sum }_{v=1}^{V} \mathbf {X}_{iv}{\mathbf {W}_{v}}, {\overline {\mathbf {P}_{i}}}=\frac {1}{V}{\sum }_{v=1}^{V} {\mathbf {P}_{iv}}\). Then, we have
$$ \overline{\mathbf{Z}_{i}}-\overline{\mathbf{X}_{i}\mathbf{W}}^{(k+1)}+\frac{1}{\rho}\overline{\mathbf{P}_{i}}^{(k)}=0 $$(36)Combining (35) and (36), we have
$$ \mathbf{Z}_{iv} = \mathbf{X}_{iv}{\mathbf{W}_{v}}^{(k+1)} - \frac{1}{\rho}{\mathbf{P}_{iv}}^{(k)} + \overline{\mathbf{Z}_{i}}-\overline{\mathbf{X}_{i}\mathbf{W}}^{(k+1)}+\frac{1}{\rho}\overline{\mathbf{P}_{i}}^{(k)} $$(37)Substituting (37) into (34),we get the following equation.
$$ \begin{array}{@{}rcl@{}} \underset{\overline{\mathbf{Z}_{i}}} \min && tr\left[\left( V\overline{\mathbf{Z}_{i}}-\mathbf{Y}_{i}\right)^{T}{\mathbf{F}_{i}}^{(k)}\left( V\overline{\mathbf{Z}_{i}}-\mathbf{Y}_{i}\right)\right]\\ &&+\frac{\rho V}{2}\|\overline{\mathbf{Z}_{i}}-\overline{\mathbf{X}_{i}\mathbf{W}}^{(k+1)}+\frac{1}{\rho} {\overline{\mathbf{P}_{i}}}^{(k)}\|_{F}^{2} \end{array} $$(38)Based on the above derivation, we can see that solving (17) is equivalent to solving (21).
-
2) Similarly, for fixed i, the Piv-update in (19) can be carried out by solving the (23) with only niC variables. Replacing Ziv in (37) with \({\mathbf {Z}_{iv}}^{(k+1)}\) obtains
$$ \begin{array}{@{}rcl@{}} {\mathbf{Z}_{iv}}^{(k+1)}&=&\mathbf{X}_{iv}{\mathbf{W}_{v}}^{(k+1)}-\frac{1}{\rho}{\mathbf{P}_{iv}}^{(k)}+\overline{\mathbf{Z}_{i}}^{(k+1)}\\ &&-\overline{\mathbf{X}_{i}\mathbf{W}}^{(k+1)} +\frac{1}{\rho}\overline{\mathbf{P}_{i}}^{(k)} \end{array} $$(39)Substituting (39) into (19) gives
$$ {\mathbf{P}_{iv}}^{(k+1)}=\rho\left( \overline{\mathbf{Z}_{i}}^{(k+1)}-\overline{\mathbf{X}_{i}\mathbf{W}}^{(k+1)}\right)+\overline{\mathbf{P}_{i}}^{(k)} $$(40)(40) shows that the variables \({\mathbf {P}_{iv}}^{(k+1)}(v=1,2,...,V)\) are all equal for fixed i. So we can get \({\mathbf {P}_{iv}}^{(k+1)}=\frac {1}{V}{\sum }_{v=1}^{V} {\mathbf {P}_{iv}}^{(k+1)}=\overline {\mathbf {P}_{i}}^{(k+1)}\). Then, we have
$$ \overline{\mathbf{P}_{i}}^{k+1}=\rho\left( \overline{\mathbf{Z}_{i}}^{(k+1)}-\overline{\mathbf{X}_{i}\mathbf{W}}^{(k+1)}\right)+\overline{\mathbf{P}_{i}}^{(k)} $$(41)Based on the above derivation, we can see that solving (19) is equivalent to solving (23).
-
3) By replacing Ziv in (37) with \({\mathbf {Z}_{iv}}^{(k)}\) and substituting \({\mathbf {Z}_{iv}}^{(k)}\) into (16), we have
$$ \begin{array}{@{}rcl@{}} {\mathbf{W}_{v}}^{(k+1)} &:=& \underset{\mathbf{W}_{v}}\arg \min \left( \lambda\|\mathbf{W}_{v}\|_{2,1} + \frac{\rho}{2}\sum\limits_{i=1}^{C}\|\mathbf{X}_{iv}\mathbf{W}_{v}\right.\\ &&\qquad\qquad \left. -\left( \vphantom{\frac{1}{\rho}}\mathbf{X}_{iv}{\mathbf{W}_{v}}^{(k)}+ \overline{\mathbf{Z}_{i}}^{(k)} - \overline{\mathbf{X}_{i}\mathbf{W}}^{(k)}\right.\right.\\ &&\qquad\qquad\left.\left. +\frac{1}{\rho}\overline{\mathbf{P}_{i}}^{(k)}\right)\|_{F}^{2}\vphantom{\sum\limits_{i=1}^{C}}\right) \end{array} $$(42)Based on the above derivation, we can see that solving (16) is equivalent to solving (20).
-
4) According to \(\overline {\mathbf {Z}_{i}}=\frac {1}{V}{\sum }_{v=1}^{V}\mathbf {Z}_{iv}\), we can see that solving (18) is equivalent to solving (22).
□
Rights and permissions
About this article
Cite this article
Men, M., Zhong, P., Wang, Z. et al. Distributed learning for supervised multiview feature selection. Appl Intell 50, 2749–2769 (2020). https://doi.org/10.1007/s10489-020-01683-7
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10489-020-01683-7