Skip to main content

Advertisement

Springer Nature Link
Log in

An improved bagging ensemble surrogate-assisted evolutionary algorithm for expensive many-objective optimization

  • Published:
Applied Intelligence Aims and scope Submit manuscript

Abstract

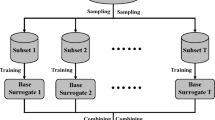
When the surrogate-assisted evolutionary algorithm is used to solve expensive many-objective optimization problems, the surrogate is used to approximate the expensive fitness functions. However, with the increase of the number of objectives, the approximate error of the surrogate will accumulate gradually, and the computational cost will also increase sharply. This paper proposes an improved bagging ensemble surrogate-assisted evolutionary algorithm (IBE-CSEA) to solve these problems. An ensemble classifier is used to classify the offspring instead of building the surrogate to approximate the fitness function of each objective. Firstly, a group of classification boundary individuals are selected one by one from the individuals evaluated by the expensive fitness function. All the individuals evaluated by the expensive fitness function are divided into two categories; Secondly, the individuals in these two categories are divided into the training set and the test set. The training set is used to train an improved bagging ensemble classifier. The test set is used to calculate the reliability of the classification; Finally, the classification results and the reliability are used to select the promising individuals for expensive fitness function evaluation. Compared with the current popular surrogate-assisted evolutionary algorithm, IBE-CSEA algorithm is more competitive.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

Data availability

The data used to support the findings of this study are available from the corresponding author upon request.

Abbreviations

ANN:

Artificial Neural Network

CPS-MOEA:

Classification and Pareto Domination based Multi-Objective Evolutionary Algorithm

CSEA:

Classification-based Surrogate-Assisted Evolutionary Algorithm

EA:

Evolutionary Algorithm

FE:

Fitness Evaluation

HV:

Hypervolume

IBE-CSEA:

Improved Bagging Ensemble Surrogate-Assisted Evolutionary Algorithm

IGD:

Inverse Generational Distance

K-RVEA:

Surrogate-Assisted Reference Vector Guided Evolutionary Algorithm

KTA2:

A Kriging-Assisted Two-Archive Evolutionary Algorithm

MAE:

Mean Absolute Error

MaOP:

Many-Objective Optimization Problem

MOEA/D-EGO:

Expensive Multi-Objective Optimization by MOEA/D with Gaussian Process Model

MOP:

Multi-Objective Optimization Problem

NSGA-III:

Evolutionary Many-Objective Optimization Algorithm Using Reference-Point-Based Nondominated Sorting Approach

PF:

Pareto Front

RMSE:

Root Mean Squared Error

SAEA:

Surrogate-Assisted Evolutionary Algorithm

c :

Categories of solution.

C Pi :

Model prediction results.

d :

The number of the decision variables.

d i :

Deviation between the predicted value and the true value.

FE max :

Maximum number of evaluations.

K :

The number of the classification boundary solutions.

M :

The number of objectives.

N :

Population size.

P :

Population.

p m :

Mutation probability.

P R :

Classification boundary.

Q :

offspring population.

Q c :

The set of group c solutions.

rr :

Proportion of group A solutions.

S :

Training set.

S’ :

Test set.

T :

Model pool size.

Ω :

Realized non-dominated solution set.

References

  1. Deb K, Jain H (2014) An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: solving problems with box constraints. IEEE Trans Evol Comput 18:577–601

    Article  Google Scholar 

  2. Zitzler E, Laumanns M, Thiele L (2001) SPEA2: improving the strength Pareto evolutionary algorithm. TIK-report, 103

  3. Gu Q, Chen H, Chen L (2001) A many-objective evolutionary algorithm with reference points-based strengthened dominance relation[J]. Inf Sci 554:236–255

    Article  MathSciNet  Google Scholar 

  4. Jin Y (2011) Surrogate-assisted evolutionary computation: recent advances and future challenges. Swarm Evolution Comput 1:61–70

    Article  Google Scholar 

  5. Zheng J (2018) An output mapping variable fidelity metamodeling approach based on nested Latin hypercube design for complex engineering design optimization. Appl Intell 48:3591–3611

    Article  Google Scholar 

  6. Jin Y, Sendhoff B (2009) A systems approach to evolutionary multiobjective structural optimization and beyond. IEEE Comput Intell Mag 4:62–76

    Article  Google Scholar 

  7. Douguet D (2010) E-LEA3D: a computational-aided drug design web server. Nucleic Acids Res 38:W615–W621

    Article  Google Scholar 

  8. Gu L, Yang RJ, Tho CH (2001) Optimisation and robustness for crashworthiness of side impact[J]. Int J Veh Des 26:348–360

    Article  Google Scholar 

  9. Gu Q, Wang Q, Li X (2021) A surrogate-assisted multi-objective particle swarm optimization of expensive constrained combinatorial optimization problems[J]. Knowl-Based Syst 223:107049

    Article  Google Scholar 

  10. Wilson B, Cappelleri D, Simpson TW, Frecker M (2001) Efficient Pareto frontier exploration using surrogate approximations. Optim Eng 2:31–50

    Article  MathSciNet  Google Scholar 

  11. Knowles J (2006) ParEGO: a hybrid algorithm with on-line landscape approximation for expensive multiobjective optimization problems. IEEE Trans Evol Comput 10:50–66

    Article  Google Scholar 

  12. Theil H (1992) A rank-invariant method of linear and polynomial regression analysis. In Henri Theil's contributions to economics and econometrics. Springer, Dordrecht, pp 345–381

    Google Scholar 

  13. Van Stein B, Wang H, Kowalczyk W (2020) Cluster-based kriging approximation algorithms for complexity reduction[J]. Appl Intell 50:778–791

    Article  Google Scholar 

  14. Dreiseitl S, Ohno-Machado L (2002) Logistic regression and artificial neural network classification models: a methodology review. J Biomed Inform 35:352–359

    Article  Google Scholar 

  15. Chugh T, Jin Y, Miettinen K (2018) A surrogate-assisted reference vector guided evolutionary algorithm for computationally expensive many-objective optimization[J]. IEEE Trans Evol Comput 22:129–142

    Article  Google Scholar 

  16. Zhang J, Zhou A, Zhang G (2015) A classification and Pareto domination based multiobjective evolutionary algorithm. In 2015 IEEE congress on evolutionary computation (CEC), pp 2883–2890

  17. Pan L, He C, Tian Y, Wang H, Zhang X, Jin Y (2018) A classification-based surrogate-assisted evolutionary algorithm for expensive many-objective optimization. IEEE Trans Evol Comput 23:74–88

    Article  Google Scholar 

  18. Böhning D (1992) Multinomial logistic regression algorithm. Ann Inst Stat Math 44:197–200

    Article  Google Scholar 

  19. Gu Q, Chang Y, Li X (2021) A novel F-SVM based on FOA for improving SVM performance[J]. Expert Syst Appl 165:113713

    Article  Google Scholar 

  20. Peterson LE (2009) K-nearest neighbor. Scholarpedia 4:1883

    Article  Google Scholar 

  21. Rokach L (2010) Ensemble-based classifiers. Artif Intell Rev 33:1–39

    Article  Google Scholar 

  22. Seni G, Elder JF (2010) Ensemble methods in data mining: improving accuracy through combining predictions[J]. Synthesis Lectures Data Mining Knowl Discovery 2:1–126

    Article  Google Scholar 

  23. Liu Y, Gong D, Sun J, Jin Y (2017) A many-objective evolutionary algorithm using a one-by-one selection strategy. IEEE Trans Cybern 47:2689–2702

    Article  Google Scholar 

  24. Sschapire RE (1999) A brief introduction to boosting. In Ijcai, pp 1401–1406

  25. Breiman L (1996) Bagging predictors. Mach Learn 24:123–140

    MATH  Google Scholar 

  26. Beasley D, Bull DR, Martin RR (1993) A sequential niche technique for multimodal function optimization. Evol Comput 1:101–125

    Article  Google Scholar 

  27. Helton JC, Davis FJ (2003) Latin hypercube sampling and the propagation of uncertainty in analyses of complex systems. Reliab Eng Syst Safety 81:23–69

    Article  Google Scholar 

  28. Zhou ZH, Wu J, Tang W (2002) Ensembling neural networks: many could be better than all[J]. Artif Intell 137(1–2):239–263

    Article  MathSciNet  Google Scholar 

  29. Dai Q, Yao CSA (2017) Hierarchical and parallel branch-and-bound ensemble selection algorithm[J]. Appl Intell 46:45–61

    Article  Google Scholar 

  30. Polikar R (2012) Ensemble learning[M]. Ensemble macshine learning. Springer, Boston, MA 1-34

  31. Zhang Y, Burer S, Nick Street W (2006) Ensemble Pruning Via Semi-definite Programming[J]. J Mach Learn Res 7(7)

  32. Levinson N (1946) The wiener (root mean square) error criterion in filter design and prediction. J Math Phys 25:261–278

    Article  MathSciNet  Google Scholar 

  33. Deb K, Thiele L, Laumanns M, Zitzler E (2005) Scalable test problems for evolutionary multiobjective optimization. In Evolutionary multiobjective optimization, pp 105–145

  34. Cheng R, Li M, Tian Y, Xiang X, Zhang X, Yang S (2018) Benchmark functions for the cec'2018 competition on many-objective optimization

  35. While L, Hingston P, Barone L, Huband S (2006) A faster algorithm for calculating hypervolume. IEEE Trans Evol Comput 10:29–38

    Article  Google Scholar 

  36. Zhang Q, Liu W, Tsang E, Virginas B (2009) Expensive multiobjective optimization by MOEA/D with Gaussian process model. IEEE Trans Evol Comput 14:456–474

    Article  Google Scholar 

  37. Song Z, Wang H, He C (2021) A kriging-assisted two-archive evolutionary algorithm for expensive many-objective optimization[J]. IEEE Trans Evol Comput, 1

Download references

Acknowledgments

This work was supported by National Natural Science Foundation of China [No.51774228]; Natural Science Foundation of Shaanxi Province of China [2020JC-44]; National Natural Science Foundation of China [No.51974223]; National Natural Science Foundation of China [No.52074205].

Author information

Author notes

  1. Xiaoyue Zhang contributed equally to this work.

Authors and Affiliations

  1. School of Management, Xi’an University of Architecture and Technology, Xi’an, China

    Qinghua Gu, Xiaoyue Zhang & Lu Chen

  2. Xi’an Key Laboratory for Intelligent Industrial Perception, Calculation and Decision, Xi’an University of Architecture and Technology, Xi’an, China

    Qinghua Gu, Xiaoyue Zhang & Lu Chen

  3. Department of Mathematics and Computer Science, Northeastern State University, Tahlequah, OK, USA

    Naixue Xiong

Authors
  1. Qinghua Gu
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Xiaoyue Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Lu Chen
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Naixue Xiong
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Qinghua Gu.

Ethics declarations

Conflict of interest

The authors declare that there are no conflicts of interest regarding the publication of this paper.

Additional information

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Gu, ., Zhang, X., Chen, L. et al. An improved bagging ensemble surrogate-assisted evolutionary algorithm for expensive many-objective optimization. Appl Intell 52, 5949–5965 (2022). https://doi.org/10.1007/s10489-021-02709-4

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10489-021-02709-4

Keywords