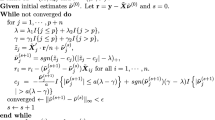Skip to main content
Springer Nature Link
Log in

A novel self-weighted Lasso and its safe screening rule

  • Published:
Applied Intelligence Aims and scope Submit manuscript

Abstract

Lasso is a popular method for high-dimensional applications in machine learning. In this paper, we propose a novel variant of Lasso, named self-weighted Lasso (SWL). Self-weighted means that the weights are obtained based on the correlations of features and output, which is only related to the data itself. SWL inherits the extraordinary properties of Lasso, which means that it has the function of feature selection and continuous shrinkage simultaneously. Meanwhile, SWL ensures that the solution is consistent for feature selection, which improves the performance of Lasso. However, there are still huge challenges when training large-scale data with SWL. To improve the efficiency of SWL, especially for large-scale and high-dimensional problems, we propose an efficient acceleration strategy. It belongs to the state-of-the-art safe screening methods, which can significantly reduce the training time without sacrificing the accuracy. Experimental results on twelve benchmark datasets and a practical dataset verify that the SWL has better performance in comparison with other state-of-the-art regression algorithms, and the proposed safe screening rule has excellent efficiency.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Tibshirani R (1996) Regression shrinkage and selection via the Lasso. J R Statist Soc Ser B 58 (1):267–288

    MathSciNet  MATH  Google Scholar 

  2. Chen SS, Donoho DL, Saunders MA (1998) Atomic decomposition by basis pursuit. SIAM J Sci Comput 20(1):33–61

    Article  MathSciNet  Google Scholar 

  3. Bruckstein AM, Donoho DL, Elad M (2009) From sparse solutions of systems of equations to sparse modeling of signals and images. SIAM Rev 51(1):34–81

    Article  MathSciNet  Google Scholar 

  4. Chen SB, Zhang YM, Ding CHQ, et al. (2019) Extended Adaptive Lasso for multi-class and multi-label feature selection. Knowledge-Based Systems 173:28–36

    Article  Google Scholar 

  5. Lee JD, Sun DL, Sun Y, Taylor JE (2016) Exact post-selection inference with application to the Lasso. The Annals of Statistics 44(3):907–927

    Article  MathSciNet  Google Scholar 

  6. Cui C, Wang D (2016) High dimensional data regression using Lasso model and neural networks with random weights. Inform Sci 372:505–517

    Article  Google Scholar 

  7. Zhao W, Beach TH, Rezgui Y (2019) Automated model construction for combined sewer overflow prediction based on efficient Lasso algorithm. IEEE Trans Syst Man Cybernet Systems 49(6):1254–1269

    Article  Google Scholar 

  8. Xie Z, Xu Y (2014) Sparse group LASSO based uncertain feature selection. Int J Mach Learn Cybern 5:201–210

    Article  Google Scholar 

  9. Donoho DL, Huo X (2001) Uncertainty principles and ideal atomic decomposition. IEEE Trans Inf Theo 47(7):2845–2862

    Article  MathSciNet  Google Scholar 

  10. Donoho DL, Elad M (2003) Optimally sparse representation in general (nonorthogonal) dictionaries via l1 minimization. Proceedings of the National Academy of Sciences 100(5):2197–2202

    Article  MathSciNet  Google Scholar 

  11. Donoho DL (2006) For most large underdetermined systems of linear equations the minimal l1-norm solution is also the sparsest solution. Comm Pure Appl Math 59(6):797–829

    Article  MathSciNet  Google Scholar 

  12. Meinshausen N, Bühlmann P (2006) High dimensional graphs and variable selection with the LASSO. Ann Statist 34(3):1436–1462

    Article  MathSciNet  Google Scholar 

  13. Leng C, Lin Y, Wahba G (2006) A note on the Lasso and related procedures in model selection. Statistica Sinica 16(4):1273–1284

    MathSciNet  MATH  Google Scholar 

  14. Zou H (2006) The Adaptive Lasso and its oracle properties. J American Statistical Association 101(476):1418–1429

    Article  MathSciNet  Google Scholar 

  15. Lian L, Liu A, Lau VK (2018) Weighted Lasso for sparse recovery with statistical prior support information. IEEE Trans Signal Process 66(6):1607–1618

    Article  MathSciNet  Google Scholar 

  16. Su M, Guo Y, Men C, Wang W (2019) A robust self-weighted SELO regression model. Int J Mach Learn Cybern 10:3189–3199

    Article  Google Scholar 

  17. Breheny P, Huang J (2011) Coordinate descent algorithms for nonconvex penalized regression, with applications to biological feature selection. Ann Statist 5(1):224–244

    MathSciNet  MATH  Google Scholar 

  18. Madigan D, Ridgeway G (2004) Least angle regression: Discussion. Ann Stat 32(2):465–469

    Google Scholar 

  19. Daubechies I, Defrise M, Mol CD (2004) An iterative thresholding algorithm for linear inverse problems with a sparsity constraint. Commun Pure Appl Math 57(11):1413–1457

    Article  MathSciNet  Google Scholar 

  20. Bioucas-Dias JM, Figueiredo MA (2007) A new twIST: Two-step iterative shrinkage/thresholding algorithms for image restoration. IEEE Trans Image Process 16(12):2992–3004

    Article  MathSciNet  Google Scholar 

  21. Ghaoui LE, Viallon V, Rabbani T (2012) Safe feature elimination in sparse supervised learning. Pac J Optim 8:667–698

    MathSciNet  MATH  Google Scholar 

  22. Bonnefoy A, Emiya V, Ralaivola L, Gribonval R (2015) Dynamic screening: accelerating first-order algorithms for the Lasso and group-Lasso. IEEE Trans Signal Process 63(19):5121–5132

    Article  MathSciNet  Google Scholar 

  23. Fercoq O, Gramfort A, Salmon J (2015) Mind the duality gap: safer rules for the Lasso. In: Advances in the 32nd international conference on machine learning, pp 333–342

  24. Liu J, Zhao Z, Wang J, Ye J (2014) Safe screening with variational inequalities and its application to Lasso. In: Advances in the 31th international conference on machine learning, pp 289–297

  25. Mei B, Xu Y (2020) Safe sample screening for regularized multi-task learning. Knowledge-Based Systems 204:106248

    Article  Google Scholar 

  26. Ndiaye E, Fercoq O, Gramfort A, Salmon J (2015) GAP safe screening rules for sparse multi-task and multi-class models. In: Advances in the 32th international conference on machine learning, pp 811–819

  27. Cao Y, Xu Y, Du J (2020) Multi-variable estimation-based safe screening rule for small sphere and large margin support vector machine. Knowledge-Based Systems 191:105223

    Article  Google Scholar 

  28. Shibagaki A, Karasuyama M, Hatano K, Takeuchi I (2016) Simultaneous safe screening of features and samples in doubly sparse modeling. In: Advances in the 33nd international conference on machine learning, pp 1577–1586

  29. Wang H, Xu Y (2018) Scaling up twin support vector regression with safe screening rule. Inform Sci 465:174–190

    Article  MathSciNet  Google Scholar 

  30. Wang J, Zhou J, Wonka P, Ye J (2013) Lasso screening rules via dual polytope projection. In: Advances in neural information processing systems, pp 1070–1078

  31. Zhang W, Hong B, Liu W, Ye J, Cai D, He X, Wang J (2017) Scaling up sparse support vector machines by simultaneous feature and sample reduction. In: Advances in the 34th international conference on machine learning, pp 4016–4025

  32. Wu W, Xu Y (2019) Accelerating improved twin support vector machine with safe screening rule. Int J Mach Learn Cybern 10:3587–3600

    Article  Google Scholar 

  33. Pan X, Pang X, Wang H, Xu Y (2018) A safe screening based framework for support vector regression. Neurocomputing 287:163–172

    Article  Google Scholar 

  34. Pan X, Yang Z, Xu Y, Wang L (2018) Safe screening rules for accelerating twin support vector machine classification. IEEE Trans Neural Netw Learn Syst 29(5):1876–1887

    Article  MathSciNet  Google Scholar 

  35. Wang H, Pan X, Xu Y (2019) Simultaneous safe feature and sample elimination for sparse support vector regression. IEEE Trans Signal Process 67(15):4043–4054

    Article  MathSciNet  Google Scholar 

  36. Boyd V (2006) Faybusovich, Convex optimization. IEEE Trans Automat Contr 51(11):1859–1859

    Article  Google Scholar 

  37. Beck A, Teboulle M (2009) A fast iterative Shrinkage-Thresholding algorithm for linear inverse problems. SIAM J Imaging Sci 2(1):183–202

    Article  MathSciNet  Google Scholar 

  38. Florea MI, Vorobyov SA (2017) A robust FISTA-like algorithm. In: 2017 IEEE international conference on acoustics, speech and signal processing (ICASSP), New Orleans, LA, pp 4521–4525

  39. Tang L, Tian Y, Yang C (2018) Nonparallel support vector regression model and its SMO-type solver. Neural Netw 105:431–446

    Article  Google Scholar 

  40. Rastogi R, Anand P, Chandra S (2017) L1-norm twin support vector machine-based regression. Optimization, pp 1–17

  41. Hamidieh K (2018) A data-driven statistical model for predicting the critical temperature of a superconductor. Comput Mater Sci 154:346–354

    Article  Google Scholar 

Download references

Acknowledgments

The authors would like to thank the reviewers for their valuable suggestions to improve this paper. This work was supported in part by the National Natural Science Foundation of China (NO. 12071475, 11671010) and in part by the Beijing Natural Science Foundation (NO. 4172035).

Author information

Authors and Affiliations

  1. College of Information and Electrical Engineering, China Agricultural University, Beijing, 100083, China

    Xinshuang Xiao & Ying Zhang

  2. College of Science, China Agricultural University, Beijing, 100083, China

    Yitian Xu & Peiwei Zhong

Authors
  1. Xinshuang Xiao
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Yitian Xu
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Ying Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Peiwei Zhong
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Yitian Xu.

Additional information

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Xiao, X., Xu, Y., Zhang, Y. et al. A novel self-weighted Lasso and its safe screening rule. Appl Intell 52, 14465–14477 (2022). https://doi.org/10.1007/s10489-022-03316-7

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10489-022-03316-7

Keywords