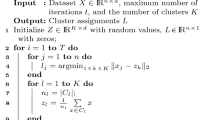Abstract
The K-means algorithm is widely applied for clustering, and its clustering effect is influenced by its initialization. However, most existing works focus on the initialization of K and centers in Euclidean spaces, but few works in the literature deal with the initialization of K-means clustering on Riemannian manifolds. In this paper, we propose a unified scheme for learning K and selecting the initial centers for intrinsic K-means clustering on homogeneous manifolds, which can also be generalized to other types of manifolds. First, geodesic verticality is presented based on the geometric properties abstracted from the definition of orthogonality in Euclidean spaces. Then, geodesic projection on Riemannian manifolds is proposed for learning K, which achieves nonlinear dimensionality reduction and improves the computing efficiency. Additionally, the Riemannian metric of \(\mathbb {S}^{n}\) is derived for the statistical initialization of the centers to improve the clustering accuracy. Finally, the intrinsic K-means algorithm for clustering on homogeneous manifolds based on the Karcher mean is given by applying the proposed manifold initialization, which improves the clustering effect. Simulations and experimental studies are conducted to show the effectiveness and accuracy of the proposed K-means scheme on manifolds.


















Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Lu W (2020) Improved k-means clustering algorithm for big data mining under hadoop parallel framework. J Grid Comput 18(2):239–250
Jaquier N, Rozo L, Caldwell DG, Calinon S (2021) Geometry-aware manipulability learning, tracking, and transfer. Int J Robot Res 40(2-3):624–650
Arthur D, Vassilvitskii S (2006) K-means++: the advantages of careful seeding. Tech rep, Stanford
Zhang W, Kong D, Wang S, Wang Z (2019) 3d human pose estimation from range images with depth difference and geodesic distance. J Vis Commun Image Represent 59:272–282
Yan Z, Duckett T, Bellotto N (2020) Online learning for 3d lidar-based human detection: experimental analysis of point cloud clustering and classification methods. Auton Robot 44(2):147–164
Borlea ID, Precup RE, Borlea AB, Iercan D (2021) A unified form of fuzzy c-means and k-means algorithms and its partitional implementation. Knowl-Based Syst 214:106731
Fränti P, Sieranoja S (2018) K-means properties on six clustering benchmark datasets. Appl Intell 48(12):4743–4759
Hamerly G, Elkan C (2003) Learning the k in k-means. Advances in neural information processing systems 16:281–288
Calinon S (2020) Gaussians on riemannian manifolds: applications for robot learning and adaptive control. IEEE Robot Autom Mag 27(2):33–45
Hechmi S, Gallas A, Zagrouba E (2019) Multi-kernel sparse subspace clustering on the riemannian manifold of symmetric positive definite matrices. Pattern Recogn Lett 125:21–27
Fathian K, Ramirez-Paredes JP, Doucette EA, Curtis JW, Gans NR (2018) Quest: a quaternion-based approach for camera motion estimation from minimal feature points. IEEE Robotics and Automation Letters 3(2):857–864
Zeestraten MJ, Havoutis I, Silvério J, Calinon S, Caldwell DG (2017) An approach for imitation learning on riemannian manifolds. IEEE Robot Automn Lett 2(3):1240–1247
Lang M, Hirche S (2017) Computationally efficient rigid-body gaussian process for motion dynamics. IEEE Robot Autom Lett 2(3):1601–1608
Absil PA, Mahony R, Sepulchre R (2009) Optimization algorithms on matrix manifolds. Princeton University Press
Pennec X, Fillard P, Ayache N (2006) A riemannian framework for tensor computing. Int J Comput Vis 66(1):41–66
Lin Z, Yao F (2019) Intrinsic riemannian functional data analysis. Ann Stat 47(6):3533–3577
Saha J, Mukherjee J (2021) Cnak: cluster number assisted k-means. Pattern Recogn 110:107625
Zhang T, Lin G (2021) Generalized k-means in glms with applications to the outbreak of covid-19 in the United States. Comput Stat Data Anal 159:107217
Wang F, Franco-Penya HH, Kelleher JD, Pugh J, Ross R (2017) An analysis of the application of simplified silhouette to the evaluation of k-means clustering validity. In: International conference on machine learning and data mining in pattern recognition. Springer, pp 291–305
Zhang G, Zhang C, Zhang H (2018) Improved k-means algorithm based on density canopy. Knowl-Based Syst 145:289–297
Nasser A, Hamad D, Nasr C (2006) K-means clustering algorithm in projected spaces. In: 2006 9Th international conference on information fusion. IEEE, pp 1–6
Zhou J, Pedrycz W, Yue X, Gao C, Lai Z, Wan J (2021) Projected fuzzy c-means clustering with locality preservation. Pattern Recogn 113:107748
Lasheng C, Yuqiang L (2017) Improved initial clustering center selection algorithm for k-means. In: 2017 Signal processing: algorithms, architectures, arrangements, and applications (SPA). IEEE, pp 275–279
Fränti P, Sieranoja S (2019) How much can k-means be improved by using better initialization and repeats? Pattern Recogn 93:95–112
Zhou P, Chen J, Fan M, Du L, Shen YD, Li X (2020) Unsupervised feature selection for balanced clustering. Knowl-Based Syst 193:105417
Torrente A, Romo J (2021) Initializing k-means clustering by bootstrap and data depth. J Classif 38(2):232–256
Fränti P (2018) Efficiency of random swap clustering. J Big Data 5(1):1–29
Tîrnăucă C, Gómez-Pérez D, Balcázar JL, Montaña JL (2018) Global optimality in k-means clustering. Inf Sci 439:79–94
Rahman MA, Islam MZ (2018) Application of a density based clustering technique on biomedical datasets. Appl Soft Comput 73:623–634
Limwattanapibool O, Arch-int S (2017) Determination of the appropriate parameters for k-means clustering using selection of region clusters based on density dbscan (srcd-dbscan). Expert Syst 34(3):e12204
Giovanis DG, Shields MD (2020) Data-driven surrogates for high dimensional models using gaussian process regression on the grassmann manifold. Comput Methods Appl Mech Eng 370:113269
Chien SH, Wang JH, Cheng MY (2020) Performance comparisons of different observer-based force-sensorless approaches for impedance control of collaborative robot manipulators. In: 2020 IEEE conference on industrial cyberphysical systems (ICPS), vol 1. IEEE, pp 326–331
Li H, Liu J, Yang Z, Liu RW, Wu K, Wan Y (2020) Adaptively constrained dynamic time warping for time series classification and clustering. Inf Sci 534:97–116
Acknowledgements
This work was supported by the National Natural Science Foundation of China under Grant No. 52090054 and 52188102, and Natural Science Foundation of Hubei Province, China under Grant No. 2020CFA077.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of Interests
The authors declare that they have no conflict of interest.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix:: Convergence of intrinsic K-means
Appendix:: Convergence of intrinsic K-means
The convergence of the proposed intrinsic K-means algorithm is crucial. The calculation to minimize objective function (6) is an NP-hard problem. This can be proven as follows.
Loss function
where Dnk = 1 if pn ∈ Dk; otherwise, Dnk = 0 and \({{|| {{{\text {Log}}_{{\mathbf {\mu }_{k}}}}{\mathbf {p}_{n}}} ||}} = {||{\text {Log}}_{\mathbf {e}} \mathbf {\mathcal {A}}_{\mathbf {e}}^{\mathbf {\mu }_{k}} \mathbf {p}_{n} ||_{\mathbf {\mu }_{k}}}\).
E-step
When we update D from Dt− 1 to Dt, the distance between points on the manifolds is determined by the Riemannian geodesic, and can be calculated by (5).
where \({|| {\text {Log}}_{{\mathbf {\mu }_{j}}}{\mathbf {p}_{n}} ||} = {||{\text {Log}}_{\mathbf {e}} \mathbf {\mathcal {A}}_{\mathbf {e}}^{\mathbf {\mu }_{j}} \mathbf {p}_{n} ||_{\mathbf {\mu }_{j}}}\); thus, we can obtain
where \({D^{(t)}} = \arg {\min \limits _{D}}L({\mathbf {\mu }^{(t - 1)}}, \mathbf {P}, D)\).
M-step
When we update μ from μ(t− 1) to μ(t), the current mean is determined by Karcher mean (Algorithm 3).
This is a decreasing process; thus, we can obtain
where \({\mathbf {\mu }^{(t)}} = \arg {\min \limits _{\mathbf {\mu }} }L(\mathbf {\mu } ,\mathbf {P},{D^{(t)}})\). Each iteration of the algorithm decreases the otherwise positive quantization error until the error reaches a fixed point.
Rights and permissions
About this article
Cite this article
Tan, C., Zhao, H. & Ding, H. Statistical initialization of intrinsic K-means clustering on homogeneous manifolds. Appl Intell 53, 4959–4978 (2023). https://doi.org/10.1007/s10489-022-03698-8
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10489-022-03698-8