A new population initialization approach based on Metropolis–Hastings (MH) method

Abstract

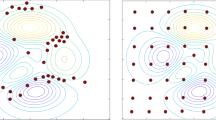
In this paper, a new population initialization method for metaheuristic algorithms is proposed. In our approach, the initial set of candidate solutions is obtained through the sampling of the objective function with the use of the Metropolis–Hastings technique. Under this method, the set of initial solutions adopts a value close to the prominent values of the objective function to be optimized. Different from most of the initialization methods that consider only spatial distribution, in our algorithm, the initial points represent promising regions of the search space, which deserve to be exploited to identify the global optimum. These characteristics allow the proposed approach obtains a faster convergence and improves the quality of the produced solutions. With the objective to demonstrate the capacities of our initialization method, it has been embedded in the classical Differential Evolution algorithm. To evaluate its performance, the complete system has been tested in a set of representative benchmark functions extracted from several datasets. Experimental results show that the proposed technique presents a better convergence speed and an increment in the quality of the solutions than other similar approaches.

Appendix A

	Name	MInimum	S	D	Function
f(x)1	Ackley	f(x∗) = 0; x∗ = (0, …, 0)	[−30, 30]d	30	$f(x)=-20\exp \left(-0.2\sqrt{\frac{1}{d}\sum \limits_{i=d}^d{x}_i^2}\right)-\exp \left(\frac{1}{d}\sum \limits_{i=1}^d\cos \left(2\pi {x}_i\right)\right)+\exp (1)+20$
f(x)2	Dixon-Price	f(x∗) = 0; ${\mathbf{x}}^{\ast}={2}^{-\frac{2^i-2}{2^i}}$ for i = 1, …, n	[−10, 10]d	30	$f(x)={\left({x}_1-1\right)}^2+\sum \limits_{i=2}^di{\left(2{x}_i^2-{x}_{i-1}\right)}^2$
f(x)3	Griewank	f(x∗) = 0; x∗ = (0, …, 0)	[−600, 600]d	30	$f(x)=\sum \limits_{i=1}^d\frac{x_i^2}{4000}-\prod \limits_{i=1}^d\cos \left(\frac{x_i}{\sqrt{i}}\right)+1$
f(x)4	Infinity	f(x∗) = 0; x∗ = (0, …, 0)	[−1, 1]d	30	$f(x)=\sum \limits_{i=1}^d{x}_i^6\left( sen\left({x}_i\right)+2\right)$
f(x)5	Levy	f(x∗) = 0; x∗ = (1, …, 1)	[−10, 10]d	30	$f(x)={\mathit{\sin}}^2\left(\pi {\omega}_1\right)+\sum \limits_i^{d-1}{\left({\omega}_1-1\right)}^2\left[1+10{\mathit{\sin}}^2\left(\pi {\omega}_i+1\right)\right]+{\left({\omega}_d-1\right)}^2\left[1+\right]{\mathit{\sin}}^2\left(2\pi {\omega}_d\right)$ $whre\kern0.5em {\omega}_i=1+\frac{x_i-1}{4}$
f(x)6	Mishra 1	f(x∗) = 2; x∗ = (1, …, 1)	[0, 1]d	30	$f(x)={\left(1+\left(d-\sum \limits_{i=1}^{d-1}{x}_i\right)\right)}^{d-\sum \limits_{i=1}^{d-1}{x}_i}$
f(x)7	Mishra 2	f(x∗) = 2; x∗ = (1, …, 1)	[0, 1]d	30	$f(x)={\left(1+\left(d-\sum \limits_{i=1}^{d-1}\frac{x_i+{x}_{i+1}}{2}\right)\right)}^{d-\sum \limits_{i=1}^{d-1}\left(\frac{x_i+{x}_{i+1}}{2}\right)}$
f(x)8	Mishra 11	f(x∗) = 0; x∗ = (0, …, 0)	[−10, 10]d	30	$f(x)={\left[\frac{1}{d}\sum \limits_{i=1}^d\left|{x}_i\right|-{\left(\prod \limits_{i=1}^d|{x}_i|\right)}^{\frac{1}{d}}\right]}^2$
f(x)9	MultiModal	f(x∗) = 0; x∗ = (0, …, 0)	[−10, 10]d	30	$f(x)=\sum \limits_{i=1}^d\mid {x}_i\mid \prod \limits_{i=1}^d\mid {x}_i\mid$
f(x)10	Penalty 1	f(x∗) = 0; x∗ = (−1, …, −1)	[−50, 50]d	30	$f(x)=\frac{\pi }{30}\left(10{\mathit{\sin}}^2\left(\pi {y}_1\right)+\sum \limits_{i=1}^{d-1}{\left({y}_i-1\right)}^2\left[1+10{\mathit{\sin}}^2\left(\pi {y}_{i+1}\right)\right]+{\left({y}_i-1\right)}^2\right)+\sum \limits_{i=1}^du\left({x}_i,\mathrm{10,100,4}\right)$ ${y}_i=1+\frac{x_i+1}{4},u\left({x}_i,a,k,m\right)\left\{\begin{array}{c}k{\left({x}_i-a\right)}^m\kern0.5em ,{x}_i>a\\ {}0\kern0.5em ,-a\le {x}_i\le a\\ {}\begin{array}{cc}k{\left(-{x}_i-a\right)}^m&, {x}_i<-a\end{array}\end{array}\right.$
f(x)11	Penalty 2	f(x∗) = 0; x∗ = (1, …, 1)	[−50, 50]d	30	$f(x)=0.1\left({\left(\mathit{\sin}\left(3\pi {x}_1\right)\right)}^2+\sum \limits_{i=1}^{d-1}{\left({x}_i-1\right)}^2\left[1+{\mathit{\sin}}^2\left(3\pi {x}_{i+1}\right)\right]+\left[{\left({x}_i-1\right)}^2{\left(\mathit{\sin}\left(2\pi {x}_i\right)\right)}^2\right]\right)+\sum \limits_{i=1}^du\left({x}_i,\mathrm{5,100,4}\right)$ $\kern0.5em u\left({x}_i,a,k,m\right)\left\{\begin{array}{c}k{\left({x}_i-a\right)}^m\kern0.5em ,{x}_i>a\\ {}\begin{array}{cc}0&, -a\le {x}_i\le a\end{array}\\ {}\begin{array}{cc}k{\left(-{x}_i-a\right)}^m&, {x}_i<-a\end{array}\end{array}\right.$
f(x)12	Perm 1	f(x∗) = 0; x∗ = (1, 2, …, n)	[−d, d]d	30	$f(x)=\sum \limits_{k=1}^d{\left[\sum \limits_{i=1}^d\left({i}^k+50\right)\left({\left(\frac{x_i}{i}\right)}^k-1\right)\right]}^2$
f(x)13	Perm 2	f(x∗) = 0; x∗ = (1, 1/2, …, 1/n)	[−d, d]d	30	$f(x)=\sum \limits_{i=1}^d{\left[\sum \limits_{j=1}^d\left({j}^i+10\right)\Big({\left({x}_j^i-\frac{1}{j^i}\right)}^i\right]}^2$
f(x)14	Plateau	f(x∗) = 30; x∗ = (0, …, 0)	[−5.12, 5.12]d	30	$f(x)=30+\sum \limits_{i=1}^d\mid {x}_i\mid$
f(x)15	Powell	f(x∗) = 0; x∗ = (0, …, 0)	[−4, 5]d	30	$f(x)=\sum \limits_{i=1}^{\frac{d}{4}}\left[{\left({x}_{4i-3}+10{x}_{4i-2}\right)}^2+5{\left({x}_{4i-1}-{x}_{4i}\right)}^2+{\left({x}_{4i-2}-{x}_{4i-1}\right)}^4+10{\left({x}_{4i-3}-{x}_{4i}\right)}^4\right]$
f(x)16	Quing	f(x∗) = 0; x∗ = (0, …, 0)	[−1.28, 1.28]d	30	$f(x)=\sum \limits_{i=1}^d{\left({x}_i^2-i\right)}^2$
f(x)17	Quartic	f(x∗) = 0; x∗ = (−1, …, −1)	[−10, 10]d	30	$f(x)=\sum \limits_{i=1}^di{x}_i^4+\mathit{\operatorname{rand}}\left[0,1\right)$
f(x)18	Quintic	f(x∗) = 0; x∗ = (0, …, 0)	[−5.12, 5.12]d	30	$f(x)=\sum \limits_{i=1}^d\mid {x}_i^5-3{x}_i^4+4{x}_i^3+2{x}_i^2-10{x}_i-4\mid$
f(x)19	Rastrigin	f(x∗) = 0; x∗ = (1, …, 1)	[−5, 10]d	30	$f(x)=10d+\sum \limits_{i=1}^d\left[{x}_i^2-10\cos \left(2\pi {x}_i\right)\right]$
f(x)20	Rosenbrock	f(x∗) = 0; x∗ = (0.5, …, 0.5)	[−100, 100]d	30	$f(x)=\sum \limits_{i=1}^d100{\left({x}_{i+1}-{x_i}^2\right)}^2+{\left({x}_i-1\right)}^2$
f(x)21	Schwefel 21	f(x∗) = 0; x∗ = (0, …, 0)	[−100, 100]d	30	f(x) =  max {|xi|, 1 ≤ i ≤ d}
f(x)22	Schwefel 22	f(x∗) = 0; x∗ = (0, …, 0)	[−100, 100]d	30	$f(x)=\sum \limits_{i=1}^d\left|{x}_i\right|+\prod \limits_{i=1}^d\left|{x}_i\right|$
f(x)23	Schwefel 26 6	f(x∗) = 0; ${\mathbf{x}}^{\ast}=\left(\begin{array}{c}420.9687,\\ {}\dots, 420.9687\end{array}\right)$	[−500, 500]d	30	$f(x)=\sum \limits_{i=1}^d\left(-{x}_i\left(\sin \left(\sqrt{\mid {x}_i\mid}\right)\right)\right)$
f(x)24	Step	f(x∗) = 0; x∗ = (0, …, 0)	[−100, 100]d	30	$f(x)=\sum \limits_{i=1}^d\mid {x}_i^2\mid$
f(x)25	Stybtang	f(x∗) =  − 39.1659n; x∗ = (−2.90, …, 2.90)	[−5, 5]d	30	$f(x)=\frac{1}{2}\sum \limits_{i=1}^d\left({x}_i^4-16{x}_i^2+5{x}_i\right)$
f(x)26	Trid	f(x∗) =  − n(n + 4)(n − 1)/6; x∗ = [i(n + 1 − i)] for i = 1, …, n	[−d2, d2]d	30	$f(x)=\sum \limits_{i=1}^d{\left({x}_i-1\right)}^2-\sum \limits_{i=2}^d{x}_i{x}_{i-1}$
f(x)27	Vincent	f(x∗) =  − n; x∗ = (7.70, …, 7.70)	[0.25, 10]d	30	$f(x)=-\frac{1}{n}\sum \limits_{i=1}^n\sin \left[10\log \left({x}_i\right)\right]$
f(x)28	Zakharov	f(x∗) = 0; x∗ = (0, …, 0)	[−5, 10]d	30	$f(x)=\sum \limits_{i=1}^d{x}_i^2+{\left(\sum \limits_{i=1}^d0.5i{x}_i\right)}^2+{\left(\sum \limits_{i=1}^d0.5i{x}_i\right)}^4$
f(x)29	Rothyp	f(x∗) = 0; x∗ = (0, …, 0)	[−65.536, 65.536]n	30	$f(x)=\sum \limits_{i=1}^d\sum \limits_{j=1}^i{x}_j^2$
f(x)30	Schwefel 2	f(x∗) = 0; x∗ = (0, …, 0)	[−100, 100]d	30	$f(x)=\sum \limits_{i=1}^d{\left(\sum \limits_{j=1}^i{x}_i\right)}^2$
f(x)31	Sphere	f(x∗) = 0; x∗ = 0, …, 0	[−5, 5]d	30	$f(x)=\sum \limits_{i=1}^d{x}_i^2$
f(x)32	Sum2	f(x∗) = 0; x∗ = (0, …, 0)	[−10, 10]d	30	$f(x)=\sum \limits_{i=1}^d{ix}_i^2$
f(x)33	Sumpow	f(x∗) = 0; x∗ = (0, …, 0)	[−1, 1]d	30	$f(x)=\sum \limits_{i=1}^d{\left|{x}_i\right|}^{i+1}$
f(x)34	Rastringin + Schwefel22 + Sphere	f(x∗) = 0; x∗ = (0, …, 0)	[−100, 100]d	30	$f(x)=\left[10d+\sum \limits_{i=1}^d\left[{x}_i^2-10\cos \left(2\pi {x}_i\right)\right]\right]+\left[\sum \limits_{i=1}^d\left|{x}_i\right|+\prod \limits_{i=1}^d\left|{x}_i\right|\right]+\left[\sum \limits_{i=1}^d{x}_i^2\right]$
f(x)35	Griewank + Rastrigin + Rosenbrock	f(x∗) = n − 1; x∗ = (0, …, 0)	[−100, 100]d	30	$f(x)=\left[\sum \limits_{i=1}^d\frac{x_i^2}{4000}-\prod \limits_{i=1}^d\cos \left(\frac{x_i}{\sqrt{i}}\right)+1\right]+\left[10d+\sum \limits_{i=1}^d\left[{x}_i^2-10\cos \left(2\pi {x}_i\right)\right]\right]+\left[\sum \limits_{i=1}^d100{\left({x}_{i+1}-{x_i}^2\right)}^2+{\left({x}_i-1\right)}^2\right]$
f(x)36	Ackley + Penalty2 + Rosenbrock + Schwefel22	f(x∗) = (1.1n) − 1; x∗ = (0, …, 0)	[−100,100]d	30	$f(x)=\left[-20\exp \left(-0.2\sqrt{\frac{1}{d}\sum \limits_{i=d}^d{x}_i^2}\right)-\exp \left(\frac{1}{d}\sum \limits_{i=1}^d\cos \left(2\pi {x}_i\right)\right)+\exp (1)+20\right]+\left[0.1\left({\left(\sin \left(3\pi {x}_1\right)\right)}^2+\sum \limits_{i=1}^{d-1}{\left({x}_i-1\right)}^2\left[1+{\mathit{\sin}}^2\left(3\pi {x}_{i+1}\right)\right]+\left[{\left({x}_i-1\right)}^2{\left(\sin \left(2\pi {x}_i\right)\right)}^2\right]\right)+\sum \limits_{i=1}^du\left({x}_i,\mathrm{5,100,4}\right)\right]+\left[\sum \limits_{i=1}^d100{\left({x}_{i+1}-{x_i}^2\right)}^2+{\left({x}_i-1\right)}^2\right]+\left[\sum \limits_{i=1}^d\left|{x}_i\right|+\prod \limits_{i=1}^d\left|{x}_i\right|\right]$
f(x)37	Ackley + Griewnk + Rastringin + Rosenbrock + Schwefel22	f(x∗) = n − 1; x∗ = (0, …, 0)	[−100,100]d	30	$f(x)=\left[-20\exp \left(-0.2\sqrt{\frac{1}{d}\sum \limits_{i=d}^d{x}_i^2}\right)-\exp \left(\frac{1}{d}\sum \limits_{i=1}^d\cos \left(2\pi {x}_i\right)\right)+\exp (1)+20\right]+\left[\sum \limits_{i=1}^d\frac{x_i^2}{4000}-\prod \limits_{i=1}^d\cos \left(\frac{x_i}{\sqrt{i}}\right)+1\right]+\left[10d+\sum \limits_{i=1}^d\left[{x}_i^2-10\cos \left(2\pi {x}_i\right)\right]\right]+\left[\sum \limits_{i=1}^d100{\left({x}_{i+1}-{x_i}^2\right)}^2+{\left({x}_i-1\right)}^2\right]+\left[\sum \limits_{i=1}^d\left|{x}_i\right|+\prod \limits_{i=1}^d\left|{x}_i\right|\right]$