Abstract
Improving long-term time series forecasting accuracy and efficiency is of great value for real-world applications. The main challenge in the long-term forecasting of multivariate time series is to accurately capture the local dynamics and long-term dependencies of time series. Currently, most approaches capture temporal dependencies and inter-variable dependencies in intertwined temporal patterns, which are unreliable. Moreover, models based on time series decomposition methods are still unable to capture both short- and long-term dependencies well. In this paper, we propose an efficient multivariate time series forecasting model CNformer with three distinctive features. (1) The CNformer is a fully CNN-based time series forecasting model. (2) In the encoder, the stacked dilated convolution as a built-in block is combined with the time series decomposition to extract the seasonal component of the time series. (3) The convolution-based encoder-decoder attention mechanism refines seasonal patterns in the decoder and captures complex combinations between different related time series. Owing to these features, our CNformer has lower memory and time overhead than models based on self-attention and the Auto-Correlation mechanism. Experimental results show that our model achieves state-of-the-art performance on four real-world datasets, with a relative performance improvement of 20.29%.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Time series forecasting has significant value in planning or decision-making in advance. How to use long sequence time series inputs to produce more accurate predictions with longer forecasting lengths has always been the goal of researchers. Traditional statistics-based forecasting methods, such as Autoregressive Integrated Moving Average (ARIMA) [1] and Exponential Smoothing (ES) models [2], are mainly univariate time series forecasting methods. These methods model each time series as a separate series. Therefore, the correlation information and common features in time series cannot be exploited, hindering the broad application of traditional methods in large-scale multivariate time series forecasting tasks. This work takes advantage of the powerful nonlinear modeling capabilities of deep learning to improve the long-term forecasting performance of multivariate time series.
The main challenge in multivariate time series forecasting is the accurate capturing of the mixed short- and long-term temporal patterns and the complex dependencies between multiple correlation series [3, 4]. In recent years, deep learning techniques have been widely applied to time series forecasting tasks with great success. The Recurrent Neural Network (RNN) [5, 6], Long Short Term Memory (LSTM) [7], and Gated Recurrent Unit (GRU) [3] are specialized sequence modeling networks. Several works have proposed time series forecasting models [5, 8] combining CNNs and RNNs to improve the ability to capture local temporal dynamics with attention mechanisms [9, 10] to capture inter-time series dependencies. The Transformer model [11] improves the ability of the model to capture long-term dependencies and allows the model to process data in parallel. The advantage of Transformer’s self-attention mechanism is its ability to capture dependencies between arbitrary time steps in a time series through point-wise dependency discovery. Several studies have integrated CNNs in Transformer-based models for computer vision [12, 13] and time series prediction [14, 15] to reduce the memory and time complexity of the canonical dot-product self-attention and make it local-aware. The sparse versions of self-attention [14,15,16] alleviate the problem of quadratic space complexity of the self-attention mechanism while improving the forecasting capability. With improved forecasting performance, these approaches still face challenges in long-term forecasting of multivariate time series.
The main problem in improving the long-term forecasting ability is that the entangled time pattern makes it extremely difficult to accurately capture time and inter-variable dependencies. First, it is unreliable to discover multiple scales of temporal patterns directly from entangled temporal patterns, especially in the case of long-term forecasts. Self-attention captures dependencies directly from mixed temporal patterns in a point-wise manner, without fully exploiting properties inherent in time series, such as seasonality and trend. Second, although some methods untangle temporal patterns to improve the accuracy of capturing temporal repeating patterns, they lack an efficient scheme for capturing temporal and inter-variate dependencies. The LSTM-MSNet [17] uses traditional time series decomposition methods for data preprocessing. However, it is difficult for LSTMs in the LSTM-MSNet to capture long-term temporal patterns. Autoformer [18] performs series-level dependency capturing by using time series decomposition and the autocorrelation mechanism, achieving state-of-the-art performance. The mathematical method-based autocorrelation mechanism is more advantageous in capturing seasonal patterns that do not change over time. However, real-world time series are a mixture of local dynamics and long-term temporal patterns. Autocorrelation fails to accurately capture the local dynamics of time series and the long-term dependencies of time series without significant periodicity. Third, existing approaches either capture inter-variable dependencies in intertwined temporal patterns [9, 10] or simply focus on unraveling temporal patterns to capture dependencies in the temporal dimension [5, 18]. Some exogenous series that are weakly correlated with the forecasting time series may impair the prediction performance [19, 20]. Therefore, effectively capturing the dependency between variables is beneficial in improving prediction performance.
From the above analysis, we conclude that in designing a time series forecasting model of better prediction accuracy, it is crucial to take the following three steps: (1) identify and refine temporal repeating patterns at multiple scales in time series; (2) decompose more predictable components from the refined time series, such as seasonal and trend-cyclical components; and (3) extract potential correlations between series and temporal repeating patterns at multiple scales. With this in mind, we propose a Transformer-based time series forecasting model using only CNNs and sequence decomposition. The contributions of this paper are summarized as follows:
-
1.
We propose the CNformer, a time series prediction model based on CNNs and sequence decomposition. The role of the CNNs is to refine and capture temporal repeating patterns and to capture complex combinations of different time series related to the target time series. The sequence decomposition block decomposes the entangled temporal patterns into more predictable, seasonal, and trend-cyclical components.
-
2.
Different from cross self-attention in Transformer, we propose encoder-decoder convolutional attention based on stacked dilated convolution. Convolutional attention captures complex combinations of different related time series and refines the seasonal patterns in the decoder using the seasonal component extracted by the encoder.
-
3.
The CNformer achieves state-of-the-art performance on four real-world multivariate time series datasets with a relative performance improvement of 20.29%. In addition, the CNformer outperforms self-attention and autocorrelation-based methods in computational and memory efficiency.
The rest of this paper is organized as follows. In Section 2, we discuss the development of time series prediction methods. Section 3 presents the proposed CNformer framework in detail. Section 4 details our experimental setup and analysis of the experimental results. Finally, Section 5 concludes this paper.
2 Related work
2.1 Time series forecasting
Due to its wide range of applications, time series forecasting has always been an area of concern for researchers, and various forecasting methods have been proposed. Traditional statistical methods are divided into linear models and nonlinear methods. Linear models mainly include ARIMA [21] and VAR [22]. The nonlinear models include the Generalized Autoregressive Conditional Heteroscedastic (GARCH) Model [23], Hidden Markov Model [24], and State Space Model [25]. In addition, machine learning methods have been widely used in the field of time series forecasting and have become a strong competitor to classical statistical models. Machine learning methods are non-parametric nonlinear data-driven forecasting models, which mainly include the Multilayer Perceptron (MLP), the Bayesian Neural Network (BNN), the Generalized Regression Neural Network (GRNN) [26], CART Regression Trees, Support Vector Regression (SVR), and Gaussian Process (GP). In [27], it is proposed to use ARIMA and MLP to capture the linear component of the time series and the nonlinear component of the error series after variational mode decomposition (VMD), respectively. However, traditional machine learning methods require complex feature engineering and have insufficient generalization capability compared to deep learning techniques, thus their limited application in high-dimensional time series prediction tasks.
Deep neural networks have recently been widely employed in time series forecasting tasks with significant performance improvements. The RNN and its variants are specialized sequence modeling neural networks [6, 17, 28,29,30]. However, RNNs have difficulty capturing the long-term dependency, a fact that [15] limits their application in time series prediction tasks, especially in the case of long sequence input and long-term prediction.
To enhance the ability of the model to capture local and long-term dependencies, a model design scheme that combines CNNs, RNNs, and attention mechanisms has achieved satisfactory results. The DA-RNN [9] uses LSTM to encode the input sequences and captures the relevant input features and long-term temporal dependencies using the input attention mechanism and the temporal attention mechanism, respectively. The LSTNet [5] uses a combination of CNNs and RNNs to extract local and long-term dependencies and introduces the recurrent-skip component to alleviate the problem that RNNs cannot capture long-term dependencies. The DSANet [31] utilizes a combination of CNN and self-attention to capture local and global dependencies. The MTNet [8] uses a large memory component to store the features of past observations encoded by CNNs and GRUs with attention mechanism to select relevant memory blocks to improve the model’s ability to capture long-term dependencies. The LSTM-MSNet [17] adopts traditional sequence decomposition for data preprocessing and feeds the multiple seasonal patterns obtained from sequence decomposition into LSTMs to improve the model’s prediction accuracy. [10] uses CNNs to extract temporal repeating patterns from the hidden states of RNNs and uses an attention mechanism to select historical information related to the hidden state of the current time step. Aiming at the problem that the attention mechanism tends to discard low-weight input vectors, the IADSN proposes the multi-dimensional attention (MA) to capture the dependencies of input vectors in the feature dimension [19]. The MDTNet [3] uses stacked dilated convolution and the GRUs to capture the complex dependencies between series and mixed short- and long-term temporal patterns. Yazici et al. [32] points out that CNNs are more efficient than the RNN and its variants in pattern extraction from sequential data and proposes a short-term electricity load prediction method using 1-D CNNs based on the video pixel network (VPN).
However, RNNs suffer from the inefficiency of the iterative generation of multi-step predictions and the insufficient ability to capture long-term temporal patterns. The Temporal Convolutional Networks (TCNs) uses dilated causal convolution to obtain a receptive field that grows exponentially with the depth of the network, enabling the model to capture long-term temporal repeating patterns. Experimental results show that the TCNs are more suitable as a starting point for sequence modeling tasks [33]. The PSTA-TCN [34] employs spatio-temporal attention and combines it with TCNs to extract dynamic temporal patterns of time series.
2.2 Transformer-based time series forecasting models
In recent years, Transformer-based [11] models have achieved great success in the fields of natural language processing [35] and computer vision [13, 36]. Recently, the Transformer architecture and self-attention mechanism have been widely used in the design of time series forecasting models with significant performance improvements.
The quadratic memory and time complexity of the canonical self-attention limits its application in long-term forecasting tasks. Several recent research efforts have been devoted to improving the efficiency of the self-attention, i.e., proposing a sparse version of the self-attention. In order to remedy the shortcomings of the self-attention, namely significant space overhead and insensitivity to the local context, [15] uses causal convolution to generate queries and keys for the self-attention layer and proposes LogSparse self-attention, where each time step of the time series only attends to itself and its previous time steps with an exponential step size. For self-attention inputs Q and K, Reformer [16] adopts Locality-Sensitive Hash (LSH) attention so that each query q only focuses on the keys in K that are closest to q. The ProbSparse self-attention [14] finds the dominant queries in Q, and each key attends only to the filtered dominant queries. In addition, Informer achieves self-attention distilling through convolution and max-pooling operations, dramatically reducing the dimension of self-attention feature maps. The tightly-coupled convolutional Transformer [37] employs self-attention distillation based on dilated convolution to enhance the model’s ability to extract dominating features. The Autoformer [18] creatively integrates the idea of sequence decomposition and the autocorrelation mechanism into the Transformer architecture. The model significantly improves the prediction performance while reducing space complexity. Unlike the point-wise dependence discovery of the self-attention, autocorrelation enables the capture of temporal repeating patterns at the sub-series level. However, the autocorrelation mechanism is unable to accurately capture dependencies across multiple scales.
The role of CNNs in existing models combining CNNs and self-attention is limited to enhancing the local perceptual ability of self-attention. In addition, the autocorrelation mechanism has insufficient ability to capture local time dynamics and cannot capture trends in time series without significant periodicity. Thus, we propose a method combining CNNs with sequence decomposition to extract more predictable seasonal and trend components. Furthermore, we propose a fully convolution-based encoder-decoder attention mechanism to extract the dependencies between time series. The experimental results show that our model outperforms the baseline models in both prediction accuracy and efficiency.
3 Methodology
3.1 Problem definition
This paper focuses on multivariate time series forecasting. Before introducing the proposed model, we first give a general definition of the multivariate time series forecasting problem. Given a historical time series input window \(\mathcal {X}=\left \{x_{1},x_{2},\cdots ,x_{T}\right \}\) of fixed length T, where \(x_{t} \in \mathbb {R}^{m}\), and m is the number of variables, the task of multivariate time series forecasting is to predict the target time series \(\mathcal {Y}=\left \{y_{T+1},y_{T+2},\cdots ,y_{T+O} \right \}\), where \(y_{t} \in \mathbb {R}^{n}\), n is the number of variables, and O is the prediction horizon. The prediction model f can be formalized as follows:
where \( \widehat {\mathcal {Y}} \in \mathbb {R}^{O \times n} \) is the time series predicted by the model, and Ω is the set of learnable parameters of the model. For time series of length L, we use the sliding window strategy [17] to transform the training data into (L-T-O) records, where T and O are the lengths of the input window and the output window, respectively. After the above transformation, the input and output window pairs are used as the training data of the CNformer.
3.2 Overview of the CNformer framework
As shown in Fig. 1, the CNformer is a multivariate time series forecasting framework with Transformer architecture. The encoder comprises three components: the stacked dilated convolutional blocks (SDCBs), sequence decomposition, and the feedforward network, which realizes the extraction of the seasonal component from the past time series. The decoder mainly plays two roles. On one hand, the decoder progressively decomposes seasonal components and trend-cyclical components from the input series; on the other hand, the convolutional attention module utilizes the historical seasonal information output by the encoder to refine the seasonal component in the decoder and extract complex combination patterns between different time series related to the forecast series.
Encoder
The role of the encoder is to refine and decompose the seasonal component. The core components of the encoder are the SDCBs and sequence decomposition components. Benefiting from the advantage of CNNs in capturing time-invariant patterns [38], SDCBs are naturally suitable for capturing and aggregating similar series-level temporal patterns. SDCBs enhance the ability to perceive local context at each time step, thus alleviating the impact of outliers on performance and potential optimization problems [15]. Furthermore, the stacked dilated convolutions in SDCBs can capture both local and long-term temporal patterns in time series, which enables the series decomposition module to obtain a refined seasonal component.
As shown in Fig. 1, the encoder consists of N encoder layers. The input time series \( \mathcal {X} \in \mathbb {R}^{L \times m} \) of length L is first transformed into \( \mathcal {X}_{en}^{0} \in \mathbb {R}^{L \times d} \) by the embedding layer, where d denotes the dimensionality of the hidden state. We use \(\mathcal {X}_{s}, \mathcal {X}_{t} = \text {SeriesDecomp}(\mathcal {X})\) to denote the time series decomposition component represented by (2). \(\mathcal {X}_{en}^{l}\) denotes the output of encoder, where \(l \in \left \{1,{\cdots } ,N\right \} \) denotes the l-th encoder layer. The detailed calculation process of the encoder is as follows:
\(\mathcal {S}^{l,i}_{en}, i \in \left \{1,2\right \} \) represents the seasonal component obtained from the i-th time series decomposition component of the l-th layer, respectively.
Decoder
The decoder extracts the trend-cyclical and seasonal components of the input time series and generates forecasts using these two more predictable components. The decoder consists of the trend-cyclical accumulation part and the seasonal pattern extraction part (one inner SDCB and one encoder-decoder SDCB). The inner SDCB module and encoder-decoder SDCB module perform convolution operations in the time and variable dimensions of the time series, respectively. The former captures and refines repeating patterns in the time dimension. The latter refines the seasonal component in the decoder using previous seasonal patterns extracted by the encoder and captures complex combinations of related time series at each time step.
The CNformer decoder consists of M decoder layers. The input of the decode consists of two parts: the seasonal part \( \mathcal {X}_{s}^{0} \in \mathbb {R}^{\left (\frac {L}{2}+O \right )\times m} \) and the trend-cyclical part \( \mathcal {T}_{de}^{0} \in \mathbb {R}^{\left (\frac {L}{2} +O \right )\times m} \). The part of length \(\frac {L}{2}\) in \(\mathcal {X}_{s}^{0}\) is the latter half of the seasonal component of encoder’s input \(\mathcal {X}_{en}\) that provides the latest seasonal information. The part of length O in \(\mathcal {X}_{s}^{0}\) are placeholders filled with zeros. The part of length \(\frac {L}{2}\) in \(\mathcal {T}_{de}^{0}\) is the second half of the trend component of of encoder’s input \(\mathcal {X}_{en}\). The part of length O in \(\mathcal {T}_{de}^{0}\) are placeholders filled with the mean of \(\mathcal {X}_{en}\). \( \mathcal {X}_{s}^{0}\) is transformed into \(\mathcal {X}_{s}^{0} \in \mathbb {R}^{\left (\frac {L}{2} +O \right )\times d}\) through the embedding layer. The detailed calculation process of the decoder is as follows:
where \(\mathcal {S}^{l,i}_{de}, \mathcal {T}^{l,i}_{de}, i \in \left \{1,2,3\right \} \) denote the seasonal and trend components obtained from the i-th time series decomposition component of the l-th layer. \(\mathcal {W}_{l} \in \mathbb {R}^{d \times m}\) denotes the matrix that projects the sum of trend components \(\mathcal {T}_{de}^{l,1}\), \(\mathcal {T}_{de}^{l,2}\) and \(\mathcal {T}_{de}^{l,3}\). \(\mathcal {X}^{M}_{de}\) is summed with \(\mathcal {T}^{M}_{de}\) after projection (\(\mathcal {X}^{M}_{de} \times \mathcal {W}_{S} + \mathcal {T}^{M}_{de} \)), and the result is used as the predicted series generated by the model. \(\mathcal {W}_{S}\) denotes the projection matrix that transforms the dimension of \(\mathcal {X}^{M}_{de}\) from d to the target dimension m.
3.3 The stacked dilated convolution blocks
In [38], the authors point out that CNNs are good at capturing time-invariant patterns in time series. The convolution module plays three roles in the CNformer. First, the convolutional component alleviates the impact of outliers on performance and potential optimization problems that may arise. Second, multi-layer convolutional networks make it possible to capture dependencies at multiple scales. Finally, convolution operations on the variable dimension of the time series can capture the inter-variable dependencies. Specifically, to obtain a more extensive effective history, we use multi-layer dilated convolutions to obtain a larger receptive field. After the convolutional component refines the input time series, the time series decomposition component obtains seasonal and trend components that are statistically more similar to the input time series.
For a single time series input \( x \in \mathbb {R}^{s}\) of length s and a filter \(f:\left \{0,\cdots ,k-1\right \}\rightarrow \mathbb {R} \) of size k, the dilated convolution operation F at time step t is defined as:
where d is the dilation factor, xt−d⋅i is the value of time series x at the \(\left (t-d \times i\right )\) time step. As shown in Fig. 2, the SDCB consists of K layers of dilated convolutional blocks. Each dilated convolutional block contains two layers of dilated convolution. Within each dilated convolution block, we set the dilation factor d = 2l for the l-th layer dilated convolution. When d = 1, the dilated convolution degenerates into a regular convolution. The exponentially increasing dilation factor allows SDCB to access the entire input time series, thus enabling the model to capture long-term temporal repeating patterns. As shown in Fig. 1, we take the SDCB as a built-in block of the CNformer. For the input time series \(\mathcal {X}_{sdcb} \in \mathbb {R}^{L \times d}\) of length L, the output of the SDCB is \( \mathcal {X}_{sdcb}^{K} \in \mathbb {R}^{L \times d}\), where K is the number of layers of the dilated convolution block. We use \(\mathcal {X}_{sdcb}^{K}=\text {SDCB}(\mathcal {X}_{sdcb})\) to summarize the calculation process of the SDCB module.
3.4 Convolutional attention mechanism
In multivariate time series forecasting tasks, it is essential to capture the complex combinations among the time series correlated with each forecast series and the short- and long-term mixed dependencies of the related time series in the time dimension [3]. Furthermore, assigning different weights to different dimensions of the encoded features improves the model’s performance [39]. The convolutional attention, an attention mechanism implemented with the SDCB module, refines the seasonal patterns in the time dimension and captures multiple complex combinations of related time series in the variable dimension. The SDBC module is referred to as the convolutional attention mechanism because it plays a similar role in the CNformer to the function of cross self-attention in the Transformer, but they are implemented differently. The self-attention captures the dependencies between time steps and is a point-wise representation aggregation method [18], while the convolutional attention performs convolution in the feature dimension of the series to capture the dependencies between variables.
The convolutional attention takes as input the concatenation of the seasonal component extracted by the encoder and the unrefined seasonal pattern in the decoder and performs convolution in the feature dimension of the input. In the time dimension, the convolutional attention utilizes the seasonal component extracted by the encoder to tune the unrefined seasonal patterns in the decoder. In the variable dimension, the convolutional attention extracts the inter-series dependencies related to the target time series. As shown in Fig. 3, the input of convolutional attention consists of two parts: the refined historical seasonal component \( \mathcal {X}_{en}^{N} \in \mathbb {R}^{L \times d}\) output by the encoder and the unrefined seasonal component \( \mathcal {X}_{de}^{l} \in \mathbb {R}^{\left (\frac {L}{2}+O \right )\times d} \) in the l-th decoder layer. First, we zero-pad \(\mathcal {X}_{en}^{N}\) to make it equal in length to \( \mathcal {X}_{de}^{l}\). Then we concatenate \( \mathcal {X}_{en}^{N}\) and \( \mathcal {X}_{de}^{l}\) in the time dimension (6) to obtain the time series \( \mathcal {X}_{en-de}^{l} \in \mathbb {R}^{(L+2O) \times d} \). Finally, the SDCB module takes \( \mathcal {X}_{en-de}^{l}\) as the input, and performs the convolution operation in the variable dimension to yield the output \( \mathcal {X}_{seasonal}^{l}\in \mathbb {R}^{\left (\frac {L}{2}+O \right )\times d}\). In the time dimension, convolutional attention achieves the fusion of \( \mathcal {X}_{en}^{N}\) and \( \mathcal {X}_{de}^{l}\), using the extracted past seasonal component \( \mathcal {X}_{en}^{N}\) to refine the seasonal patterns in \( \mathcal {X}_{de}^{l}\). We use \(\mathcal {X}_{seasonal} = \text {CovAttention}(\mathcal { X}_{en}^{N},\mathcal {X}_{de}^{l}) \) to summarize (6).
4 Experiments
We evaluate the proposed CNformer on four real-world datasets involving applications of time series forecasting in four domains: energy, transportation, economy, and disease.
4.1 Datasets
Here, we detail the four datasets used in the experiment. (1) The TrafficFootnote 1 dataset is the road occupancy on highways in the San Francisco Bay Area measured using different sensors. The dataset contains 862 time series at a time interval of 1 hour from July 2016 to July 2018. (2) The Electricity [14] dataset contains the electricity consumption (Kwh) for 320 customers, recorded every 15 minutes from July 2016 to July 2019. Since there are missing data in this dataset, Informer [14] converts this dataset into hourly electricity consumption. In this paper, we use this converted dataset. (3) The Exchange [5] dataset records the daily exchange rates for eight countries recorded from January 1990 to October 2010. (4) The ILIFootnote 2 dataset is the ratio of patients with influenza illness (ILI) to the total number of patients recorded weekly by the Centers for Disease Control and Prevention from January 2002 to June 2021. This dataset contains seven time series. We split the four datasets into training, validation, and test sets in chronological order with a ratio of 7:1:2.
4.2 Methods for comparison
We select six baseline methods to measure the performance improvement of the CNformer in multivariate time series forecasting tasks. The chosen baseline methods can be grouped into three categories: the Transformer-based models (Autoformer [18], Informer [14], and LogTrans [15]), the RNN-based models (LSTNet [5] and LSTM [7]), and the CNN-based model (TCN [33]). Autoformer innovatively integrates the sequence decomposition method into the Transformer framework and replaces the self-attention with the autocorrelation mechanism. The Informer and LogTrans models are dedicated to improving the efficiency of canonical dot-product self-attention, and both propose their respective sparse versions of self-attention: LogSparse and ProbSparse self-attention. LSTNet uses CNNs and LSTMs to capture short- and long-term temporal patterns, respectively. A variant of RNNs, LSTMs are the most basic method for time series forecasting. TCN uses deep dilated causal convolution for sequence modeling, and its large receptive field makes it competitive in capturing long-term dependencies.
4.3 Experimental settings
We use Pytorch [40] to implement the CNformer. We train the model on a NVIDIA TITAN RTX 24GB GPU with the mean square error (MSE) loss function using the ADAM [41] optimizer with an initial learning rate of 1 × 10− 4. The dimension d of hidden state in the model is 512. The batch size is 32, and all experiments are repeated three times. The CNformer contains two encoder layers and one decoder layer by default. The detailed parameters of CNformer on the four datasets are given in Table 1.
4.4 Comparisons with the state-of-the-art
We compare the performance of the CNformer with the baseline models across multiple prediction lengths on four datasets. On the datasets Traffic, Electricity and Exchange, all models have an input length of 96 and prediction lengths of 96, 192, 336 and 720. The input length on the ILI dataset is 24, and the prediction lengths are 24, 36, 48, and 60. The datasets used in the experiments can be divided into two categories: Traffic and Electricity with significant seasonality and Exchange and ILI with no seasonality or weak seasonality.
In the following, we quantify the performance improvement of the CNformer over the previous state-of-the-art results (Autoformer) using MSE as the performance metric. As shown in Table 2, the CNformer achieves state-of-the-art performance across all prediction lengths on all datasets, yielding an average MSE reduction of 20.29% compared to the Autoformer. On the Traffic dataset, CNformer achieves the most significant performance improvement (12.7%) at the prediction length 336, with an average performance improvement of 12.2% over four prediction lengths. On the Electricity dataset, when the prediction lengths are 192 and 720, the CNformer achieves 13.06% and 12.00% performance gain, respectively, and the average performance improvement over the four prediction lengths is 12.26%. Furthermore, the means of the variance of the MSE for the CNformer and the Autoformer on the four data sets are 0.11 and 0.25, respectively. This shows that the MSE of the CNformer grows steadily with increasing prediction length, indicating that the CNformer has better robustness.
Compared with the performance on the Traffic and Electricity datasets, the CNformer achieves more considerable performance gains on ILI and Exchange datasets. We also choose MSE to illustrate the performance improvement of the CNformer over the Autoformer. On the Exchange dataset, the CNformer achieves the most significant performance improvement (65%) at prediction length 720, with an average performance improvement of 40.29%. On the ILI dataset, CNformer achieves the largest performance improvement (24.33%) at prediction length 36, with an average performance improvement of 16.39%. Theses experimental results demonstrate the effectiveness of the CNformer on datasets with no significant periodicity.
4.5 Visual analysis of model predictions
In Figs. 4 and 5, we compare the predicted values generated by the CNformer and the Autoformer with the ground truth on the Electricity and Traffic datasets with significant seasonality. The series segments marked with green rectangles and orange circles are the time series’ long-term temporal patterns and local temporal dynamics, respectively. It is found that the short- and long-term time patterns captured by the CNformer match better the time patterns in the target time series than the Autoformer. This demonstrates the feasibility and superiority of our proposed method for extracting the seasonal component using a combination of stacked dilated convolutions and sequence decomposition. Furthermore, the dependencies between time series captured by the proposed convolutional attention are beneficial to improve the model’s prediction accuracy. It is also found that the Autoformer simply repeats the captured temporal patterns in the time dimension, while the CNformer can capture the local temporal dynamics in the time series while repeating the captured temporal patterns. The above findings indicate that stacked dilation convolution is capable of capturing the local time dynamics and long-term time patterns of time series. Furthermore, as can be seen in Figs. 8 and 9, compared to the Autofomer, the CNformer enjoys a closer similarity between the prediction and ground truth in terms of both the distribution and mean of the time series.
Figures 6 and 7 show the forecasting results of the CNformer and the Autoformer on the Exchange and ILI datasets without obvious periodicity. As seen in Fig. 6, at the prediction length of 720, the CNformer captures the long-term trend of the series well, while the Autoformer barely captures the long-term pattern. Since the Exchange datasets have no apparent periodicity, accurately capturing the trend component of the time series is critical to improving forecast accuracy. The Autoformer uses the Fast Fourier Transform to calculate autocorrelation, where no parameters in the model participate in the optimization process, as a result of which the model is unable to capture the long-term trend of the sequence well. In Fig. 6, the Autoformer can only capture recent trend information. As the forecast length increases, the forecast time series output by the Autoformer shows an entirely different trend from the ground truth. In Fig. 7, compared with the Autoformer, the CNformer can better capture the time series’ long-term trend and local dynamics. As can be seen in Figs. 8 and 9, the predicted time series output by the Autoformer and the ground truth exhibit significant differences in mean and distribution. This indicates that the Autoformer fails to capture the long-term dependency of time series without significant periodicity. For the CNformer, the mean values of predicted time series and ground truth are relatively consistent, indicating that the CNformer can effectively capture the trend of time series without significant periodicity. These experimental results demonstrate the effectiveness of the CNformer on datasets without apparent periodicity.
4.6 Ablation studies
We compare the performance of SDCB, Auto-Correlation, and other attention mechanisms on the Traffic and Exchange dataset. We replace the SDCB modules in the CNformer with Auto-Correlation, full-attention, and ProbSparse-attention, respectively. As shown in Table 3, the CNformer achieves the best performance for all input and output settings, verifying the effectiveness of the proposed scheme. In addition, Auto-Correlation and full-attention fail to produce prediction results due to insufficient memory at the prediction length 1440, proving that the CNformer has higher memory usage efficiency. The results in Table 4 show that CNformer effectively improves performance on datasets with no significant periodicity.
4.7 Hyperparameters analysis
The ability of the stacked dilation convolution to accurately capture the seasonal and trend components of the historical time series is critical to improving prediction performance. In addition, the number of layers of encoder and decoder in the CNformer determines whether the model can efficiently capture temporal repeating patterns at multiple scales. To this end, we experimentally analyze the impact of parameters related to the convolutional component and the number of layers of the model on performance.
It can be seen from Fig. 10 that when the kernel size of the SDBC component is 3 and the number of layers is 1, the model achieves the best performance. Since we use dilated convolutions with dilation factors that increase exponentially, the simpler convolutional network captures dependencies across multiple scales. Larger convolution kernels and layers will introduce random fluctuations in the historical time series into the model, which can significantly reduce the model’s performance. In addition, the best prediction performance is achieved when the number of layers of encoder and decoder is 2 and 1, respectively. This indicates that the convolutional component in the CNformer can capture temporal patterns efficiently.
4.8 Statistical analysis of forecasting output
This section evaluates the distribution similarity between the input time series and the predicted series generated by the CNformer and the Autoformer. For a more realistic statistical analysis, we select two types of typical time Series with significant periodicity and no apparent periodicity: Electricity and Exchange datasets. In Table 5, we use a two-tailed t-Test with the confidence level α = 0.05 to test whether the distribution of the CNformer’s predicted time series is more similar to that of the input time series.
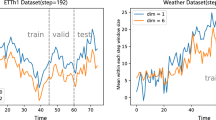
The null hypothesis of the t-Test is that the means of the two time series are the same. A p-value of t-Test greater than 0.05 indicates that the null hypothesis is accepted, suggesting that the forecast time series and the input time series have a similar distribution. When the p-value is less than 0.05, the null hypothesis is rejected. A larger p-value indicates a higher probability that the two time series have the same mean value. In addition, the larger the value of the t-statistic, the more significant the difference between the predicted time series and the true time series. The statistical analysis results in Table 5 show that the forecast time series generated by the CNformer has a more similar distribution to the input time series. For Electricity, a data set with significant periodicity, the p-values of CNformer at the prediction lengths 96 and 336 are greater than 0.05. However, the p-values of the Autoformer for both prediction lengths are less than 0.05, indicating that the difference between the mean values of the predicted sequence and the input sequence is significant. For time series with significant randomness, the task of time series forecasting becomes more complex. Although the p-value of the CNformer’s predicted sequence on the Exchange dataset is less than 0.05, the CNformer achieves better prediction results than the Autoformer does. The above results demonstrate the effectiveness of the CNformer in improving prediction performance.
4.9 Efficiency analysis
On the Electricity dataset, we experimentally compare the graph memory usage and training time of SDCB, Auto-Correlation, full attention, and ProbSparse attention. In the experiments on memory usage and training time, the input lengths of the time series are 96 and 336, respectively, and the prediction lengths are 96, 192, 348, 768, and 1536, respectively.
The experimental results are shown in Fig. 11. In terms of memory usage efficiency, the CNformer consumes the least memory across all prediction lengths. When the prediction length is 1536, the memory usage of the CNformer is 30.97% and 34.38% less than those of Auto-Correlation and ProbSparse attention, respectively. In addition, when the prediction length is 1536, the running times of CNformer, Auto-Correlation, and ProbSparse attention are relatively close, while the full attention has a significant longer running time than the other three models.
5 Conclusion
This paper focuses on the long-term multivariate time series forecasting problem. To improve the forecasting performance and efficiency, we propose the CNformer, a multivariate time series prediction model based on the Transformer architecture that combines CNNs and sequence decomposition. We use stacked dilated convolutional networks to capture and refine the seasonal patterns of time series. Furthermore, we design an attention mechanism based on stacked dilated convolution. Convolutional attention exploits historical seasonal patterns to refine the seasonal component in the time dimension and captures complex combinations of related time series in the variable dimension. Experimental results show that the CNformer not only achieves better performance than the Autoformer, but also outperforms the Autoformer in memory and computational efficiency.
References
Yamak PT, Yujian L, Gadosey PK (2019) A comparison between arima, lstm, and gru for time series forecasting. In: Proceedings of the 2019 2nd international conference on algorithms, computing and artificial intelligence, pp 49–55
Smyl S (2020) A hybrid method of exponential smoothing and recurrent neural networks for time series forecasting. Int J Forecast 36(1):75–85
Song W, Fujimura S (2021) Capturing combination patterns of long-and short-term dependencies in multivariate time series forecasting. Neurocomputing 464:72–82
Yin C, Dai Q (2022) A deep multivariate time series multistep forecasting network. Appl Intell 52(8):8956–8974
Lai G, Chang W-C, Yang Y, Liu H (2018) Modeling long-and short-term temporal patterns with deep neural networks. In: The 41st International ACM SIGIR conference on research & development in information retrieval, pp 95–104
Salinas D, Flunkert V, Gasthaus J, Januschowski T (2020) Deepar: probabilistic forecasting with autoregressive recurrent networks. Int J Forecast 36(3):1181–1191
Niu H, Xu K, Wang W (2020) A hybrid stock price index forecasting model based on variational mode decomposition and lstm network. Appl Intell 50(12):4296–4309
Chang Y-Y, Sun F-Y, Wu Y-H, Lin S-D A memory-network based solution for multivariate time-series forecasting, arXiv:1809.02105
Qin Y, Song D, Cheng H, Cheng W, Jiang G, Cottrell GW (2017) A dual-stage attention-based recurrent neural network for time series prediction. In: Proceedings of the 26th international joint conference on artificial intelligence, pp 2627–2633
Shih S-Y, Sun F-K, Lee H-y (2019) Temporal pattern attention for multivariate time series forecasting. Mach Learn 108(8):1421–1441
Vaswani A, Shazeer N, Parmar N, Uszkoreit J, Jones L, Gomez AN, Kaiser Ł, Polosukhin I (2017) Attention is all you need. In: Advances in neural information processing systems, pp 5998–6008
Wang W, Xie E, Li X, Fan D-P, Song K, Liang D, Lu T, Luo P, Shao L (2021) Pyramid vision transformer: A versatile backbone for dense prediction without convolutions. In: Proceedings of the IEEE/CVF international conference on computer vision, pp 568–578
Chu X, Tian Z, Wang Y, Zhang B, Ren H, Wei X, Xia H, Shen C (2021) Twins: Revisiting the design of spatial attention in vision transformers. Adv Neural Inf Process Syst 34:9355–9366
Zhou H, Zhang S, Peng J, Zhang S, Li J, Xiong H, Zhang W (2021) Informer: Beyond efficient transformer for long sequence time-series forecasting. In: Proceedings of AAAI
Li S, Jin X, Xuan Y, Zhou X, Chen W, Wang Y-X, Yan X (2019) Enhancing the locality and breaking the memory bottleneck of transformer on time series forecasting. Adv Neural Inf Process Syst 32:5243–5253
Kitaev N, Kaiser L, Levskaya A (2019) Reformer: the efficient transformer. In: International conference on learning representations
Bandara K, Bergmeir C, Hewamalage H (2020) Lstm-msnet: Leveraging forecasts on sets of related time series with multiple seasonal patterns. IEEE Trans Neural Netw Learn Syst 32(4):1586–1599
Wu H, Xu J, Wang J, Long M (2021) Autoformer: Decomposition transformers with auto-correlation for long-term series forecasting. Adv Neural Inf Process Syst 34:22419– 22430
He X, Shi S, Geng X, Xu L (2022) Information-aware attention dynamic synergetic network for multivariate time series long-term forecasting. Neurocomputing 500:143–154
Bi H, Lu L, Meng Y (2022) Hierarchical attention network for multivariate time series long-term forecasting. Appl Intell :1–12
Karanikola A, Liapis CM, Kotsiantis S (2022) A comparison of contemporary methods on univariate time series forecasting. In: Advances in machine learning/deep learning-based technologies, Springer, pp 143–168
Hajmohammadi H, Heydecker B (2021) Multivariate time series modelling for urban air quality. Urban Clim 37:100834
Fathian F, Fard AF, Ouarda TB, Dinpashoh Y, Nadoushani SM (2019) Modeling streamflow time series using nonlinear setar-garch models. J Hydrol 573:82–97
Zhang M, Jiang X, Fang Z, Zeng Y, Xu K (2019) High-order hidden markov model for trend prediction in financial time series. Phys A Stat Mech Appl 517:1–12
Rangapuram SS, Seeger M, Gasthaus J, Stella L, Wang Y, Januschowski T (2018) Deep state space models for time series forecasting. In: Proceedings of the 32nd international conference on neural information processing systems, pp 7796–7805
Martínez F, Charte F, Frías MP, Martínez-Rodríguez AM (2022) Strategies for time series forecasting with generalized regression neural networks. Neurocomputing 491:509–521
Chen W, Xu H, Chen Z, Jiang M (2021) A novel method for time series prediction based on error decomposition and nonlinear combination of forecasters. Neurocomputing 426:85–103
Chen Z, Ma Q, Lin Z (2021) Time-aware multi-scale rnns for time series modeling. In: IJCAI
Yang T, Yu X, Ma N, Zhao Y, Li H (2021) A novel domain adaptive deep recurrent network for multivariate time series prediction. Eng Appl Artif Intell 106:104498
Yang Y, Fan C, Xiong H (2022) A novel general-purpose hybrid model for time series forecasting. Appl Intell 52(2):2212–2223
Huang S, Wang D, Wu X, Tang A (2019) Dsanet: Dual self-attention network for multivariate time series forecasting. In: Proceedings of the 28th ACM international conference on information and knowledge management, pp 2129–2132
Yazici I, Beyca OF, Delen D (2022) Deep-learning-based short-term electricity load forecasting: A real case application. Eng Appl Artif Intell 109:104645
Bai S, Kolter JZ, Koltun V An empirical evaluation of generic convolutional and recurrent networks for sequence modeling. arXiv:1803.01271
Fan J, Zhang K, Huang Y, Zhu Y, Chen B (2021) Parallel spatio-temporal attention-based TCN for multivariate time series prediction. Neural Comput Applic :1–10
Kenton JDM-WC, Toutanova LK (2019) Bert: Pre-training of deep bidirectional transformers for language understanding. In: Proceedings of NAACL-HLT, pp 4171–4186
Liu Z, Lin Y, Cao Y, Hu H, Wei Y, Zhang Z, Lin S, Guo B (2021) Swin transformer: Hierarchical vision transformer using shifted windows. In: Proceedings of the IEEE/CVF international conference on computer vision, pp 10012–10022
Shen L, Wang Y (2022) Tcct: Tightly-coupled convolutional transformer on time series forecasting. Neurocomputing 480:131–145
Lara-benítez P, Carranza-García M, Luna-Romera JM, Riquelme JC (2020) Temporal convolutional networks applied to energy-related time series forecasting. Appl Sci 10(7):2322
Fang X, Yuan Z (2019) Performance enhancing techniques for deep learning models in time series forecasting. Eng Appl Artif Intell 85:533–542
Paszke A, Gross S, Massa F, Lerer A, Bradbury J, Chanan G, Killeen T, Lin Z, Gimelshein N, Antiga L et al (2019) Pytorch: an imperative style, high-performance deep learning library. In: Proceedings of the 33rd international conference on neural information processing systems, pp 8026–8037
Kingma DP, Ba J (2015) Adam: a method for stochastic optimization. In: International conference on learning representations
Funding
This work is partially supported by a grant from the National Natural Science Foundation of China (No. 62272368, No. 62032017), the Innovation Capability Support Program of Shaanxi (No. 2023-ZC-TD-0008), the Key Research and Development Program of Shaanxi (No. 2021ZDLGY03-09, No. 2021ZDLGY07-02, No. 2021ZDLGY07-03), Shaanxi Qinchuangyuan “scientists+engineers” team in 2023 (No. 41), and The Youth Innovation Team of Shaanxi Universities.
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Conflict of Interests
The authors have no competing financial interests to declare that are relevant to the content of this article.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Wang, X., Liu, H., Yang, Z. et al. CNformer: a convolutional transformer with decomposition for long-term multivariate time series forecasting. Appl Intell 53, 20191–20205 (2023). https://doi.org/10.1007/s10489-023-04496-6
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10489-023-04496-6