Abstract
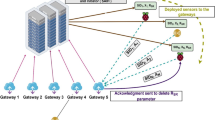
Advanced Persistent Threat (APT) attack is one of the most dangerous cyber-attack techniques nowadays. Therefore, the issue of detecting and predicting the spread of APT malware in the network is a very urgent issue to help the process of preventing this attack effectively. In this paper, we propose a new approach that is capable of predicting the spread of APT malware in the network based on the APT's own behaviors. Accordingly, to predict the spread of APT malicious code in the system, we propose to use a combination of two single Susceptible‐Infected‐Recovered (SIR) models. Specifically, the first SIR model was built to predict the spread of APT malicious code to devices and computers within the organization. These devices and computers are often used by APT malicious code as a basis to escalate privileges to devices or computers containing important and sensitive information of the organization. The second SIR model has the function of predicting the spread of APT malware to a group of computers containing sensitive information or potentially causing high risks to the organization. The two SIR models will provide information about infections between computer groups in the system to help accurately predict the spread of APT malware in the system. The proposal to combine two SIR models in the article is a new proposal based on the behavior of APT malware in practice. By combining two SIR models, the proposal in this article has opened up a new approach for a number of problems predicting the spread in the internet such as malicious code in wireless sensor networks or malicious information on the social network.















Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Data availability
The datasets generated and (or) analysed during the current study are available from the corresponding author on reasonable request.
References
Alanazi SA, Kamruzzaman MM, Alruwaili M, Alshammari N, Alqahtani SA, Karime A (2020) Measuring and Preventing COVID-19 Using the SIR Model and Machine Learning in Smart Health Care. J Healthc Eng 2020:8857346. https://doi.org/10.1155/2020/8857346
Youssef M, Scoglio C (2011) An individual-based approach to SIR epidemics in contact networks. J Theor Biol 283(1):136–144
Yang X, Yang L-X (2022) 2012 Towards the Epidemiological Modeling of Computer Viruses. Discrete Dynamics in Nature and Society 2022(259671):11. https://doi.org/10.1155/2012/259671
Prajapati A (2023) A Propagation Model of Malicious Objects via Removable Devices and Sensitivity Analysis of the Parameters. In: Abd El-Latif, A.A., Maleh, Y., Mazurczyk, W., ELAffendi, M., I. Alkanhal, M. (eds) Advances in Cybersecurity, Cybercrimes, and Smart Emerging Technologies. CCSET 2022. Engineering Cyber-Physical Systems and Critical Infrastructures, vol 4. Springer, Cham
Hosseini S, Zandvakili A (2022) The SEIRS-C model of information diffusion based on rumour spreading with fuzzy logic in social networks. Int J Comput Math 99(9):1918–1940
Yeh W-C, Lin E, Huang C-L (2021) Predicting Spread Probability of Learning-Effect Computer Virus. Complexity 2021(6672630):17. https://doi.org/10.1155/2021/6672630
Diekmann O, Heesterbeek JA, Roberts MG (2010) The construction of next-generation matrices for compartmental epidemic models. J R Soc Interface 7(47):873–885
Piqueira JR, Batistela CM (2019) Considering Quarantine in the SIRA Malware Propagation Model. Math Probl Eng 6467104:8. https://doi.org/10.1155/2019/6467104
Alshamrani A, Myneni S, Chowdhary A, Huang D (2019) A Survey on Advanced Persistent Threats: Techniques, Solutions, Challenges, and Research Opportunities. IEEE Commun Surv Tutorials 21(2):1851–1877. https://doi.org/10.1109/COMST.2019.2891891
Zhou Y, Wang Y, Zhou K, Shen S-F, Ma W-X (2023) Dynamical behaviors of an epidemic model for malware propagation in wireless sensor networks. Front Phys 11, https://doi.org/10.3389/fphy.2023.1198410.
Hosseini S, Azgomi MA (2019) Dynamical analysis of a malware propagation model considering the impacts of mobile devices and software diversification, Physica A: Statistical Mechanics and its Applications, Elsevier, vol. 526(C)
Putra DPW, Rudhito MA (2022) Solution of the SIR mathematical model with births and deaths for COVID-19 spread using microsoft excel. In Amer Inst Phys Conf Ser 2575(1). https://doi.org/10.1063/5.0108052
Rahman H, Khair A, Sultana N (2022) A Competitive Study on the Euler and Different Order Runge-Kutta Methods with Accuracy and Stability. Int J Scie Res Math Stat Sci 9(1):14–18
Ahmed N, Raza A, Rafiq M, Ahmadian A, Batool N, Salahshour S (2021) Numerical and bifurcation analysis of SIQR model. Chaos Solitons Fractals 150:111133. https://doi.org/10.1016/j.chaos.2021.111133
Simon CM (2020) The SIR dynamic model of infectious disease transmission and its analogy with chemical kinetics. PeerJ Physical Chemistry 2:e14. https://doi.org/10.7717/peerj-pchem.14
Hosseini S, Azgomi MA (2018) The dynamics of an SEIRS-QV malware propagation model in heterogeneous networks. Phys A: Stat Mech Appl 512:803–817. https://doi.org/10.1016/j.physa.2018.08.081
Zhang Z, Kumari S, Upadhyay RK (2019) A delayed e-epidemic SLBS model for computer virus. Adv Differ Equ 2019:414. https://doi.org/10.1186/s13662-019-2341-8
Wang X, Peng H, Shi B, Jiang D, Zhang S, Chen B (2019) Optimal vaccination strategy of a constrained time-varying SEIR epidemic model. Commun Nonlinear Sci Numer Simul 67:37–48. https://doi.org/10.1016/j.cnsns.2018.07.003
Gao Q, Zhuang J (2020) Stability analysis and control strategies for worm attack in mobile networks via a VEIQS propagation model. Appl Math Comput 368:124584. https://doi.org/10.1016/j.amc.2019.124584
Zheng Y, Zhu J, Lai C (2020) A SEIQR Model considering the Effects of Different Quarantined Rates on Worm Propagation in Mobile Internet. Math Prob Eng 2020(8161595):16. https://doi.org/10.1155/2020/8161595
Batista FK, Martín del Rey A, Queiruga-Dios A (2020) A New Individual-Based Model to Simulate Malware Propagation in Wireless Sensor Networks. Math 8(3):410. https://doi.org/10.3390/math8030410
Liu X, Liu J (2020) Novel non-linear dynamics P2P network worm propagation and immune model. IET Inf Security 14(2):175–184. https://doi.org/10.1049/iet-ifs.2019.0262
Fang Z, Zhao P, Xu M, Xu S, Hu T, Fang X (2020) Statistical modeling of computer malware propagation dynamics in cyberspace. J Appl Stat 49(4):858–883. https://doi.org/10.1080/02664763.2020.1845621
Dong NP, Long HV, Khastan A (2020) Optimal control of a fractional order model for granular SEIR epidemic with uncertainty. Commun Nonlinear Sci Numer Simul 88:105312. https://doi.org/10.1016/j.cnsns.2020.105312
Zhou P, Xiaojing G, Nepal S, Zhou J (2021) Modeling social worm propagation for advanced persistent threats. Comput Secur 108:102321. https://doi.org/10.1016/j.cose.2021.102321
Zhang C, Zhou P (2022) Identifying Propagation Source of Worms with Convolutional Neural Networks. 2022 IEEE 8th Int Conf Comput Commun (ICCC), Chengdu, China, pp. 1466–1470, https://doi.org/10.1109/ICCC56324.2022.10065793
Grunnill M, Arino J, McCarthy Z, Bragazzi NL, Coudeville L, Thommes EW, Amiche A, Ghasemi A, Bourouiba L, Tofighi M, Asgary A, Baky-Haskuee M, Wu J (2024) Modelling disease mitigation at mass gatherings: A case study of COVID-19 at the 2022 FIFA World Cup. PLoS Comput Biol 20(1):e1011018. https://doi.org/10.1371/journal.pcbi.1011018
Ma Y, Xu S, Luo Y, Peng J, Guo J, Dong A, Xu Z, Li J, Lei L, He L, Wang T, Yu H, Xie J (2023) Predicting the transmission dynamics of novel coronavirus infection in Shanxi province after the implementation of the “Class B infectious disease Class B management” policy. Front Public Health 11:1322430. https://doi.org/10.3389/fpubh.2023.1322430
Boëlle PY, Valdano E (2023) The importance of increasing primary vaccinations against COVID-19 in Europe. Infectious Disease Modelling 9(1):1–9. https://doi.org/10.1016/j.idm.2023.11.008
Do Xuan C, Duong D (2022) Optimization of APT Attack Detection Based on a Model Combining ATTENTION and Deep Learning. J Intell Fuzzy Syst 42(4):4135–4151
Xuan CD, Huong DT, Nguyen T (2022) A Novel Intelligent Cognitive Computing-based APT Malware Detection for Endpoint Systems. J Int Fuzzy Syst 43(3):3527–3547
Wang Y, Liu H, Li Z, Su Z, Li J Combating Advanced Persistent Threats: Challenges and Solutions. in IEEE Network, https://doi.org/10.1109/MNET.2024.3389734
Boakye-Boateng K (2024) Utilizing trust to achieve cyber resilient substations. Ph.D. dissertation, University of New Brunswick, https://unbscholar.lib.unb.ca/handle/1882/37781
Che Mat NI, Jamil N, Yusoff Y, Mat Kiah ML (2024) A systematic literature review on advanced persistent threat behaviors and its detection strategy. J Cybersecur 10(1):023. https://doi.org/10.1093/cybsec/tyad023
"APT28". MITRE ATT&CK. https://attack.mitre.org/groups/G0007. (accessed Apr. 28, 2024)
Xuan CD, Huong DT, Duong D (2022) New approach for APT malware detection on the workstation based on process profile. J Intell Fuzzy Syst 43(4):4815–4834
Acknowledgements
This work has been sponsored by the scientific research from Posts and Telecommunications Institute of Technology, Vietnam.
Funding
No funding was received for this work.
Author information
Authors and Affiliations
Contributions
Cho Do Xuan raised the idea, initialized the project and designed the experiments; Anh and Phuong carried out the experiments under the supervision of Cho Do Xuan; Both authors analyze the data and results; Cho Do Xuan wrote the paper.
Corresponding author
Ethics declarations
Ethical approval
Not applicable.
Competing interests
We wish to confirm that there are no known conflicts of interest associated with this publication and there has been no significant financial support for this work that could have influenced its outcome.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix 1: Coefficients of the formula (33)
\(\begin{array}{c}{A}_{0}=-\frac{k{\mu }^{4}}{\mu +{\gamma }_{2}}+\frac{kp{\mu }^{4}}{\mu +{\gamma }_{2}}-\frac{\alpha kp{\mu }^{4}}{\mu +\alpha {\gamma }_{2}}+{\mu }^{4}+\beta {\eta }_{2}{\mu }^{3}+{\eta }_{2}{\mu }^{3}+\alpha {\gamma }_{2}{\mu }^{3}+{\gamma }_{2}{\mu }^{3}-\frac{\beta k{\eta }_{2}{\mu }^{3}}{\mu +{\gamma }_{2}}+\frac{\beta k{\eta }_{2}p{\mu }^{3}}{\mu +{\gamma }_{2}}-\frac{\alpha k{\gamma }_{2}{\mu }^{3}}{\mu +{\gamma }_{2}}\\ +\frac{\alpha kp{\gamma }_{2}{\mu }^{3}}{\mu +{\gamma }_{2}}-\frac{\alpha k{\eta }_{2}p{\mu }^{3}}{\mu +\alpha {\gamma }_{2}}-\frac{\alpha kp{\gamma }_{2}{\mu }^{3}}{\mu +\alpha {\gamma }_{2}}+\beta {\eta }_{2}^{2}{\mu }^{2}+\alpha {\gamma }_{2}^{2}{\mu }^{2}+\alpha {\eta }_{2}{\gamma }_{2}{\mu }^{2}+\alpha \beta {\eta }_{2}{\gamma }_{2}{\mu }^{2}+\beta {\eta }_{2}{\gamma }_{2}{\mu }^{2}\\ \begin{array}{c}+{\eta }_{2}{\gamma }_{2}{\mu }^{2}-\frac{\alpha \beta k{\eta }_{2}{\gamma }_{2}{\mu }^{2}}{\mu +{\gamma }_{2}}+\frac{\alpha \beta k{\eta }_{2}p{\gamma }_{2}{\mu }^{2}}{\mu +{\gamma }_{2}}-\frac{\alpha k{\eta }_{2}p{\gamma }_{2}{\mu }^{2}}{\mu +\alpha {\gamma }_{2}}+\alpha {\eta }_{2}{\gamma }_{2}^{2}\mu +\alpha \beta {\eta }_{2}{\gamma }_{2}^{2}\mu +\alpha \beta {\eta }_{2}^{2}{\gamma }_{2}\mu \\ \begin{array}{c}+\beta {\eta }_{2}^{2}{\gamma }_{2}\mu +\alpha \beta {\eta }_{2}^{2}{\gamma }_{2}^{2}\\ {A}_{1}=4{\mu }^{3}-\frac{3k{\mu }^{3}}{\mu +{\gamma }_{2}}+\frac{3kp{\mu }^{3}}{\mu +{\gamma }_{2}}-\frac{3\alpha kp{\mu }^{3}}{\mu +\alpha {\gamma }_{2}}+3\beta {\eta }_{2}{\mu }^{2}+3{\eta }_{2}{\mu }^{2}+3\alpha {\gamma }_{2}{\mu }^{2}+3{\gamma }_{2}{\mu }^{2}-\frac{2\beta k{\eta }_{2}{\mu }^{2}}{\mu +{\gamma }_{2}}+\frac{2\beta k{\eta }_{2}p{\mu }^{2}}{\mu +{\gamma }_{2}}\\ \begin{array}{c}-\frac{2\alpha k{\gamma }_{2}{\mu }^{2}}{\mu +{\gamma }_{2}}+\frac{2\alpha kp{\gamma }_{2}{\mu }^{2}}{\mu +{\gamma }_{2}}-\frac{2\alpha k{\eta }_{2}p{\mu }^{2}}{\mu +\alpha {\gamma }_{2}}-\frac{2\alpha kp{\gamma }_{2}{\mu }^{2}}{\mu +\alpha {\gamma }_{2}}+2\alpha {\gamma }_{2}^{2}\mu +2\beta {\eta }_{2}^{2}\mu +2\alpha {\eta }_{2}{\gamma }_{2}\mu \\ +2\alpha \beta {\eta }_{2}{\gamma }_{2}\mu +2\beta {\eta }_{2}{\gamma }_{2}\mu +2{\eta }_{2}{\gamma }_{2}\mu -\frac{\alpha \beta k{\eta }_{2}{\gamma }_{2}\mu }{\mu +{\gamma }_{2}}+\frac{\alpha \beta k{\eta }_{2}p{\gamma }_{2}\mu }{\mu +{\gamma }_{2}}-\frac{\alpha k{\eta }_{2}p{\gamma }_{2}\mu }{\mu +\alpha {\gamma }_{2}}+\alpha {\eta }_{2}{\gamma }_{2}^{2}\\ \begin{array}{c}+\alpha \beta {\eta }_{2}{\gamma }_{2}^{2}+\alpha \beta {\eta }_{2}^{2}{\gamma }_{2}+\beta {\eta }_{2}^{2}{\gamma }_{2}\\ {A}_{2}=6{\mu }^{2}-\frac{3k{\mu }^{2}}{\mu +{\gamma }_{2}}+\frac{3kp{\mu }^{2}}{\mu +{\gamma }_{2}}-\frac{3\alpha kp{\mu }^{2}}{\mu +\alpha {\gamma }_{2}}+3\beta {\eta }_{2}\mu +3{\eta }_{2}\mu +3\alpha {\gamma }_{2}\mu +3{\gamma }_{2}\mu -\frac{\beta k{\eta }_{2}\mu }{\mu +{\gamma }_{2}}+\frac{\beta k{\eta }_{2}p\mu }{\mu +{\gamma }_{2}}-\frac{\alpha k{\gamma }_{2}\mu }{\mu +{\gamma }_{2}}\\ \begin{array}{c}+\frac{\alpha kp{\gamma }_{2}\mu }{\mu +{\gamma }_{2}}-\frac{\alpha k{\eta }_{2}p\mu }{\mu +\alpha {\gamma }_{2}}-\frac{\alpha kp{\gamma }_{2}\mu }{\mu +\alpha {\gamma }_{2}}+\beta {\eta }_{2}^{2}+\alpha {\gamma }_{2}^{2}+\alpha {\eta }_{2}{\gamma }_{2}+\alpha \beta {\eta }_{2}{\gamma }_{2}+\beta {\eta }_{2}{\gamma }_{2}+{\eta }_{2}{\gamma }_{2}\\ {A}_{3}=4\mu -\frac{k\mu }{\mu +{\gamma }_{2}}+\frac{kp\mu }{\mu +{\gamma }_{2}}-\frac{\alpha kp\mu }{\mu +\alpha {\gamma }_{2}}+\beta {\eta }_{2}+{\eta }_{2}+\alpha {\gamma }_{2}+{\gamma }_{2}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\)
Appendix 2: Steps to implement the RK4 method for the Advanced SIR model as follow:
-
Step 1:
$${x}_{1}^{\left(1\right)}=h\left[p\mu -\alpha k\left({I}_{1}^{n}+{I}_{2}^{n}\right){S}_{1}^{n}-\mu {S}_{1}^{n}\right]$$$${x}_{2}^{\left(1\right)}=h\left[\left(1-p\right)\mu -k\left({I}_{1}^{n}+{I}_{2}^{n}\right){S}_{2}^{n}-\mu {S}_{2}^{n}\right]$$$${y}_{1}^{\left(1\right)}=h\left[\alpha k\left({I}_{1}^{n}+{I}_{2}^{n}\right){S}_{1}^{n}-\beta {\eta }_{2}{I}_{1}^{n}-\mu {I}_{1}^{n}\right]$$$${y}_{2}^{\left(1\right)}=h\left[k\left({I}_{1}^{n}+{I}_{2}^{n}\right){S}_{2}^{n}-{\eta }_{2}{I}_{2}^{n}-\mu {I}_{2}^{n}\right]$$$${z}_{1}^{\left(1\right)}=h\left[\beta {\eta }_{2}{I}_{1}^{n}-\mu {R}_{1}^{n}\right]$$$${z}_{2}^{\left(1\right)}=h\left[{\eta }_{2}{I}_{2}^{n}-\mu {R}_{2}^{n}\right]$$ -
Step 2:
$${x}_{1}^{\left(2\right)}=h\left[p\mu -\left(\alpha k\left(\left({I}_{1}^{n}+\frac{{y}_{1}^{\left(1\right)}}{2}\right)+\left({I}_{2}^{n}+\frac{{y}_{2}^{\left(1\right)}}{2}\right)\right)+\mu \right)\left({S}_{1}^{n}+\frac{{x}_{1}^{\left(1\right)}}{2}\right)\right]$$$${x}_{2}^{\left(2\right)}=h\left[\left(1-p\right)\mu -\left(k\left(\left({I}_{1}^{n}+\frac{{y}_{1}^{\left(1\right)}}{2}\right)+\left({I}_{2}^{n}+\frac{{y}_{2}^{\left(1\right)}}{2}\right)\right)+\mu \right)\left({S}_{2}^{n}+\frac{{x}_{2}^{\left(1\right)}}{2}\right)\right]$$$${y}_{1}^{\left(2\right)}=h\left[\alpha k\left(\left({I}_{1}^{n}+\frac{{y}_{1}^{\left(1\right)}}{2}\right)+\left({I}_{2}^{n}+\frac{{y}_{2}^{\left(1\right)}}{2}\right)\right)\left({S}_{1}^{n}+\frac{{x}_{1}^{\left(1\right)}}{2}\right)-\left(\beta {\eta }_{2}+\mu \right)\left({I}_{1}^{n}+\frac{{y}_{1}^{\left(1\right)}}{2}\right)\right]$$$${y}_{2}^{\left(2\right)}=h\left[k\left(\left({I}_{1}^{n}+\frac{{y}_{1}^{\left(1\right)}}{2}\right)+\left({I}_{2}^{n}+\frac{{y}_{2}^{\left(1\right)}}{2}\right)\right)\left({S}_{2}^{n}+\frac{{x}_{2}^{\left(1\right)}}{2}\right)-\left({\eta }_{2}+\mu \right)\left({I}_{2}^{n}+\frac{{y}_{2}^{\left(1\right)}}{2}\right)\right]$$$${z}_{1}^{\left(2\right)}=h\left[\beta {\eta }_{2}\left({I}_{1}^{n}+\frac{{y}_{1}^{\left(1\right)}}{2}\right)-\mu \left({R}_{1}^{n}+\frac{{z}_{1}^{\left(1\right)}}{2}\right)\right]$$$${z}_{2}^{\left(2\right)}=h\left[{\eta }_{2}\left({I}_{2}^{n}+\frac{{y}_{2}^{\left(1\right)}}{2}\right)-\mu \left({R}_{2}^{n}+\frac{{z}_{2}^{\left(1\right)}}{2}\right)\right]$$ -
Step 3:
$${x}_{1}^{\left(3\right)}=h\left[p\mu -\left(\alpha k\left(\left({I}_{1}^{n}+\frac{{y}_{1}^{\left(2\right)}}{2}\right)+\left({I}_{2}^{n}+\frac{{y}_{2}^{\left(2\right)}}{2}\right)\right)+\mu \right)\left({S}_{1}^{n}+\frac{{x}_{1}^{\left(2\right)}}{2}\right)\right]$$$${x}_{2}^{\left(3\right)}=h\left[\left(1-p\right)\mu -\left(k\left(\left({I}_{1}^{n}+\frac{{y}_{1}^{\left(2\right)}}{2}\right)+\left({I}_{2}^{n}+\frac{{y}_{2}^{\left(2\right)}}{2}\right)\right)+\mu \right)\left({S}_{2}^{n}+\frac{{x}_{2}^{\left(2\right)}}{2}\right)\right]$$$${y}_{1}^{\left(3\right)}=h\left[\alpha k\left(\left({I}_{1}^{n}+\frac{{y}_{1}^{\left(2\right)}}{2}\right)+\left({I}_{2}^{n}+\frac{{y}_{2}^{\left(2\right)}}{2}\right)\right)\left({S}_{1}^{n}+\frac{{x}_{1}^{\left(2\right)}}{2}\right)-\left(\beta {\eta }_{2}+\mu \right)\left({I}_{1}^{n}+\frac{{y}_{1}^{\left(2\right)}}{2}\right)\right]$$$${y}_{2}^{\left(3\right)}=h\left[\left(\left({I}_{1}^{n}+\frac{{y}_{1}^{\left(2\right)}}{2}\right)+\left({I}_{2}^{n}+\frac{{y}_{2}^{\left(2\right)}}{2}\right)\right)k\left({S}_{2}^{n}+\frac{{x}_{2}^{\left(2\right)}}{2}\right)-\left({\eta }_{2}+\mu \right)\left({I}_{2}^{n}+\frac{{y}_{2}^{\left(2\right)}}{2}\right)\right]$$$${z}_{1}^{\left(3\right)}=h\left[\beta {\eta }_{2}\left({I}_{1}^{n}+\frac{{y}_{1}^{\left(2\right)}}{2}\right)-\mu \left({R}_{1}^{n}+\frac{{z}_{1}^{\left(2\right)}}{2}\right)\right]$$$${z}_{2}^{\left(3\right)}=h\left[{\eta }_{2}\left({I}_{2}^{n}+\frac{{y}_{2}^{\left(2\right)}}{2}\right)-\mu \left({R}_{2}^{n}+\frac{{z}_{2}^{\left(2\right)}}{2}\right)\right]$$ -
Step 4:
$${x}_{1}^{\left(4\right)}=h\left[p\mu -\left(\alpha k\left(\left({I}_{1}^{n}+{y}_{1}^{\left(3\right)}\right)+\left({I}_{2}^{n}+{y}_{2}^{\left(3\right)}\right)\right)+\mu \right)\left({S}_{1}^{n}+{x}_{1}^{\left(3\right)}\right)\right]$$$${x}_{2}^{\left(4\right)}=h\left[\left(1-p\right)\mu -\left(k\left(\left({I}_{1}^{n}+{y}_{1}^{\left(3\right)}\right)+\left({I}_{2}^{n}+{y}_{2}^{\left(3\right)}\right)\right)+\mu \right)\left({S}_{2}^{n}+{x}_{2}^{\left(3\right)}\right)\right]$$$${y}_{1}^{\left(4\right)}=h\left[\alpha k\left(\left({I}_{1}^{n}+{y}_{1}^{\left(3\right)}\right)+\left({I}_{2}^{n}+{y}_{2}^{\left(3\right)}\right)\right)\left({S}_{1}^{n}+{x}_{1}^{\left(3\right)}\right)-\left(\beta {\eta }_{2}+\mu \right)\left({I}_{1}^{n}+{y}_{1}^{\left(3\right)}\right)\right]$$$${y}_{2}^{\left(4\right)}=h\left[k\left(\left({I}_{1}^{n}+{y}_{1}^{\left(3\right)}\right)+\left({I}_{2}^{n}+{y}_{2}^{\left(3\right)}\right)\right)\left({S}_{2}^{n}+{x}_{2}^{\left(3\right)}\right)-\left({\eta }_{2}+\mu \right)\left({I}_{2}^{n}+{y}_{2}^{\left(3\right)}\right)\right]$$$${z}_{1}^{\left(4\right)}=h\left[\beta {\eta }_{2}\left({I}_{1}^{n}+{y}_{1}^{\left(3\right)}\right)-\mu \left({R}_{1}^{n}+{z}_{1}^{\left(3\right)}\right)\right]$$$${z}_{2}^{\left(4\right)}=h\left[{\eta }_{2}\left({I}_{2}^{n}+{y}_{2}^{\left(3\right)}\right)-\mu \left({R}_{2}^{n}+{z}_{2}^{\left(3\right)}\right)\right]$$ -
Final Step:
$$\left\{\begin{array}{l}{S}_{1}^{n+1}={S}_{1}^{n}+\frac{1}{6}\left[{x}_{1}^{\left(1\right)}+2{x}_{1}^{\left(2\right)}+2{x}_{1}^{\left(3\right)}+{x}_{1}^{\left(4\right)}\right]\\ {S}_{2}^{n+1}={S}_{2}^{n}+\frac{1}{6}\left[{x}_{2}^{\left(1\right)}+2{x}_{2}^{\left(2\right)}+2{x}_{2}^{\left(3\right)}+{x}_{2}^{\left(4\right)}\right]\\ {I}_{1}^{n+1}={I}_{1}^{n}+\frac{1}{6}\left[{y}_{1}^{\left(1\right)}+2{y}_{1}^{\left(2\right)}+2{y}_{1}^{\left(3\right)}+{y}_{1}^{\left(4\right)}\right]\\ {I}_{2}^{n+1}={I}_{2}^{n}+\frac{1}{6}\left[{y}_{2}^{\left(1\right)}+2{y}_{2}^{\left(2\right)}+2{y}_{2}^{\left(3\right)}+{y}_{2}^{\left(4\right)}\right]\\ {R}_{1}^{n+1}={R}_{1}^{n}+\frac{1}{6}\left[{z}_{1}^{\left(1\right)}+2{z}_{1}^{\left(2\right)}+2{z}_{1}^{\left(3\right)}+{z}_{1}^{\left(4\right)}\right]\\ {R}_{2}^{n+1}={R}_{2}^{n}+\frac{1}{6}\left[{z}_{2}^{\left(1\right)}+2{z}_{2}^{\left(2\right)}+2{z}_{2}^{\left(3\right)}+{z}_{2}^{\left(4\right)}\right]\end{array}\right.$$
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Do, X.C., Tran, H.A. & Nguyen, T.L.P. A novel approach for predicting the spread of APT malware in the network. Appl Intell 54, 12293–12314 (2024). https://doi.org/10.1007/s10489-024-05750-1
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10489-024-05750-1