Abstract
This paper introduces an algorithm to construct a bidirectional causal graph using an augmented graph. The algorithm decomposes the augmented graph, significantly reducing the size of the variable set required for conditional independence testing. Simultaneously, it preserves the fundamental structure of the augmented graph after decomposition, saving time and cost in constructing a global skeleton graph. Through experiments on discrete and continuous datasets, the algorithm demonstrates a clear advantage in runtime compared to traditional methods. In large-scale sparse networks, the training time is only about one-tenth of traditional methods. Additionally, the algorithm shows improvement in terms of construction error. Since the input to the algorithm is an augmented graph, this paper also discusses the impact on construction error when using both real and generated augmented graphs as input. Furthermore, the concept of markov blanket is extended to multivariate regression chain graphs, providing a method for rapidly constructing augmented graphs given certain prior knowledge.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Bayesian probabilistic graphical models (PGM) uses graphical structures to describe the relationships between multiple variables. PGM consists of nodes and edges, which can be directed, undirected or mixed. These edges provide a powerful way of representing independence, conditional independence and causal relationships between variables in many fields. Bayesian PGM has been widely applied in various fields, including machine learning, economics and biology [1].
A directed acyclic graph (DAG) is a probabilistic graphical model that only contains directed edges and has no directed cycles. This means there are no circular structures where multiple arrows point in the same direction. Each node in the causal network represents a variable, the directed edges between nodes represent the causal relationship or data generation relationship between variables. The presence of a directed edge between two variables indicates the existence of a specific causal relationship. Building a DAG from data is an important problem in causal inference.
Many scholars have made contributions regarding the construction of DAG, which are mainly divided into two directions: conditional independence test and search score. This paper discusses how to construct a causal network through the conditional independence test. Since the conditional independence test is based on three basic causal network structures of fork, chain and collider, there are cases where the direction of these edges cannot be determined. It will result in a markov equivalence class. If two DAGs on the same set of variables represent the same conditional independence between variables, they are called markov equivalent class. The markov equivalent DAGs are represented by PDAGs (partial directed acyclic graphs), where directed edges are common to each DAG and undirected edges can be oriented in one way in some DAGs and in another way in other DAGs [2]. Under the assumption of faithfulness [3], Verma and Pearl [3] first proposed the IC algorithm, which searches for separation sets from all possible variable subsets. The separation sets make two nodes independent. By exhaustively searching variables, to find all collider structures, then use the rules of directed acyclic graphs that do not produce new collider structures as much as possible to determine the directions of more edges. Finally, we can get a markov equivalent class. Spirtes P [4] proposed the PC (Peter and Clark) algorithm, which uses a complete graph as the skeleton and searches for separation sets in the neighbor sets of two nodes. Some up-to-date research studies [5,6,7] improved the PC algorithm to solve problems such as instability, confounders, nonlinear causal relationships and mixed variable processing. Geng [8] proposed a decomposition learning algorithm for network structures. In the case of prior knowledge of conditional independence between variables, it is not necessary to observe all variables at the same time. For multiple incomplete variable databases, local graphs are first learned and combined into a complete large graph. Subsequent literature [6, 7, 9] have made improvements to the decomposition learning algorithm.
In reality, causal relationships between variables are often not just single relationships, but rather involve mutual causation. This means that there may be latent variables that are not discovered, leading to many problems. For example, the markov equivalence classes constructed through conditional independence test algorithms may be inaccurate and may not satisfy the faithfulness assumption [3]. In MVR [10] (multivariate regression chain graph), bidirectional edges indicate a common unobserved variable H that causes two variables (\(X \leftarrow H \rightarrow Y\)). In fact, a chain graph has three different interpretations for bidirectional edges. The first interpretation (LWF) was introduced by Lauritzen, Wermuth and Frydenber [11, 12], which combines directed acyclic graphs and undirected graphs (UGs). The second interpretation (AMP) was introduced by Andersson, Madigan and Perlman, which also combined DAGs and UGs, but had separation criteria more similar to DAG [13]. The third interpretation, called the multivariate regression interpretation (MVR), was introduced by Cox and Wermuth [5, 14] to combine DAGs and bidirectional (covariance) graphs. Unlike the other two interpretations, bidirectional edges in MVR CGs have a strong intuitive meaning. MVR graphs are more widely applicable than DAG because they can handle unobserved variables.
Javidian [15] extends the decomposition learning algorithm to multivariate regression chain graphs (MVR CGs). The same advantages of this decomposition learning algorithms apply to a more general setting: it reduces complexity and increases the ability to compute independence tests. By using bidirectional edges, latent (hidden) variables can be represented in MVR CG. The algorithm can correctly recover any independent structure faithful to the MVR CG, greatly expanding the scope of application for factorization-based algorithms.
In this paper, we propose the MVR-Markov blanket (MMB) in MVR graphs based on DAG and propose an algorithm for building augmented graphs based on the MVR-Markov blanket. In the context of this algorithm, if we know the MMB of each node, we can easily and quickly construct an augmented graph. In addition, we propose an algorithm for learning MVR graphs using augmented graph. To verify the effectiveness of our algorithm, we compare it with PC-Like[16] and LCD4MVR [15] on randomly generated continuous data generated by MVR and discrete data generated by real graphs. Section 1 introduces the background and some academic achievements of scholars in the direction of constructing markov equivalence classes. Section 2 introduces symbols and definitions to facilitate the subsequent discussion of the paper. Section 3 introduces the main algorithm and provides a brief description of the algorithm through examples. Section 4 conducts simulation experiments to demonstrate the superiority of the algorithm empirically Section 5 discusses and summarizes the results. The algorithm is shown to be superior in the simulation experiments.
2 Symbols and definitions
In this paper, we consider causal graphs that contain unobserved variables, i.e., graphs that simultaneously contain directed edges and bidirectional edges. This section briefly introduces some important concepts and symbols, and more details can be found in references [9, 17].
Let V={\(X_1\),\(X_2\), ...,\(X_n\)} be the set of nodes. If there exists a directed edge (\(X_i\) \(\rightarrow \) \(X_j\)) from nodes \(X_i\) to \(X_j\), then \(X_i\) is called the parent node of \(X_j\), and \(X_j\) is the child node of \(X_i\). Any two adjacent nodes are connected by an edge. The set of parent nodes of vertex \(X_i\) is called pa(\(X_i\)). If there exist two vertices \(X_i\), \(X_j\) \(\in \) V, and there is a sequence from \(X_i\) to \(X_j\) such that each edge along the sequence has the same direction (\(X_1\) \(\rightarrow \) \(X_{i+1}\) \(\rightarrow \) ...\(\rightarrow \) \(X_{n+1}\), \(X_1=X_i\), \(X_{n+1}=X_j\)), then it is called a path of length n.
If there exists a directed path from \(X_i\) to \(X_j\) (\(X_i\) \(\rightarrow \) \(X_{i+1}\) \(\rightarrow \) ...\(\rightarrow \) \(X_j\)) in the graph and \(X_i\) is not an adjacent node to \(X_j\), then \(X_i\) is an ancestor of \(X_j\), \(X_j\) is a descendant of \(X_i\). The set of ancestor nodes of \(X_j\) that do not include \(X_j\) is denoted as an(\(X_j\)), and An(\(X_j\))=an(\(X_j\)) \(\cup \) \(X_i\).
DAG can be obtained by adding the direction of edges to an undirected graph. However, note that DAG do not contain directed cycles, which means there is no cycle with the same direction. In a DAG graph \(G=(V, E)\), if we remove the direction of edges, it can form an undirected graph \(G^U\). A collider refers to a node with two edges pointing to it (\(X_i\) \(\rightarrow \) \(X_j\) \(\leftarrow \) \(X_k\)). A path is d-separated by S (\(S \subseteq V\)) where all nodes on the path meet two conditions: (1) the node belongs to S but it is not a collider; (2) the node does not belong to S and none of its descendants belong to S. If two node sets A and B (\(A, B \subseteq V\)) are d-separated by S, stands for any path from set A to set B is d-separated by S.
Let \(U=(V, E)\) be an undirected graph. \(U^A=(A, E)\) is the subgraph induced by U, where \(A \subseteq V\) and E={\(\forall \) edge \( X_i-X_j \in E \mid \) \(X_i, X_j \in A\)}. if there exists a set C that separates A and B, it means that any path from set A to set B must include a node from C. If A, B and C are disjoint and satisfy (1) \(V=A \cup B \cup C\); (2) C separates A and B; (3) \(U^C\) is a complete graph, then (A, B, C) is a decomposition of V. In other words, the undirected graph U can be decomposed into two subgraphs \(U^{A \cup C}\) and \(U^{B \cup C}\). If the graph can continue to be decomposed, it is called reducible; otherwise, it is called prime. Prime blocks are called maximal irreducible components and can be obtained by decompositions.
An undirected graph is a graph where all edges are undirected. A complete undirected graph contains an edge between any two nodes. The triangulated graph [7] that every cycle of length greater than 4 has a chord. Triangulated graph can be obtained by adding edges to an undirected graph.
If a causal graph contains both bidirectional and directed edges and there is no partially directed cycle [18, 19], it is called a chain graph. If there is a sequence (\(X_1\), ...,\(X_{n+1}\)) and there exists a directed edge (\(X_i\) \(\rightarrow \) \(X_{i+1}\) or \(X_i\) \(\leftarrow \) \(X_{i+1}\)) or a bidirectional edge (\(X_i\) \(\leftrightarrow \) \(X_{i+1}\)) between the vertices in the sequence, then it is called a chain of length n. In a chain graph, a collider is a node with two edges pointing at it. To clarify, the collider node should be one of the following four structures: \(X_i \rightarrow X_k \leftarrow X_j\), \(X_i \leftrightarrow X_k \leftarrow X_j\), \(X_i \rightarrow X_k \leftrightarrow X_j\), or \(X_i \leftrightarrow X_k \leftrightarrow X_j\). Two nodes \(X_i\) and \(X_j\) are m-connecting under set Z if (1) Z does not contain any non-collider on the chain; (2) every collider on the chain is contained in Z. If there is no chain m-connecting node \(X_i\) and \(X_j\) under set Z, we say that nodes \(X_i\) and \(X_j\) are m-separated under set Z, and Z is called an m-separator. If \( A \cap B = \emptyset \) and Z is an m-separator, then any node in A is m-separated from any node in B by set Z. Two nodes \(X_i\) and \(X_j\) are collider-connected if there is a chain connecting \(X_i\) and \(X_j\) on which every nonendpoint vertex is a collider, such a chain is called a collider chain. Specifically, two adjacent nodes are also considered as collider-connected.
The MVR graph is a type of chain graph. Let \(MG=(V,E)\) be an MVR graph. The independence model resulting from applying the m-separation criterion to MG is denoted as m(MG), which is an extension of Pearl’s separation criterion to MVR graphs. The augmented graph is generated from a MVR graph by removing the direction of edges and connecting any two nodes that are collider-connected. In the augmented graph \(MG^a\) of MVR, \(X_i-X_j\) in \(MG^a\) \(\Leftrightarrow \) \(X_i\) and \(X_j\) are collider-connected in MG, the augmented graph and chain graph represent the same independence[15]. That is, \(X_i\) and \(X_j\) are independent in the undirected augmented graph, which means that \(X_i\) and \(X_j\) are m-separated in the chain graph.
In this paper, we assume that m-separations of MG can infer all independencies of a probability distribution of variables in V, called the faithfulness assumption [1]. After removing the direction of edges in the MVR graph, we can obtain the skeleton of the MVR graph. If two MVR graphs represent the same independent structure, that is, they have the same skeleton and collider, then they are referred to as Markov equivalence classes.
3 The proposed algorithm
This paper discusses the fast construction of the augmented graph from a dataset and the recovery of MVR graph from the augmented graph. Compared to the MVR graph, the augmented graph has additional edges, which are referred to as moral edges (i.e., edges between two collider-connected nodes). In fact, after determining all the moral edges, the direction of the edges can be determined through the obtained separator sets. Therefore, how to quickly identify moral edges is a crucial issue.
Theorem 1
Let \(MG^a\)=(V,\(E^a\)) be the augmented graph of an MVR graph. The edge between nodes \(X_i\) and \(X_j\) is a moral edge if and only if a complete separator set can be found in a certain prime block.
Theorem 1 proposes a fast method for finding moral edges, where we only need to search for separate sets in the prime blocks of the augmented graph and verify their edges. It greatly reduces computation time and is suitable for parallel computation. By verifying the independence between nodes, all moral edges can be found.
Theorem 2
Given the MMB of a target node \(X_i\), under the condition of MMB(\(X_i\)), \(X_i\) is independent of all nodes that do not belong to MMB(\(X_i\)).
Theorem 2 shows that in an MVR graph, MMB(\(X_i\)) contains all the nodes relevant to \(X_i\), which means that in searching for a separating set between \(X_i\) and other nodes, the condition set can be restricted to MMB(\(X_i\)). The information of MMB can be obtained through the expertise or empirical summary of experts in the field.
Similar to the markov blanket in a DAG, this paper proposes a markov blanket (MMB) structure for MVR graphs. In a DAG, the markov blanket of a target node \(X_i\) includes its child nodes, parent nodes and parents of its child nodes. Let MB(\(X_i\)) denote the markov blanket of node \(X_i\). For any node \(X_j\) (\(X_j \notin MB(X_i)\)), \(X_i\) is independent of \(X_j\) under the condition of the markov blanket of \(X_i\). MVR markov blanket (MMB) structure for MVR graphs includes the parent nodes of the target node, all the nodes that collider-connect with the target node, as well as all the collider nodes located on the collider chain.
Algorithm 1 proposes a way to quickly build the augmented graph. If the MMB of all nodes is known in advance, using algorithm 1 will greatly improve efficiency. It restricts the search set to MMB, which is obviously smaller than the full set V. This significantly reduces the number of conditional independence tests, thereby accelerating the speed of constructing the augmented graph.
However, sometimes MMB is difficult to obtain, and we can use other algorithms to generate the augmented graph. IAMB [20] is another fast method for constructing augmented graphs. It only requires verifying the conditional independence of any two variables under the conditions of other variables. S. Lauritzen [12] also discusses some other algorithms for constructing augmented graphs.
To address the challenges of constructing causal networks in high-dimensional data and the presence of unobserved variables, this article applies decomposition algorithms to MVR graphs. Algorithm 2 decomposes the augmented graph into prime blocks and then searches for possible separator sets within the prime blocks. By limiting the search set to the subgraphs, it reduces the size of the search set, which accelerates the speed of constructing the MVR graph. Then, the algorithm identifies some collider structures through the separator sets. Finally, without generating collider structure or partial directed cycles, it determines the direction of as many edges as possible.
Example 1
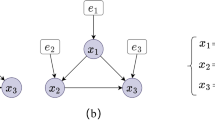
The input is an augmented graph, depicted as Fig. 1, where nodes and edges represent independent relations between variables. After step 2, the augmented graph is decomposed into four prime blocks, as shown in Fig. 2. They are subgraphs decomposed from the augmented graph. For any nodes with common neighbor nodes, such as a, f sharing a common neighbor node b, we can search for their separator sets within the subgraph containing \(\{a, f\}\). As shown in Fig. 3, we can determine whether a, f is independent under all possible subsets of \(\{b, c\}\) and add the separator sets that make them independent to the set S. We then remove the edges between a, f in the subgraph and the augmented graph. By iterating through all nodes and applying the final step of the algorithm, we can determine the directions of as many edges as possible.
Remark
Algorithm 2 is applicable to MVR graphs and DAG graphs. If the input is an undirected moral graph representing a DAG, the output will be a DAG.
4 Experimental studies
In this chapter, we conducted experiments to evaluate the performance of our algorithm on randomly generated MVR datasets and discrete datasets. We compared our algorithm with PC-LIKE [21] and LCD4MVR [15]. All algorithms are implemented in python, and data generation in R. All experiments are conducted in Windows 10 with an Intel Core i5-7th Gen with 4GB RAM. The conditional independence test is the \(\mathcal {X}^2\) test in the case of a discrete data set and the Fisher’s z-test in the case of a continuous data set. The best results are highlighted in boldface in the tables.
PC-LIKE algorithm [21]: The PC-LIKE algorithm currently applies to interpret three chain graphs, with slight variations in different stages of the algorithms. The basic ideas remain the same. In the first stage, PC-LIKE find the skeleton graph. In the second stage, the algorithm determine the direction of the edges. In the third stage, we transform the graph into a MVR graph. In references [22, 23], sequence-independent versions of the PC-LIKE algorithm were proposed for LWF, AMP and MVR CG.
LCD4MVR algorithm [15]: This algorithm was proposed by M.A.Javidian and M. Valtorta in 2020. The basic idea is to construct an MVR graph by m-separated tree. In the first step, we decompose the variable set using a separation tree. We then construct a local causal graph in the decomposed variable set and merge the global causal graph. This algorithm is an extension to the decomposition algorithm [8] with a wider range of applications. In the experiments of this paper, the PC-LIKE algorithm is adopted for the construction of local networks.
4.1 Performance evaluation metrics
-
1.
SHD: SHD is a common measurement method in constructing markov equivalence classes. The MVR graph constructed by the algorithm is mainly measured from three aspects: (1) Edges that should be added; (2) Edges that should be deleted; (3) Directions that should be changed, including deleting, inserting or adjusting the direction of edges.
-
2.
TIME: The running time of the algorithm.
In this paper, the two aspects of SHD and running time are used to measure the superiority of the algorithm. The smaller the SHD and running time, the better the calculation.
4.2 Data generation
In order to measure the performance of different algorithms on the data set, this paper adopts a data generation method similar to the paper [15]. This makes the experimental results more convincing.
Use the randDag function in the R package (pcalg) to set the number of nodes and the number of expected neighbor nodes to generate a random DAG graph, and use the AG function in the ggm package to marginalize nodes to generate an MVR graph. If the generated graph is not an MVR, repeat this step until an MVR graph is generated. The rnorm.cg function in the Lcd package can be used to generate data. N represents the amount of data, K represents the number of neighbor nodes, and V represents the total number of nodes.
\(N \in \) (3000, 10000, 30000, 50000)
\(K \in \) (3, 5)
\(V \in \) (20, 40, 60)
We need to measure the performance of algorithms under different numbers of nodes and the number of expected edges, so we set different parameters to observe the performance of the algorithm in complex networks with a large number of nodes and a high expected number of neighbor nodes, as well as in simpler networks. We generated 9 different data sets and corresponding MVR graphs.
The DAG graph can be regarded as a special case of MVR (there are no unobserved variables). In order to measure the performance of the three algorithms under the real DAG, ASIA, INSURANCE, ALARM and HAILFINDER were selected from the Bayesian Network Repository. Utilizing these four causal graphs to generate discrete data with varying data volumes.
-
1.
INSURANCE [24] with 27 vertices, 52 edges, and 984 parameters, it evaluates car insurance risks.
-
2.
ALARM [25] with 37 vertices, 46 edges and 509 parameters, it was designed by medical experts to provide an alarm message system for intensive care unit patients based on the output a number of vital signs monitoring devices.
-
3.
ASIA [26] with 8 vertices, 8 edges, and 18 parameters, it describes the diagnosis of a patient at a chest clinic who may have just come back from a trip to Asia and may be showing dyspnea.
-
4.
HAILFINDER [27] with 56 vertices, 66 edges, and 2,656 parameters. It was designed to predict severe summer hailstorms in northeastern Colorado.
In order to eliminate data inaccuracies caused by accidental factors, each algorithm was run 10 times on the data set and the final results were taken from these 10 times average.
4.3 Results
In the experiments with continuous datasets, the significance level is set at 0.005. Judging from the performance in Table 1, on the displayed continuous data set, as the amount of data increases, the running time of three algorithms increases significantly and the complexity of the causal graph (such as more nodes, more neighbor nodes) will also cause a significant drop in running speed. When the network is relatively simple, LCD4MVR is slightly better than two other algorithms. For complex networks, FLM still has the advantage in speed, but the gap between LCD4MVR and PC-LIKE is not big. Generally speaking, the running speed of LCD4MVR is slightly better than the PC-LIKE algorithm, and the FLM algorithm performs best in terms of running speed. In addition, in such a network with many nodes but few neighbor nodes, the advantages of the FLM is more obvious. In other words, FLM has greater advantages when the underlying graph is sparse.
Table 2 shows the construction error of the three algorithms on different continuous datasets. It can be seen that for sparse networks, the FLM algorithm significantly outperforms the other two algorithms, reducing the construction error by approximately twenty percent. For dense networks (i.e., networks with a higher number of neighbor nodes), FLM still achieves a more accurate MVR network, but its advantage is somewhat reduced. For small-scale networks (V=20, K=3), the SHD of FLM and LCD4MVR are basically the same, but both are better than the PC-LIKE algorithm. Under other network conditions, FLM exhibits a more significant leading advantage. As the networks become more complex, the construction errors of the three algorithms increase to some extent, which is a reasonable trend. However, when the amount of data increases, the change in SHD is not significant, and in some networks, it even increases to a certain degree. This is because when the network structure becomes complex, the relationships between variables become intricate. During the previous data generation process, certain random factors were added, resulting in relatively noisy data. When conducting conditional independence tests on variables, it is possible to obtain incorrect results. Since many variables in the network often have causal relationships, this can lead to a larger error for the entire network.
From the above discussion, it can be seen that under various network sizes, the FLM algorithm has smaller errors and performs better for networks with a larger number of nodes but fewer neighbor nodes. In terms of runtime, FLM significantly outperforms the other two algorithms, with its runtime in some networks being only one-tenth of that of the other two algorithms.
Since the input of the FLM algorithm is an augmented graph, to validate the impact of different inputs on the FLM algorithm, Fig. 4 demonstrates the construction error of the algorithm when using real augmented graphs and augmented graphs generated by IAMB. Across various causal graphs and datasets, the FLM algorithm achieves improved accuracy when it takes real augmented graphs as input, and this enhancement is even more significant in complex networks. Furthermore, due to the input of real graphs, the algorithm becomes more stable, resulting in a reduction of the construction error as the sample size increases.
Tables 3, 4, and 5 show the performance of algorithms on different discrete data sets. In these causal graphs, the real moral graph is used as the initial graph for decomposition, and different alphas (0.05, 0.01, 0.001) are selected to see the performance of the three algorithms at different significance levels. Chi-square was used for the independence test in following experiments.
Table 3 presents the performance of three algorithms on the synthetically generated ASIA dataset. In terms of SHD, all three algorithms show good performance with relatively small errors. As the amount of data increases, the errors decrease to a certain extent, and all three algorithms tend to stabilize. Overall, the FLM algorithm performs the best, achieving zero errors on datasets with sample sizes of 30000 and 50000. From the perspective of runtime, since ASIA is a relatively simple causal network, all algorithms have fast execution speeds. Among the different datasets, FLM has the shortest runtime.
As seen in Table 4, the PC-LIKE algorithm shows better performance in terms of SHD. When the sample size increases to 30000, the error basically stabilizes. For different significance levels, all algorithms construct causal relationships with minor errors, indicating that they are not sensitive to the value of alpha. In terms of runtime, the FLM algorithm exhibits a significant improvement compared to the other two. Under various datasets, there is a significant difference between LCD4MVR and PC-LIKE, which is attributed to the decomposition algorithm that reduces the search space of separating sets, greatly improving the algorithm speed. Overall, the FLM algorithm achieves the fastest speed on the ALARM dataset, and it outperforms PC-LIKE by a significant margin. In terms of error, the PC-LIKE algorithm performs the best.
Table 5 demonstrates the performance of different algorithms on the INSURANCE dataset. When the sample size is small (less than 10,000), the causal network constructed by FLM has the smallest error. However, when the sample size is large (greater than 10,000), the output of the PC-LIKE algorithm is closest to the true graph. These results suggest that increasing the sample size favors the PC-LIKE algorithm. In terms of runtime, FLM has a significant advantage due to its fewer conditional independence tests, with a runtime approximately one-quarter of LCD4MVR and one-tenth of PC-LIKE.
Compared to the other three datasets, HAILFINDER represents a larger-scale causal network. Table 6 shows the results of different algorithms on the HAILFINDER dataset. It is evident that FLM significantly outperforms the other two algorithms in both SHD and runtime metrics, and this advantage becomes even more apparent as the data size increases.
Based on the above discussion, it can be concluded that FLM exhibits significantly faster runtime compared to the other two algorithms across various sizes of discrete datasets. Additionally, it demonstrates a marked reduction in construction errors when faced with sparse networks.
5 Conclusion
In this paper, we propose an algorithm for quickly constructing MVR graphs. This algorithm starts from the augmented graph and constructs the MVR graph. It uses the idea of divide and conquer to decompose the augmented graph into prime blocks and test the conditional independence from the prime blocks. Doing so will undoubtedly speed up the construction of MVR graphs. In order to prove the advantages of the algorithm, we compared it with the PC-LIKE and LCD4MVR algorithms, respectively testing the construction of causal graphs on simulated continuous data sets and discrete data sets of real graphs. The results show that the FLM algorithm has obvious advantages in terms of running time and SHD. The effect will be better in a sparse network.
Although the advantages of the FLM algorithm have been proven through experiments, it can be seen that under complex networks, FLM’s performance in SHD is not as good as expected, which means that FLM’s recognition error rate is higher. Later research can focus on improving the performance of this algorithm on complex data sets
Availability of data and materials
The datasets analyzed in this article are available in the benchmark Bayesian network and UCI repository, https://archive.ics.uci.edu/ml/index.php, https://pages.mtu.edu/~lebrown/supplements/mmhc_paper/mmhc_index.html. Also, the datasets are available from the First and Corresponding authors’ on request.
References
Borsboom D, Deserno MK, Rhemtulla M, Epskamp S, Fried EI, McNally RJ, Robinaugh DJ, Perugini M, Dalege J, Costantini G et al (2021) Network analysis of multivariate data in psychological science. Nat Rev Methods Prim 1(1):58
Wu Q, Wang H, Lu S (2024) Nonlinear directed acyclic graph estimation based on the kernel partial correlation coefficient. Inf Sci 654:119814
Verma TS, Pearl J (2022) Equivalence and synthesis of causal models. In: Probabilistic and Causal Inference: The Works of Judea Pearl, pp 221–236
Spirtes P, Glymour C (1991) An algorithm for fast recovery of sparse causal graphs. Soc Sci Comput Rev 9(1):62–72
Wermuth N, Cox D (1993) Linear dependencies represented by chain graphs. Stat Sci 8(3):204–218
Xie X, Geng Z (2008) A recursive method for structural learning of directed acyclic graphs. J Mach Learn Res 9:459–483
Liu B, Guo J, Jing B-Y (2010) A note on minimal d-separation trees for structural learning. Artif Intell 174(5–6):442–448
Geng Z, Wang C, Zhao Q (2005) Decomposition of search for v-structures in dags. J Multivar Anal 96(2):282–294
Xie X, Geng Z, Zhao Q (2006) Decomposition of structural learning about directed acyclic graphs. Artif Intell 170(4–5):422–439
Franco VR, Barros G, Wiberg M, Laros JA (2022) Chain graph reduction into power chain graphs. Quant Comput Methods Behav Sci 2(1)
Frydenberg M (1990) The chain graph markov property. Scand J Stat 333–353
Lauritzen SL, Wermuth N (1989) Graphical models for associations between variables, some of which are qualitative and some quantitative. Ann Stat 31–57
Yang S, Cao F, Yu K, Liang J (2023) Learning causal chain graph structure via alternate learning and double pruning. IEEE Trans Big Data
Cox DR, Wermuth N (2014) Multivariate Dependencies: Models, Analysis and Interpretation vol 67. CRC Press, ???
Javidian MA, Valtorta M (2021) A decomposition-based algorithm for learning the structure of multivariate regression chain graphs. Int J Approximate Reasoning 136:66–85
Sonntag D, Peña JM (2012) Learning multivariate regression chain graphs under faithfulness. In: Sixth European Workshop on Probabilistic Graphical Models (PGM 2012), 19-21 September 2012, Granada, Spain, pp 299–306
Pearl J (1988) Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference. Morgan kaufmann, ???
Evans RJ, Richardson TS (2014) Markovian acyclic directed mixed graphs for discrete data
Richardson T (2003) Markov properties for acyclic directed mixed graphs. Scand J Stat 30(1):145–157
Asghari S, Nematzadeh H, Akbari E, Motameni H (2023) Mutual information-based filter hybrid feature selection method for medical datasets using feature clustering. Multimed Tools Appl 82(27):42617–42639
Javidian MA, Valtorta M, Jamshidi P (2019) Order-independent structure learning of multivariate regression chain graphs. In: Scalable Uncertainty Management: 13th International Conference, SUM 2019, Compiègne, France, December 16–18, 2019, Proceedings 13, pp 324–338. Springer
Javidian MA, Valtorta M, Jamshidi P (2021) An order-independent algorithm for learning chain graphs. In: The International FLAIRS Conference Proceedings, vol 34
Javidian MA, Valtorta M, Jamshidi P (2020) Amp chain graphs: Minimal separators and structure learning algorithms. J Artif Intell Res 69:419–470
Binder J, Koller D, Russell S, Kanazawa K (1997) Adaptive probabilistic networks with hidden variables. Mach Learn 29:213–244
Beinlich IA, Suermondt HJ, Chavez RM, Cooper GF (1989) The alarm monitoring system: A case study with two probabilistic inference techniques for belief networks. In: AIME 89: Second European Conference on Artificial Intelligence in Medicine, London, August 29th–31st 1989. Proceedings, pp 247–256. Springer
Lauritzen SL, Spiegelhalter DJ (1988) Local computations with probabilities on graphical structures and their application to expert systems. J Roy Stat Soc: Ser B (Methodol) 50(2):157–194
Abramson B, Brown J, Edwards W, Murphy A, Winkler RL (1996) Hailfinder: A bayesian system for forecasting severe weather. Int J Forecast 12(1):57–71
Xu P-F, Guo J, Tang M-L (2011) Structural learning for bayesian networks by testing complete separators in prime blocks. Comput Stat Data Anal 55(12):3135–3147
Lauritzen SL (1996) Graphical Models vol 17. Clarendon Press, ???
Funding
No funds, grants, or other support was received.
Author information
Authors and Affiliations
Contributions
Mingxuan Rao: Conceptualization, Methodology, Data curation, Formal analysis, Visualization, Writing- original draft. Shu Lv: Supervision, Writing - review and editing. Kaibo Shi: Writing - review and editing.
Corresponding author
Ethics declarations
Ethics approval
Written informed consent for publication of this paper was obtained from the University of Electronic Science and Technology of China and all authors.
Competing interests
The authors have no competing interests to declare that are relevant to the content of this article.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A Summary of notations
Appendix B Proofs of theorems
Proof of Theorem 1
We give the definition and some properties of bridged path sets. In an undirected graph \(G = (V,E)\), the length of a non-trivial path is greater than two. P(u, v) represents all non-trivial paths from u to v. We call a path set \(P_{uv} \subseteq P(u,v)\) bridged (on the side of v) if there exists a complete subset S (\(\subseteq ne(v,G) \)) such that p has an inner node in S for every path \( p \subseteq P_{uv}\). The set S is called a bridge of \(P_{uv}\). A more detailed definition can be found in [8].\(\square \)
Proposition 1
[28] Suppose that an undirected graph G can be decomposed into two subgraphs \(G_1\) and \(G_2\) with \(u, v \in V(G_1)\). For any bridged path set \(P_{uv}\) in G, there exists i = 1 or 2 such that \(P_{uv}(G_i)\) is also bridged in \(G_i\).
Proposition 2
[28] Let u, v be in some prime block of an undirected graph G. For any bridged path set \(P_{uv}\) in G, there exists a prime block \(U \in \mathcal {U}(G)\) such that \(P_{uv}(G_U)\) is also bridged in \(G_U\).
Lemma 1
[29] Let A, B and S be disjoint subsets of a MVR MG. Then, \(A \perp B \mid S[MG]\) if and only if S separates A from B in \((G_{An(A \cup B \cup S)})^m\).
Proposition 3
Suppose that \(u \notin pa(v)\) and \(v \notin an(u)\) in a MVR MG. Then, the set of all the paths from u to v in \(G_{An\{u,v\}}^a\) is bridged on the side of v in \(MG^a\).
Proof
It is evident that all paths from u to v are non-trivial. In graph \(MG_{An\{u,v\}}^a\), the last edge of every path from u to v corresponds to a directed edge pointing to v in MG. If this were not the case, there must exist a collider point w on such a path (because v is not an ancestor node of u, so such a w is bound to exist). However, \(w \notin pa(v)\) and \(w \notin an(u)\), so \( w \notin An\{u,v\}\). This contradicts our assumption that the path exists in \(G_{An\{u,v\}}^a\) \(\square \)
Now we are ready to prove Theorem 1. The necessity of this theorem is self-evident, now let’s proceed with the proof of sufficiency.
Assuming that (u, v) is a moral edge, it follows that (u, v) does not belong to the set of MG edges (after removing directions), \(u \notin pa(v)\) and \( \notin an(u)\). According to Lemmas proposition 4 and 5, there exits a prime block P that any path from u to v in the \(G_{An\{u,v\}}^a\) is bridged on the side of v in P, let S be the bridge and \(S \subseteq NE(v,P)\). Based on Lemma 1, u and v are independent conditional on S.
Proof of Theorem 2
Assuming there is a node v with the following three scenarios:
-
1.
If v only has paths without colliders leading to u, then the parent node w (or child node) of u must be on that path and w belongs to MMB(u). Given MMB(u) as a condition, u and v are independent.
-
2.
If all paths from v to u contain colliders, then MMB(u) will certainly include the non-collider nodes on those paths, the flow of information on this path can be blocked under the condition of MMB(u).
-
3.
A mixture of the first two scenarios. In summary, under the condition of MMB(u), u is independent of any v that does not belong to MMB(u). The theorem is thus proven.\(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Rao, M., Lv, S. & Shi, K. Learning the structure of multivariate regression chain graphs by testing complete separators in prime blocks. Appl Intell 54, 10596–10607 (2024). https://doi.org/10.1007/s10489-024-05752-z
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10489-024-05752-z