Skip to main content
Springer Nature Link
Log in

Multi-view deep subspace clustering via level-by-level guided multi-level features learning

  • Published:
Applied Intelligence Aims and scope Submit manuscript

Abstract

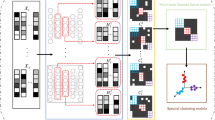
Multi-view subspace clustering has attracted extensive attention due to its ability to efficiently handle data from diverse sources. In recent years, plentiful multi-view subspace clustering methods have emerged and achieved satisfactory clustering performance. However, these methods rarely consider simultaneously handling data with a nonlinear structure and exploiting the structural and multi-level information inherent in the data. To remedy these shortcomings, we propose the novel multi-view deep subspace clustering via level-by-level guided multi-level features learning (MDSC-LGMFL). Specifically, an autoencoder is used for each view to extract the view-specific multi-level features, and multiple self-representation layers are introduced into the autoencoder to learn the subspace representations corresponding to the multi-level features. These self-representation layers not only provide multiple information flow paths through the autoencoder but also enforce multiple encoder layers to produce the multi-level features that satisfy the linear subspace assumption. With the novel level-by-level guidance strategy, the last-level feature is guaranteed to encode the structural information from the view and the previous-level features. Naturally, the subspace representation of the last-level feature can more reliably reflect the data affinity relationship and thus can be viewed as the new, better representation of the view. Furthermore, to guarantee the structural consistency among different views, instead of simply learning the common subspace structure by enforcing it to be close to different view-specific new, better representations, we conduct self-representation on these new, better representations to learn the common subspace structure, which can be applied to the spectral clustering algorithm to achieve the final clustering results. Numerous experiments on six widely used benchmark datasets show the superiority of the proposed method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Algorithm 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

Data Availability

Data will be made available on reasonable request.

Notes

  1. http://research.microsoft.com/en-us/projects/objectclassrecognition/

  2. http://cvc.cs.yale.edu/cvc/projects/yalefacesB/yalefacesB.html

  3. http://www.cs.columbia.edu/CAVE/software/softlib/

  4. https://archive.ics.uci.edu/dataset/241/one+hundred+plant+species+leaves+data+set

  5. http://archive.ics.uci.edu/ml/datasets/Multiple+Features

  6. https://data.caltech.edu/records/mzrjq-6wc02

References

  1. Peng X, Feng J, Xiao S, Yau W-Y, Zhou JT, Yang S (2018) Structured autoencoders for subspace clustering. IEEE Trans Image Process 27(10):5076–5086. https://doi.org/10.1109/TIP.2018.2848470

    Article  MathSciNet  Google Scholar 

  2. Rao S, Tron R, Vidal R, Ma Y (2010) Motion segmentation in the presence of outlying, incomplete, or corrupted trajectories. IEEE Trans Pattern Anal Mach Intell 32(10):1832–1845. https://doi.org/10.1109/TPAMI.2009.191

    Article  Google Scholar 

  3. Bazan JG (2008) Hierarchical classifiers for complex spatio-temporal concepts. Transactions on rough sets IX, 474–750. https://doi.org/10.1007/978-3-540-89876-4_26

  4. Liu G, Lin Z, Yan S, Sun J, Yu Y, Ma Y (2013) Robust recovery of subspace structures by low-rank representation. IEEE Trans Pattern Anal Mach Intell 35(1):171–184. https://doi.org/10.1109/TPAMI.2012.88

    Article  Google Scholar 

  5. Elhamifar E, Vidal R (2013) Sparse subspace clustering: Algorithm, theory, and applications. IEEE Trans Pattern Anal Mach Intell 35(11):2765–2781. https://doi.org/10.1109/TPAMI.2013.57

    Article  Google Scholar 

  6. Lu C-Y, Min H, Zhao Z-Q, Zhu L, Huang D-S, Yan S (2012) Robust and efficient subspace segmentation via least squares regression. In: Computer vision – ECCV 2012, pp 347–360. https://doi.org/10.1007/978-3-642-33786-4_26

  7. Zhang C, Hu Q, Fu H, Zhu P, Cao X (2017) Latent multi-view subspace clustering. In: 2017 IEEE conference on Computer Vision and Pattern Recognition (CVPR), pp 4333–4341. https://doi.org/10.1109/CVPR.2017.461

  8. Zhang P, Liu X, Xiong J, Zhou S, Zhao W, Zhu E, Cai Z (2022) Consensus one-step multi-view subspace clustering. IEEE Trans Knowl Data Eng 34(10):4676–4689. https://doi.org/10.1109/TKDE.2020.3045770

    Article  Google Scholar 

  9. Cai X, Huang D, Zhang G-Y, Wang C-D (2023) Seeking commonness and inconsistencies: a jointly smoothed approach to multi-view subspace clustering. Inf Fusion 91:364–375. https://doi.org/10.1016/j.inffus.2022.10.020

    Article  Google Scholar 

  10. Luo S, Zhang C, Zhang W, Cao X (2018) Consistent and specific multi-view subspace clustering. In: Thirty-second AAAI conference on artificial intelligence (AAAI), pp 3730–3737. https://doi.org/10.1609/aaai.v32i1.11617

  11. Kang Z, Zhao X, Peng C, Zhu H, Zhou JT, Peng X, Chen W, Xu Z (2020) Partition level multiview subspace clustering. Neural Netw 122:279–288. https://doi.org/10.1016/j.neunet.2019.10.010

  12. Zheng Q, Zhu J, Ma Y, Li Z, Tian Z (2021) Multi-view subspace clustering networks with local and global graph information. Neurocomputing 449:15–23. https://doi.org/10.1016/j.neucom.2021.03.115

    Article  Google Scholar 

  13. Li R, Zhang C, Fu H, Peng X, Zhou JT, Hu Q (2019) Reciprocal multi-layer subspace learning for multi-view clustering. In: 2019 IEEE/CVF International Conference on Computer Vision (ICCV), pp 8171–8179. https://doi.org/10.1109/ICCV.2019.00826

  14. Wang Q, Cheng J, Gao Q, Zhao G, Jiao L (2021) Deep multi-view subspace clustering with unified and discriminative learning. IEEE Trans Multimedia 23:3483–3493. https://doi.org/10.1109/TMM.2020.3025666

    Article  Google Scholar 

  15. Abavisani M, Patel VM (2018) Deep multimodal subspace clustering networks. IEEE J Sel Top Signal Process 12(6):1601–1614. https://doi.org/10.1109/JSTSP.2018.2875385

    Article  Google Scholar 

  16. Chen H, Wang W, Feng X (2018) Structured sparse subspace clustering with within-cluster grouping. Pattern Recogn 83:107–118. https://doi.org/10.1016/j.patcog.2018.05.020

    Article  Google Scholar 

  17. Hu H, Lin Z, Feng J, Zhou J (2014) Smooth representation clustering. In: 2014 IEEE Conference on computer vision and pattern recognition, pp 3834–3841. https://doi.org/10.1109/CVPR.2014.484

  18. Li C-G, You C, Vidal R (2017) Structured sparse subspace clustering: A joint affinity learning and subspace clustering framework. IEEE Trans Image Process 26(6):2988–3001. https://doi.org/10.1109/TIP.2017.2691557

    Article  MathSciNet  Google Scholar 

  19. Ji P, Zhang T, Li H, Salzmann M, Reid I (2017) Deep subspace clustering networks. In: Proceedings of the 31st international conference on Neural Information Processing Systems (NIPS), pp 23–32

  20. Kheirandishfard M, Zohrizadeh F, Kamangar F (2020) Multi-level representation learning for deep subspace clustering. In: 2020 IEEE Winter Conference on Applications of Computer Vision (WACV), pp 2028–2037. https://doi.org/10.1109/WACV45572.2020.9093277

  21. Dang Z, Deng C, Yang X, Huang H (2020) Multi-scale fusion subspace clustering using similarity constraint. In: 2020 IEEE/CVF conference on Computer Vision and Pattern Recognition (CVPR), pp 6657–6666. https://doi.org/10.1109/CVPR42600.2020.00669

  22. Zhang J, Li C-G, You C, Qi X, Zhang H, Guo J, Lin Z (2019) Self-supervised convolutional subspace clustering network. In: 2019 IEEE/CVF conference on Computer Vision and Pattern Recognition (CVPR), pp 5468–5477. https://doi.org/10.1109/CVPR.2019.00562

  23. Tang K, Xu K, Su Z, Jiang W, Luo X, Sun X (2019) Structure-constrained feature extraction by autoencoders for subspace clustering. In: 2019 IEEE/CVF International Conference on Computer Vision Workshop (ICCVW), pp 624–632. https://doi.org/10.1109/ICCVW.2019.00076

  24. Zhou P, Hou Y, Feng J (2018) Deep adversarial subspace clustering. In: 2018 IEEE/CVF Conference on computer vision and pattern recognition, pp 1596–1604. https://doi.org/10.1109/CVPR.2018.00172

  25. Peng X, Feng J, Zhou JT, Lei Y, Yan S (2020) Deep subspace clustering. IEEE Trans Neural Netw Learn Syst 31(12):5509–5521. https://doi.org/10.1109/TNNLS.2020.2968848

    Article  MathSciNet  Google Scholar 

  26. Peng X, Xiao S, Feng J, Yau W-Y, Yi Z (2016) Deep subspace clustering with sparsity prior. In: Proceedings of the twenty-fifth international joint conference on artificial intelligence, pp 1925–1931

  27. Chen M, Huang L, Wang C, Huang D (2020) Multi-view clustering in latent embedding space. In: Proceedings of the AAAI conference on artificial intelligence (AAAI), vol 34, pp 3513–3520. https://doi.org/10.1609/aaai.v34i04.5756

  28. Chen M-S, Huang L, Wang C-D, Huang D, Lai J-H (2021) Relaxed multi-view clustering in latent embedding space. Inf Fusion 68:8–21. https://doi.org/10.1016/j.inffus.2020.10.013

    Article  Google Scholar 

  29. Zhao J-B, Lu G-F (2022) Clean and robust affinity matrix learning for multi-view clustering. Appl Intell 52(14):15899–15915. https://doi.org/10.1007/s10489-021-03146-z

    Article  Google Scholar 

  30. Zhou T, Zhang C, Peng X, Bhaskar H, Yang J (2020) Dual shared-specific multiview subspace clustering. IEEE Trans Cybern 50(8):3517–3530. https://doi.org/10.1109/TCYB.2019.2918495

    Article  Google Scholar 

  31. Zheng Q, Zhu J, Li Z, Pang S, Wang J, Li Y (2020) Feature concatenation multi-view subspace clustering. Neurocomputing 379:89–102. https://doi.org/10.1016/j.neucom.2019.10.074

    Article  Google Scholar 

  32. Wang S, Wang Y, Lu G, Le W (2023) Mixed structure low-rank representation for multi-view subspace clustering. Appl Intell 53(15):18470–18487. https://doi.org/10.1007/s10489-023-04474-y

    Article  Google Scholar 

  33. Cao X, Zhang C, Fu H, Liu S, Zhang H (2015) Diversity-induced multi-view subspace clustering. In: 2015 IEEE conference on Computer Vision and Pattern Recognition (CVPR), pp 586–594. https://doi.org/10.1109/CVPR.2015.7298657

  34. Zhao N, Bu J (2022) Robust multi-view subspace clustering based on consensus representation and orthogonal diversity. Neural Netw 150:102–111. https://doi.org/10.1016/j.neunet.2022.03.009

    Article  Google Scholar 

  35. Si X, Yin Q, Zhao X, Yao L (2022) Consistent and diverse multi-view subspace clustering with structure constraint. Pattern Recogn 121:108196. https://doi.org/10.1016/j.patcog.2021.108196

    Article  Google Scholar 

  36. Zhang G-Y, Huang D, Wang C-D (2023) Facilitated low-rank multi-view subspace clustering. Knowl-Based Syst 260:110141. https://doi.org/10.1016/j.knosys.2022.110141

    Article  Google Scholar 

  37. Chen J, Yang S, Mao H, Fahy C (2022) Multiview subspace clustering using low-rank representation. IEEE Trans Cybern 52(11):12364–12378. https://doi.org/10.1109/TCYB.2021.3087114

    Article  Google Scholar 

  38. Wang S, Chen Y, Yi S, Chao G (2022) Frobenius norm-regularized robust graph learning for multi-view subspace clustering. Appl Intell 52(13):14935–14948. https://doi.org/10.1007/s10489-022-03816-6

    Article  Google Scholar 

  39. Zheng Q, Zhu J, Tian Z, Li Z, Pang S, Jia X (2020) Constrained bilinear factorization multi-view subspace clustering. Knowl-Based Syst 194:105514. https://doi.org/10.1016/j.knosys.2020.105514

    Article  Google Scholar 

  40. Liu X, Pan G, Xie M (2021) Multi-view subspace clustering with adaptive locally consistent graph regularization. Neural Comput Appl 33(22):15397–15412. https://doi.org/10.1007/s00521-021-06166-5

    Article  Google Scholar 

  41. Gao H, Nie F, Li X, Huang H (2015) Multi-view subspace clustering. In: 2015 IEEE International Conference on Computer Vision (ICCV), pp 4238–4246. https://doi.org/10.1109/ICCV.2015.482

  42. Wang X, Guo X, Lei Z, Zhang C, Li SZ (2017) Exclusivity-consistency regularized multi-view subspace clustering. In: 2017 IEEE conference on Computer Vision and Pattern Recognition (CVPR), pp 1–9. https://doi.org/10.1109/CVPR.2017.8

  43. Kang Z, Guo Z, Huang S, Wang S, Chen W, Su Y, Xu Z (2019) Multiple partitions aligned clustering. In: Proceedings of the twenty-eighth International Joint Conference on Artificial Intelligence (IJCAI), pp 2701–2707. https://doi.org/10.24963/ijcai.2019/375

  44. Tang C, Sun K, Tang C, Zheng X, Liu X, Huang J-J, Zhang W (2023) Multi-view subspace clustering via adaptive graph learning and late fusion alignment. Neural Netw 165:333–343. https://doi.org/10.1016/j.neunet.2023.05.019

  45. Lv J, Kang Z, Wang B, Ji L, Xu Z (2021) Multi-view subspace clustering via partition fusion. Inf Sci 560:410–423. https://doi.org/10.1016/j.ins.2021.01.033

    Article  MathSciNet  Google Scholar 

  46. Chen H, Tai X, Wang W (2022) Multi-view subspace clustering with inter-cluster consistency and intra-cluster diversity among views. Appl Intell, 1–17. https://doi.org/10.1007/s10489-021-02895-1

  47. Chen M-S, Huang L, Wang C-D, Huang D, Yu PS (2022) Multiview subspace clustering with grouping effect. IEEE Trans Cybern 52(8):7655–7668. https://doi.org/10.1109/TCYB.2020.3035043

    Article  Google Scholar 

  48. Zhang C, Fu H, Hu Q, Cao X, Xie Y, Tao D, Xu D (2020) Generalized latent multi-view subspace clustering. IEEE Trans Pattern Anal Mach Intell 42(1):86–99. https://doi.org/10.1109/TPAMI.2018.2877660

    Article  Google Scholar 

  49. Qin Y, Feng G, Ren Y, Zhang X (2023) Consistency-induced multiview subspace clustering. IEEE Trans Cybern 53(2):832–844. https://doi.org/10.1109/TCYB.2022.3165550

    Article  Google Scholar 

  50. Qin Y, Pu N, Wu H (2023) Elastic multi-view subspace clustering with pairwise and high-order correlations. IEEE Trans Knowl Data Eng, 1–13. https://doi.org/10.1109/TKDE.2023.3293498

  51. Si X, Yin Q, Zhao X, Yao L (2022) Robust deep multi-view subspace clustering networks with a correntropy-induced metric. Appl Intell 52(13):14871–14887. https://doi.org/10.1007/s10489-022-03209-9

    Article  Google Scholar 

  52. Tang K, Xu K, Jiang W, Su Z, Sun X, Luo X (2023) Selecting the best part from multiple laplacian autoencoders for multi-view subspace clustering. IEEE Trans Knowl Data Eng 35(7):7457–7469. https://doi.org/10.1109/TKDE.2022.3178145

    Article  Google Scholar 

  53. Liu M, Wang Y, Palade V, Ji Z (2023) Multi-view subspace clustering network with block diagonal and diverse representation. Inf Sci 626:149–165. https://doi.org/10.1016/j.ins.2022.12.104

    Article  Google Scholar 

  54. Lu R-k, Liu J-w, Zuo X (2021) Attentive multi-view deep subspace clustering net. Neurocomputing 435:186–196. https://doi.org/10.1016/j.neucom.2021.01.011

    Article  Google Scholar 

  55. Roweis ST, Saul LK (2000) Nonlinear dimensionality reduction by locally linear embedding. Science 290(5500):2323–2326. https://doi.org/10.1126/science.290.5500.2323

    Article  Google Scholar 

  56. Nie F, Li J, Li X (2016) Parameter-free auto-weighted multiple graph learning: a framework for multiview clustering and semi-supervised classification. In: Proceedings of the twenty-fifth International Joint Conference on Artificial Intelligence (IJCAI), pp 1881–1887

  57. Wang H, Yang Y, Liu B (2020) Gmc: graph-based multi-view clustering. IEEE Trans Knowl Data Eng 32(6):1116–1129. https://doi.org/10.1109/TKDE.2019.2903810

    Article  Google Scholar 

  58. Van der Maaten L, Hinton G (2008) Visualizing data using t-sne. J Mach Learn Res 9(86):2579–2605

    Google Scholar 

Download references

Acknowledgements

This work was supported in part by the National Key R&D Program of China under Grant 2018AAA0100300; in part by the National Natural Science Foundation of China under Grant 61976041 and Grant 62076115; in part by the LiaoNing Revitalization Talents Program under Grant XLYC1907169; and in part by the Program of Star of Dalian Youth Science and Technology under Grant 2019RQ033 and Grant 2020RQ053.

Author information

Authors and Affiliations

  1. School of Mathematical Sciences, Dalian University of Technology, Dalian, 116024, Liaoning, China

    Kaiqiang Xu & Zhixun Su

  2. School of Mathematics, Liaoning Normal University, Dalian, 116029, Liaoning, China

    Kewei Tang

  3. Key Laboratory for Computational Mathematics and Data Intelligence of Liaoning Province, Dalian University of Technology, Dalian, 116024, Liaoning, China

    Zhixun Su

Authors
  1. Kaiqiang Xu
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Kewei Tang
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Zhixun Su
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding authors

Correspondence to Kewei Tang or Zhixun Su.

Ethics declarations

Conflict of Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Xu, K., Tang, K. & Su, Z. Multi-view deep subspace clustering via level-by-level guided multi-level features learning. Appl Intell 54, 11083–11102 (2024). https://doi.org/10.1007/s10489-024-05807-1

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10489-024-05807-1

Keywords