Abstract
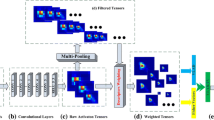
Fine-grained image recognition is characterized by high interclass object similarities and large intraclass object variations. Many existing works focus on locating more discriminative parts, but it is difficult to extract multigranular features synchronously and fuse them to make joint decisions about various granular parts. To address these issues, this work proposes a novel cross-granularity feature fusion method. First, a multi-granularity feature generator is used to obtain various granularity features simultaneously for mid-level feature maps via its subgenerators. The subgenerators divide the feature maps into blocks to ensure the relative integrity of the local features, and randomly shuffle the divided blocks to increase the variance of the local regions. Then, a cross-granularity feature fusion strategy achieves the joint decision-making of multiple granularity features in fine-grained images. Therefore, the proposed method can extract various granularity features and promote the synergistic interaction of richer granularity features. The effectiveness of the method is verified through comprehensive experiments on three widely-used fine-grained object recognition benchmark datasets and a chip inner structure dataset. The experimental results show that the proposed method significantly outperforms the baseline and exhibits a comparable performance to that of the SOTA method. Source codes are available at https://github.com/ShanWuJ/CGFF












Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Data Availability
The CHIP dataset that support the findings of this study are available from our institution. Restrictions apply to the availability of these data, which were used under license for this study. CHIP is available with the permission of our institution.
Code Availability
Source codes are available at https://github.com/ShanWuJ/CGFF
References
Ye S, Peng Q, Sun W, Xu J, Wang Y, You X, Cheung Y-M (2024) Discriminative suprasphere embedding for fine-grained visual categorization. IEEE Trans Neural Netw Learn Syst 35(4):5092–5102
Wei X-S, Song Y-Z, Aodha OM, Wu J, Peng Y, Tang J, Yang J, Belongie S (2022) Fine-grained image analysis with deep learning: A survey. IEEE Trans Pattern Anal Mach Intell 44(12):8927–8948
Zhang L, Huang S, Liu W, Tao D (2019) Learning a mixture of granularity-specific experts for fine-grained categorization. In: Proceedings of the IEEE/CVF international conference on computer vision pp 8331–8340
He X, Peng Y (2020) Fine-grained visual-textual representation learning. IEEE Trans Circ Syst Vid Technol 30(2):520–531
Zheng H, Fu J, Zha Z-J, Luo J, Mei T (2020) Learning rich part hierarchies with progressive attention networks for fine-grained image recognition. IEEE Trans Image Process 29:476–488
Sun G, Cholakkal H, Khan S, Khan F, Shao L (2020) Fine-grained recognition: Accounting for subtle differences between similar classes. In: Proceedings of the AAAI conference on artificial intelligence vol 34, pp 12047–12054
Zhang L, Huang S, Liu W (2022) Learning sequentially diversified representations for fine-grained categorization. Pattern Recognit 121:108219
Han J, Yao X, Cheng G, Feng X, Xu D (2022) P-cnn: Part-based convolutional neural networks for fine-grained visual categorization. IEEE Trans Pattern Anal Mach Intell 44(2):579–590
Guo C, Lin Y, Chen S, Zeng Z, Shao M, Li S (2022) From the whole to detail: Progressively sampling discriminative parts for fine-grained recognition. Knowl Based Syst 235:107651
Wang M, Zhao P, Lu X, Min F, Wang X (2023) Fine-grained visual categorization: A spatial–frequency feature fusion perspective. IEEE Trans Circ Syst Vid Technol 33(6):2798–2812
Wang S, Li H, Wang Z, Ouyang W (2021) Dynamic position-aware network for fine-grained image recognition. In: Proceedings of the AAAI conference on artificial intelligence vol 35, pp 2791–2799
Feng Y, Lv Y, Zhang H, Li F, He G (2022) Channel interaction mechanism for fine grained image categorization. In: 2022 International conference on image processing and media computing (ICIPMC), pp 115–119
Joung S, Kim S, Kim M, Kim I-J, Sohn K (2021) Learning canonical 3d object representation for fine-grained recognition. In: 2021 IEEE/CVF international conference on computer vision (ICCV), pp 1015–1025
Luo W, Yang X, Mo X, Lu Y, Davis LS, Li J, Yang J, Lim S-N (2019) Cross-x learning for fine-grained visual categorization. In: Proceedings of the IEEE/CVF international conference on computer vision, pp 8242–8251
Huang S, Wang X, Tao D (2021) Stochastic partial swap: Enhanced model generalization and interpretability for fine-grained recognition. In: Proceedings of the IEEE/CVF international conference on computer vision pp 620–629
Yang X, Zeng Z, Yang D (2024) Adaptive mid-level feature attention learning for fine-grained ship classification in optical remote sensing images. IEEE Trans Geosci Remote Sens 62:1–10
Du R, Chang D, Bhunia AK, Xie J, Ma Z, Song Y-Z, Guo J (2020) Fine-grained visual classification via progressive multi-granularity training of jigsaw patches. In: European conference on computer vision, pp 153–168. Springer
Zhang Y, Sun Y, Wang N, Gao Z, Chen F, Wang C, Tang J (2021) Msec: Multi-scale erasure and confusion for fine-grained image classification. Neurocomputing 449:1–14
An C, Wang X, Wei Z, Zhang K, Huang L (2023) Multi-scale network via progressive multi-granularity attention for fine-grained visual classification. Appl Soft Comput 146:110588
Xu Y, Wu S, Wang B, Yang M, Wu Z, Yao Y, Wei Z (2024) Two-stage fine-grained image classification model based on multi-granularity feature fusion. Pattern Recognit 146:110042
Stockman G, Shapiro LG (2001) Computer Vision. Prentice Hall PTR, Englewood Cliffs, NJ, USA
Gonzalez RC, Woods RE (2018) Digital Image Processing, 4th edn. Pearson, New York, USA
Ji R, Wen L, Zhang L, Du D, Wu Y, Zhao C, Liu X, Huang F (2020) Attention convolutional binary neural tree for fine-grained visual categorization. In: 2020 IEEE/CVF conference on computer vision and pattern recognition (CVPR), pp 10465–10474
Liu H, Li J, Li D, See J, Lin W (2021) Learning scale-consistent attention part network for fine-grained image recognition. IEEE Trans Multimed 24:2902–2913
He J, Chen J-N, Liu S, Kortylewski A, Yang C, Bai Y, Wang C (2022) Transfg: A transformer architecture for fine-grained recognition. In: Proceedings of the AAAI conference on artificial intelligence vol 36, pp 852–860
Sun H, He X, Peng Y (2022) Sim-trans: Structure information modeling transformer for fine-grained visual categorization. In: Proceedings of the 30th ACM international conference on multimedia, pp 5853–5861
Chang D, Pang K, Zheng Y, Ma Z, Song Y-Z, Guo J (2021) Your “flamingo” is my “bird”: Fine-grained, or not. In: 2021 IEEE/CVF conference on computer vision and pattern recognition (CVPR) pp 11471–11480
Zhu Q, Li Z, Kuang W, Ma H (2023) A multichannel location-aware interaction network for visual classification. Appl Intell 53(20):23049–23066
Chen H, Cheng L, Huang G, Zhang G, Lan J, Yu Z, Pun C-M, Ling W-K (2022) Fine-grained visual classification with multi-scale features based on self-supervised attention filtering mechanism. Appl Intell 52(13):15673–15689
Chang D, Ding Y, Xie J, Bhunia AK, Li X, Ma Z, Wu M, Guo J, Song Y-Z (2020) The devil is in the channels: Mutual-channel loss for fine-grained image classification. IEEE Trans Image Process 29:4683–4695
Xu M, Qin L, Chen W, Pu S, Zhang L (2023) Multi-view adversarial discriminator: Mine the non-causal factors for object detection in unseen domains. In: Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, pp 8103–8112
Deng W, Marsh J, Gould S, Zheng L (2022) Fine-grained classification via categorical memory networks. IEEE Trans Image Process 31:4186–4196
Min S, Yao H, Xie H, Zha Z-J, Zhang Y (2020) Multi-objective matrix normalization for fine-grained visual recognition. IEEE Trans Image Process 29:4996–5009
Sun L, Guan X, Yang Y, Zhang L (2020) Text-embedded bilinear model for fine-grained visual recognition. In: Proceedings of the 28th ACM international conference on multimedia, pp 211–219
Tan M, Yuan F, Yu J, Wang G, Gu X (2022) Fine-grained image classification via multi-scale selective hierarchical biquadratic pooling. ACM Trans Multimed Comput Commun Appl (TOMM) 18(1s):1–23
Chen Y, Bai Y, Zhang W, Mei T (2019) Destruction and construction learning for fine-grained image recognition. In: Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, pp 5157–5166
Zhang K, Fan J, Huang S, Qiao Y, Yu X, Qin F (2022) Cekd: Cross ensemble knowledge distillation for augmented fine-grained data. Appl Intell 52(14):16640–16650
Ma L, Zhao F, Hong H, Wang L, Zhu Y (2023) Complementary parts contrastive learning for fine-grained weakly supervised object co-localization. IEEE Trans Circ Syst Vid Technol 1:1
Wang L, He K, Feng X, Ma X (2022) Multilayer feature fusion with parallel convolutional block for fine-grained image classification. Appl Intell 52(3):2872–2883
Xu K, Lai R, Gu L, Li Y (2023) Multiresolution discriminative mixup network for fine-grained visual categorization. IEEE Trans Neural Netw Learn Syst 34(7):3488–3500
Wan R, Zhou J, Huang B, Zeng H, Fan Y (2022) Apmc: Adjacent pixels based measurement coding system for compressively sensed images. IEEE Trans Multimed 24:3558–3569
Wah C, Branson S, Welinder P, Perona P, Belongie S (2011) The caltech-ucsd birds-200-2011 dataset
Krause J, Stark M, Deng J, Fei-Fei L (2013) 3d object representations for fine-grained categorization. In: Proceedings of the IEEE international conference on computer vision workshops, pp 554–561
Maji S, Rahtu E, Kannala J, Blaschko M, Vedaldi A (2013) Fine-grained visual classification of aircraft. arXiv:1306.5151
He K, Zhang X, Ren S, Sun J (2016) Deep residual learning for image recognition. In: Proceedings of the IEEE conference on computer vision and pattern recognition, pp 770–778
Deng J, Dong W, Socher R, Li L-J, Li K, Fei-Fei L (2009) Imagenet: A large-scale hierarchical image database. In: 2009 IEEE conference on computer vision and pattern recognition, pp 248–255
Liu K, Chen K, Jia K (2022) Convolutional fine-grained classification with self-supervised target relation regularization. IEEE Trans Image Process 31:5570–5584
Selvaraju RR, Cogswell M, Das A, Vedantam R, Parikh D, Batra D (2017) Grad-cam: Visual explanations from deep networks via gradient-based localization. In: Proceedings of the IEEE international conference on computer vision, pp 618–626
Acknowledgements
This work was supported by the Fund of the National Key Laboratory for Reliability Physics and Its Application Technology of Electrical Component, under grant 6142806230201, the National Natural Science Foundation of China, under grant 62221005, 62276038, and the Key Cooperation Project of Chongqing Municipal Education Commission, under grant HZ2021008.
Author information
Authors and Affiliations
Contributions
All authors contributed to the study conception and design. Shan Wu contributed to the conception, data curation, formal analysis, methodology, software, validation and drafted the manuscript. Jun Hu contributed to the conception, data curation, methodology, and critically revised the manuscript. Chen Sun contributed to data curation, funding, methodology, resources, supervision, and revised the manuscript. Fujin Zhong contributed to the conception, methodology, and revised the manuscript. Qinghua Zhang contributed to the conception, funding, and revised the manuscript. Guoyin Wang contributed to the conception, methodology, project administration, supervision, funding, and revised the manuscript. All authors read and approved the final manuscript, and agreed to be accountable for all aspects of the work, ensuring that anyquestions related to the accuracy or integrity of the study are appropriately addressed and resolved.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
A local region \(f_{loc}\) of size \((m+k) \times (m+k)\) is represented as (A1) in \(f^{1 \times n\times n}(x)\).
where \((i+m+k-1) \le n\) and \((j+m+k-1) \le n. i,j\in \{1,2,\dots ,n\}\). The variance of the local region \(f_{loc}\) is given by (A2).
To explain it more clearly, \(\sigma ^2_{f_{loc}}\) is transformed as the following (A3).
The resulting local region \(f_{loc}^{'}\) after exchanged is represented as (A4).
where \(r,h\in \{1,2,\dots ,n\},r+m-1\le n,h+m-1\le n\). The variance \(\sigma ^2_{f^{'}_{loc}}\) of the local region \(f^{'}_{loc}\) can be obtained through the same method as before (2).
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Wu, S., Hu, J., Sun, C. et al. A cross-granularity feature fusion method for fine-grained image recognition. Appl Intell 55, 42 (2025). https://doi.org/10.1007/s10489-024-05891-3
Accepted:
Published:
DOI: https://doi.org/10.1007/s10489-024-05891-3