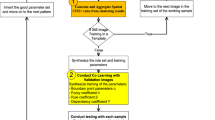
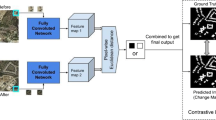
Abstract
To enhance the efficacy of change detection in remote sensing images, we propose a novel Spatial Complex Fuzzy Inference System (Spatial CFIS). This system incorporates fuzzy clustering to generate complex fuzzy rules and employs a triangular spatial complex fuzzy rule base to predict changes in subsequent images compared to their original versions. The weight set of the rule base is optimized using the ADAM algorithm to boost the overall performance of Spatial CFIS. Our proposed model is evaluated using datasets from the weather image data warehouse of the USA Navy and the PRISMA mission funded by the Italian Space Agency (ASI). We compare the performance of Spatial CFIS against other relevant algorithms, including PFC-PFR, SeriesNet, and Deep Slow Feature Analysis (DSFA). The evaluation metrics include RMSE (Root Mean Squared Error), R2 (R Squared), and Analysis of Variance (ANOVA). The experimental results demonstrate that Spatial CFIS outperforms other models by up to 40% in terms of accuracy. In summary, this paper presents an innovative approach to handling remote sensing images by applying a spatial-oriented fuzzy inference system, offering improved accuracy in change detection.













Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Data availability
The data that support the findings of this study are available from the US Navy and Prisma project, but restrictions apply to the availability of these data, which were used under license for the current study, and so are not publicly available. Data are, however, available from the authors upon reasonable request and with permission of the US Navy and Prisma project.
Code availability
Source codes and Dataset of this paper are available at the following address: https://github.com/vietdslab/SpatialCFIS
References
Zhang C, Wei S, Ji S, Lu M (2019) Detecting large-scale urban land cover changes from very high resolution remote sensing images using cnn-based classification. ISPRS Int J Geo Inf 8(4):189
Atluri G, Karpatne A, Kumar V (2018) Spatio-temporal data mining: A survey of problems and methods. ACM Computing Surveys (CSUR) 51(4):1–41
Tariq A, Mumtaz F (2023) Modeling spatio-temporal assessment of land use land cover of lahore and its impact on land surface temperature using multi-spectral remote sensing data. Environ Sci Pollut Res 30(9):23908–23924
Muhammad R, Zhang W, Abbas Z, Guo F, Gwiazdzinski L (2022) Spatiotemporal change analysis and prediction of future land use and land cover changes using qgis molusce plugin and remote sensing big data: a case study of linyi, china. Land 11(3):419
Lv Z, Huang H, Gao L, Benediktsson JA, Zhao M, Shi C (2022) Simple multiscale unet for change detection with heterogeneous remote sensing images. IEEE Geosci Remote Sens Lett 19:1–5
Jimenez-Sierra DA, Quintero-Olaya DA, Alvear-Munoz JC, Benitez-Restrepo HD, Florez-Ospina JF, Chanussot J (2022) Graph learning based on signal smoothness representation for homogeneous and heterogeneous change detection. IEEE Trans Geosci Remote Sens 60:1–16
Lv Z, Huang H, Li X, Zhao M, Benediktsson JA, Sun W, Falco N (2022) Land cover change detection with heterogeneous remote sensing images: Review, progress, and perspective. Proceedings of the IEEE
Zhang H, Yu C, Jin Y (2020) A novel method for classifying function of spatial regions based on two sets of characteristics indicated by trajectories. Int J Data Warehous Min (IJDWM) 16(3):1–19
Jacob IJ, Paulraj B, Darney PE, Long HV, Tuan TM, Yesudhas HR, Shanmuganathan V, Eanoch GJ (2021) Image retrieval using intensity gradients and texture chromatic pattern: Satellite images retrieval. Int J Data Warehous Min (IJDWM) 17(1):57–73
Zheng Y, Zhang X, Hou B, Liu G (2013) Using combined difference image and \( k \)-means clustering for sar image change detection. IEEE Geosci Remote Sens Lett 11(3):691–695
Li W, Pang B, Xu X, Wei B (2022) A sar change detection method based on an iterative guided filter and the log mean ratio. Remote Sensing Letters 13(7):663–671
Shen W, Jia Y, Wang Y, Lin Y, Li Y (2022) Spaceborne sar time-series images change detection based on log-ratio operator. In: 2022 IEEE 5th International Conference on Computer and Communication Engineering Technology (CCET), pp 80–83. IEEE
Pal R, Mukhopadhyay S, Chakraborty D, Suganthan PN (2022) Very high-resolution satellite image segmentation using variable-length multi-objective genetic clustering for multi-class change detection. J King Saud University-Comp Inf Sci 34(10):9964–9976
Aghamohammadi A, Ranjbarzadeh R, Naiemi F, Mogharrebi M, Dorosti S, Bendechache M (2021) Tpcnn: two-path convolutional neural network for tumor and liver segmentation in ct images using a novel encoding approach. Expert Syst Appl 183:115406
Seydi ST, Shah-Hosseini R, Amani M (2022) A multi-dimensional deep siamese network for land cover change detection in bi-temporal hyperspectral imagery. Sustainability 14(19):12597
Zou L, Li M, Cao S, Yue F, Zhu X, Li Y, Zhu Z (2022) Object-oriented unsupervised change detection based on neighborhood correlation images and k-means clustering for the multispectral and high spatial resolution images. Can J Remote Sens 48(3):441–451
Kumar JT, Yennapusa MR, Rao BP (2022) Tri-su-l adwt-fcm: Tri-su-l-based change detection in sar images with adwt and fuzzy c-means clustering. J Indian Soc Remote Sens 50(9):1667–1687
Zare H, Weber TK, Ingwersen J, Nowak W, Gayler S, Streck T (2022) Combining crop modeling with remote sensing data using a particle filtering technique to produce real-time forecasts of winter wheat yields under uncertain boundary conditions. Remote Sens 14(6):1360
Son LH, Thong PH (2017) Some novel hybrid forecast methods based on picture fuzzy clustering for weather nowcasting from satellite image sequences. Appl Intell 46:1–15
Kingma DP, Ba J (2014) Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980
Kalaiselvi S, Gomathi V (2020) \(\alpha \)-cut induced fuzzy deep neural network for change detection of sar images. Appl Soft Comput 95:106510
Zhang X, Han L, Han L, Zhu L (2020) How well do deep learning-based methods for land cover classification and object detection perform on high resolution remote sensing imagery? Remote Sens 12(3):417
Dai J, Wang Y, Li W, Zuo Y (2020) Automatic method for extraction of complex road intersection points from high-resolution remote sensing images based on fuzzy inference. IEEE Access 8:39212–39224
Sharifi E, Mazinan A (2018) On transient stability of multi-machine power systems through takagi-sugeno fuzzy-based sliding mode control approach. Compl Intell Syst 4:171–179
Rezaei Kalantari K, Ebrahimnejad A, Motameni H (2020) Presenting a new fuzzy system for web service selection aimed at dynamic software rejuvenation. Compl Intell Syst 6(3):697–710
Karampour M, Halabian A, Hosseini A, Mosapoor M (2023) Comparing the performance of fuzzy operators in the object-based image analysis and support vector machine kernel functions for the snow cover estimation in alvand mountain. Theoretical and Applied Climatology, 1–9
Tian D, Gong M (2018) A novel edge-weight based fuzzy clustering method for change detection in sar images. Inf Sci 467:415–430
Su L, Gong M, Zhang P, Zhang M, Liu J, Yang H (2017) Deep learning and mapping based ternary change detection for information unbalanced images. Pattern Recogn 66:213–228
Huang B, Zhao B, Song Y (2018) Urban land-use mapping using a deep convolutional neural network with high spatial resolution multispectral remote sensing imagery. Remote Sens Environ 214:73–86
Chen T-CT, Wu H-C (2020) Forecasting the unit cost of a dram product using a layered partial-consensus fuzzy collaborative forecasting approach. Compl Intell Syst 6:479–492
Chen T, Chiu M-C (2021) An interval fuzzy number-based fuzzy collaborative forecasting approach for dram yield forecasting. Compl Intell Syst 7:111–122
Selvachandran G, Quek SG, Lan LTH, Giang NL, Ding W, Abdel-Basset M, De Albuquerque VHC et al (2019) A new design of mamdani complex fuzzy inference system for multiattribute decision making problems. IEEE Trans Fuzzy Syst 29(4):716–730
Tuan TM, Lan LTH, Chou S-Y, Ngan TT, Son LH, Giang NL, Ali M (2020) M-cfis-r: Mamdani complex fuzzy inference system with rule reduction using complex fuzzy measures in granular computing. Mathematics 8(5):707
Lan LTH, Tuan TM, Ngan TT, Giang NL, Ngoc VTN, Van Hai P et al (2020) A new complex fuzzy inference system with fuzzy knowledge graph and extensions in decision making. Ieee Access 8:164899–164921
Yazdanbakhsh O, Dick S (2019) Fancfis: Fast adaptive neuro-complex fuzzy inference system. Int J Approximate Reasoning 105:417–430
Liu Y, Liu F (2019) An adaptive neuro-complex-fuzzy-inferential modeling mechanism for generating higher-order tsk models. Neurocomputing 365:94–101
Mei Z, Zhao T, Xie X (2024) Hierarchical fuzzy regression tree: A new gradient boosting approach to design a tsk fuzzy model. Inf Sci 652:119740
Gulistan M, Khan S (2020) Extentions of neutrosophic cubic sets via complex fuzzy sets with application. Compl Intell Syst 6:309–320
Firozja MA, Agheli B, Jamkhaneh EB (2020) A new similarity measure for pythagorean fuzzy sets. Compl Intell Syst 6(1):67–74
Liu S, Kong W, Chen X, Xu M, Yasir M, Zhao L, Li J (2022) Multi-scale ship detection algorithm based on a lightweight neural network for spaceborne sar images. Remote Sens 14(5):1149
Ma W, Xiong Y, Wu Y, Yang H, Zhang X, Jiao L (2019) Change detection in remote sensing images based on image mapping and a deep capsule network. Remote Sens 11(6):626
Lv Z, Liu T, Shi C, Benediktsson JA, Du H (2019) Novel land cover change detection method based on k-means clustering and adaptive majority voting using bitemporal remote sensing images. Ieee Access 7:34425–34437
Peng D, Zhang Y, Guan H (2019) End-to-end change detection for high resolution satellite images using improved unet++. Remote Sens 11(11):1382
Ecer F, Ögel İY, Krishankumar R, Tirkolaee EB (2023) The q-rung fuzzy lopcow-vikor model to assess the role of unmanned aerial vehicles for precision agriculture realization in the agri-food 4.0 era. Artificial Intelligence Review, 1–34
Wan L, Xiang Y, You H (2019) A post-classification comparison method for sar and optical images change detection. IEEE Geosci Remote Sens Lett 16(7):1026–1030
Yang M, Jiao L, Liu F, Hou B, Yang S (2019) Transferred deep learning-based change detection in remote sensing images. IEEE Trans Geosci Remote Sens 57(9):6960–6973
Yang G, Li H-C, Wang W-Y, Yang W, Emery WJ (2019) Unsupervised change detection based on a unified framework for weighted collaborative representation with rddl and fuzzy clustering. IEEE Trans Geosci Remote Sens 57(11):8890–8903
Bezdek JC, Ehrlich R, Full W (1984) Fcm: The fuzzy c-means clustering algorithm. Computers & Geosciences 10(2):191–203. https://doi.org/10.1016/0098-3004(84)90020-7
Yetgin Z (2011) Unsupervised change detection of satellite images using local gradual descent. IEEE Trans Geosci Remote Sens 50(5):1919–1929
Shen Z, Zhang Y, Lu J, Xu J, Xiao G (2018) Seriesnet: a generative time series forecasting model. In: 2018 International Joint Conference on Neural Networks (IJCNN), pp 1–8. IEEE
Du B, Ru L, Wu C, Zhang L (2019) Unsupervised deep slow feature analysis for change detection in multi-temporal remote sensing images. IEEE Trans Geosci Remote Sens 57(12):9976–9992
Wu T, Toet A (2014) Color-to-grayscale conversion through weighted multiresolution channel fusion. J Electron Imaging 23(4):043004–043004
Oceanic N, Administration A (2023) MTSAT West Color Infrared Loop - https://www.star.nesdis.noaa.gov/GOES/index.php
(ASI) ISA. PRISMA: Small Innovative Earth Observation Mission - . https://www.asi.it/en/earth-science/prisma
Acknowledgements
This research has been funded by the Research Project:22-2024-RD/HĐ-ĐHCN, Hanoi University of Industry; CSCL34.01/22-23, Space Technology Institute - Vietnam Academy of Science and Technology.
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Conflict of interest
The authors declare that they do not have any conflict of interest. All authors have checked and agreed on the submission
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A Appendix
Appendix A Appendix
1.1 A.1 Numerical examples
In this subsection, we present a numerical example to describe the steps of the Spatial CFIS algorithm in Section 4.2.
-
1.
Step 1. Pre-processing data
-
(a)
Input Image Data include 3x3 images can be replaced by 1x9 images below: Image 1: [36, 47, 42, 48, 67, 74, 55, 52, 46] Image 2: [36, 42, 43, 58, 59, 84, 55, 54, 41] Image 3: [32, 41, 36, 48, 54, 77, 65, 64, 31] Image 4: [33, 40, 37, 58, 62, 80, 59, 71, 36] Image 5: [34, 42, 27, 55, 52, 72, 58, 66, 39]
-
(b)
Step 1.1. Convert satellite color images to gray images As the input image data utilized in the presented example is already in grayscale format, there is no requirement for any additional conversion procedures.
-
(c)
Step 1.2. Determine difference matrix (Imaginary part) Imaginary part (difference matrix): determined by subtracting the correspondent pixel in the satellite image by equation
$$ HoD_i = X^{(t)}-X^{(t-1)} $$\(HoD_1\)(Image 2 - Image 1): [0, 5, 1, 10, 8, 10, 0, 2, 5] \(HoD_2\)(Image 3 - Image 2): [4, 1, 7, 10, 5, 7, 10, 10, 10] \(HoD_3\)(Image 4 - Image 3): [1, 1, 1, 10, 8, 3, 6, 7, 5] \(HoD_4\)(Image 5 - Image 4): [1, 2, 10, 3, 10, 8, 1, 5, 3] Our data now are in the form that: \({X}'<{{X}^{(t)}}, HoD>\)
-
(a)
-
2.
Step 2: Clustering We apply fuzzy clustering for both X(t) and HoD. Inputs can be represented as: \(X_1: [(36, 0), (47, 5), (42,1), (48,10), (67, 8), (74,10),\) \( (55, 0), (52, 2), (46, 5)]\) \(X_2: [(36, 4), (42, 1), (43, 7), (58, 10), (59, 5), (84, 7),\) \( (55,10), (54,10), (41,1)]\) \(X_3: [(32, 1), (41, 1), (36, 1), (48, 10), (54, 8), (77, 3),\) \( (65, 6), (64, 7), (31, 5)]\) \(X_4: [(33, 1), (40, 2), (37, 10), (58, 3), (62, 10), (80, 8),\) \( (59, 1), (71, 5), (36, 3)]\) With the parameters \(C = 2, m = 2, \varepsilon = 0.001\) (threshold of two consecutive output) and \(maxstep = 3\) (number of iterators). Output: - Membership matrix U. - The center of cluster V.
- (a):
-
Step 2.1: Recalculate X(t) and HoD values shows a returned value in the range [0,1] Because the values of each pixel of the gray image are in the range of [0, 255], we divide each one by 225. \(X_1\): [(0.1412, 0), (0.1843, 0.0196), (0.1647, 0.0039), (0.1882, 0.0392), (0.2627, 0.0314), (0.2902, 0.0392), (0.2157, 0), (0.2039, 0.0078), (0.1804, 0.0196)]; \(X_2\): [(0.1412, 0.0157), (0.1647, 0.0039), (0.1686, 0.0275), (0.2275, 0.0392), (0.2314, 0.0196), (0.3294, 0.0275), (0.2157, 0.0392), (0.2118, 0.0392), (0.1608, 0.0392)]; \(X_3\): [(0.1255, 0.0039), (0.1608, 0.0039), (0.1412, 0.0039), (0.1882, 0.0392), (0.2118, 0.0314), (0.302, 0.0118), (0.2549, 0.0235), (0.251, 0.0275), (0.1216, 0.0196)]; \(X_4\): [(0.1294, 0.0039), (0.1569, 0.0078), (0.1451, 0.0392), (0.2275, 0.0118), (0.2431, 0.0392), (0.3137, 0.0314), (0.2314, 0.0039), (0.2784, 0.0196), (0.1412, 0.0118)].
- (b):
-
Step 2.2: Initiate the centers of cluster matrix V randomly satisfied: – Let \(V_j\) be the center of cluster j, \({{V}_{j1}}\in \left( \min Xi,\dots \right. \) \(\left. \max Xi \right) ;{{V}_{j2}}\in \left( \min HoD_i,...\max HoD_i \right) \) then
$$V_{ }^{(0)}=\,\left[ \begin{array}{*{35}{r}} 0.1416 & 0.1744 \\ 0.0024 & 0.0113 \\ \end{array} \right] $$ - (c):
-
Step 2.3: Calculate the degrees of membership matrix U by the cluster center V: Calculate the values of U as a function of the cluster center vector V, using formula (6) as follows:
$$\begin{aligned} {{U}_{11}}= & \frac{1}{{{\left( \frac{\sqrt{{{\left( {{X}_{11}}-{{V}_{11}} \right) }^{2}}+{{\left( {{X}_{12}}-{{V}_{12}} \right) }^{2}}}}{\sqrt{{{\left( {{X}_{11}}-{{V}_{11}} \right) }^{2}}+{{\left( {{X}_{12}}-{{V}_{12}} \right) }^{2}}}} \right) }^{\frac{2}{2-1}}}+{{\left( \frac{\sqrt{{{\left( {{X}_{11}}-{{V}_{11}} \right) }^{2}}+{{\left( {{X}_{12}}-{{V}_{12}} \right) }^{2}}}}{\sqrt{{{\left( {{X}_{11}}-{{V}_{21}} \right) }^{2}}+{{\left( {{X}_{12}}-{{V}_{22}} \right) }^{2}}}} \right) }^{\frac{2}{2-1}}}}\,\\ {{U}_{12}}= & \frac{1}{{{\left( \frac{\sqrt{{{\left( {{X}_{11}}-{{V}_{21}} \right) }^{2}}+{{\left( {{X}_{12}}-{{V}_{22}} \right) }^{2}}}}{\sqrt{{{\left( {{X}_{11}}-{{V}_{11}} \right) }^{2}}+{{\left( {{X}_{12}}-{{V}_{12}} \right) }^{2}}}} \right) }^{\frac{2}{2-1}}}+{{\left( \frac{\sqrt{{{\left( {{X}_{11}}-{{V}_{21}} \right) }^{2}}+{{\left( {{X}_{12}}-{{V}_{22}} \right) }^{2}}}}{\sqrt{{{\left( {{X}_{11}}-{{V}_{21}} \right) }^{2}}+{{\left( {{X}_{12}}-{{V}_{22}} \right) }^{2}}}} \right) }^{\frac{2}{2-1}}}}\\ {{U}^{(0)}}= & \left[ \begin{array}{*{35}{r}} 0.9952 & 0.0048 \\ 0.073 & 0.927 \\ 0.2174 & 0.7826 \\ 0.2156 & 0.7844 \\ 0.3459 & 0.6541 \\ 0.3771 & 0.6229 \\ 0.2501 & 0.7499 \\ 0.1841 & 0.8159 \\ 0.055 & 0.945 \\ \end{array} \right] \end{aligned}$$ - (d):
-
Step 2.4: Update center of clusters Using the formulas for cluster center calculation (5), we recalculate the values of the new cluster centers based on the membership degrees U computed in Step 2.3 as follows:
$$\begin{aligned} {{V}_{J1}}= & \frac{\sum \limits _{k=1}^{N}{\mathop {U}_{kj}^{m} \times {{X}_{k}}}}{\sum \limits _{k=1}^{N}{\mathop {U}_{kj}^{m}}};{{V}_{J2}}=\,\frac{\sum \limits _{k=1}^{N}{\mathop {U}_{kj}^{m} \times HoD}_{k}}{\sum \limits _{k=1}^{N}{\mathop {U}_{kj}^{m}}}\\ V_{j1}^{(1)}= & \left[ \begin{array}{*{35}{r}} 0.173 \\ 0.0081 \\ \end{array} \right] ; V_{j2}^{(1)}=\,\left[ \begin{array}{*{35}{r}} 0.2027 \\ 0.0188 \\ \end{array} \right] \\ V_{ }^{(1)}= & \left[ \begin{array}{*{35}{r}} 0.173 & 0.2027 \\ 0.0081 & 0.0188 \\ \end{array} \right] \end{aligned}$$Calculate the difference between \(V^{1}\) and \(V^{0}\) by using Euclidean formula:
$$\begin{aligned} & \left\| {{V}^{(1)}}\,-\,{{V}^{(0)}}\, \right\| =\sqrt{\sum \nolimits _{l=1}^{2}{{{(V_{jl}^{(1)}-V_{jl}^{(0)})}^{2}}}} \\= & \sqrt{{{(V_{j1}^{(1)}-V_{j1}^{(0)})}^{2}}+{{(V_{j2}^{(1)}-V_{j2}^{(0)})}^{2}}}\\= & \sqrt{{{(V_{11}^{(1)}-V_{11}^{(0)})}^{2}}+{{(V_{12}^{(1)}-V_{12}^{(0)})}^{2}}+{{(V_{21}^{(1)}-V_{21}^{(0)})}^{2}}+{{(V_{22}^{(1)}-V_{22}^{(0)})}^{2}}}\\= & 0.2623 \end{aligned}$$ - (e):
-
Step 2.5 Repeat steps 2 and 3 until one of the two following conditions are not satisfied: – Condition 1: The number of iterations is less than the max step. – Condition 2: \(\vert V^{(t)}\,-\,V^{(t-1)}\, \vert \, \le \varepsilon =0.0001\) Because Number of iteration is 1 and \(\left\| {{V}^{(1)}}\,-\,{{V}^{(0)}}\, \right\| \) \(= 0.2623 < \varepsilon \) we continue iteration 2.
$$ {{U}^{(1)}}=\,\left[ \begin{array}{*{35}{r}} 0.3003 & 0.6997 \\ 0.4799 & 0.5201 \\ 0.3846 & 0.6154 \\ 0.5492 & 0.4508 \\ 0.6348 & 0.3652 \\ 0.6641 & 0.3359 \\ 0.5031 & 0.4969 \\ 0.4969 & 0.5031 \\ 0.4692 & 0.5308 \\ \end{array} \right] ; V_{ }^{(2)}=\,\left[ \begin{array}{*{35}{r}} 0.2206 & 0.187 \\ 0.0227 & 0.013 \\ \end{array} \right] $$Calculate the difference between \(V^{2}\) and \(V^{1}\) by using Euclidean formula: . Since the number of iterations is 2 and \(\left\| {{V}^{(2)}}\,-\,{{V}^{(1)}}\, \right\| \, = 0.2583 < \varepsilon \). We continue the iteration 3:
$${{U}^{(2)}}=\,\left[ \begin{array}{*{35}{r}} 0.2495 & 0.7505 \\ 0.0369 & 0.9631 \\ 0.1429 & 0.8571 \\ 0.3422 & 0.6578 \\ 0.7666 & 0.2334 \\ 0.689 & 0.311 \\ 0.648 & 0.352 \\ 0.3843 & 0.6157 \\ 0.0509 & 0.9491 \\ \end{array} \right] ; V_{ }^{(3)}=\,\left[ \begin{array}{*{35}{r}} 0.2442 & 0.1808 \\ 0.0234 & 0.0152 \\ \end{array} \right] $$Calculate the difference between \(V^{3}\) và \(V^{2}\) by using Euclidean formula: \(\left\| {{V}^{(2)}}-{{V}^{(1)}} \right\| = 0.0245 < \varepsilon \). Since the number of iterations is 3 and \(\left\| {{V}^{(2)}}-{{V}^{(1)}} \right\| = 0.0245 < \varepsilon \), we stop the algorithm because the number of iterations equals to maxstep. The final result of this example is shown as below:
$$U=\,\left[ \begin{array}{*{35}{r}} 0.2495 & 0.7505 \\ 0.0369 & 0.9631 \\ 0.1429 & 0.8571 \\ 0.3422 & 0.6578 \\ 0.7666 & 0.2334 \\ 0.689 & 0.311 \\ 0.648 & 0.352 \\ 0.3843 & 0.6157 \\ 0.0509 & 0.9491 \\ \end{array} \right] ; V=\,\left[ \begin{array}{*{35}{r}} 0.2442 & 0.1808 \\ 0.0234 & 0.0152 \\ \end{array} \right] $$
-
3.
Step 3: Finding rules using Triangular fuzzy method Determining the value of \(a, b, c, a', b', c'\) of input data \(X_1^{'}\): The value of b and \(b'\) can be defined by the center of cluster matrix (\(b_{kj}=V_j\))
$$\begin{aligned} {{b}_{1}}= & {{V}_{11}};{{b}_{2}}=\,{{V}_{21}};{{{b}'}_{1}}=\,{{V}_{12}};{{{b}'}_{2}}=\,{{V}_{22}};\\ {{a}_{kj}}= & \frac{\sum \limits _{i=1,2,\,\,...n\,\,\text {v}\grave{\textrm{a}}\,\,I_{i}^{(k)}\,\le \,{{b}_{kj}}}{{{U}_{\text {i,j}}}\times \,I_{i}^{(k)}}}{\sum \limits _{i=1,2,\,\,...n\,\,\text {v}\grave{\textrm{a}}\,\,I_{i}^{(k)}\,\le \,{{b}_{kj}}}{{{U}_{\text {i,j}}}}}\\ {{c}_{kj}}= & \frac{\sum \limits _{i=1,2,\,\,...n\,\,\text {v}\grave{\textrm{a}}\,\,I_{i}^{(k)}\,\ge \,{{b}_{kj}}}{{{U}_{\text {i,j}}}\times \,I_{i}^{(k)}}}{\sum \limits _{i=1,2,\,\,...n\,\,\text {v}\grave{\textrm{a}}\,\,I_{i}^{(k)}\,\ge \,{{b}_{kj}}}{{{U}_{\text {i,j}}}}} \end{aligned}$$Incorporating the real parts values of \(I_{i}^{(k)}\), we obtain \(a_1=0.1926\), \(a_2=0.1636\), \(c_1=0.2757\), and \(c_2=0.2089\).
$$\begin{aligned} {{{a}'}_{kj}}= & \frac{\sum \limits _{i=1,2,\,\,...n\,\,\text {v}\grave{\textrm{a}}\,\,HoD_{i}^{(k)}\,\le \,{{b}_{kj}}}{{{U}_{\text {i,j}}}\times HoD_{i}^{(k)}}}{\sum \limits _{i=1,2,\,\,...n\,\,\text {v}\grave{\textrm{a}}\,\,HoD_{i}^{(k)}\,\le \,{{b}_{kj}}}{{{U}_{\text {i,j}}}}}\\ {{{c}'}_{kj}}= & \frac{\sum \limits _{i=1,2,\,\,...n\,\,\text {v}\grave{\textrm{a}}\,\,I_{i}^{(k)}\,\ge \,{{b}_{kj}}}{{{U}_{\text {i,j}}}\times HoD_{i}^{(k)}}}{\sum \limits _{i=1,2,\,\,...n\,\,\text {v}\grave{\textrm{a}}\,\,HoD_{i}^{(k)}\,\ge \,{{b}_{kj}}}{{{U}_{\text {i,j}}}}} \end{aligned}$$Using the imaginary parts values \(HoD_{i}^{(k)}\), we obtain \(a'_1=0.0035\), \(a'_2=0.0032\), \(c'_1=0.0359\), and \(c'_2=0.0266\). Similar with the other imaginary parts. We can assume the rule for the first input data below: Rule 1: includes 6 parameters a, b, c and \(a', b', c'\) where a, b and c are corresponding to the first triangle of real part and \(a', b'\) and \(c'\) are corresponding to the first triangle of imaginary part.
$$\begin{aligned} (a,\,b,\,c,\,{a}',\,{b}',\,{c}')=\left[ {{a}_{1}},\,{{b}_{1}},{{c}_{1}},{{{{a}'}}_{1}},{{{{b}'}}_{1}},{{{{c}'}}_{1}} \right] \end{aligned}$$$$\begin{aligned} = \left[ 0.1926,\,\,0.2442,\,0.2757,\,0.0035,\,\,0.0234,\,\,0.0359 \right] \end{aligned}$$The valid values can be limited by polygon \((AA'C'BC)\) where \(A (0, a1, 0); A'(a1', 0, 0); B'(b1', b1, 1); \) \(C(0, c1, 0); C'(c1', 0, 0); B(b1', b1, 0)\) Rule 2: includes 6 parameters a, b, c and \(a', b', c'\) where a, b, c are corresponding to the second triangle of real part and \(a', b', c'\) are corresponding to the second triangle of imaginary part.
$$\begin{aligned} (a,\,b,\,c,\,{a}',\,{b}',\,{c}')=\left[ {{a}_{2}},\,{{b}_{2}},{{c}_{2}},{{{{a}'}}_{2}},{{{{b}'}}_{2}},{{{{c}'}}_{2}} \right] \end{aligned}$$$$\begin{aligned} =\left[ 0.1636,\,\,0.1808,\,0.2089,\,\,0.0032,\,0.0152,\,0.0266 \right] \end{aligned}$$The valid values can be limited by polygon \((AA'C'BC)\) where \(A (0, a2, 0); A'(a2', 0, 0); B'(b2', b2, 1);\) \( C(0, c2, 0); C'(c2', 0, 0); B(b2', b2, 0)\)
-
4.
Step 4: Calculate the degree of membership of input data \(X_2'\) Input data \(X_2'\) \(X_2'\):x[(0.1412, 0.0157), (0.1647, 0.0039), (0.1686, 0.0275), (0.2275, 0.0392), (0.2314, 0.0196), (0.3294, 0.0275), (0.2157, 0.0392), (0.2118, 0.0392), (0.1608, 0.0392)]
-
1.
Step 4.1: Calculate invalid value (outbound value)
-
The polygon \(AA'C'BC\) is formed as in Fig. 14. There are two outbound regions. The first one is formed by polygon \(OAA'\); the other one is formed by the region out of polygon \(OAA'C'BC\).
-
The invalid value in out bound region will be updated by the parameter \(\delta \). In which, \(\delta \) is determined step by step as below:
-
Step 1: Find invalid values have axis-x or axis-y \(< 0\) and convert satisfied all of the invalid values have axis-x and axis-y \(\ge 0\).
-
Step 2: Determine \(\delta \) with invalid value: \(\cdot \) Initial \(a = 1, b = 255\) \(\cdot \) Calculate \(\delta =\frac{a+b}{2}\) \(\cdot \) Divide all invalid values to \(\delta \). If at least one invalid value is outbound, we update \(a=\delta \). Otherwise, if all invalid values are inbound, we update \(b=\delta \). \(\cdot \) Repeat until the difference between two consecutive values of \(\delta \) is less than or equal the threshold \(\varepsilon \).
-
Step 3: Update invalid value In the region \(OAA'\), we multiply each invalid value with \(\delta \) In the region out of polygon \(OAA'C'BC\), we divide each invalid value for \(\delta \) or \(-\delta \) satisfied each new value of axis-x and axis-y \(> 0\).
-
-
2.
Step 4.2: Determine the degree of membership - The first input (0.1412, 0.0157) and Rule 1 + Define point D have corresponded \((0.1412, 0.0157, 0)\), D is the correspond of input in polygon \(AA'C'BC\) + E is the intersection of BD and \(A'C'\) + Define point F satisfied \(F \subset (A'B'C')\) and DF is perpendicular with \(AA'C'BC\). So the height DF will be the degree of membership U of input (0.1412, 0.0157). \(\frac{DF}{B{B}'}=\frac{DE}{BE}\) \(\Rightarrow \) \(DF=\frac{B{B}'*DE}{BE}=\frac{1*0.1416}{0.2449}=0.5782\) - The first input (0.1412, 0.0157) and Rule 2 + Define point D have corresponded \((0.1412, 0.0157, 0)\), D is the correspond of input in polygon \(AA'C'BC\) + E is the intersection of BD and \(A'C'\) + Define point F satisfied \(F \subset (A'B'C')\) and DF is perpendicular with \(AA'C'BC\). So the height DF will be the degree of membership U of input (0.1412, 0.0157). \(\frac{DF}{B{B}'}=\frac{DE}{BE}\) \(\Rightarrow \) \(DF=\,\frac{B{B}'\times DE}{BE}=\frac{1 \times 0.1412}{0.1808}=0.7810\) Similiarly with the other point. - The second input (0.1647, 0.0039) + Rule 1: DF = 0.1584 + Rule 2: DF = 0.251 - The third input (0.1686, 0.0275) + Rule 1: Because this value is invalid (outbound), we divide it to \(\delta \) = 3; DF = 0. 0.2303 + Rule 2: Because this value is invalid (outbound), we divide it to \(\delta \) = 3; DF = 0.311 - The \(four^{th}\) input (0.2275, 0.0392) + Rule 1: Because this value is invalid (outbound), we divide it to \(\delta \) = 3; DF = 0.3106 + Rule 2: Because this value is invalid (outbound), we divide it to \(\delta \) = 3; DF = 0.4192 - The \(fif^{th}\) input (0.2314, 0.0196) + Rule 1: DF = 0.8337 + Rule 2: Because this value is invalid (outbound), we divide it to \(\delta \) = 3; DF = 0.3117 - The \(six^{th}\) input (0.3294, 0.0275) + Rule 1: Because this value is invalid (outbound), we divide it to \(\delta \) = 3; DF = 0.3149 + Rule 2: Because this value is invalid (outbound), we divide it to \(\delta \) = 3; DF = 0.5221 - The \(seven^{th}\) input (0.2157, 0.0392) + Rule 1: Because this value is invalid (outbound), we divide it to \(\delta \) = 3; DF = 0.2944 + Rule 2: Because this value is invalid (outbound), we divide it to \(\delta \) = 3; DF = 0.3977 - The \(eigh^{th}\) input (0.2118, 0.0392) + Rule 1: Because this value is invalid (outbound), we divide it to \(\delta \) = 3; DF = 0.289 + Rule 2: Because this value is invalid (outbound), we divide it to \(\delta \) = 3; DF = 0.3905 - The \(nin^{th}\) input (0.1608, 0.0392) + Rule 1: Because this value is invalid (outbound), we divide it to \(\delta \) = 3; DF = 0.2195 + Rule 2: Because this value is invalid (outbound), we divide it to \(\delta \) = 3; DF = 0.2965
-
1.
-
3.
Step 5: Determine defuzzification value (DEF) Initial parameter \((h1, h2, h3, h1', h2', h3') = (1, 2, 1, 1, 2, 1)\) and using the defuzzification formulas (24) and (25), we obtain DEF of Rule 1: \(DEF(X_1)= 0.2101;DEF(HoD_1)=0.0083\); DEF of Rule 2: \(DEF(X_1)= 0.0918;DEF(HoD_1)=0.006\); Using Adam Stochastic Optimization algorithm (2) o find optimize value of parameter. After training, we take \((h1, h2, h3, h1', h2', h3') = (1, 0.7, 0.7, 1, 0.7, 0.7)\)
-
4.
Step 6: Predict output image
-
(a)
Step 6.1: Determine \(O^*_{i.Rel}\) and \(O_{i.Img}^{*}\) In step 5.2 we have MIN of \(U_{A_{_{kj}}}\) \(= MIN (DF \) of rule 1, DF of rule 2) = \(MIN (0.5782, 0.7810) = 0.5782\). Similarly, with the other ones of input data X. We take the degree of membership value U We used two formulae above (22), (23) to determine \(O^*_{i.Rel}\) and \(O_{i.Img}^{*}\).
$$O{{_{i}^{*}}^{ }}=(O_{i.\operatorname {Re}l}^{*},\,O_{i.\operatorname {Im}g}^{*})= \left[ \begin{array}{*{35}{r}} 0.175802 & 0.009461 \\ 0.169767 & 0.009338 \\ 0.175812 & 0.009461 \\ 0.175833 & 0.009462 \\ 0.22323 & 0.010429 \\ 0.168092 & 0.009304 \\ 0.175798 & 0.009461 \\ 0.175789 & 0.009461 \\ 0.175801 & 0.009461 \\ \end{array} \right] $$ -
(b)
Step 6.2: Determine the final prediction result The output pixel values of the predicted image are determined directly from the real part result \(O_{i.Rel}\) (computed in step 4.2), while the imaginary part is computed based on the phase variation ratio of \(O'_{i.Img}\) as given by (27). In this equation, \(X_{i}^{t-1}\) represents the ground truth value at time step \(t-1\).
$$O_{i.\operatorname {Im}g}^{{{*}'}}=\,{{X}_{i}}^{(t-1)}*(1+O_{i.\operatorname {Im}g}^{*})=\left[ \begin{array}{*{35}{r}} 0.142536 \\ 0.186021 \\ 0.166258 \\ 0.189981 \\ 0.26544 \\ 0.2929 \\ 0.217741 \\ 0.205829 \\ 0.182107 \\ \end{array} \right] $$Finally, the final prediction output is calculated by both real and imaginary parts according to formula (28). To get the best result, we used Adam optimization algorithm again to find the optimize parameter \(\gamma \). After training we have \(\gamma = 0.00001\) The predicted image of \(X_3^*\) as follows:
$$X_{3}^{*}=\left[ \begin{array}{*{35}{r}} 0.1425 \\ 0.186 \\ 0.1663 \\ 0.19 \\ 0.2654 \\ 0.2929 \\ 0.2177 \\ 0.2058 \\ 0.1821 \\ \end{array} \right] $$ -
(c)
Step 6.3: Convert to original space and denoising Converting the predicted image of \(X_3^*\) to the original domain and denoising it results in:
$$X_{3}^{*}=\left[ \begin{array}{*{35}{r}} 36 \\ 47 \\ 42 \\ 48 \\ 68 \\ 75 \\ 56 \\ 52 \\ 46 \\ \end{array} \right] $$Prediction output Image (Fig. 17):
-
(a)
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Thang, N.T., Giang, L.T., Son, L.H. et al. A novel spatial complex fuzzy inference system for detection of changes in remote sensing images. Appl Intell 55, 178 (2025). https://doi.org/10.1007/s10489-024-06000-0
Accepted:
Published:
DOI: https://doi.org/10.1007/s10489-024-06000-0