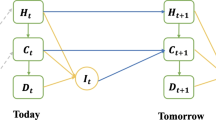
Abstract
Causal effects estimation is essential for analyzing the causal effects of treatment (intervention) on outcome, but traditional methods often rely on the strong assumption of no unobserved confounding factors. We propose ECEE-RL (Enhanced Causal Effects Estimation based on Reinforcement Learning), a novel architecture that leverages offline reinforcement learning to relax this assumption. ECEE-RL innovatively models causal effects estimation as a stateless Markov Decision Process, allowing for adaptive policy optimization through action-reward combinations. By framing estimation as "actions" and sensitivity analysis results as "rewards", ECEE-RL minimizes sensitivity to confounders, including unobserved ones. Theoretical analysis confirms the convergence and robustness of ECEE-RL. Experiments on the two simulated datasets demonstrate significant improvements, with CATE MSE reductions ranging from 5.45% to 66.55% and sensitivity significance reductions of up to 98.29% compared to baseline methods. These results corroborate our theoretical findings on ECEE-RL's improved accuracy and robustness. Application to real-world pilot-aircraft interaction data reveals significant causal effects of control behaviors on bioelectrical signals and emotions, demonstrating ECEE-RL's practical utility. While computationally intensive, ECEE-RL offers a promising approach for causal effects estimation, particularly in scenarios where unobserved confounding may be present, representing an important step towards more reliable causal inference in complex real-world settings.




















Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Data availability
This study utilizes two simulated datasets to support its findings: the IBM Causal Inference Benchmarking Framework, openly available at https://github.com/IBM-HRL-MLHLS/IBM-Causal-Inference-Benchmarking-Framework, and the Infant Health and Development Program (IHDP) dataset, available at https://raw.githubusercontent.com/AMLab-Amsterdam/CEVAE/master/datasets/IHDP/csv/ihdp_npci_1.csv.
The real dataset used to support the findings of this study are available from the corresponding author upon request.
References
Bollen KA (1989) Structural equations with latent variables. John Wiley & Sons, New York, pp 80–134
Pearl J (2009) Causal inference in statistics: An overview. Stat Surv 3:96–146
Peters J, Janzing D, Schölkopf B (2017) Elements of causal inference: foundations and learning algorithms. MIT Press, Cambridge, pp 45–89
Rubin Donald B (1974) Estimating causal effects of treatments in randomized and nonrandomized studies. J Educ Psychol 66(5):688
Mackey L, Syrgkanis V, Zadik I (2018) Orthogonal machine learning: Power and limitations. In: Proceedings of the 35th International Conference on Machine Learning, PMLR 80:3375–3383
Nie X, Wager S (2021) Quasi-oracle estimation of heterogeneous treatment effects. Biometrika 108(2):299–319
Künzel Sören R et al (2019) Metalearners for estimating heterogeneous treatment effects using machine learning. Proc Natl Acad Sci 116(10):4156–4165
Athey S, Tibshirani J, Wager S (2019) Generalized random forests. Ann Stat 47(2):1148–1178
Oprescu M, Syrgkanis V, Wu ZS (2019) Orthogonal random forest for causal inference. In: Proceedings of the 36th International Conference on Machine Learning, PMLR 97:4932–4941
Wagner CH (1982) Simpson’s paradox in real life. Am Stat 36(1):46–48
Oster E (2019) Unobservable selection and coefficient stability: Theory and evidence. J Bus Econ Stat 37(2):187–204
Prudencio RF, Maximo MROA, Colombini EL (2023) A survey on offline reinforcement learning: Taxonomy, review, and open problems. IEEE Trans Neural Netw Learn Syst 34(9):6032–6051
Szepesvári C (2022) Algorithms for reinforcement learning. Synthesis Lectures on Artificial Intelligence and Machine Learning, Morgan & Claypool Publishers 16(1):23–47
Jung Y, Tian J, Bareinboim E (2020) Estimating causal effects using weighting-based estimators. Proc AAAI Conf Artif Intell 34(06):10186–10193
Kallus N (2020) Generalized optimal matching methods for causal inference. J Mach Learn Res 21(62):1–54
Hünermund P, Louw B, Caspi I (2023) Double machine learning and automated confounder selection: A cautionary tale. J Causal Infer 11(1):20220078
Sant’Anna PHC, Zhao J (2020) Doubly robust difference-in-differences estimators. J Econom 219(1):101–122
Tang C, Wang H, Li X et al (2022) Debiased causal tree: Heterogeneous treatment effects estimation with unmeasured confounding. Adv Neural Inf Process Syst 35:5628–5640
Friedberg R, Tibshirani J, Athey S et al (2020) Local linear forests. J Comput Graph Stat 30(2):503–517
Scanagatta M, Salmerón A, Stella F (2019) A survey on Bayesian network structure learning from data. Prog Artif Intell 8(4):425–439
Bellemare MF, Bloem JR, Wexler N (2020) The Paper of How: Estimating Treatment Effects Using the Front-Door Criterion. Oxf Bull Econ Stat 86(4):951–993
Pearl J, Bareinboim E (2022) External validity: From do-calculus to transportability across populations. In: Probabilistic Causal Inference: The Works of Judea Pearl, World Scientific, Singapore, pp 451–482
Tudball MJ (2023) Sensitivity analyses for causal inference. PhD Thesis, University of Bristol, Bristol, pp 67–92
Eggers AC, Tuñón G, Dafoe A (2023) Placebo tests for causal inference. Am J Pol Sci 68(3):1106–1121
Ding P (2022) Sensitivity analysis without an identifying assumption. Ann Stat 50(5):2524–2548
Cinelli C et al (2020) Making Sense of Sensitivity: Extending Omitted Variable Bias. J Royal Stat Soc: Ser B (Stat Methodol) 82(1):39–67
Fogarty CB et al (2021) Discrete Optimization for Causal Inference: Strengths, Limitations, and Guidelines for Application. arXiv preprint arXiv:2106.11989
Hazlett C (2021) Kernel balancing: A flexible non-parametric reweighting procedure for causal inference. Am Stat 75(2):137–148
Andrews I et al (2017) A simple algorithm for robust regression with dependent data. arXiv preprint arXiv:1703.08906
Huber M, Chen B, Richardson T, Drton M (2019) Probabilistic integration of causal knowledge and uncertain associations. In: Proceedings of the 35th Conference on Uncertainty in Artificial Intelligence, Tel Aviv, Israel. AUAI Press, pp 385–394
Jang B, Kim M, Harerimana G et al (2019) Q-learning algorithms: A comprehensive classification and applications. IEEE Access 7:133653–133667
Zhang Y, Zhao B, Liu D (2020) Deterministic policy gradient adaptive dynamic programming for model-free optimal control. Neurocomputing 387:40–50
Qiu C, Hu Y, Chen Y et al (2019) Deep deterministic policy gradient (DDPG)-based energy harvesting wireless communications. IEEE Internet Things J 6(5):8577–8588
Haarnoja T, Zhou A, Abbeel P, Levine S (2018) Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor. In: Proceedings of the 35th International Conference on Machine Learning, Stockholm, PMLR 80:1861–1870
Wang L, Yang Z, Wang Z (2021) Provably efficient causal reinforcement learning with confounded observational data. Adv Neural Inf Process Syst 34:21164–21175
Gasse M, Grasset D, Gaudron G, et al (2021) Causal reinforcement learning using observational and interventional data. arXiv preprint arXiv:2106.14421, pp 4–9
Zhu S, Ng I, Chen Z (2020) Causal discovery with reinforcement learning. In: International Conference on Learning Representations, Virtual Conference, pp 3–8
He X, Yang H, Hu Z, Lv C (2023) Robust Lane Change Decision Making for Autonomous Vehicles: An Observation Adversarial Reinforcement Learning Approach. IEEE Trans Intell Veh 8(1):184–193
Shi C et al (2023) (2023) Dynamic causal effects evaluation in a/b testing with a reinforcement learning framework. J Am Stat Assoc 118(543):2059–2071
Zhu Y, Hubbard RA, Chubak J et al (2021) Core concepts in pharmacoepidemiology: Violations of the positivity assumption in the causal analysis of observational data: Consequences and statistical approaches. Pharmacoepidemiol Drug Saf 30(11):1471–1485
Sajons GB (2020) Estimating the causal effect of measured endogenous variables: A tutorial on experimentally randomized instrumental variables. Leadersh Q 31(5):101348
Xing Y, Duan Q, Zhang G, Chen L (2021) Differential evolution algorithm based on entropy weight method to determine the weight to optimize the configuration of wind, solar, and diesel microgrid. J Phys: Conf Ser 1871(1):012034
Rosenman R, van der Laan B, Hubbard J (2019) Generating random confounding for robust causal inference. J Causal Inference 7(1):1–15
Takuma S, Imai M (2022) [Source code]. https://github.com/takuseno/d3rlpy
Amit S, Kiciman E et al (2019) [Source code]. https://github.com/py-why/dowhy
Shimoni Y, Yanover C, Karavani E, et al (2018) Benchmarking framework for performance-evaluation of causal inference analysis. arXiv preprint arXiv:1802.05046
MacDorman MF, Atkinson JO (1998) Infant mortality statistics from the linked birth/infant death data set - 1995 period data. Mon Vital Stat Rep 46(6):1–22
Kennedy EH (2023) Towards optimal doubly robust estimation of heterogeneous causal effects. Electron J Stat 17(2):3008–3049
Cheng D, Li J, Liu L, Le Jixue Liu T (2020) Local Search for Efficient causal effects estimation. IEEE Trans Knowl Data Eng 35:8823–8837
Aragam B, Zhou Q (2015) Concave penalized estimation of sparse Gaussian Bayesian networks. J Mach Learn Res 16:2273–2328
Acknowledgements
This research was supported by the National Natural Science Foundation of China (Grant No. 62106269).
Author information
Authors and Affiliations
Contributions
Huan Xia: Conceptualization, Formal analysis, Methodology, Software, Validation, Visualization, Writing; Chaozhe Jiang: Project administration, Supervision, Resources; Chenyang Zhang: Investigation, Data curation.
Corresponding author
Ethics declarations
Competing interest
The authors declare that they have no conflicts of interest.
Ethical and informed consent for data used
The dataset used in this study includes publicly available IBM Causal Inference Benchmarking Dataset, IHDP Dataset and real pilot operation data. For public datasets, we follow their open license agreement. As for the real operation dataset of pilots, it includes biological measurement data such as control inputs, facial features, and EEG of pilots on the simulator. The collection and use of this dataset were conducted with the informed consent of all relevant pilots, which is in compliance with the ethical requirements of biological behavior research. All pilot identity information has been de identified in the dataset. We promise to use the dataset only for academic analysis and research, and not for any commercial purposes. We will take measures to protect the privacy of pilots.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Xia, H., Jiang, C. & Zhang, C. Enhanced causal effects estimation based on offline reinforcement learning. Appl Intell 55, 278 (2025). https://doi.org/10.1007/s10489-024-06009-5
Accepted:
Published:
DOI: https://doi.org/10.1007/s10489-024-06009-5